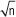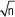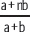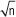c) En una competencia entre cuatro personas acordaron repartirse como premio $ 240.000, de manera que el primer lugar se lleva el triple del premio del segundo lugar, lo que se extiende al tercer y cuarto lugar. Determinar los premios correspondientes a cada lugar.

d) En una población de 10.000 conejos se detectó una epidemia que los está exterminando a razón de 10.000 • 2–t, donde t es el tiempo expresado en días. Después de 3 días, ¿cuántos conejos quedan?

6. Determina, en cada caso, si la afirmación es verdadera o falsa. Justifica tu respuesta.

a) El cuadrado de un número racional negativo es positivo.

b) El cubo de un número racional negativo es positivo.

c) El producto de potencias de igual base es una potencia cuya base es la misma y cuyo exponente es el producto de los exponentes.

d) Al elevar una fracción a la cuarta, se elevan el numerador y el denominador.

7. Completa cada

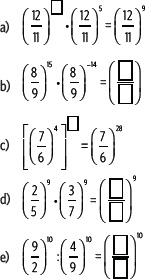
teniendo en cuenta las propiedades de las potencias.

8. Resuelve.

En una fábrica de pasteles se empacan los pasteles en cajas cúbicas cuyas aristas miden 9,5 cm. 9,5 cm

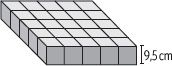
a) ¿Cuál es el volumen de las cajas para empacar pasteles individualmente?

b) Si se empacan los pasteles en grupos de 25 cajas como la de la figura, ¿cuál será el volumen de cada grupo de cajas?

3.3 Notación científica

Definición

La notación científica se utiliza para representar un número racional como el producto entre un número cuyo valor absoluto sea mayor o igual a 1 y menor que 10 y una potencia de 10.

Cuando se multiplica un número decimal por una potencia de 10 con exponente positivo, la coma del número decimal se desplaza tantas cifras a la derecha como lo indique el exponente. Si el exponente de la potencia es negativo, el desplazamiento es a la izquierda. Por ejemplo, –3,756 • 107 = –37.560.000 y 5,922 • 10–4 = 0,0005922.

Actividades resueltas

1. Escribe en notación científica las siguientes medidas.

a) La masa de la Tierra es 5.976.300.000.000.000.000.000.000 kg. 5.976.300.000.000.000.000.000.000 kg = 5,9763 • 1024 kg.

b) La masa del átomo de hidrógeno es 0,00000000000000000000000000167 kg. 0,00000000000000000000000000167 kg = 1,67 • 10–27 kg.

2. Utilizando notación científica, resuelve los siguientes problemas.

a) En un día hay 86.400 segundos. ¿Cuántos segundos hay en 1 año (365 días)?

Segundos en un día: 86.400 = 8,64 • 104

Días en un año: 365 = 3,65 • 102

Se calcula el producto de los segundos en un día por la cantidad de días de un año, esto es, (8,64 • 104) • (3,65 • 102):

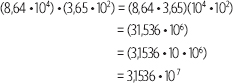
En un año hay 3,1536 • 107 segundos.

b) En su órbita alrededor del Sol, la Tierra recorre cerca de 2.573.000 km cada día. ¿Con qué rapidez, en kilómetros por segundos, gira la Tierra en torno al Sol?

Por lo tanto, la Tierra gira alrededor del Sol con una rapidez aproximada de 2,98 • 101 km/s.

En ocasiones se utiliza el “peso” y la “masa” como términos equivalentes. Sin embargo no lo son, ya que el “peso” es una magnitud vectorial y la “masa” un escalar.

Actividades

1. Determina cuáles de los siguientes números están escritos en notación científica.

a) 12,5

b) 1,11 • 10

c) 6,05 • 108

d) 3,64 • 1029

e) 10,9 • 104

f) 0,008 • 1023

g) 2,58 • 1023

h) 0,154 • 106

2. Escribe los siguientes números en notación científica.

a) 2.200

b) 56.040.000

c) 0,0015

d) 0,00000036

e) 3.520.000

f) 345,876

3. Escribe los siguientes números en notación decimal.

a) 6,8 • 1024

b) 6,72 • 105

c) 2,115 • 104

d) 5,31 • 1025

e) 5,04 • 102

f) 7,31 • 1025

4. Escribe las siguientes magnitudes usando la notación científica.

a) Una tonelada métrica equivale a 1.000.000 g.

b) Un nanómetro es una unidad de medida que se utiliza para medir la radiación ultravioleta y equivale a 0,000000001 metros.

c) El área de la superficie de Australia es aproximadamente 7.686.850.000.000 m2.

d) El número aproximado de átomos en 1 gramo de oro es 278.000.000.000.000.000.000.

e) La precisión de una balanza es 0,00000001 g.

f) El número de Avogadro (número de partículas en una molécula-gramo o mol) es 602.200.000.000.000.000.000.000.

g) La luz recorre 1 metro en aproximadamente 0,000000003 segundos.

5. Calcula y expresa tu respuesta en notación científica.

6. Utilizando notación científica, resuelve los siguientes problemas.

a) El Pioner II voló alrededor de Júpiter con una rapidez cercana a 173.000 km/h. ¿A cuántos kilómetros por segundos viajó?

b) Cierto isótopo tiene una vida media de 1,65 • 10–4 segundos. Mientras que otro tiene una vida media de 1,64 • 10–4 segundos. ¿Cuántas veces más larga es la vida media del primer isótopo respecto del segundo?

7. En el análisis de una muestra de sangre de un paciente se encontró que el número de glóbulos rojos por mm3 de sangre es 4,8 • 106. Utilizando notación científica resuelve.

a) ¿Cuál es el número de glóbulos rojos de este paciente si su cuerpo contiene aproximadamente 5 litros de sangre?

b) Si el diámetro de un glóbulo rojo es aproximadamente 10–2 mm, ¿cuál es la longitud en kilómetros de una hilera formada por los glóbulos rojos de este paciente?

c) Si la longitud del ecuador es aproximadamente de 40.000 km, ¿cuántas veces podría dar la vuelta a la Tierra esta hilera de glóbulos rojos?

3.4 Raíces

Raíz enésima

Propiedades de las raíces

Es importante tener en cuenta que para los exponentes racionales también se cumplen las propiedades de las potencias, y que de estas se pueden deducir las siguientes propiedades para raíces enésimas:

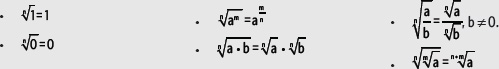
Actividades resueltas

1. Escribe la expresión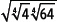

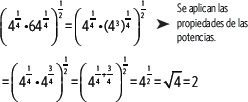
como potencia y calcula su resultado.

2. Escribe la expresión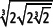

como una potencia de exponente racional.

3. Aplica las propiedades de las raíces para simplificar la siguiente expresión algebraica.

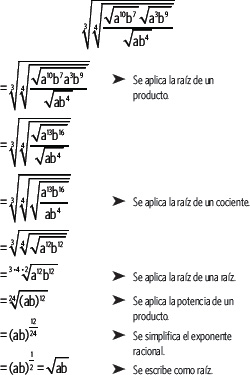
Actividades

1. Completa la tabla.

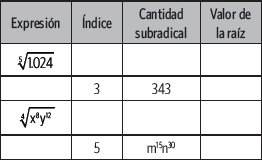
2. Explica cuál es el error en el siguiente procedimiento.

3. Numera los pasos para simplificar la siguiente expresión.

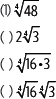
4. Aplica las propiedades de las raíces para simplificar las siguientes expresiones.

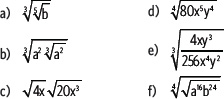
5. Calcula el valor de m en cada caso.

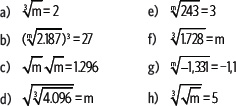
6. Escribe las expresiones como potencias de exponente racional. Luego, simplifica si es posible,

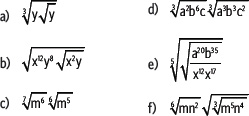
7. Completa cada una de las siguientes igualdades.

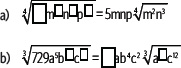
8. Lee y resuelve.

Según la teoría de la relatividad de Einstein, la masa m de un objeto que se mueve a una velocidad v está dada por:

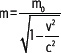
Donde m0 es la masa del objeto en reposo y c = 3 • 108 m/s.

Calcula la masa de un protón que se desplaza con v = 0,5c si su masa en reposo es 1,6 • 10–27 kg.

9. Un cono es un cuerpo de revolución generado por un triángulo rectángulo que gira sobre uno de sus catetos. El cateto sobre el que gira es la altura y la hipotenusa es la generatriz del cono.

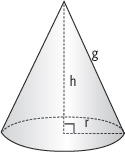
Determina la generatriz g del cono si:

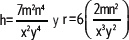
3.5 Operaciones con raíces

Adición y sustracción de raíces

Para resolver adiciones o sustracciones con raíces es posible realizar un procedimiento similar a la operatoria con términos semejantes.

Actividad resuelta

y h = b – c + a, ¿cuál es el valor de h?

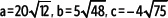
Por lo tanto, el valor de h es

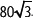
Multiplicación y división de raíces

Para multiplicar y dividir raíces se pueden considerar los siguientes casos:

Con igual índice Con distinto índice Multiplicación: se multiplican tanto los coeficientes como las cantidades subradicales entre sí y se aplica la propiedad de la raíz de un producto. Luego, se simplifica el resultado.

División: se dividen los coeficientes entre sí y las cantidades subradicales se escriben dentro del mismo radical. Se simplifican hasta donde sea posible. Cuando se multiplican o dividen raíces con distinto índice se transforman a raíces con igual índice y se procede como en el caso anterior. Para determinar el índice común: • se calcula el mínimo común múltiplo entre los índices de las raíces, el cual será el índice común. • se divide el índice común por el índice de la raíz y se eleva la cantidad subradical a ese resultado.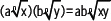

Actividad resuelta

Calcula el siguiente producto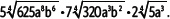

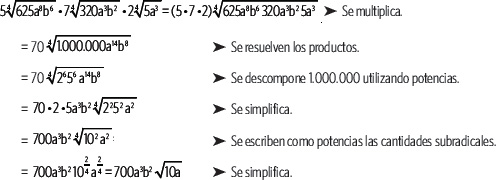
Actividades

1. Resuelve las siguientes operaciones.

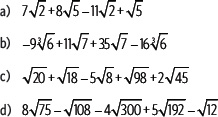
2. Determina los números que hacen verdadera cada igualdad.

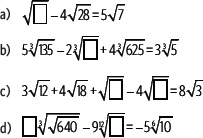
3. Calcula el producto en cada caso. Simplifica el resultado.

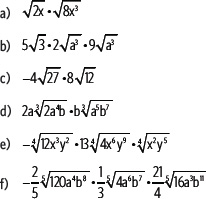
4. Ordena cada grupo de números de mayor a menor.

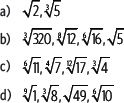
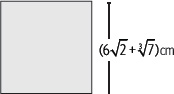
5. Deduce una expresión algebraica para expresar el área del cuadrado.

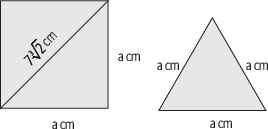
6. Determina el área de un triángulo equilátero cuyo lado tiene la misma medida que el lado de un cuadrado, como se muestra en la figura.

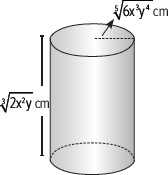
7. Determina la expresión del volumen del siguiente cuerpo.

8. Calcula el valor de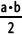

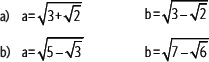
si:

9. Demuestra que:

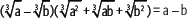
10. Determina el valor de k

para que se cumpla la igualdad.

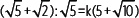
3.6 Racionalización

Cuando una fracción tiene raíces en el denominador es posible encontrar una expresión equivalente sin raíces en el denominador por medio de la racionalización. Para ello se amplifica por una expresión adecuada, de forma que permita expresar el denominador sin raíces.

Actividad resuelta

Racionaliza las expresiones

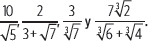
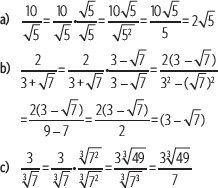
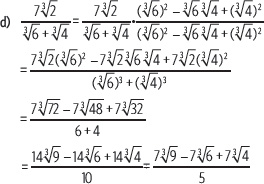
Actividades

1. En cada caso, multiplica por una expresión que permita simplificar las raíces. Justifica tu respuesta.

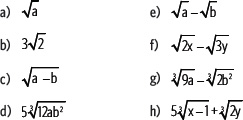
2. Enumera los pasos para racionalizar la expresión.

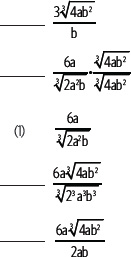
3. Racionaliza las siguientes expresiones.

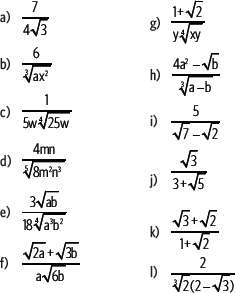
4. En el movimiento de un péndulo, el período T está determinado por la expresión.

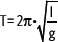
l: longitud y g: gravedad.

a) Racionaliza la expresión asociada al período de un péndulo.

b) Calcula el período si l =

m, considerando g = 9,8 m/s2.

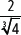
5. La velocidad del agua en canales abiertos está determinada por la fórmula de Manning.

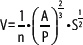
a) Escribe en forma de radical la expresión de la velocidad del agua.

b) Racionaliza la fórmula de Manning.

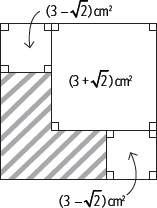
6. Determina el orden de menor a mayor entre los siguientes números.

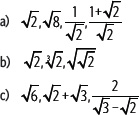
7. La siguiente figura está formada por un cuadrado dentro del cual se dibujaron otros tres cuadrados cuyas áreas se especifican en las figuras. Determina el área de la figura pintada.

3.7 Aproximación en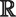

Dado que un número irracional tiene infinitas cifras decimales no periódicas, no es posible tener una representación exacta de la cantidad de cifras decimales que tiene. Es por ello que se pueden aproximar por truncamiento y por redondeo.

Aproximación por truncamiento

Para truncar un número en cierta cifra decimal, se eliminan las cifras decimales que le siguen.

Actividad resuelta

Aproxima truncando a la milésima el número irracional 3,141516171819...

Al truncarlo a la milésima se obtiene: 3,141.

Aproximación por redondeo

Para redondear un número en una cierta cifra decimal hay que fijarse en el valor de la cifra siguiente; si es mayor o igual a 5, se suma 1 a la cifra por redondear y las restantes no se consideran. Si la cifra es menor que 5, se mantiene igual y las restantes cifras decimales no se consideran.

Actividad resuelta

Aproxima redondeando a la milésima el número irracional 3,141516171819...

Al redondearlo a la milésima se obtiene 3,142.

Algunos tipos de aproximaciones para números correspondientes a raíces cuadradas no exactas son la aproximación pitagórica y la aproximación por acotación sucesiva.

Aproximación pitagórica