
Полная версия
Manual de preparación PSU Matemática
Actividad resuelta
Si z1 = –3 – 5i, z2 = 2 + 3i, verifica que se cumple la propiedad conmutativa.
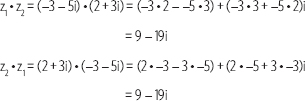
Actividades
1. Si z1 = 3 – 5i, z2 = 4 – 2i, z3 = 3 + 5i, z4 = –6 – 8i calcula:
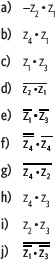
2. Demuestra las siguientes propiedades. Considera z1, z2 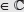

3. Completa la siguiente tabla teniendo en cuenta que:
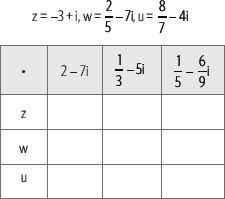
4. Calcula cada producto y luego represéntalo en el plano de Argand.
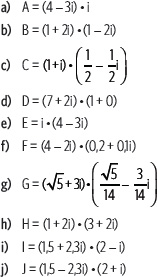
5. Calcula el inverso multiplicativo de los siguientes números complejos.
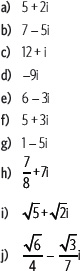
4.7 División en

Para resolver una división entre z1 = a + bi, z2 = c + di es posible amplificar por el conjugado del denominador y determinar el resultado:
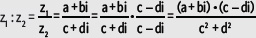
De manera equivalente:
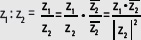
Actividades resueltas
1. Si z1 = –2 + 3i, z2 = 1 + 2i, calcula z1 : z2.
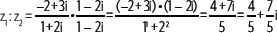
2. La impedancia es un fenómeno físico que se describe por medio de oscilaciones y es de gran importancia en ingeniería electrónica. La impedancia Z (en ohms) afecta la corriente en un circuito y se determina mediante la fórmula: 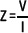
Resolución:

Respuesta: La impedancia es (2 + 5i) ohms.
3. En la igualdad: z(–5 + 4i) = 4 – 4i, ¿cuál es el valor de z?
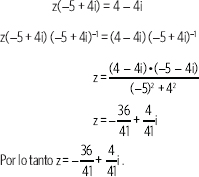
Actividades
1. Resuelve las siguientes divisiones.
a) (3 – 2i) : (5 + 3i)
b) 9i : (4 – i)
c) (1 + i) : (–1 – i)
d) (5 + 2i) : (7 + i)
e) (12 – 2i) : 5i
f) (2 – i) : 8i
g) (4 – 2i) : (1 + 5i)
h) (4 + 2i) : (1 – i)
i) (5 – 5i) : (1 – i)
2. Determina si cada igualdad es verdadera o falsa. Para ello, considera z1 = 3 + 2i, z2 = 2 – i.
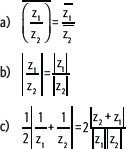
3. Determina el valor de z según corresponda.
a) z(1 + i) = (3 + i)
b) (2 + 2i)z = 5i
c) 9 = z(7 + 2i)
d) (1 – 2i)z = (3 + 2i)
e) 7zi = (8 – i)
f) i = (6 + 8i)z
g) z(3 – i) = (1 + i)
h) (4 – i) = (3 + 5i)z
i) (3 + i)z = (6 + 3i)(–1 + i)
4. Resuelve las siguientes divisiones. Para ello, considera z1 = 4 + 2i, z2 = –1 – i, z3 = 2 – i,
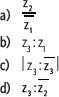
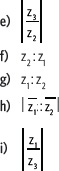
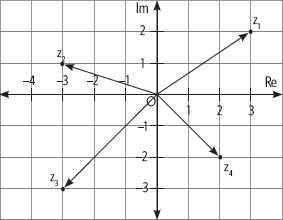
5. En el plano de Argand se han representado los números complejos z1, z2, z3 y z4. Considerando lo anterior, resuelve.
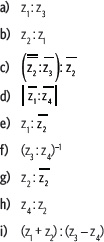
4.8 Potencias de números complejos
Si z
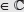
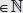
Para exponentes negativos se tiene que z–n =

Se puede calcular la potencia de un número complejo utilizando las expresiones del cuadrado y del cubo de binomio y luego remplazar los valores de las potencias de i cuando corresponda.
Para calcular potencias de mayor grado, se pueden combinar las propiedades de las potencias con cuadrados y cubos de un binomio.
Actividad resuelta
Calcula el valor de la potencia de cada número complejo.

Actividades
1. Calcula el valor de las siguientes potencias.
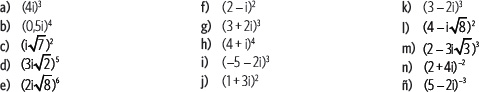
4.9 Raíces cuadradas de números complejos
Se define la raíz cuadrada de un número complejo z como un número complejo w, tal que w2 = z, es decir,
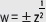
Para determinar las raíces cuadradas de un número complejo z = a + bi, con b ≠ 0, se puede plantear la ecuación a + bi = (x + iy)2, con x e y números reales. Luego, para resolverla se reescribe como un sistema de ecuaciones, esto es, escribiendo una ecuación para igualar las partes reales y otra, para las partes imaginarias. Si en algún caso se obtuviera que x o y no fueran números reales, dicho caso se descarta. A partir de este proceso, se tiene que siempre existe, y corresponde a dos números complejos distintos, que tienen como característica que son inversos aditivos uno del otro.
Actividades resueltas
1. Determina las raíces cuadradas de z = 6i.
Se buscan los números complejos w = x + iy, tales que w2 = z. Es decir:

2. ¿Cuáles son las raíces cuadradas de z = 2i?
Se resuelve la ecuación (x + iy)2 = 2i, luego se tiene:

Actividades
1. Calcula las raíces cuadradas de cada número complejo.
a) z1 = 4i
b) z2 = 3 – 4i
c) z3 = 15 + 8i
4.10 Números complejos en forma polar
Dado un número complejo z = a + bi, representado en el plano de Argand, se tienen las siguientes relaciones:

Actividades resueltas
1. Escribe en forma polar el número complejo z = 1 + i.
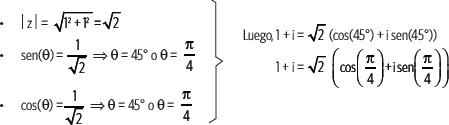
Para profundizar el estudio de las razones trigonométricas puedes revisar el Anexo de Trigonometría (pág. 326).
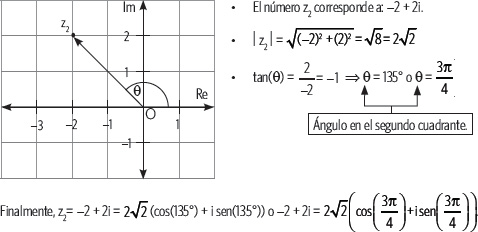
2. ¿Cuál es la forma polar del número complejo z2 representado en el plano de Argand?
Actividades
1. Representa en forma polar los siguientes números complejos.
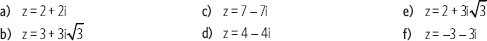
4.11 Potencias y raíces de números complejos en forma polar
Dado un número complejo z = |z| (cos(θ) + i sen(θ)), se tiene que:
• La potencia enésima es: zn = |z|n (cos(n • θ) + i sen(n • θ)), n
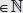
• La raíz enésima es:
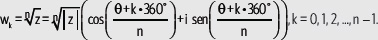
Así, se obtienen n raíces, cuyos ángulos correspondientes tienen una diferencia igual a

Al representarlas en el plano de Argand, se obtienen n puntos sobre una circunferencia con centro en el origen y radio
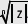
Actividad resuelta
Si la representación en forma polar del número z = –2 + 2i es z = 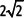
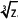
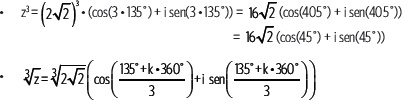
Con los valores de k se obtienen las 3 raíces, que en este caso son w0, w1 y w2.
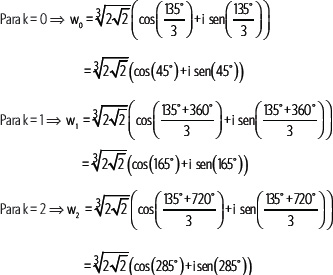
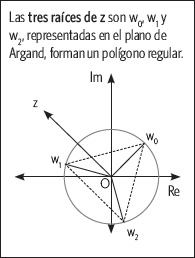
Actividades
1. Calcula lo pedido y luego grafica las raíces en el plano de Argand.

Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.



