Manual de preparación PSU Matemática

b) ¿Qué isla está más alejada de la costa?

c) Organiza, de menor a mayor distancia, las islas teniendo en cuenta la playa.

2.3 Operatoria en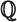

Adición y sustracción de números racionales escritos como fracción

Actividades resueltas

1. Calcula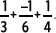

El mínimo común múltiplo entre 3, 6 y 4 es 24. Amplificando cada fracción se obtienen fracciones equivalentes:

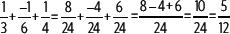
2. Calcula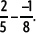

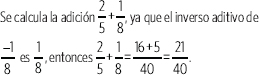
Multiplicación y división de números racionales

Actividades resueltas

1. Calcula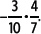

Se multiplican numeradores y denominadores entre sí, teniendo en cuenta los signos de cada número entero, y se simplifica el resultado.

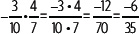
2. Calcula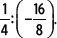

Se multiplica el dividendo por el inverso multiplicativo del divisor, teniendo en cuenta los signos de cada número entero, y se simplifica el resultado.

Propiedades de la adición y de la multiplicación de números racionales

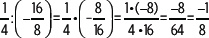
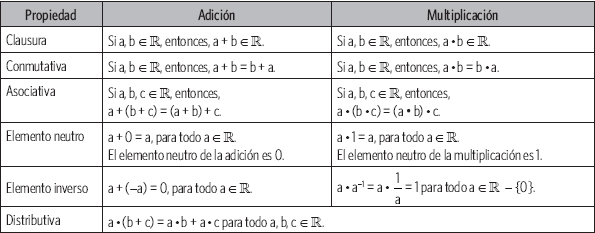
Si a, b, c ∈

, se cumplen las siguientes propiedades:

• Conmutativa de la adición: a + b = b + a

• Asociativa de la adición: a + (b + c) = (a + b) + c

• Conmutativa de la multiplicación: a • b = b • a

• Asociativa de la multiplicación:

a • (b • c) = (a • b) • c

• Distributiva de la multiplicación respecto de la adición:

a • (b + c) = a • b + a • c

Densidad de los números racionales

El conjunto de los números racionales (

) es denso en

. Esto quiere decir que dado un número cualquiera, siempre se puede encontrar un número racional tan cerca de él como se quiera. Por esto, se cumple que dados dos números racionales, se pueden intercalar infinitos números racionales entre ellos.

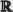
Por ejemplo, dados dos números racionales a y b, se puede intercalar un número racional calculando su promedio

. Otra forma es usar fracciones equivalentes con el mismo denominador y analizar sus numeradores.

Actividad resuelta

Intercala un número racional entre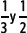

.

1er método

Se calcula el promedio de las fracciones.

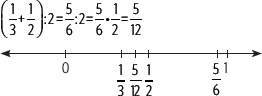
2do método

Se amplifican ambas fracciones para que tengan igual denominador.

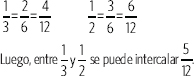
Actividades

1. Resuelve las siguientes adiciones y sustracciones.

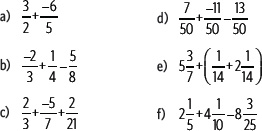
2. Calcula los siguientes productos y cocientes de números racionales.

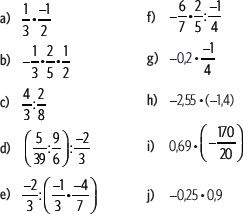
3. Considera los números naturales 3 y 6.

a) Ubica los números en una recta numérica.

b) Calcula el promedio de estos números (puedes usar calculadora) y ubícalo en la recta numérica.

c) ¿Cuál es la distancia que hay entre cada número y el promedio?

d) Intercala un número racional entre cada número y el promedio. ¿Cómo lo hiciste?

4. Ubica en la recta numérica los números –4,2 y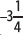

. Luego, intercala un número entre ellos y explica cómo lo hiciste.

5. ¿Cuántos números podrías intercalar entre dos números racionales?, ¿por qué?

6. Para cada par de números racionales ubica tres números decimales entre ellos.

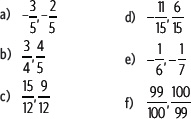
2.4 Operaciones con números decimales

Adición y sustracción de números decimales finitos

Se denomina fracción decimal a aquella cuyo denominador es el valor de una potencia entera de 10. Estas fracciones se pueden representar con números decimales finitos.

Para resolver una adición o una sustracción entre números decimales finitos se pueden alinear los números por la coma decimal y luego sumarlos como números enteros. Se conserva la ubicación de la coma decimal en el resultado obtenido.

Actividad resuelta

Calcula las siguientes operaciones con números decimales.

a) 5,73 + 0,042 + 271,746

Se alinean los sumandos respecto a la coma y se suman como si fueran números enteros.

Por lo tanto, 5,73 + 0,042 + 271,746 = 277,518.

b) 15,73 – 18,042

Para calcular la sustracción, se debe calcular la adición 15,73 + (–18,042).

Se restan los valores absolutos y se mantiene el signo del que tiene mayor valor absoluto.

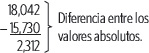
Por lo tanto, 15,73 – 18,042 = –2,312.

Multiplicación y división de números decimales finitos

Para multiplicar números decimales finitos se resuelve como si fueran números enteros y en seguida se separan tantas cifras decimales en el producto como la suma del número de cifras decimales de los factores.

Para dividir números decimales finitos se pueden amplificar los términos de la división por el valor de una potencia de 10, de modo que el divisor sea un número entero.

Cuando los números decimales son infinitos periódicos o semiperiódicos, estos se pueden escribir en su forma fraccionaria y luego resolver las operaciones que correspondan.

Actividad resuelta

Calcula las siguientes operaciones con números decimales.

a) 2,75 • 0,73

b) 2,304 : 0,0096

Actividades

1. Resuelve las siguientes adiciones.

a) 0,030 + 0,5

b) 0,075 + 0,25

c) 0,83 + 0,27

d) 0,45 + 0,187

2. Escribe los números decimales del ejercicio anterior en su forma fraccionaria y resuelve las adiciones correspondientes. Compara los resultados obtenidos.

3. Resuelve las siguientes sustracciones.

a) 0,030 – 0,5

b) 0,075 – 0,25

c) 0,83 – 0,27

d) 0,45 – 0,187

4. Escribe los números decimales del ejercicio anterior en su forma fraccionaria y resuelve las sustracciones correspondientes. Compara los resultados obtenidos.

5. Resuelve las siguientes multiplicaciones.

a) 7,34 • 0,89

b) 2,03 • 0,009

c) 3,75 • 4,01

d) 5,371 • 1,46

6. Resuelve las siguientes divisiones.

a) 0,0017 : 0,034

b) 5,832 : 7,2

c) 0,1331 : 1,21

d) 47,239 : 0,0001

7. Resuelve las siguientes adiciones y sustracciones de números decimales.

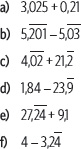
8. Escribe los números decimales del ítem 7 en su forma fraccionaria y realiza las operaciones correspondientes. Luego, compara los resultados.

9. Lee la siguiente información y luego responde.

Una ampolleta se calienta cuando la electricidad pasa a través del filamento. La cantidad de energía eléctrica transformada en energía calórica por el flujo de corriente está dada por la fórmula:

w = R • I2 • t

donde w es la energía calórica medida en joules (J), R es la resistencia del filamento en ohms, I es la corriente en amperes (A) y t es el tiempo en segundos.

a) Calcula el valor de la resistencia de un filamento si la energía calórica obtenida por una corriente eléctrica de 12,456 A durante 15 segundos es 83.771,8097 J.

b) Realiza el cálculo anterior con una calculadora. ¿Obtuviste el mismo resultado?, ¿por qué?

c) ¿Qué aproximación realiza tu calculadora, por redondeo o por truncamiento? Justifica tu respuesta.

3. Números reales (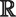

)

3.1 El conjunto de los números reales

Números irracionales (

*)

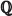
El conjunto de los números irracionales se simboliza como

* y está formado por todos los números que no se pueden escribir de la forma

, con a, b ∈

, b ≠ 0. Por lo tanto, su forma decimal tiene infinitas cifras decimales no periódicas.

Por ejemplo,

, e, π, log 2 son ejemplos de números irracionales ya que en su representación decimal tienen infinitas cifras decimales no periódicas.

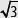
Actividad resuelta

Demuestra que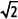

no es un número racional.

Se supone que

es un número racional, con n ≠ 0 y m.c.d.(m, n) = 1.

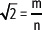
Luego m y n serían números pares, es decir, múltiplos de 2, o bien ambos son divisibles por 2, lo que contradice que m.c.d.(m, n) = 1, es decir, que la fracción sea irreducible.

Por lo tanto, asumir que

es un número racional es incorrecto y se concluye que

es irracional.

Números reales (

)

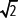
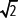
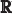
El conjunto de los números reales se simboliza por

.

Propiedades de la adición y de la multiplicación en

Sustracción y división de números reales

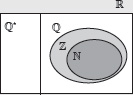
Se pueden expresar las operaciones de sustracción y división en

utilizando el inverso aditivo o el inverso multiplicativo según sea el caso.

Sustracción División a – b = a + (–b), para todo a, b ∈

. a : b = a • b–1, para todo a, b ∈

y b ≠ 0.

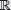
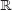
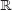
Como el 0 no tiene inverso multiplicativo, la división por cero no está definida.

Actividad resuelta

Realiza las siguientes operaciones.

Actividades

1. Determina si las siguientes afirmaciones son verdaderas o falsas.

a) Un número real puede ser racional e irracional al mismo tiempo.

b) La expresión x ≤ y, con x e y números reales, se puede interpretar como x es menor o igual que y.

2. Demuestra que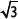

es un número irracional.

3. Determina, en cada caso, si la igualdad es verdadera o falsa. Justifica usando las propiedades de los números reales.

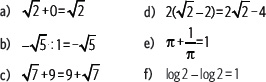
4. Resuelve.

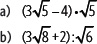
5. Completa la demostración con el nombre de la propiedad que permite realizar cada paso.

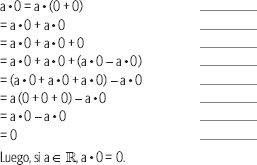
3.2 Potencias y sus propiedades

Definición

Si b ∈

y n ∈

, la potencia bn representa una multiplicación de n factores iguales:

Propiedades de las potencias

A continuación se muestran algunas propiedades de las potencias. Considera n, m ∈

, a, b ∈

– {0}.

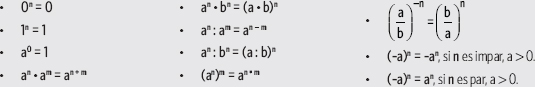
Actividades resueltas

1. Simplifica la siguiente expresión aplicando las propiedades de las potencias.

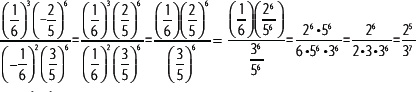
Observación:

En las propiedades de las potencias no se analizan los casos 00 y 0n, con n ∈

.

2. Resuelve el siguiente problema.

Don Mario decide repartir sus 217 ovejas entre sus 5 hijos. El hijo mayor recibirá el doble de animales que el segundo hijo, quien recibirá el doble que el tercer hijo y así sucesivamente. ¿Cuántas ovejas tendrá cada uno?

Resolución:

Si el hijo mayor recibe x ovejas, el segundo hijo recibe la mitad, o sea,

.

El tercer hijo recibe la mitad del segundo, o sea,

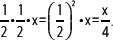
El cuarto hijo recibe la mitad del tercero, o sea,

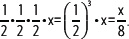
El quinto hijo recibe la mitad del cuarto hijo,

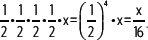
Se resuelve la ecuación:

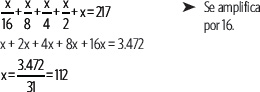
Respuesta: El hijo mayor recibe 112 ovejas; el segundo, 56; el tercero, 28; el cuarto, 14; y el quinto, 7.

Actividades

1. Escribe cada potencia como potencia con exponente positivo.

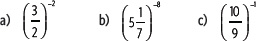
2. Calcula.

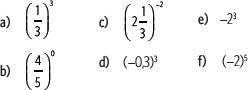
3. Utiliza las propiedades de las potencias para reducir cada expresión.

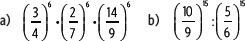
4. Remplaza en cada expresión a = 3, b = 2, c = –2 y calcula simplificando cada vez que sea necesario.

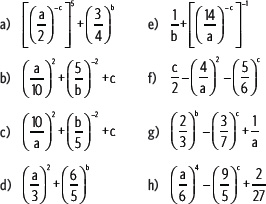
5. Resuelve los siguientes problemas.