Manual de preparación PSU Matemática

Actividades

1. Escribe

o

, según corresponda.

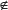
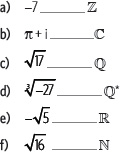
2. Determina la parte real y la parte imaginaria de cada número.

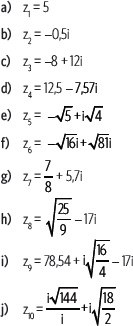
3. Escribe cada número en la forma z = a + bi según las condiciones dadas.

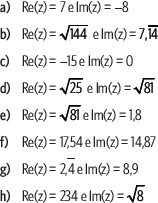
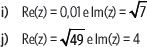
4. Escribe un número complejo que cumpla con la condición solicitada.

a) La parte real sea el doble de la parte imaginaria.

b) La parte imaginaria sea negativa y la parte real sea un número mayor que –5 y menor que cero.

c) Su parte real sea cero y su parte imaginaria sea un número par primo.

d) Su parte imaginaria sea cero y su parte real 7.

e) La parte real sea menor que 3 y mayor que 1 y la parte imaginaria sea un número negativo.

f) La parte real sea un múltiplo de 5 y la parte imaginaria sea divisor de 8.

5. Resuelve.

a) Si z = x + (16 + y)i, w =

– 7yi, ¿cuáles son los valores de x e y para que z = w?

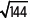
b) Si z1 = (5a + 12) + 7i, z2 = 17 – bi, ¿cuáles son los valores de a y b para que z1 = z2?

c) Si z = (x + 2y) + (5 + 7y)i, w =

– (5 – 12y)i, ¿cuáles son los valores de x e y para que z = w?

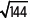
d) Si z1 = z2 y z1 = 3 – (5 + y)i, z2 = (4 – 2x) + (7 – 5y)i, ¿cuáles son los valores de x e y?

e) Si z = 3x + (5y – 4)i, w = 15 – 8yi, para que z = w, ¿cuánto es x + y?

6. Determina los valores de p y q para que se cumpla cada igualdad.

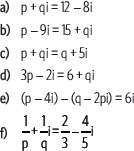
4.3 Representación gráfica de números complejos

En el plano cartesiano se utilizan los ejes X e Y, que representan los números reales. Es posible construir el plano complejo, que se conoce como plano de Argand, identificando el eje Y con las partes imaginarias (Im(z)) y el eje X con las partes reales (Re(z)). De esta manera, es posible representar un número complejo cualquiera como un punto en este plano identificando su parte real en el eje X, y su parte imaginaria en el eje Y.

Un número complejo z se puede representar en:

• Forma binomial: z = a + bi

• Forma cartesiana: z = (a, b)

Conjugado de un número complejo

Se define el conjugado

de un número complejo z = a + bi, como:

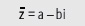
De lo anterior se deduce lo siguiente.

• El conjugado de un número cuya parte imaginaria es cero, es el mismo número.

Si z = a ⇒

= a.

• El conjugado del conjugado de un número complejo es el mismo número complejo.

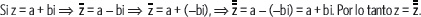
• Un número complejo z y su conjugado

se ubican en forma simétrica respecto al eje real del plano de Argand.

Módulo de un número complejo

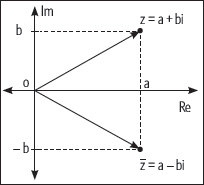
En el plano de Argand, el número complejo z = a + bi o z = (a, b), se representa utilizando un vector desde el origen del plano hasta el punto z. La longitud del vector corresponde al módulo del número complejo, que se anota por |z| y se calcula por:

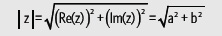
Actividades resueltas

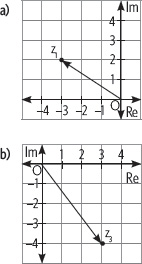
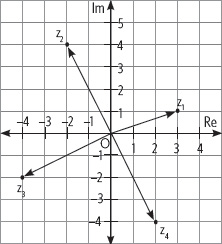
1. En el plano de Argand se han representado los números complejos z1, z2, z3 y z4. ¿Cuál es su representación en forma binomial y cartesiana?

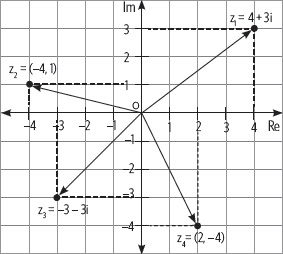
2. Si z1 = 3 – 5i, z2 = –5 + 8i y z3 = –1,5 – 7i, ¿cuáles son los conjugados?

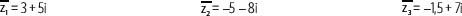
3. Representa en el plano el número complejo z = –3 + 2i, su conjugado y luego calcula su módulo.

El conjugado del número complejo es

, y su módulo es:

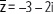
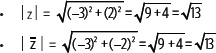
Además se observa que

.

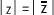
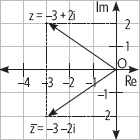
Actividades

1. Representa en el plano de Argand los siguientes números complejos.

a) z1 = 2

b) z2 = 3i

c) z3 = 4 – 4i

d) z4 = –3 – i

e) z5 = –4 + 5i

f) z6 = 3 + i

g) z7 = 5 – 2i

h) z8 = 7 – 5i

i) z9 = 6 – 4i

j) z10 = –5 – 2i

2. Observa el plano de Argand, luego responde.

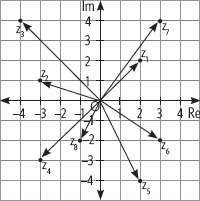
a) Escribe en forma binomial y cartesiana los números complejos que tienen la parte real e imaginaria mayor que cero.

b) Escribe en forma binomial y cartesiana los números complejos que tienen la parte real menor que cero e imaginaria menor que cero.

c) Escribe en forma binomial y cartesiana los números complejos que tienen la parte real mayor que cero e imaginaria menor que cero.

d) Escribe en forma binomial y cartesiana los números complejos que tienen la parte real menor que cero e imaginaria mayor que cero.

3. Calcula el módulo de cada número complejo y su conjugado, luego represéntalo en el plano de Argand.

a) z1 = –2 – i

b) z2 = –4 + 2i

c) z3 = 1 + 4i

d) z4 = 2 – 2i

e) z5 = 4 + 2i

f) z6 = –i

g) z7 = –2 – 5i

h) z8 = 8 + 2i

i) z9 = 3 – 8i

j) z10 = –5 – 4i

4. Determina el módulo y el conjugado de cada número complejo según corresponda.

4.4 Adición en

Para resolver una adición entre dos o más números complejos se suman, respectivamente, las partes reales y las partes imaginarias.

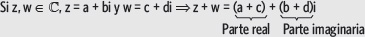
Actividades resueltas

1. Si z1 = –3 + 2i, z2 = 5 – 6i, luego z1 + z2 = (–3 + 5) + (2 – 6)i = 2 – 4i.

2. Si z1 = –8 – 4i, z2 = –12 – 8i, luego z1 + z2 = (–8 – 12) + (–4 – 8)i = –20 – 12i.

Propiedades de la adición de números complejos

En el conjunto

se cumplen las siguientes propiedades para la adición:

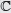
Clausura: si z, w

, entonces, z + w

.

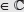
Conmutativa: si z, w

, entonces z + w = w + z.

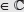
Neutro aditivo: existe un número complejo 0 tal que z + 0 = z.

Inverso aditivo: existe –z

tal que z + (–z) = 0.

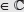
Asociativa: los sumandos se pueden agrupar de diferentes formas sin alterar el resultado, es decir, (z + w) + u = z + (w + u).

Al relacionar la adición con el conjugado de un número complejo se cumple que:

Si z = a + bi, se tiene que z +

= 2a, ya que z +

= (a + a) + (b + (–b))i = 2a

Si z = a + bi y w = c + di, se tiene que

, ya que:

Interpretación geométrica de la adición de números complejos

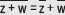
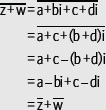
Al representar gráficamente la adición entre dos números complejos, esta se puede relacionar con un paralelógramo. Donde cada sumando corresponderá a un lado y la suma a la diagonal.

Si z1, z2 y z3

, se tiene:

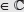
• z1 + z2 = z3

Actividad resuelta

Si (7 + 4i) + z = 2 + 7i, ¿cuál es el número complejo z?

Si z = a + bi, se tiene (7 + 4i) + (a + bi) = 2 + 7i ⇒ (7 + a) + (4 + b)i = 2 + 7i

Igualando las partes reales e imaginarias se obtiene lo siguiente:

• Parte real: 7 + a = 2 ⇒ a = –5

• Parte imaginaria: 4 + b = 7 ⇒ b = 3

Por lo tanto, z = –5 + 3i.

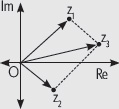
Actividades

1. Si z1 = 5 + 2i, z2 = –7 – 8i, z3 = –i, z4 = 5 – 2i, calcula:

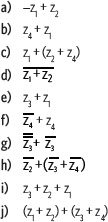
2. Representa en un solo plano de Argand cada adición entre números complejos.

a) z1 = 3 – 2i, z2 = 1 + 2i; A = z1 + z2

b) z3 = 7 + i, z4 = –3 + 2i; B = z3 + z4

c) z5 = 1 – i, z6 = 4 – 5i; C = z5 + z6

d) z1 = 2 – 2i, z2 = 4 + i; D = z1 + z2

e) z3 = –3 + i, z4 = 1 + i; E = z3 + z4

f) z5 = 1 – 2i, z6 = 3i; F = z5 + z6

g) z1 = –2i, z2 = –5 + i; G = z1 + z2

h) z3 = – i, z4 = 2i; H = z3 + z4

i) z5 = 6 – i, z6 = 3 + 3i; I = z5 + z6

j) z1 = 7 – 2i, z4 = 5 – 5i; J = z1 + z4

3. Verifica si cada afirmación es verdadera o falsa.

a) El inverso aditivo de z = 1 + i es w = –1 + i.

b) Siempre la suma de números complejos es un número real.

4. Observa el plano de Argand y luego resuelve o responde según corresponda.

5. Resuelve.

a) Si (9 – 3i) + z = 15 + i, ¿cuál debe ser el número complejo z?

b) Si w + (–6 – 2i) = 17 + 3i, ¿cuál debe ser el conjugado de w?

c) Si z = –6 + bi, w = c + 7i y además z + w = –9 – 15i, ¿cuáles son los valores de b y c?

4.5 Sustracción en

Para resolver una sustracción entre dos o más números complejos se restan, respectivamente, las partes reales y las partes imaginarias.

Si z, w

, z = a + bi, w = c + di ⇒ z – w = (a – c) + (b – d)i

Al relacionar la sustracción con el conjugado de un número complejo, se tiene lo siguiente:

• Si z = a + bi, se tiene que z –

= 2bi.

z –

= (a + bi) – (a – bi) = (a – a) + (b – –b)i = (b + b)i = 2bi

• Considerando z

, se cumplen las siguientes igualdades:

• Si z = a + bi y w = c + di, se tiene

Actividades resueltas

1. Si z = 5 – 7i, w = – 7 + 6i, ¿cuánto es z – w?

z – w = (5 – –7) + (–7 – 6)i = 12 – 13i

2. Si (– 4 + 2i) – z = –3 + 2i, ¿cuál debe ser el número complejo z?

Si z = a + bi, se tiene:

(–4 + 2i) – (a + bi) = –3 + 2i ⇒ (–4 – a) + (2 – b)i = –3 + 2i

Igualando sus partes real e imaginaria se obtiene:

• Parte real: –4 – a = –3 ⇒ a = –1

• Parte imaginaria: 2 – b = 2 ⇒ b = 0

Por lo tanto, z = –1.

Nota histórica

Si bien los números imaginarios eran conocidos desde el siglo XVI, no fue hasta principios del siglo XIX que se les dio validez a partir de su interpretación geométrica (plano de Argand). Esta interpretación fue dada casi simultáneamente por el matemático Carl F. Gauss (1777-1855) y dos aficionados a la matemática: un noruego de apellido Wessel (1745-1818) y un tenedor de libros parisino llamado Argand (1768-1822).

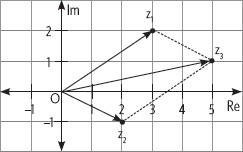
3. Si z1 = 3 + 2i, z2 = 2 – i, z3 = 5 + i, resuelve y representa las siguientes sustracciones: z3 – z2 y z3 – z1.

z3 – z2 = (5 + i) – (2 – i)

= 3 + 2i

= z1

z3 – z1 = (5 + i) – (3 + 2i)

= 2 – i

= z2

Actividades

1. Si z1 = 6 – 4i, z2 = –4i, z3 = –3 + 2i, z4 = 6 + 4i, calcula.

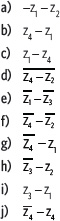
2. Si z1 = 3 – 4i, z2 = –5 – 2i, z3 = –2 – 6i, z4 = –3 + 4i, calcula y luego representa en un plano de Argand lo siguiente.

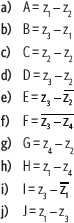
3. Verifica si la afirmación es verdadera o falsa. Justifica tu respuesta.

a) La sustracción entre un número complejo y su conjugado da como resultado un número real.

b) La diferencia entre números complejos cumple la propiedad asociativa.

c) El resultado de (1 – i) – (1 + i) – (–1 – i) es igual a 1.

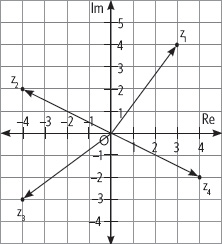
4. Observa el plano de Argand y luego resuelve.

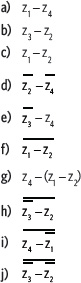
5. Resuelve.

a) Si (3 – 5i) – z = 14 + 5i, ¿cuál debe ser el número complejo z?

b) Si w – (–6 + 13i) = 8 – 5i, ¿cuál debe ser el conjugado del número complejo w?

c) Si z = a – (3 – b)i, w = 12 + (5 – 4b)i y además w – z = –5 – 4i, ¿cuáles son los valores de a y b?

6. Demuestra las siguientes igualdades.

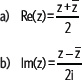
4.6 Multiplicación en

La multiplicación entre dos números complejos z = a + bi, w = c + di se define por:

z • w = (a + bi) • (c + di) = (ac – bd) + (ad + bc)i

Propiedades de la multiplicación en

En

se cumplen las siguientes propiedades para la multiplicación:

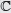
Clausura: si z, w

, entonces z • w

.

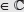
Conmutativa: si z, w

, entonces z • w = w • z.

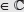
Neutro multiplicativo: z • 1 = 1 • z, = z ∀ z

.

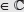
Inverso multiplicativo: si z = a + bi ≠ 0, existe

i

tal que z • z–1 = 1 = 1 + 0i.

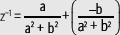
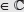
Asociativa: si z, w, u

, entonces (z • w) • u = z • (w • u).

La propiedad distributiva de la multiplicación respecto de la adición o de la sustracción.

∀ z, w, u

, entonces z • (w ± u) = z • w ± z • u.

Al relacionar la multiplicación con el conjugado de un número complejo, se tiene que:

• Si z = a + bi, entonces

= |z|2, ya que

= (a + bi) • (a – bi)

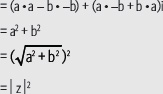
• Si z = a + bi y w = c + di, entonces