
Полная версия
Manual de preparación PSU Matemática
a) La diferencia de dos números enteros positivos es siempre positiva.
b) La diferencia de un número entero positivo con un entero negativo es siempre negativa.
c) La diferencia entre dos números enteros es igual a la suma del minuendo con el inverso aditivo del sustraendo.
d) La diferencia entre un número entero y su doble es igual al inverso aditivo del número.
4. Completa los siguientes cuadrados mágicos teniendo en cuenta que la suma de tres casillas de cada columna, fila y diagonal en ambos sentidos debe ser la misma.
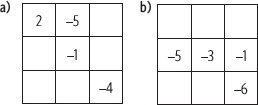
5. Resuelve los siguientes problemas.
a) Un radar registra el movimiento de un submarino. Si inicialmente el submarino se encuentra a 32 m bajo el nivel del mar y luego desciende 23 m, ¿a qué profundidad se encuentra el submarino?
b) La parte más profunda de una mina está a 120 m por debajo del nivel de la Tierra. ¿A qué distancia de la superficie se encuentran dos mineros que ascendieron 85 m a partir del punto más hondo de la mina?
c) Un termómetro marcaba 8 grados bajo cero a las 7 de la mañana. Cinco horas más tarde subió 9 grados y 6 horas después bajó 5 grados. ¿Qué temperatura marcó finalmente?
d) El Partenón de Atenas se construyó aproximadamente en el año 432 a. C. y la Torre Eiffel se terminó de levantar en 1889. ¿Cuántos años transcurrieron entre la construcción de ambas edificaciones?
e) En la mañana la temperatura de una ciudad fue de 3 grados bajo cero. Si durante el día la temperatura se incrementó en 5 °C, ¿cuál fue la temperatura al final del día?
1.4 Multiplicación y división en 

Para calcular el producto de dos números enteros se puede considerar la regla de los signos:
• Si los factores tienen el mismo signo, el producto es positivo.
• Si los factores tienen distinto signo, el producto es negativo.
Regla de los signos + • + = + + • – = – – • – = + – • + = –Actividades resueltas
1. Calcula el producto en cada caso.
a) (–12) • (–6)
Como 12 • 6 = 72, entonces al usar la regla de los signos se tiene: (–12) • (–6) = 72.
b) (–15) • 7
Como 15 • 7 = 105, entonces, al usar la regla de los signos se tiene: (–15) • 7 = –105.
2. Resuelve los siguientes problemas.
a) Una tortuga marina desciende 2 metros cada minuto. ¿A qué profundidad estará después de 4 minutos?
Resolución: se representan los datos con números enteros.
Por cada minuto desciende 2 m: –2.
Después de 4 minutos: 4.
Luego, la tortuga estará a: 4 • (–2) = –8.
Respuesta: La tortuga estará a 8 metros de profundidad.
b) Un agente financiero observa que las acciones de la compañía en que pensaba invertir hace tres semanas tuvieron una pérdida de $ 5.000 por acción semanalmente. ¿Cuánto dinero no perdió el agente, por concepto de acción, gracias a que no invirtió en esa compañía?
Resolución: se representan los datos con números enteros.
Por cada semana la acción pierde $ 5.000, es decir, –5.000.
Hace tres semanas: –3
Luego, se tiene que: (–5.000) • (–3) = 15.000.
Respuesta: El agente no perdió $ 15.000 por acción.

Para calcular el cociente de dos números enteros se puede considerar la regla de los signos:
• Si el dividendo y el divisor tienen el mismo signo, entonces, el cociente es positivo.
• Si el dividendo y el divisor tienen distinto signo, entonces, el cociente es negativo.
Regla de los signos + : + = + + : – = – – : – = + – : + = –Actividad resuelta
Calcula las siguientes divisiones entre números enteros.
a) (–165) : 11
Como 165 : 11 = 15, entonces por la regla de los signos (–165) : 11 = –15.
b) (–325) : (–13)
Como 325 : 13 = 25, entonces, por la regla de los signos (–325) : (–13) = 25.
Actividades
1. Calcula el producto en cada caso.
a) (–3) • (4) • (–6)
b) (–10) • (9)
c) (–4) • (–2) • (–6) • (–3)
d) (6) • (5) • (–3) • (–1)
e) 9 • (–8)
f) (4) • (3) • (–12)
2. Analiza la siguiente expresión. Luego, resuelve.
x @ y = –7 • x • (108 : y)
a) 4 @ 2
b) 6 @ 4
c) 7 @ 9
d) –5 @ 3
e) –3 @ 6
f) –8 @ 12
g) 2 @ 4
h) 5 @ 1
i) 6 @ –6
j) 0 @ 1
3. Determina el término desconocido en cada caso.
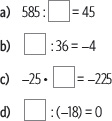
4. Resuelve los siguientes problemas.
a) La temperatura de un refrigerador disminuye 3 °C cada hora. ¿En cuánto disminuirá la temperatura del refrigerador al cabo de 8 horas?
b) Con una perforadora de petróleo se excavó un pozo de 1.248 metros en 12 días trabajando 8 horas diarias. Si cada hora se profundizó la misma cantidad de metros, ¿cuántos metros se excavaron en una hora?
c) Si las acciones de cierta compañía disminuyen su rentabilidad en $ 18 cada mes, ¿cuánto habrá perdido al cabo de 3 años?
5. Responde.
a) Una multiplicación tiene 136 factores y todos son negativos. ¿Cuál es el signo del producto?
b) En una división el dividendo es negativo y el divisor es positivo. ¿Cuál es el signo del cociente?
6. Ejemplifica cada afirmación.
a) El producto de cinco factores pares negativos es negativo.
b) El doble de un número entero puede ser menor que el número.
c) La quinta parte de un número divisible por 10 puede ser un entero negativo menor que –20.
d) La división exacta entre un número de la forma –1.2
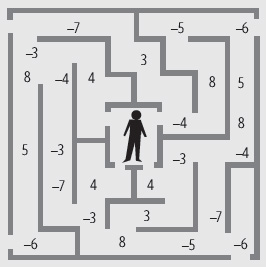
7. Encuentra el camino que siguió Miguel para salir del laberinto, teniendo en cuenta que lo recorrió en el orden de los cocientes de las siguientes divisiones y que no pasó dos veces por el mismo punto del trayecto.
a) (–12) : (–3)
b) (–15) : (5)
c) (21) : (–3)
d) (–45) : (15)
e) (48) : (–12)
f) (–72) : (–9)
g) (80) : (16)
h) (66) : (–11)
2. Números racionales (
2.1 El conjunto de los números racionales

El conjunto de números racionales, que se simboliza

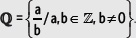
Entre los conjuntos numéricos estudiados se tiene que:

Actividad resuelta
Escribe el número racional asociado a la siguiente situación.
Si un pastel se divide en 8 partes iguales, ¿qué fracción del pastel representa cada una de ellas?
El número racional





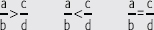
Para que
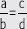


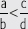

Por ejemplo,


Actividades resueltas
1. Determina si las siguientes fracciones representan el mismo número racional. Justifica tu respuesta.
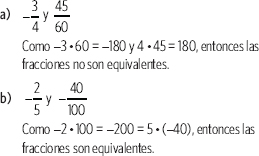
2. Ordena de menor a mayor los siguientes números racionales 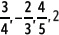
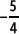
Se expresan los números como fracciones equivalentes con igual denominador.
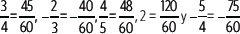
Se ordenan las fracciones equivalentes:
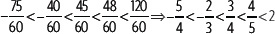

Para representar en la recta numérica un número racional escrito como fracción, se pueden considerar los siguientes pasos:
1° Se determina entre qué números enteros consecutivos está el número racional.
2° Se divide la unidad que hay entre los dos números enteros en tantas partes como indica el denominador.
3° A partir del menor de los dos números enteros, se consideran hacia la derecha tantas partes como indica el numerador, si el número es positivo. Si el número es negativo, a partir del entero mayor se toma hacia la izquierda tantas partes como indica el numerador.
Actividad resuelta
Representa en la recta numérica el número racional 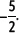
Para representar en la recta numérica
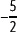
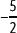
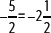
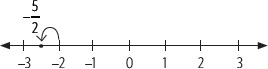
Actividades
1. Escribe tres fracciones equivalentes a cada número racional.
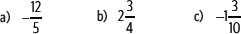
2. Compara cada par de fracciones y escribe >, < o = según corresponda.
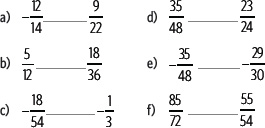
3. Ordena de mayor a menor en cada caso.
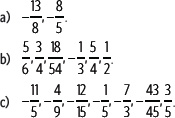
4. Determina si cada proposición es verdadera o falsa. Justifica tu respuesta.

5. Escribe los números racionales representados con un • en cada recta.
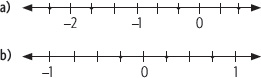
2.2 Representación decimal de un número racional


• Finitos: son aquellos que tienen una cantidad finita de cifras decimales.
• Infinitos: son aquellos que tienen una o varias cifras que se repiten infinitamente (período).


1˚ Se escriben en el numerador todas las cifras del número sin considerar la coma.
2˚ En el denominador se escribe el valor de la potencia de 10 que tiene tantos ceros como cifras decimales tenga el número.
3˚ Si es posible, se simplifica hasta obtener una fracción irreducible.
Actividad resuelta
Representa el número 5,29 como una fracción.
Como 5,29 es un decimal finito, se puede verificar que 5,29 =
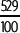

1˚ Se escribe en el numerador la diferencia entre el número formado por las cifras hasta el final del primer período, sin considerar la coma, y la parte entera del número.
2˚ En el denominador se escriben tantos nueves como cifras tenga el período.
3˚ Si es posible, se simplifica hasta obtener una fracción irreducible.
Actividad resuelta
Representa el número 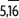
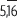
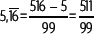
Se puede comprobar resolviendo la división, esto es, 511 : 99 = 5,161616...

1˚ Se escribe en el numerador la diferencia entre el número formado por las cifras hasta el final del primer período, sin la coma, y el número formado por la parte entera y el anteperíodo.
2˚ En el denominador se escriben tantos nueves como cifras tenga el período, seguido de tantos ceros como cifras tenga el anteperíodo.
3˚ Si es posible, se simplifica hasta obtener una fracción irreducible.
Actividad resuelta
Representa el número 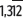
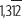
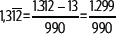
Se puede comprobar resolviendo la división, esto es, 1.299 : 990 = 1,31212...
Actividades
1. Completa la tabla. Parte entera
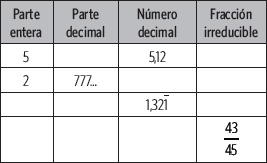
2. Expresa cada número decimal como una fracción irreducible.

3. Expresa cada número decimal como una fracción irreducible. Luego, represéntalo en la recta numérica.
a) 2,5
b) 0,25
c) 4,5
d) 3,5
e) 1,5
f) 1,25
4. Determina cuáles de las siguientes proposiciones son verdaderas y cuáles son falsas. Justifica tu respuesta.

5. Escribe un número decimal que cumpla cada condición. Luego, represéntalo como una fracción.
a) Es decimal finito y tiene 38 milésimas.
b) Es decimal periódico y tiene parte entera 6.
c) Es decimal semiperiódico y su anteperíodo es 13.
6. Los resultados de una prueba académica se obtuvieron dividiendo la cantidad de respuestas correctas por la cantidad de preguntas de la prueba (90). Si respondieron toda la prueba y considerando la siguiente tabla que muestra los resultados de tres estudiantes:
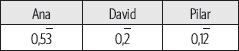
a) Determina la fracción que representa el resultado de cada estudiante.
b) ¿Cuántas preguntas correctas respondió cada estudiante?
c) ¿Cuántas respuestas incorrectas obtuvo cada uno?
7. Observa y responde.
La siguiente gráfica muestra las distancias de tres islas a la costa.
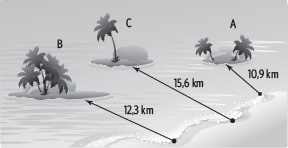
a) Representa las distancias de las islas en la recta numérica.



