Manual de preparación PSU Matemática

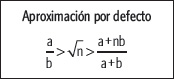
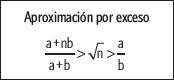
Actividad resuelta

Calcula una aproximación de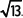

.

Una fracción que cumple

. Como 16 > 13 > 9, entonces 4 >

> 3. Considerando 4 >

, aproximando por defecto se tiene:

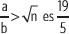
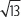
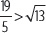
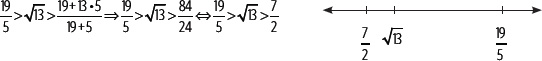
Ahora, aproximando por exceso, se considera que

.

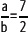
Luego, se tiene que:

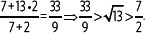
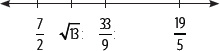
Se puede aplicar este proceso reiteradamente para obtener una mejor aproximación.

Aproximación por acotación sucesiva

Se acota el número irracional x, tanto inferior como superiormente, es decir, se determinan dos números racionales a y b tal que a < x < b, luego se calcula el promedio entre estos números y se prosigue tantas veces como sea necesario.

Actividad resuelta

Determina una aproximación

.

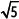
El proceso continúa tantas veces como se quira, según la aproximación conseguida.

Orden en

es un conjunto ordenado. Asi, para comparar numeros reales, y en particular numeros irracionales, se pueden representar como numeros decimales, para luego compararlos. Una manera alternativa si se consideran raices cuadradas, consiste en com-parar sus cuadrados, ya que para numeros mayores que 1, mientras mayor sea un numero, mayor es su expresion al cuadrado.

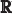
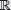
Actividad resuelta

Ordena de menor a mayor

.

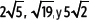
Al elevarlas al cuadrado resulta:

= 50, luego se tiene lo siguiente:

.

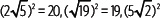
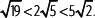
Actividades

1. Aproxima por truncamiento y redondeo cada número.

a) 3,14151617… a la centésima.

b) 15,3698765… a la décima.

2. Aproxima las siguientes raíces utilizando cada método según corresponda.

3. Ordena de menor a mayor según corresponda.

3.8 Números irracionales en la recta numérica

Para ubicar números irracionales en la recta numérica es necesario aproximarlos, ya que tienen infinitas cifras decimales. Por ejemplo, para π se puede considerar 3,1415 y se marca dicha aproximación con un punto en la recta. Sin embargo, para situar en la recta numérica la raíz cuadrada de un número natural, es posible utilizar algún procedimiento geométrico.

Actividad resuelta

Ubica el número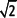

en la recta numérica.

Sobre el número 1 se traza un segmento AB perpendicular que mida 1 unidad, luego se forma un triángulo uniendo el número 0 con B. Al aplicar el teorema de Pitágoras se tiene que la hipotenusa mide

, luego con centro en 0 y radio igual a la hipotenusa se traza un arco de circunferencia que corta a la recta numérica en

.

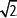
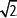
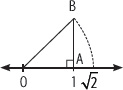
Prosiguiendo de esta forma se pueden ubicar en la recta numérica

, etc.

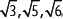
Esta construcción geométrica que representa las raíces cuadradas de los números naturales se conoce como la espiral de Teodoro.

Actividades

1. Determina qué número se ha representado con una letra en la recta numérica.

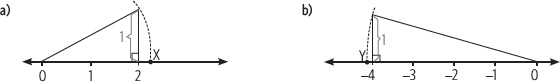
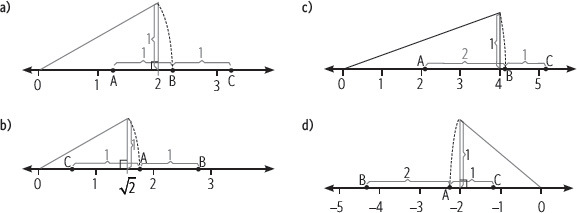
2. En cada recta numérica determina qué números representan las letras A, B y C.

3.9 Logaritmos

El logaritmo de a en base b (logb a) es el exponente de una potencia de base b cuyo valor es a, es decir, si a

, b

– {1} y x

, se define lo siguiente:

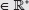
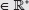
logb a = x ⇔ bx = a

Para relacionar la potencia, el logaritmo y la raíz enésima, con n

y a, b

, b ≠ 1, se tiene lo siguiente:

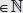
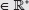
bn = a ⇔ n = logb a ⇔ b =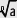

Cuando la base del logaritmo es 10 log10 a = log a.

El logaritmo de base e se conoce como logaritmo natural. Así, loge a = ln a.

Actividades resueltas

1. Calcula el valor de log5 125.

Por definición se tiene que: log5 125 = x ⇔ 5x = 125. Como 53 = 125, se tiene que x = 3.

2. Si logx 8 = 3, ¿cuál es el valor de x?

Se sabe que logx 8 = 3 ⇔ x =

, luego x = 2.

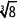
3. ¿Cuál es el valor de log 10.000?

Considerando x = log 10.000 ⇔ 10x = 10.000, se obtiene que x = 4, luego log 10.000 = 4.

4. Si ln x = 0 y log y = 5, ¿cuál es el valor de x + y?

De ln x = 0 se obtiene que e0 = x, luego 1 = x; además, de log y = 5 ⇔ 105 = y, se obtiene que y = 100.000. Por lo tanto, x + y = 100.001.

Actividades

1. Calcula.

2. Calcula el valor de las siguientes expresiones.

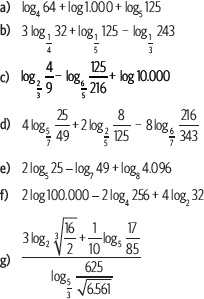
3.10 Propiedades de los logaritmos

El logaritmo cumple las siguientes propiedades:

• Logaritmo de la unidad. Si b

– {1}, entonces:

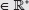
logb 1 = 0

• Logaritmo de un producto. Si a

– {1}, b, c

, entonces:

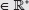
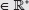
loga (b • c) = loga b + loga c

• Logaritmo de una potencia. Si a

– {1}, b

entonces:

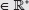
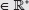
loga bn = n • loga b

• Logaritmo de la base. Si b

– {1}, entonces:

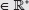
logb b = 1

• Logaritmo de un cociente. Si a

– {1}, b, c

, entonces:

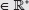
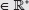
• Cambio de base de un logaritmo. Si a, b, c

– {1}, entonces:

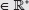
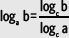
Actividades resueltas

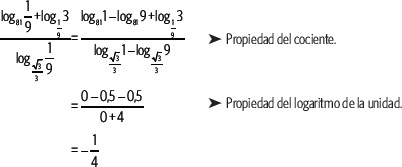
1. Calcula el valor de la expresión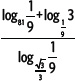

.

2. Utilizando las propiedades estudiadas, calcula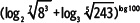

.

Actividades

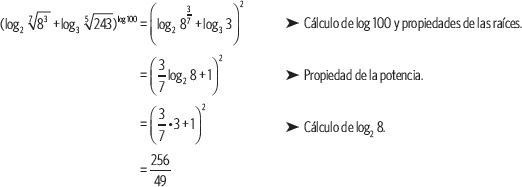
1. Calcula el valor de cada expresión.

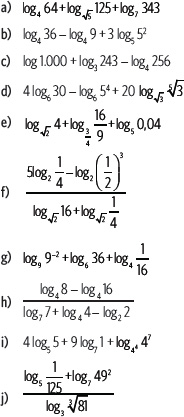
2. Considerando log3 5 = 1,465, log3 7 = 1,771, log6 5 = 0,898 y log6 2 = 0,387, calcula los siguientes logaritmos.

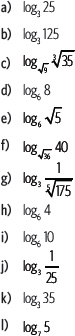
3. Reduce cada expresión. Para ello, aplica las propiedades del logaritmo.

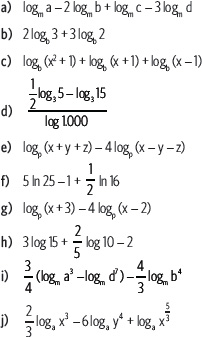
4. Determina si las siguientes igualdades son verdaderas o falsas. Justifica en cada caso.

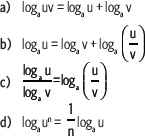
5. Resuelve.

a) Si M • N3 • P = 625, ¿cuál es el valor de la expresión

?

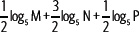
b) Si A = (log2 80 – log2 5) + (log3 135 – log3 5), ¿cuánto es A2?

c) Calcula el valor de la expresión A = log6 (log3 (log2 (log2 256))).

d) ¿Cuál es el valor de la expresión

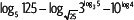
e) Si F = 4 log16 (log8

), ¿cuál es el valor de 3F?

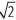
f) Se define B = log30 64 + log30 153 – 3 log30 2. ¿Cuál es el valor de log3 B2?

4. Números complejos (

)

4.1 Números imaginarios II

Las ecuaciones de la forma x2 + a = 0, a

, no tienen solución en el conjunto numérico de los números reales porque el cuadrado de un número real es un número no negativo y al ser sumado con un número positivo su resultado no es cero. En particular en la ecuación x2 + 1 = 0, si tuviese solución en el conjunto de los números reales, debiese existir un número real con la condición de que x2 = –1. Para resolver el problema se define el número i (unidad imaginaria) como el número cuyo cuadrado es –1, es decir, i2 = –1. Por lo tanto la ecuación x2 + 1 = 0 tiene como soluciones x1 = i, x2 = –i.

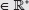
Las ecuaciones de la forma x2 + a = 0, con a

, tienen dos raíces o soluciones imaginarias que son:

Potencias de i

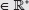
En el desarrollo de potencias de i se tiene:

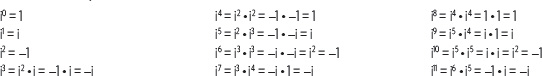
En general, se tiene ∀ p

:

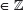
Actividades resueltas

1. Determina si las siguientes ecuaciones tienen solución en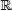

.

a) x2 + 10 = 0

Al despejar se obtiene x2 = –10. Luego, no existe un número real que al elevarlo al cuadrado resulte –10. Por lo tanto, no tiene solución en

.

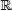
b) 4x2 – 16 = 0

Al despejar se obtiene x2 = 4. Luego se tiene que existen dos números reales que cumplen la igualdad: 2 y –2. Por lo tanto, tiene solución en

.

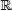
2. Resuelve las siguientes ecuaciones.

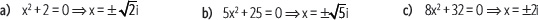
3. Calcula el valor de cada potencia.

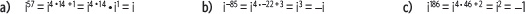
4. Calcula el resultado de cada expresión.

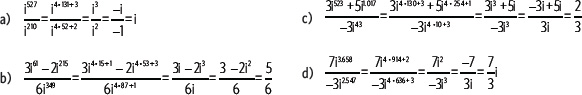
Actividades

1. Determina cuál de las siguientes ecuaciones no tiene solución en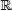

.

a) x2 + 6 = 0

b) x2 – 5 = 0

c) 5x2 – 25 = 0

d) 0 = 4x2 + 32

e) 0 = 12(x2 + 3)

f) 15 = 7x2 – 15

g) 8(x2 + 12) = 16(x2 – 7)

2. Resuelve las siguientes ecuaciones.

a) x2 + 5 = 0

b) 0 = 150 + x2

c) x2 + 12 = 0

d) –x2 = 200

e) x2 + 16 = 0

f) –5x2 = 500

g) 0 = 25 + x2

h) –8x2 = 288

i) 0 = 100 + x2

j) –9x2 = 81

3. Calcula el valor de cada potencia de i, luego resuelve.

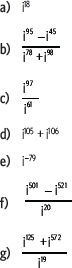
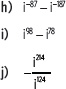
4. Determina el resultado de cada expresión.

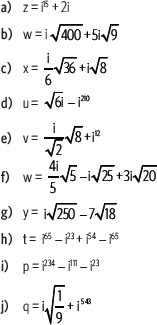
5. Verifica si cada afirmación es verdadera o falsa. Justifica en cada caso.

a) Toda expresión de la forma

, a

, representa un número imaginario.

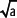
b) Al calcular i

se obtiene como resultado –9.

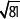
c) Al calcular i456 su resultado es un número real.

d) El resultado de i–7 es un número imaginario.

6. Calcula cada suma.

a) i3 + i6 + i9 + ... + i96 + i99

b) i2 + i4 + i6 + ... + i98 + i100

4.2 Números complejos (

)

El conjunto de los números complejos (

) está formado por los números de la forma z = a + bi con a, b

.

= {z = a + bi / a, b

}

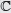
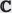
En todo número complejo z = a + bi se distinguen dos partes: la parte real de z simbolizada por Re(z) = a, y la parte imaginaria de z simbolizada por Im(z) = b.

Los números reales y los números imaginarios son subconjuntos de los números complejos, ya que:

• Números reales: números complejos de la forma z = a + 0i, es decir, Im(z) = 0.

• Números imaginarios: números complejos de la forma z = 0 + bi, es decir, Re(z) = 0.

Igualdad entre números complejos

Dos números complejos z1 y z2 son iguales si sus partes real e imaginaria son respectivamente iguales. Es decir:

z1 = z2 ⇔ Re(z1) = Re(z2) e Im(z1) = Im(z2)

Entre los conjuntos numéricos estudiados, se tiene lo siguiente:

.

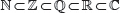
Representado en un diagrama, se tiene:

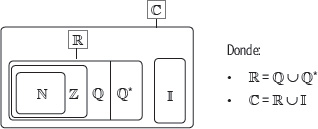
Actividades resueltas

1. Determina la parte real e imaginaria de cada número complejo.

2. Si z1 = (12x – 6) + 8i, z2 = 18 + (5 – y)i, ¿cuáles son los valores de x e y para que z1 = z2?

Se debe cumplir Re(z1) = Re(z2) e Im(z1) = Im(z2), es decir:

• 12x – 6 = 18 ⇒ x = 2

• 8 = 5 – y ⇒ y = –3

Remplazando estos valores se tiene: z1 = z2 = 18 + 8i.