
Полная версия
Manual de preparación PSU Matemática
Estructura del Manual
El manual de preparación Matemática PSU está estructurado en 4 capítulos:
• Números
• Álgebra
• Geometría
• Estadística y probabilidad
Cada uno de los cuales se encuentra en directa concordancia con el temario del DEMRE.
Al iniciar cada capítulo se presentan los temas que se estudiarán en ellos.

El manual tiene también una sección de Anexos, la que incorpora los contenidos de:
• Razones y proporciones
• Proporcionalidad
• Porcentajes
• Trigonometría
• Tabla de distribución normal
En cada capítulo se explican diferentes temas en donde se presentan la formalización del concepto tratado, Actividades resueltas para ejemplificar cada contenido y Actividades para ejercitar lo estudiado.
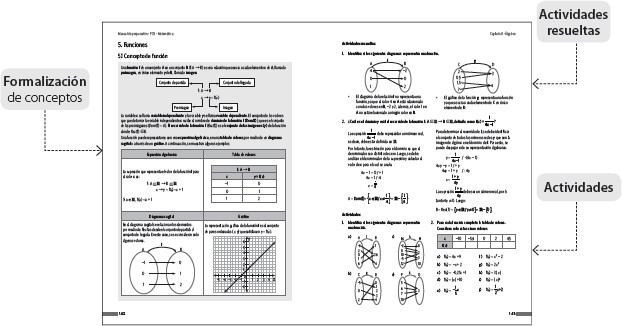
Además, el Manual PSU cuenta con un Cuaderno de ejercicios estructurado según los siguientes ejes: Números, Álgebra, Geometría y Estadística y probabilidad. Al comenzar la ejercitación de cada eje encontrarás un grupo de reactivos resueltos para enfrentar de mejor manera cada uno de los Tests que se proponen, y al finalizar el Cuaderno de ejercicios podrás ejercitar con un ensayo tipo PSU alineado al temario DEMRE.
Capítulo I
Números
Temas
1. Números enteros (
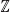
2. Números racionales (
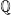
3. Números reales (
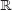
4. Números complejos (
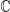
1. Números enteros (
1.1 El conjunto de los números enteros


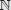
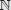
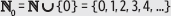
Para representar algunas situaciones o problemas de la vida diaria, los números naturales no son suficientes. Por ejemplo:
• Representar un sobregiro de $ 200.000 en una cuenta corriente.
• Determinar la temperatura de una ciudad si en un instante es de 5 °C y una hora después baja 7 °C.
• Determinar un número que sumado con 4 resulte 1, o sea, resolver la ecuación x + 4 = 1.







Actividad resuelta
Escribe un número entero que represente la información numérica de cada situación.
a) En la Antártica se registró una temperatura de 20 °C bajo cero.
Las temperaturas bajo cero se pueden representar con números enteros negativos. Así, la temperatura descrita correspondería a –20, es decir, –20 °C.
b) Las ganancias de una empresa en un día fueron $ 700.000.
Las ganancias se pueden representar con números enteros positivos. Así, las ganancias de la empresa corresponderían al número 700.000.

Si a, b, c ∈

El mínimo común múltiplo (m.c.m.) de un conjunto de números enteros es el menor entero positivo que es múltiplo de cada uno de los números dados.
El máximo común divisor (m.c.d.) de un conjunto de números enteros es el mayor entero positivo que divide a cada uno de los números del conjunto.
Un número entero es par si es múltiplo de 2.
n es par ⇔ n = 2p, con p ∈

Un número entero es impar si es antecesor o sucesor de un número par.
n es impar ⇔ n = 2p – 1 o n = 2p + 1, con p ∈

Actividades resueltas
1. ¿–20 es múltiplo de 10? Sí, porque –20 = (–2) • 10.
2. ¿2 es divisor de –20? Sí, porque –20 = 2 • (–10).
3. Determina el m.c.m. y el m.c.d. de los siguientes números enteros.
a) m.c.m.(–2, 6) = 6 m.c.d.(–2, 6) = 2
b) m.c.m.(–4, 4, 8) = 8 m.c.d.(–4, 4, 8) = 4
c) m.c.m.(–3, 5, 7) = 105 m.c.d.(–3, 5, 7) = 1
Actividades
1. Responde las siguientes preguntas.
a) ¿En qué situaciones se pueden usar números enteros?
b) ¿Cómo se distinguen los números enteros positivos de los números enteros negativos?
2. Escribe ∈ o ∉ según corresponda.
3. Determina cuáles de las siguientes proposiciones son verdaderas y cuáles son falsas. Justifica tu respuesta.
a) La sustracción es una operación que siempre tiene solución en el conjunto de los números naturales.
b) Los números enteros están conformados por los números enteros positivos, el cero y los números enteros negativos.
c) Algunos números naturales no son números enteros.
d) Todos los números enteros son positivos o negativos.
4. Representa la información numérica de cada situación con un número entero.
a) El avión vuela a 2.700 m de altura.
b) Un submarino se encuentra a 2.500 m bajo el nivel del mar.
c) La rueda se inventó aproximadamente en el año 5500 a. C.
d) Daniela tiene una deuda de $ 2.300 en el almacén.
e) El fondo del mar Caribe alcanza aproximadamente los 3.000 m de profundidad.
f) Alejandro Magno nació en el año 356 a. C. en Macedonia.
g) El récord mundial de inmersión libre masculino (buceo sin equipo) es de 120 m de profundidad.
5. Lee, observa y resuelve.
Para generar energía eléctrica a partir de yacimientos geotérmicos se deben perforar profundos pozos que conduzcan, hacia la superficie terrestre, el fluido almacenado a altas temperaturas en la corteza de la Tierra. Ya en la superficie, el vapor, que viene a alta presión, se utiliza para hacer funcionar una turbina y así producir energía eléctrica.
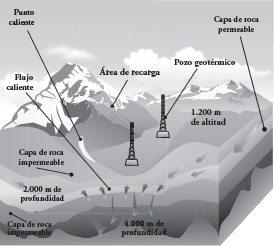
a) ¿Qué medidas de la ilustración anterior pueden ser representadas mediante números enteros?
b) ¿Cuáles corresponden a números positivos?, ¿cuáles a números negativos?
6. Determina si cada afirmación es verdadera o falsa.
a) El m.c.m.(4, 10) es un número par.
b) El m.c.d.(8, 12) es un número impar.
c) El m.c.m.(5, 15, 25) es igual que el m.c.m.(1, 2, 5).
d) El m.c.d.(12, 15, 21) es distinto al m.c.d.(9, 3, 6).
1.2 Representación, comparación y orden en 

Los números enteros se pueden representar en la recta numérica de la siguiente manera:
En un punto sobre la recta se ubica el número 0.

Se hacen marcas a la izquierda y a la derecha del cero, de tal forma que el espacio entre dos marcas consecutivas sea siempre el mismo.

Se asocia cada marca con un número entero. Para ello se ubican los enteros positivos a la derecha del cero y los enteros negativos a la izquierda.

Es importante considerar que a cada número le corresponde un único punto y que la distancia entre dos números enteros consecutivos siempre es la misma.
Actividad resuelta
Representa en una recta numérica los números enteros –6 y 3.
1° Se traza la recta y se ubica el cero.
2° Se dibujan marcas considerando que la distancia entre dos marcas consecutivas debe ser la misma.
3° Se ubica el número –6 a 6 unidades a la izquierda del cero y el número 3 a 3 unidades a la derecha del cero.


Dados dos números enteros a y b, entre ellos se puede presentar una y solo una de las siguientes relaciones de orden:
• a < b. En la recta numérica, a está a la izquierda de b.
• a > b. En la recta numérica, a está a la derecha de b.
• a = b. En la recta numérica, a y b se encuentran ubicados en el mismo punto.
En la recta numérica, será mayor aquel número entero que se ubique más a la derecha.
Actividad resuelta
Ubica cada par de números en una recta numérica y establece la relación de orden entre ellos.
a) –7 y –2.

Como –7 está a la izquierda de –2, entonces –7 es menor que –2, es decir, –7 < –2.
b) –5 y 4.

Como 4 está a la derecha de –5, entonces 4 es mayor que –5, es decir, 4 > –5.

El valor absoluto de un número a representa la distancia de este número al cero en la recta numérica. Se simboliza |a| y se lee ''valor absoluto de a''.
Para comparar dos números negativos se pueden analizar sus valores absolutos. De esta manera, un número negativo es menor que otro si su valor absoluto es mayor, es decir, si se ubica más a la izquierda en la recta numérica.
Actividad resuelta
Escribe <, >, o = según corresponda.
a) –13__________–8 Como |–13| = 13 > |–8| = 8, entonces en la recta numé-rica –13 está a la izquierda de –8. Por lo tanto, es menor, o sea, –13 < –8.
b) |–15|_______–|15| Primero, se determinan los valores absolutos. |–15| = 15 y |15| = 15. Por lo que se cumple que –|15| = –15. Finalmente, se tiene |–15| > –|15| porque todo número positivo es mayor que uno negativo.
Actividades
1. Responde las siguientes preguntas.
a) Si a, b ∈
b) ¿Qué número tiene como valor absoluto 10 y en la recta numérica se ubica a la izquierda de 0?
c) ¿Cuándo el valor absoluto de un número es mayor que el número?
d) Si a, b, c ∈
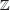
2. Escribe en cada recta numérica el número entero asociado a cada letra.
3. Observa y completa. Luego, responde.

a) ¿Cuál es el antecesor de –1?
b) ¿Cuál es el número entero cuyo sucesor es –2?
4. Responde. Justifica tu respuesta en cada caso.
a) ¿Cuántos números enteros están localizados entre –14 y 3? ¿Cuáles son estos números?
b) Entre los números –7, 8, 3, –10, 6, 4 y –2, ¿cuál es el más alejado de cero en la recta numérica? ¿Cuál está más cerca de cero en la recta numérica?
c) ¿Cuántos números enteros hay entre 21.000 y 1.000?
5. Representa cada conjunto de números enteros en la recta numérica.
a) A = {–5, 4, –3, 0, 7}
b) B = {–2, 6, 3, –1, –4}
c) C = {1, –7, 5, 4, –6, –3, –9, 7}
d) D = {–8, 5, –6, –4, 2, 1, 8, –9, –3, –1}
6. Escribe >, <, o = según corresponda.
a) –|8|________|–8|
b) –15_______–18
c) –|8|______–|–8|
d) –15_______18
e) –(–10)________|–10|
f) –(–12)________–12
1.3 Adición y sustracción en 

La adición de números enteros se puede representar en la recta numérica. Para ello, se ubica uno de los sumandos y se marca con un punto (•), luego se avanza a la derecha o a la izquierda tantas unidades como indique el otro sumando, según sea positivo (+) o negativo (–), respectivamente.
Actividades resueltas
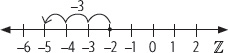
1. Representa la adición (–2) + (–3) en la recta numérica.
Se ubica el –2 en la recta numérica.
Se avanza tres unidades a la izquierda del –2.
Finalmente, se tiene que (–2) + (–3) = –5.
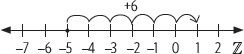
2. Representa la adición (–5) + 6 en la recta numérica.
Se ubica el –5 en la recta numérica.
Se avanza seis unidades a la derecha del –5.
Finalmente, se tiene que (–5) + 6 = 1.

Para resolver una adición de números enteros, sin usar una recta numérica, se deben tener en cuenta los siguientes casos:
Adición de dos números enteros con el mismo signo Adición de dos números enteros con distinto signo En este caso, se suman los valores absolutos de los números y al resultado se le antepone el signo común de los sumandos. En este caso, se resta al valor absoluto mayor el valor absoluto menor y al resultado se le antepone el signo del sumando que tiene mayor valor absoluto.Actividades resueltas
1. Calcula (–12) + (–17).
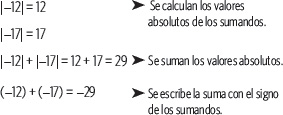
2. Calcula (–19) + 13.
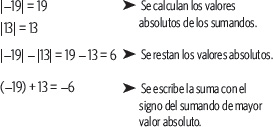

El inverso aditivo de un número entero a es un número entero b tal que a + b = 0, o sea, el inverso aditivo de a es –a. Un número entero y su inverso aditivo están a la misma distancia del cero en la recta numérica, pero tienen distinto signo. Para resolver una sustracción en

a – b = a + (–b)
Actividad resuelta
Resuelve el siguiente problema.
El matemático griego Euclides falleció aproximadamente en el año 265 a. C. y el matemático hindú Brahmagupta nació en el año 598 d. C. ¿Cuántos años de diferencia hay entre estos dos hechos?
Resolución:
Se resuelve la sustracción entre 598 y –265 de la siguiente manera:

Respuesta: Hay 863 años de diferencia entre el año en que nació Brahmagupta y el que falleció Euclides.
Actividades
1. Responde las siguientes preguntas.
a) ¿Cuál es el signo de la suma de dos números enteros negativos?
b) ¿Cuál es el signo de la suma de dos números enteros con signos diferentes?
c) ¿Cuál es el resultado de sumar un número entero con su inverso aditivo?
d) ¿Cuál es la diferencia entre un número entero y su inverso aditivo?
e) Si a la suma de dos números enteros se le resta la suma de sus inversos aditivos, ¿cuál es el resultado?
2. Resuelve.
a) (–13) + (–7)
b) (–17) + (–6)
c) (–9) + 15
d) (–21) + 12
e) 18 – (–21)
f) –8 – (–19)
g) 4 – (–10)
h) (–14) – 17
3. Determina en cada caso si la afirmación es verdadera o falsa. Justifica tu respuesta.



