The Way To Geometry

The seventh is thus. The angle eao, is lesser than a right-angle: Because it is part of a right angle, to wit of the outter angle, if ia, be drawne out at length.

And thus much of the angles of a circle, of all which the most effectuall and of greater power and use is the angle in a semicircle, and therefore it is not without cause so often mentioned of Aristotle. This Geometry therefore of Aristotle, let us somewhat more fully open and declare. For from hence doe arise many things.

Therefore

22 If two right lines jointly bounded with the diameter of a circle, be jointly bounded in the periphery, they doe make a right angle.

Or thus; If two right lines, having the same termes with the diameter, be joyned together in one point, of the circomference, they make a right angle. H.

This corollary is drawne out of the first part of the former Element, where it was said, that an angle in a semicircle is a right angle.

And

23 If an infinite right line be cut of a periphery of an externall center, in a point assigned and contingent, and the diameter be drawne from the contingent point, a right line from the point assigned knitting it with the diameter, shall be perpendicular unto the infinite line given.

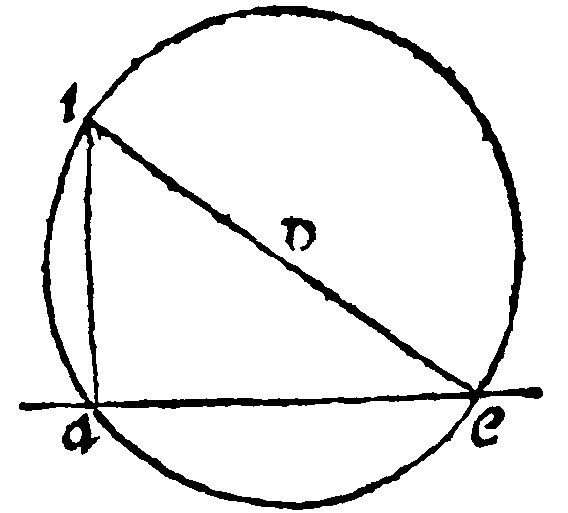
Let the infinite right line be ae, from whose point a, a perpendicular is to be raised.

The right line ae, let it be cut by the periphery aei, (whose center o, is out of the assigned ae,) and that in the point a, and a contingent point, as in e: And from e, let the diamiter be eoi: The right line ai, from a, the point given, knitting it with the diameter ioe, shall be perpendicular upon the infinite line ae; Because with the said infinite, it maketh an angle in a semicircle.

And

24 If a right line from a point given, making an acute angle with an infinite line, be made the diameter of a periphery cutting the infinite, a right line from the point assigned knitting the segment, shall be perpendicular upon the infinite line.

As in the same example, having an externall point given, let a perpendicular unto the infinite right line ae be sought: Let the right line ioe, be made the diameter of the peripherie; and withall let it make with the infinite right line given an acute angle in e, from whose bisection for the center, let a periphery cut the infinite, &c.

And

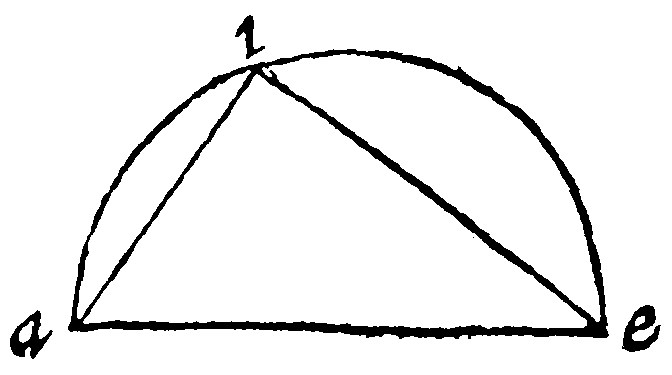
25 If of two right lines, the greater be made the diameter of a circle, and the lesser jointly bounded with the greater and inscribed, be knit together, the power of the greater shall be more than the power of the lesser by the quadrate of that which knitteth them both together. ad 13 p. x.

As in this example; The power of the diameter ae, is greater than the power of ei, by the quadrate of ai. For the triangle aei, shall be a rectangle; And by the 9 e xij. ae, the greater shall be of power equall to the shankes. Out of an angle in a semicircle Euclide raiseth two notable fabrickes; to wit, the invention of a meane proportionall betweene two lines given: And the Reason or rate in opposite sections. The genesis or invention of the meane proportionall, of which we heard at the 9 e viij. is thus:

26 If a right line continued or continually made of two right lines given, be made the diameter of a circle, the perpendicular from the point of their continuation unto the periphery, shall be the meane proportionall betweene the two lines given. 13 p vj.

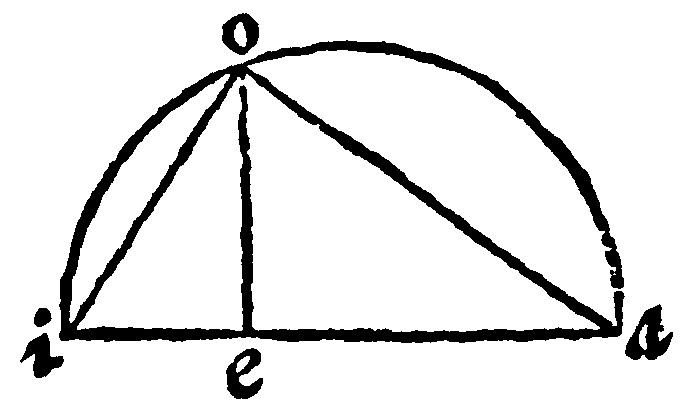
As for example, let the assigned right lines be ae, and ei, of the which aei, is continued. And let eo, be perpendicular from the periphery aoi, unto e, the point of continuation or joyning together of the lines given. This eo, say I, shall be the meane proportionall: Because drawing the right lines ao, and io, you shall make a rectangled triangle, seeing that aoi, is an angle in a semicircle: And, by the 9 e viij. oe, shall be proportionall betweene ae, and ei.

So if the side of a quadrate of 10. foote content, were sought; let the sides 1. foote and 10. foote an oblong equall to that same quadrate, be continued; the meane proportionall shall be the side of the quadrate, that is, the power of it shall be 10. foote. The reason of the angles in opposite sections doth follow.

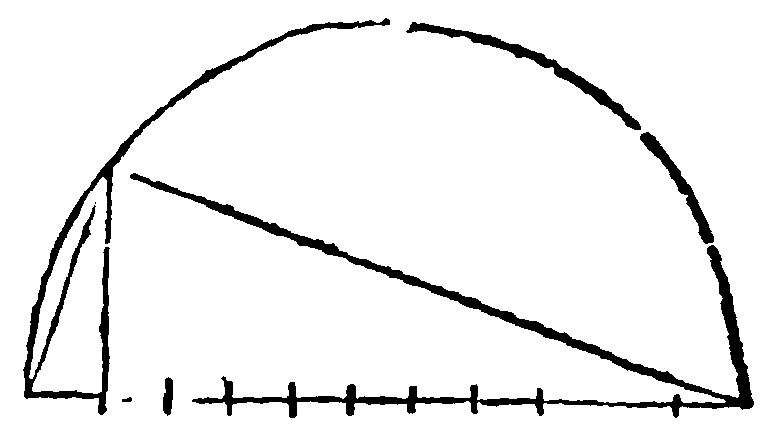
27 The angles in opposite sections are equall in the alterne angles made of the secant and touch line. 32. p iij.

If the sections be equall or alike, then are they the sections of a semicircle, and the matter is plaine by the 21 e. But if they be unequall or unlike the argument of demonstration is indeed fetch'd from the angle in a semicircle, but by the equall or like angle of the tangent and end of the diameter.

As let the unequall sections be eio, and eao: the tangent let it be uey: And the angles in the opposite sections, eao, and eio. I say they are equall in the alterne angles of the secant and touch line oey, and oeu. First that which is at a, is equall to the alterne oey: Because also three angles oey, oea, and aeu, are equall to two right angles, by the 14 e v. Unto which also are equall the three angles in the triangle aeo, by the 13 e vj. From three equals take away the two right angles aue, and aoe: (For aoe, is a right angle, by the 21 e; because it is in a semicircle:) Take away also the common angle aeo: And the remainders eao, and oey, alterne angles, shall be equall.

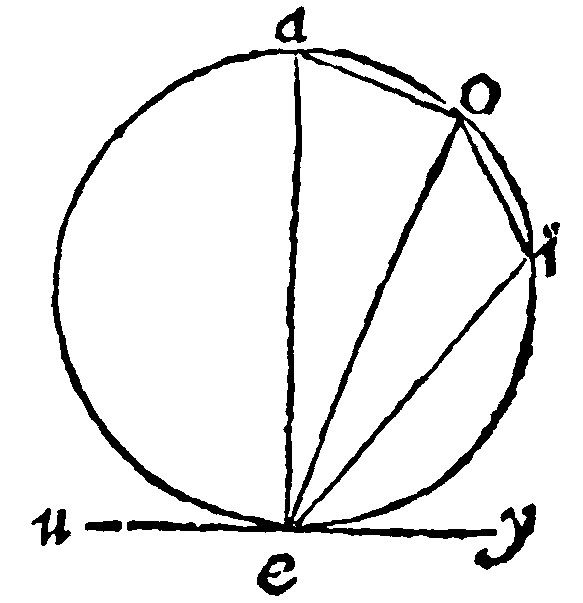
Secondarily, the angles at a, and i, are equall to two right angles, by the 14, e: To these are equall both oey, and oeu. But eao, is equall to the alterne oey. Therefore that which is at i, is equall to, the other alterne oeu. Neither is it any matter, whether the angle at a, be at the diameter or not: For that is onely assumed for demonstrations sake: For wheresoever it is, it is equall, to wit, in the same section. And from hence is the making of a like section, by giving a right line to be subtended.

Therefore

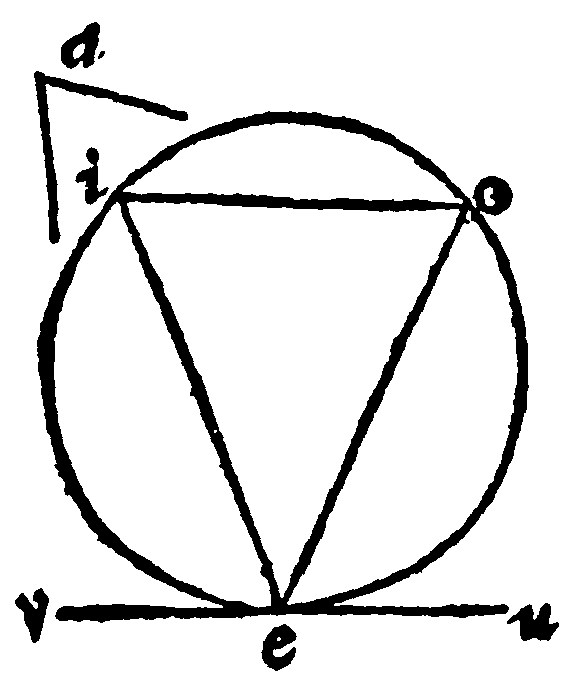
28 If at the end of a right line given a right lined angle be made equall to an angle given, and from the toppe of the angle now made, a perpendicular unto the other side do meete with a perpendicular drawn from the middest of the line given, the meeting shall be the center of the circle described by the equalled angle, in whose opposite section the angle upon the line given shall be made equall to the assigned è 33 p iij.

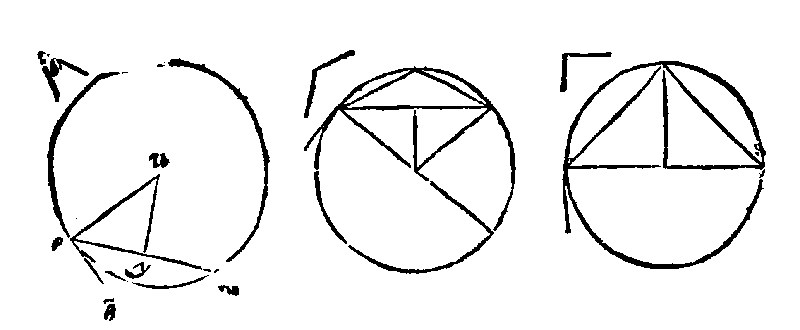
This you may make triall of in the three kindes of angles, all wayes by the same argument: as here the angle given is a: The right line given ei: at the end e, the equalled angle, ieo: The perpendicular to the side eo, let it be eu: But from the middest of the line given let it be yu. Here u, shall be the center desired. And from hence one may make a section upon a right line given, which shall receive a rectilineall angle equall to an angle assigned.

And

29 If the angle of the secant and touch line be equall to an assigned rectilineall angle, the angle in the opposite section shall likewise be equall to the same. 34. p iij.

As in this figure underneath. And from hence one may from a circle given cut off a section, in which there is an angle equall to the assigned. As let the angle given be a: And the circle eio. Thou must make at the point e, of the secant eo, and the tangent yu, an angle equall to the assigned, by the 11 e iij. such as here is oeu: Then the section oei, shall containe an angle equall to the assigned.

Of Geometry the seventeenth Booke, Of the Adscription of a Circle and Triangle

Hitherto we have spoken of the Geometry of Rectilineall plaines, and of a circle: Now followeth the Adscription of both: This was generally defined in the first book 12 e. Now the periphery of a circle is the bound therof. Therefore a rectilineall is inscribed into a circle, when the periphery doth touch the angles of it 3 d iiij. It is circumscribed when it is touched of every side by the periphery; 4 d iij.

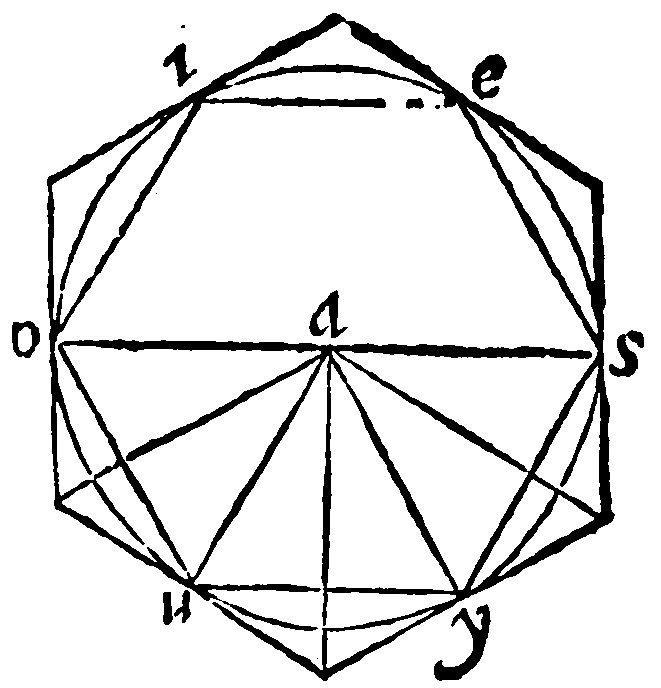
1. If rectilineall ascribed unto a circle be an equilater, it is equiangle.

Of the inscript it is manifest; And that of a Triangle by it selfe: Because if it be equilater, it is equiangle, by the 19 e vj. But in a Triangulate the matter is to be prooved by demonstration. As here, if the inscripts ou, and sy, be equall, then doe they subtend equall peripheries, by the 32 e xv. Then if you doe omit the periphery in the middest betweene them both, as here uy, and shalt adde oies the remainder to each of them, the whole oiesy, subtended to the angle at u: And uoies, subtended to the angle at y, shall be equall. Therefore the angles in the periphery, insisting upon equall peripheries are equall.

Of the circumscript it is likewise true, if the circumscript be understood to be a circle. For the perpendiculars from the center a, unto the sides of the circumscript, by the 9 e xij, shal make triangles on each side equilaters, & equiangls, by drawing the semidiameters unto the corners, as in the same exāple.

2. It is equall to a triangle of equall base to the perimeter, but of heighth to the perpendicular from the center to the side.

As here is manifest, by the 8 e vij. For there are in one triangle, three triangles of equall heighth.

The same will fall out in a Triangulate, as here in a quadrate: For here shal be made foure triangles of equall height.

Lastly every equilater rectilineall ascribed to a circle, shall be equall to a triangle, of base equall to the perimeter of the adscript. Because the perimeter conteineth the bases of the triangles, into the which the rectilineall is resolved.

3. Like rectilinealls inscribed into circles, are one to another as the quadrates of their diameters, 1 p. xij.

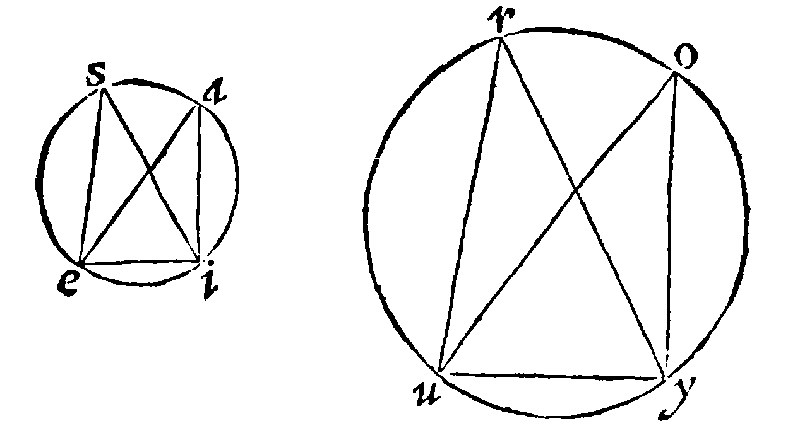
Because by the 1 e vj, like plains have a doubled reasó of their homologall sides. But in rectilineals inscribed the diameters are the homologall sides, or they are proportionall to their homologall sides. As let the like rectangled triangles be aei, and ouy; Here because ae and ou, are the diameters, the matter appeareth to be plaine at the first sight. But in the Obliquangled triangles, sei, and ruy, alike also, the diameters are proportionall to their homologall sides, to wit, ei and uy. For by the grant, as se is to ru: so is ei to uy, And therefore, by the former, as the diameter ea and uo.

In like Triangulates, seeing by the 4 e x, they may be resolved into like triangles, the same will fall out.

Therefore

4. If it be as the diameter of the circle is unto the side of rectilineall inscribed, so the diameter of the second circle be unto the side of the second rectilineall inscribed, and the severall triangles of the inscripts be alike and likely situate, the rectilinealls inscribed shall be alike and likely situate.

This Euclide did thus assume at the 2 p xij, and indeed as it seemeth out of the 18 p vj. Both which are conteined in the 23 e iiij. And therefore we also have assumed it.

Adscription of a Circle is with any triangle: But with a triangulate it is with that onely which is ordinate: And indeed adscription of a Circle is common to all.

5. If two right lines doe cut into two equall parts two angles of an assigned rectilineall, the circle of the ray from their meeting perpendicular unto the side, shall be inscribed unto the assigned rectilineall. 4 and 8. p. iiij.

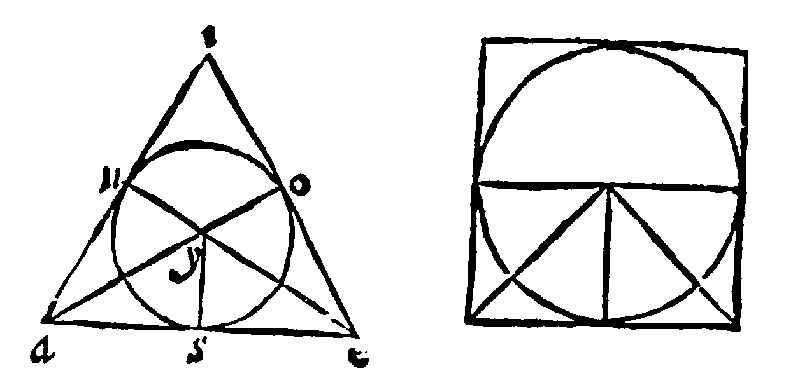
As in the Triangle aei, let the right lines ao, and eu, halfe the angles a and e: And from y, their meeting, let the perpendiculars unto the sides be yo, yu, ys; I say that the center y, with the ray yo, or ya, or ys, is the circle inscribed, by the 17 e xv. Because the halfing lines with the perpendiculars shall make equilater triangles, by the 2 e vij. And therefore the three perpendiculars, which are the bases of the equilaters, shall be equall.

The same argument shall serve in a Triangulate.

6. If two right lines do right anglewise cut into two equall parts two sides of an assigned rectilineall, the circle of the ray from their meeting unto the angle, shall be circumscribed unto the assigned rectilineall. 5 p iiij.

As in former figures. The demonstration is the same with the former. For the three rayes, by the 2 e vij, are equall: And the meeting of them, by the 17 e x, is the center.

And thus is the common adscription of a circle: The adscription of a rectilineall followeth, and first of a Triangle.

7. If two inscripts, from the touch point of a right line and a periphery, doe make two angles on each side equall to two angles of the triangle assigned be knit together, they shall inscribe a triangle into the circle given, equiangular to the triangle given è 2 p iiij.

Let the Triangle aei be given: And the circle, o, into which a Triangle equiangular to the triangle given, is to be inscribed. Therefore let the right line uys, touch the periphery yrl: And from the touch y, let the inscripts yr, and yl, make with the tangent two angles uyr, and syl, equall to the assigned angles aei, and aie: And let them be knit together with the right line rl: They shall by the 27 e xvj, make the angle of the alterne segments equall to the angles uyr, and syl. Therefore by the 4 e vij seeing that two are equall, the other must needs be equall to the remainder.

The circumscription here is also speciall.

8 If two angles in the center of a circle given, be equall at a common ray to the outter angles of a triangle given, right lines touching a periphery in the shankes of the angles, shall circumscribe a triangle about the circle given like to the triangle given. 3 p iiij.

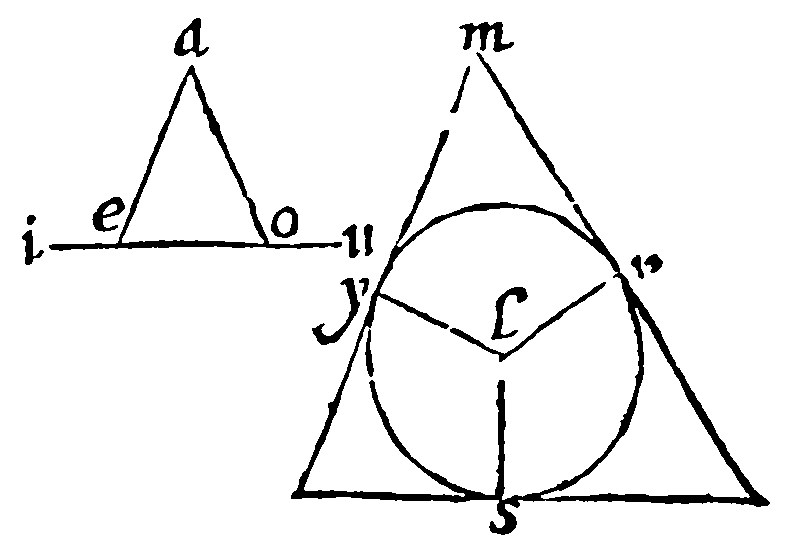
Let there be a Triangle, and in it the outter angles aei, and aou: The Circle let it be ysr; And in the center l, let the angles ylr, and slr; at the common side lr, bee made equall to the said outter angles aei, and aou. I say the angles of the circumscribed triangle, are equall to the angles of the triangle given. For the foure inner angles of the quadrangle ylrm, are equall to the foure right angles, by the 6 e x: And two of them, to wit, at y and r, are right angles, by the construction: For they are made by the secant and touch line, from the touch point by the center, by the 20 e xv. Therefore the remainders at l and m, are equall to two right angles: To which two aei and aeo are equall. But the angle at l, is equall to the outter: Therefore the remainder m, is equall to aeo. The same shall be sayd of the angles aoe, and aou. Therefore two being equall, the rest at a and i, shall be equall.

Therefore

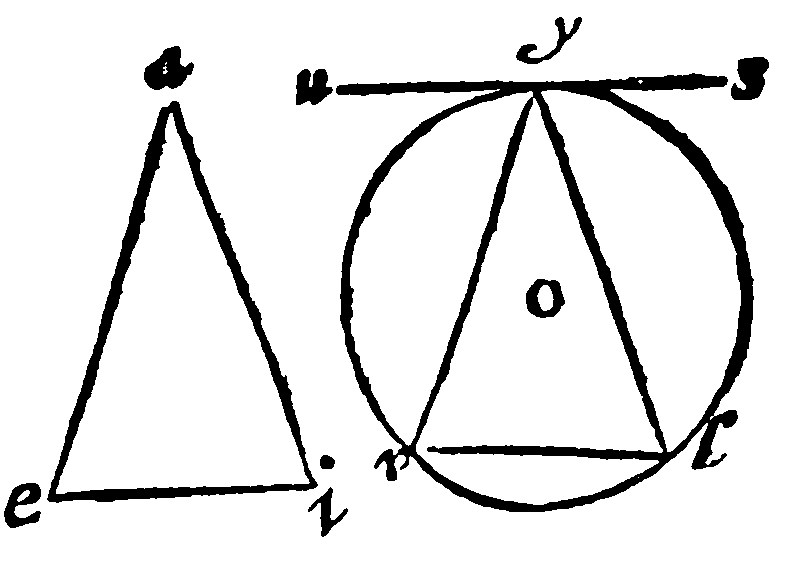
9. If a triangle be a rectangle, an obtusangle, an acute angle, the center of the circumscribed triangle is in the side, out of the sides, and within the sides: And contrariwise. 5 e iiij.

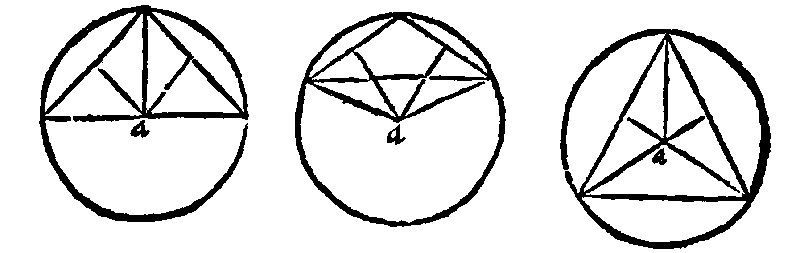
As, thou seest in these three figures, underneath, the center a.

Of Geometry, the eighteenth Booke, Of the adscription of a Triangulate

Such is the Adscription of a triangle: The adscription of an ordinate triangulate is now to be taught. And first the common adscription, and yet out of the former adscription, after this manner.

1. If right lines doe touch a periphery in the angles of the inscript ordinate triangulate, they shall onto a circle cirumscribe a triangulate homogeneall to the inscribed triangulate.

The examples shall be laid downe according as the species or severall kindes doe come in order. The speciall inscription therefore shall first be taught, and that by one side, which reiterated, as oft as need shall require, may fill up the whole periphery. For that Euclide did in the quindecangle one of the kindes, we will doe it in all the rest.

2. If the diameters doe cut one another right-angle-wise, a right line subtended or drawne against the right angle, shall be the side of the quadrate. è 6 p iiij.

As here. For the shankes of the angle are the raies whose diameters knit together shall make foure rectangled triangles, equall in shankes: And by the 2 e vij, equall in bases. Therefore they they shall inscribe a quadrate.

Therefore

3. A quadrate inscribed is the halfe of that which is circumscribed.

Because the side of the circumscribed (which here is equall to the diameter of the circle) is of power double, to the side of the inscript, by the 9 e xij.

And

4. It is greater than the halfe of the circumscribed Circle.

Because the circumscribed quadrate, which is his double, is greater than the whole circle.

For the inscribing or other multangled odde-sided figures we must needes use the helpe of a triangle, each of whose angles at the base is manifold to the other: In a Quinquangle first, that which is double unto the remainder, which is thus found.

5. If a right line be cut proportionally, the base of that triangle whose shankes shall be equall to the whole line cut, and the base to the greater segment of the same, shall have each of the angles at base double to the remainder: And the base shall be the side of the quinquangle inscribed with the triangle into a circle. 10, and 11. p iiij.

Here first thou shalt take for the fabricke or making of the Triangle, for the ray the right line ae by the 3 e xiiij, cut proportionally in o: A circle also shalt thou make upon the center a, with the ray ae: And then shalt thou by the 6 e xv, inscribe a right line equall to the greater segment: And shalt knit the same inscript with the whole line cut with another right line. This triangle shall be your desire. For by the 17 e vj, the angles at the base ei are equall, so that looke whatsoever is prooved of the one, is by and by also prooved of the other. Then let oi be drawne; And a Circle, by the 8 e xvij, circumscribed about the triangle aoi. This circle the right line ei, shall touch, by the 27 e xv. Because, by the grant, the right line ae, is cut proportionally, therefore the Oblong of the secant and outter segment, is equall to the quadrate of the greater segment, to which by the grant, the base ei, is equall. Here therefore the angle aie is the double of the angle at a: because it is equall to the angles aio, and oai, which are equall betweene themselves. For by the 27 e xvj it is equall to the angle oai in the alterne segment. And the remainder aio, is equall to it selfe. Therefore also the angle aei, is equall to the same two angles, because it is equall to the angle aie. But the outter angle eoi, is equall to the same two, by the 15 e vj. Therefore the angles ioe and oei (because they are equall to the same) they are equall betweene themselves. Wherefore by the 17 e vj, the sides oi and ei are equall. And there also ao and oi: And the angles oai & oia are equall by the 17 e vj. Wherefore seeing that to both the angle aie is equall, it shall be the double of either of the equalls.

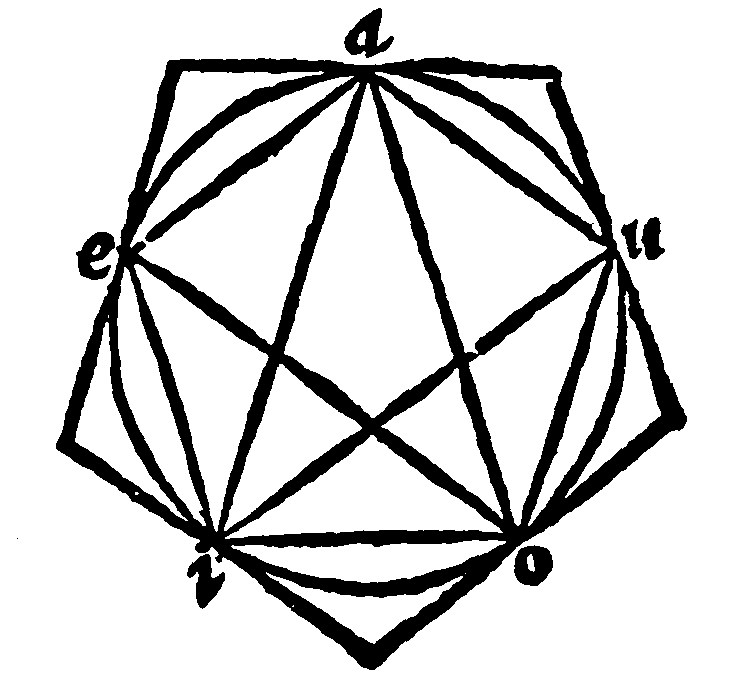
But the base ei, is the side of the equilater quinquangle. For if two right lines halfing both the angles of a triangle which is the double of the remainder, be knit together with a right line, both one to another, and with the angles, shall inscribe unto a circle an equilater triangle, whose one side shall be the base it selfe: As here seeing the angles eoa, eoi, uio, uia, iao, are equal in the periphery, the peripheries, by the 7 e, xvj. subtending them are equall: And therefore, by the 32 e, xv. the subtenses ae, ei, io, ou, ua, are also equall. Now of those five, one is ae. Therefore a right line proportionall cut, doth thus make the adscription of a quinquangle: And from thence againe is afforded a line proportionally cut.

6 If two right lines doe subtend on each side two angles of an inscript quinquangle, they are cut proportionally, and the greater segments are the sides of the said inscript è 8, p xiij.

As here, Let ai, and eu, subtending the angles on each side aei, and eau: I say, That they are proportionally cut in the point s: And the greater segments si, and su, are equall to ae, the side of the quinquangle. For here two triangles are equiangles: First aei, and uae, are equall by the grant, and by the 2 e, vij. Therefore the angles aie, and aes, are equall. Then aei, and ase, are equall: Because the angle at a, is common to both: Therefore the other is equall to the remainder, by the 4 e, 7. Now, by the 12. e, vij. as ia, is unto ae, that is, as by and by shall appeare, unto is: so is ea, unto as: Therefore, by the 1 e, xiiij. ia, is cut proportionally in s. But the side ea, is equall to is: Because both of them is equall to the side ei, that by the grant, this by the 17. e, vj. For the angles at the base, ise, and ies, are equall, as being indeed the doubles of the same. For ise, by the 16. e vj. is equall to the two inner, which are equall to the angle at u, by the 17 e vj. and by the former conclusion. Therefore it is the double of the angles aes: Whose double also is the angle uei, by the 7 e. xvj. insisting indeede upon a double periphery.