The Way To Geometry

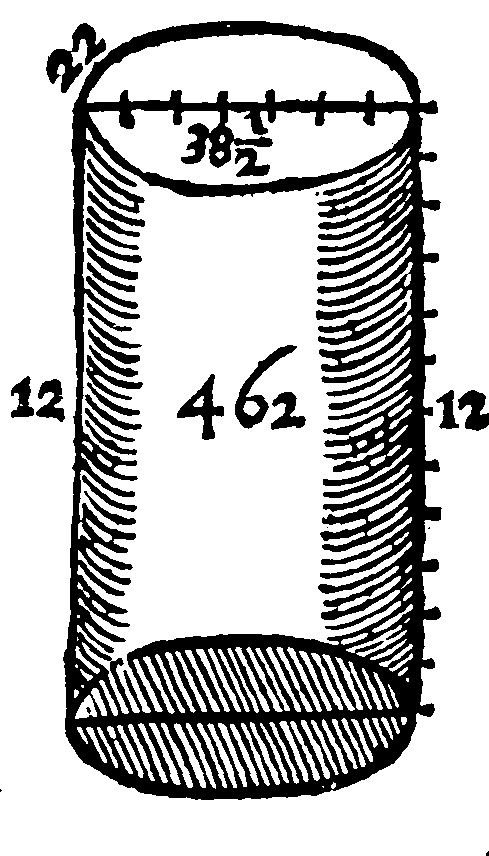
17 A cylinderlike forme is that which from the periphery underneath unto the the upper one, equall and parallell unto it, is equally raised.

Therefore

18 It is made by the turning of the side about two equall and parallell peripheries.

19 The plaine of his side and heighth is the cylinderlike surface.

As here the periphery is 22. as is gathered by the Diameter, which is 7. The heighth is 12. The base therefore is 38.1/2. And 38.1/2 by 12. are 462. for the cylinderlike surface. To which if you shall adde both the bases on each side, to wit, 38.1/2. twise, or 77. once, the whole surface shall be 539.

Geometry, the one and twentieth Book, Of Lines and Surfaces in solids

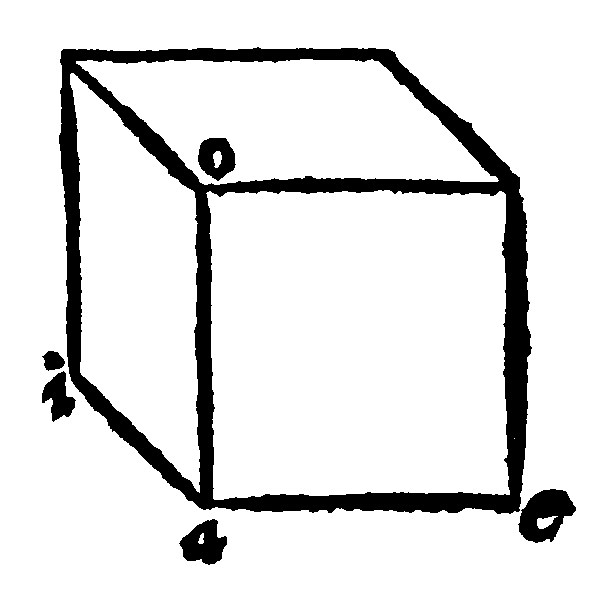
1 A body or solid is a lineate broad and high 1 d xj.

For length onely is proper to a line: Length and breadth, to a surface: Length breath, and heighth joyntly, belong unto a body: This threefold perfection of a magnitude, is proper to a body: Whereby wee doe understand that are in a body, not onely lines of length, and surfaces of breadth, (for so a body should consist of lines and surfaces.) But we do conceive a solidity in length, breadth and heighth. For every part of a body is also a body. And therefore a solid we doe understand the body it selfe. As in the body aeio, the length is ae; the breadth, ai, And the heighth, ao.

2 The bound of a solid is a surface 2 d xj.

The bound of a line is a point: and yet neither is a point a line, or any part of a line. The bound of a surface is a line: And yet a line is not a surface, or any part of a surface. So now the bound of a body is a surface: And yet a surface is not a body, or any part of a body. A magnitude is one thing; a bound of a magnitude is another thing, as appeared at the 5 e j.

As they were called plaine lines, which are conceived to be in a plaine, so those are named solid both lines and surfaces which are considered in a solid; And their perpendicle and parallelisme are hither to be recalled from simple lines.

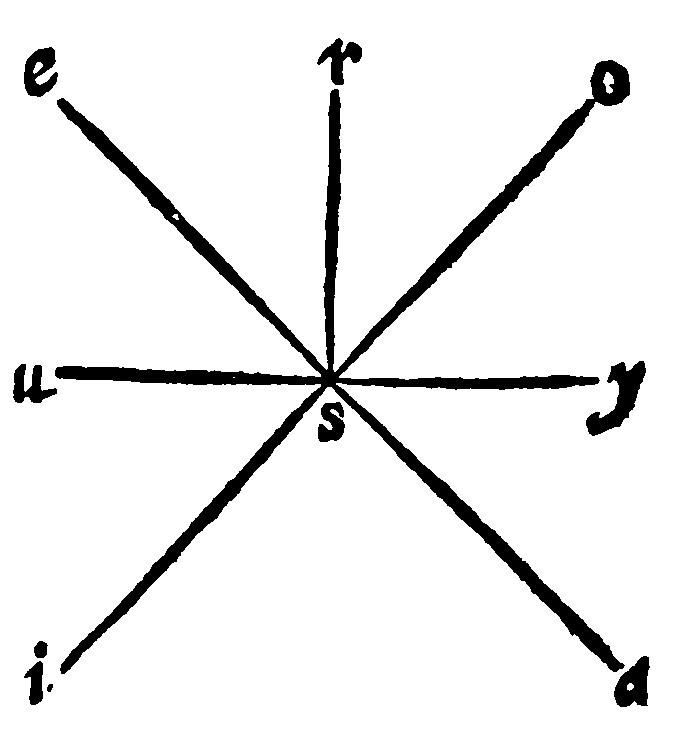
3 If a right line be unto right lines cut in a plaine underneath, perpendicular in the common intersection, it is perpendicular to the plaine beneath: And if it be perpendicular, it is unto right lines, cut in the same plaine, perpendicular in the common intersection è 3 d and 4 p xj.

Perpendicularity was in the former attributed to lines considered in a surface. Therefore from thence is repeated this consectary of the perpendicle of a line with the surface it selfe.

If thou shalt conceive the right lines, ae, io, uy, to cut one another in the plaine beneath, in the common intersections: And the line rs, falling from above, to be to every one of them perpendicular in the common point s, thou hast an example of this consectary.

4 If three right lines cutting one another, be unto the same right line perpendicular in the common section, they are in the same plaine 5. p xj.

For by the perpendicle and common section is understood an equall state on all parts, and therefore the same plaine: as in the former example, as, ys, os, suppose them to be to sr, the same loftie line, perpendicular, they shall be in the same nearer plaine aiueoy.

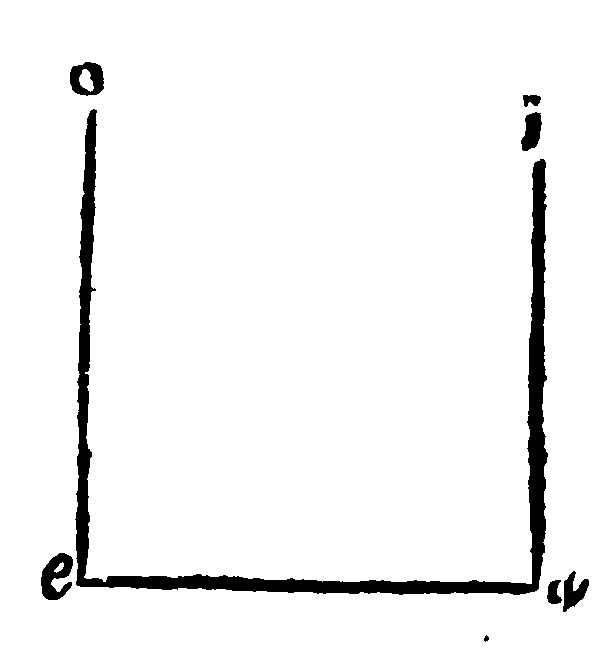
5 If two right lines be perpendicular to the under-plaine, they are parallells: And if the one two parallells be perpendicular to the under plaine, the other is also perpendicular to the same. 6. 8 p xj.

The cause is out of the first law or rule parallells. For if two right lines be perpendicular to the same under plaine, being joyned together by a right line, they shall make their inner corners equall to two right angles: And therefore they shall be parallells, by the 21. e v. And if in two parallells knit together with a right line, one of the inner angles, be a right angle: the other also shall be a right angle. Because they are divided by a common perpendicular; As in the example. If the angles at a, and e, be right angles, ai, and eo, are parallells, and contrariwise, if ai, and eo be parallells, and the angle at a, be a right angle, the angle at e, also shall be a right angle.

6 If right lines in diverse plaines be unto the same right line parallel, they are also parallell betweene themselves. 9 p xj.

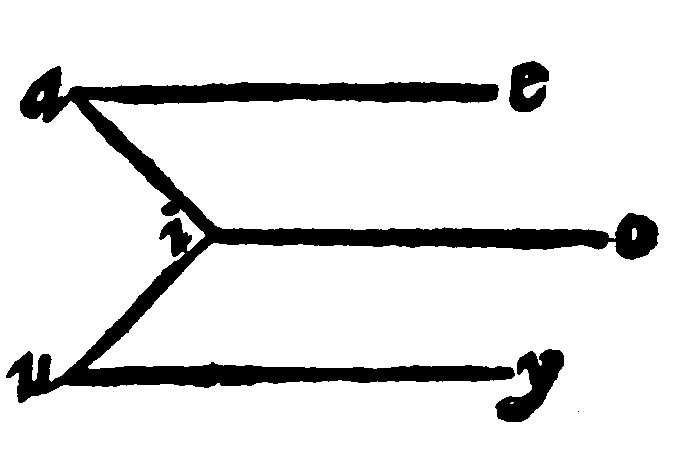
As here ae, and uy, right lines in diverse plaines suppose them to be parallell to io: I say, they are parallell one to another. For from the point i, let ia, and iu, be erected at right angles to io to cut the parallells, by the 17. e v. Therefore, by the 3 e, oi, seeing that it is perpedicular to ia, and iu, two lines cutting one another, it is perpendicular to the plaine beneath. Therefore by the the 6 e, yu, and ea, are perpendicular to the same plaine: And therefore, by the same, they are parallell.

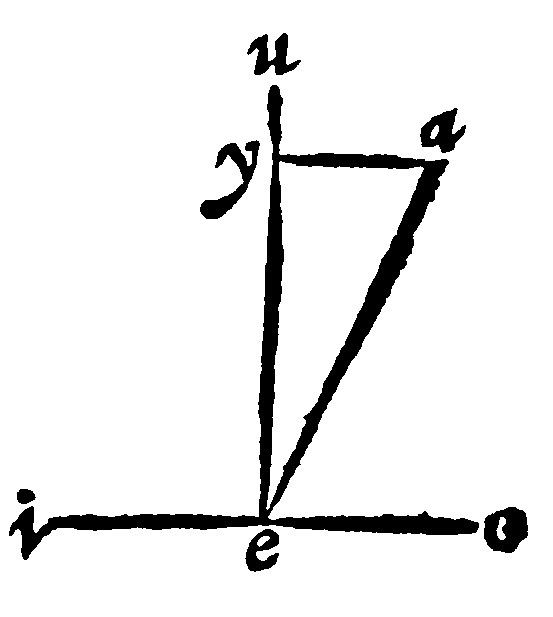
7 If two right lines be perpendiculars, the first from a point above, unto a right line underneath, the second from the common section in the plaine underneath, a third, from the sayd point perpendicular to the second, shall be perpendicular to the plaine beneath. è 11 p xj.

It is a consectary out of the 3 e. As for example, if from a lofty point a, ae, be by the 18 e v, perpendicular to e, a point of the right line io underneath: And from e the common section, by the 17 e v, there be eu, another perpendicular: Lastly ay, a lofty right line, be by the 18 e v, perpendicular unto eu, at the point y, ay shall be perpendicular unto the plaine underneath. For that ae is perpendicular to io, the same ae declineth neither to the right hand, nor to the left, by the 13 e ij. And in that againe ay is perpendicular to eu, it leaneth neither forward nor backeward. Therefore it lyeth equally or indifferently, betweene the foure quarters of the world.

If the right line io, doe with equall angles agree to r, the third element.

8. If a right line from a point assigned of a plaine underneath, be parallell to a right line perpendicular to the same plaine, it shall also be perpendicular to the plaine underneath. ex 12 p xj.

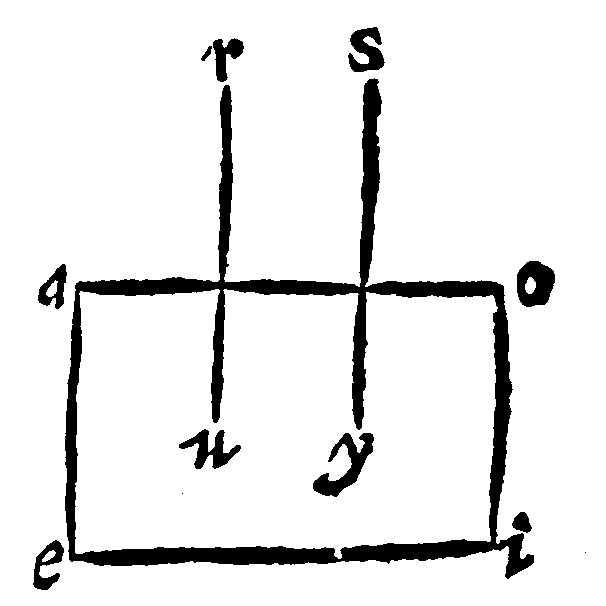
As for example let the plaine be aeio: And the assigned point in it u: From this point a lofty perpendicular is to be erected. Let there be made from the point y, the perpendicular ys, unto the plaine underneath, by the 7 e. And to it let ur, be made parallell by the 24 e v. Now ur, seeing it is parallell to a perpendicular upon the plaine underneath, it shall be perpendicular to the same, by the 5 e.

9. If a right line in one of the plaines cut, perpendicular to the common section, be perpendicular to the other, the plaines are perpendicular: And if the plaines be perpendicular, a right line in the one perpendicular to the common section is perpendicular to the other è 4 d, and 38 p xj.

The perpendicularity of plaines, is drawne out of the former condition of the perpendicle: And the state of plaines on each side equall betweene themselves, is fetch'd from a perpendicularity of a right line falling upon a plaine. Because from hence it is understood that the plaine it selfe doth lye indifferently betweene all parts signified by right lines: Which in a Booke with the pages each way opened, is perceived by the verses or lines of the pages, both to the section and plaine underneath, perpendicular as here thou seest.

10. If a right line be perpendicular to a plaine, all plaines by it, are perpendicular to the same: And if two plaines be unto any other plaine perpendiculars, the common section is perpendicular to the same. e 15, and 19 p. xj.

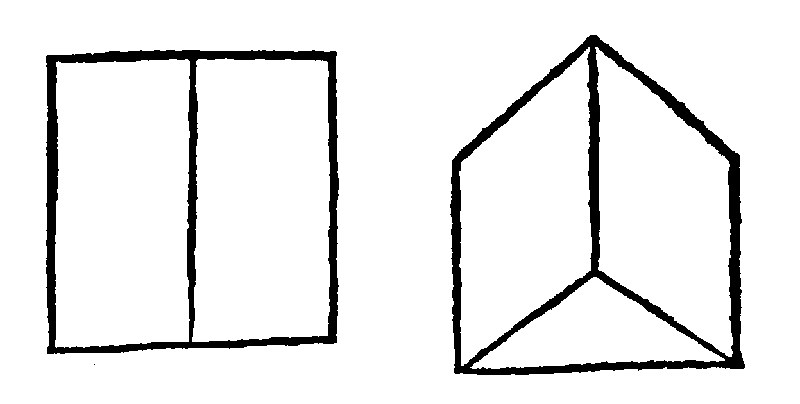
The first is a consectary drawne out of the 9 e. And the latter is from hence manifest, because that same common section is a right line, in any manner of lofty plaines intersected, perpendicular both to the common section and plaine underneath. For if the common section, were not perpendicular to the plaine underneath, neither should the plaines cutting one another be perpendicular to the plaine underneath, but some one should be oblique, against the grant, as here thou seest.

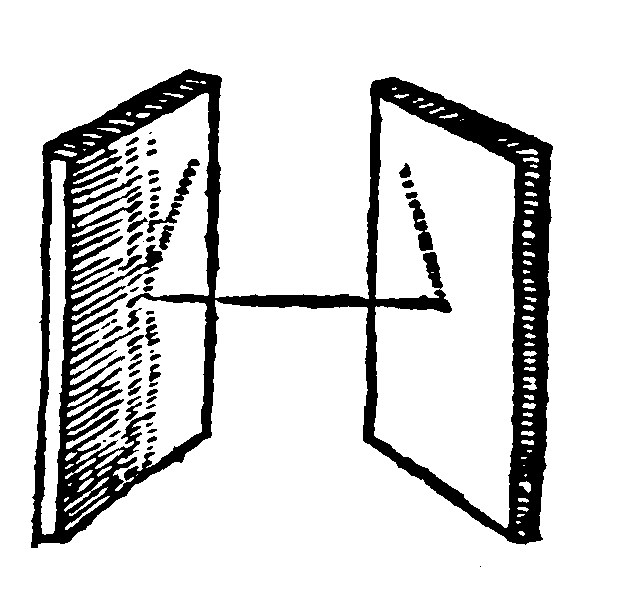
11. Plaines are parallell which doe leane no way. 8 d xj.

And

12. Those which divided by a common perpendicle. 14 p xj.

It is a consectary out of the 3, and 6 e. For if the middle right line be perpendicular to both the plaines, it is also to the right lines on either side cut, perpendicular in the common intersection: And the inner angles on each side, being right angles, will evince them to be parallels.

It is also out of the definition of parallels, at the 15 e ij.

And

13. If two paires of right in them be joyntly bounded, they are parallell. 15 p xj.

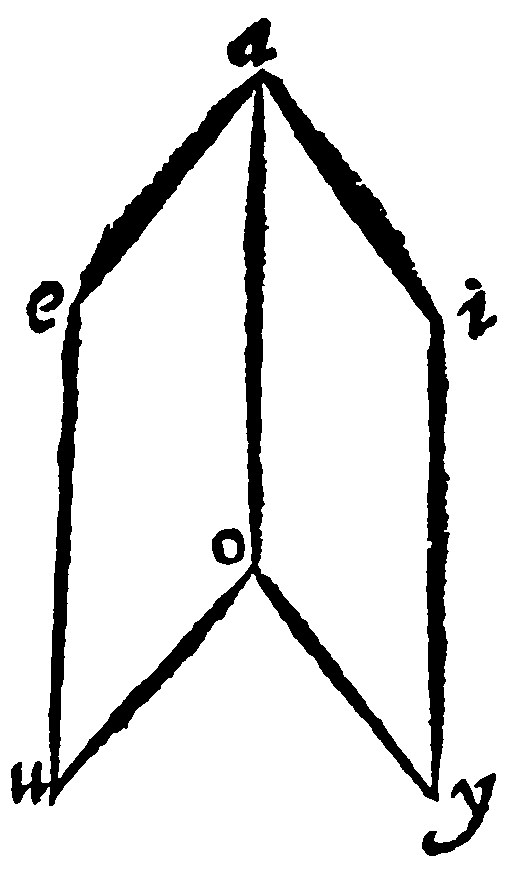
Such are the opposite walls in the toppe or ridge of houses. As let aei, and uoy, be plaine which have two payres of right lines, ea, and ia: Item uo, and yo, joyntly bounded in a, and o: And parallels, to wit ea, against uo: and ia, against yo. I say that the plaines themselves are parallels: For the right lines ue, and oa: item yi, and oa, doe knit together equall parallels, they shal by the 27 e v, be equall and parallels: And so they shall prove the equidistancie.

The same will fall out if thou shalt imagine the joyntly bounded to infinitely drawn out; for the plaines also infinitely extended shall be parallell.

14. If two parallell plaines are cut with another plaine, the common sections are parallels, 16 p xj.

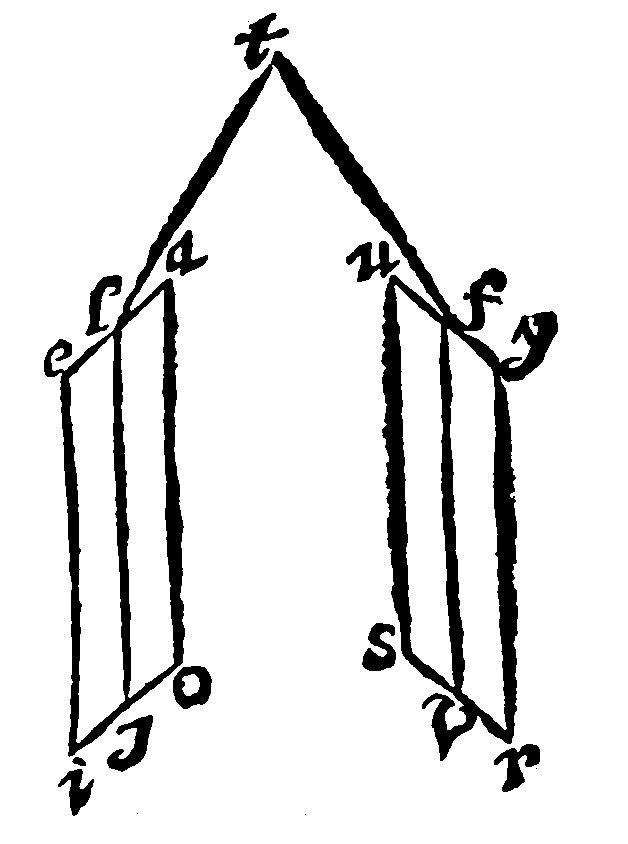
As here thou seest the parallell plaines aeio, and uysr, cut by the plaine ljvf, the common sections lj, and fv, shall also be parallell: Otherwise they themselves, and therefore also the plaines in which they are, shall meete, as in the point t, which is against the grant.

The twenty second Booke, of P. Ramus Geometry, Of a Pyramis

1. The axis of a solid is the diameter about which it is turned, e 15, 19, 22 d xj.

The Axis or Axeltree is commonly thought to be proper to the sphere or globe, as here ae: But it is attributed to other kindes of solids, as well as to that.

2. A right solid is that whose axis is perpendicular to the center of the base.

Thus Serenus and Apllonius doe define a Cone and a Cylinder: And these onely Euclide considered: Yea and indeed stereometry entertaineth no other kinde of solid but that which is right or perpendicular.

3. If solids be comprehended of homogeneall surfaces, equall in multitude and magnitude, they are equall. 10 d xj.

Equality of lines and surfaces was not informed by any peculiar rule; farther than out of reason and common sense, and in most places congruency and application was enough and did satisfie to the full: But here the congruency of Bodies is judged by their surfaces. Two cubes are equall, whose sixe sides or plaine surfaces, are equall, &c.

4. If solids be comprehended of surfaces in multitude equall and like, they are equall, 9 d xj.

This is a consectary drawne out of the general difinition of like figures, at the 19 e. iiij. For there like figures were defined to be equiangled and proportionall in the shankes of the equall angles: But in like plaine solids the angles are esteemed to be equall out of the similitude of their like plaines: And the equall shankes are the same plaine surfaces, and therefore they are proportionall, equall and alike.

5 Like solids have a treble reason of their homologall sides, and two meane proportionalls. 33. p xj. 8 p xij.

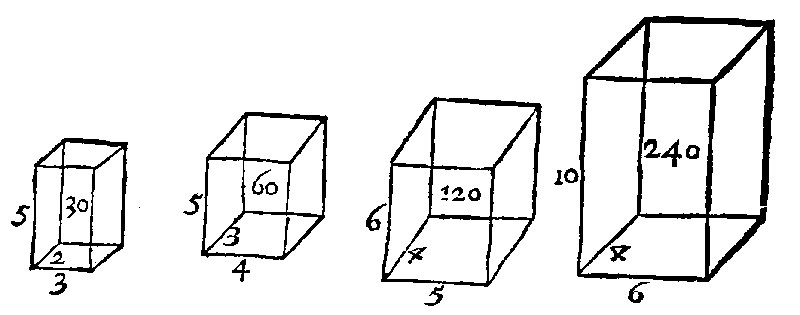
It is a consectary drawne out of the 24 e. iiij. as the example from thence repeated shall make manifest.

6 A solid is plaine or embosed.

7 A plaine solid is that which is comprehended of plaine surfaces.

8 The plaine angles comprehending a solid angle, are lesse than foure right angles. 21. p xj.

For if they should be equall to foure right angles, they would fill up a place by the 27 e, iiij. neither would they at all make an angle, much lesse therefore would they doe it if they were greater.

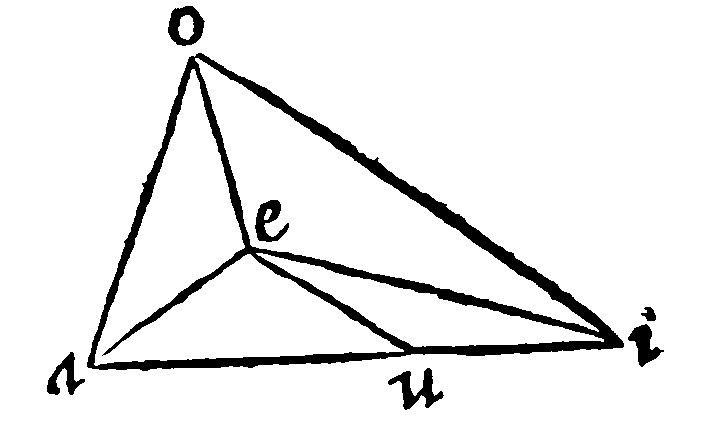
9 If three plaine angles lesse than foure right angles, do comprehend a solid angle, any two of them are greater than the other: And if any two of them be greater than the other, then may comprehend a solid angle, 21. and 23. p xj.

It is an analogy unto the 10 e vj. and the cause is in a readinesse. For if two plaine angles be equall to the remainder, they shall with that third include no space betweene them: But if thou shalt conceit to fit the plaine to the shankes, with the congruity they should of two make one: but much lesse if they be lesser.

The converse from hence also is manifest.

Euclide doth thus demonstrate it: First if three angles are equall, then by and by two are conceived to be greater than the remainder. But if they be unequall, let the angle aei, be greater than the angle aeo: And let aeu, equall to aeo, be cut off from the greater aei: And let eu, be equall to eo. Now by the 2 e, vij. two triangles aeu, and aeo, are equall in their bases au, and ao. Item ao, and ei, are greater than ai, and ao: And ao, is equall to au. Therefore oi, is greater than iu. Here two triangles, uei, and ieo, equall in two shankes; and the base oi, greater than the base iu. Therefore, by the 5 e vij. the angle oei, is greater than the angle ieu. Therefore two angles aeo, and oei, are greater than aei.

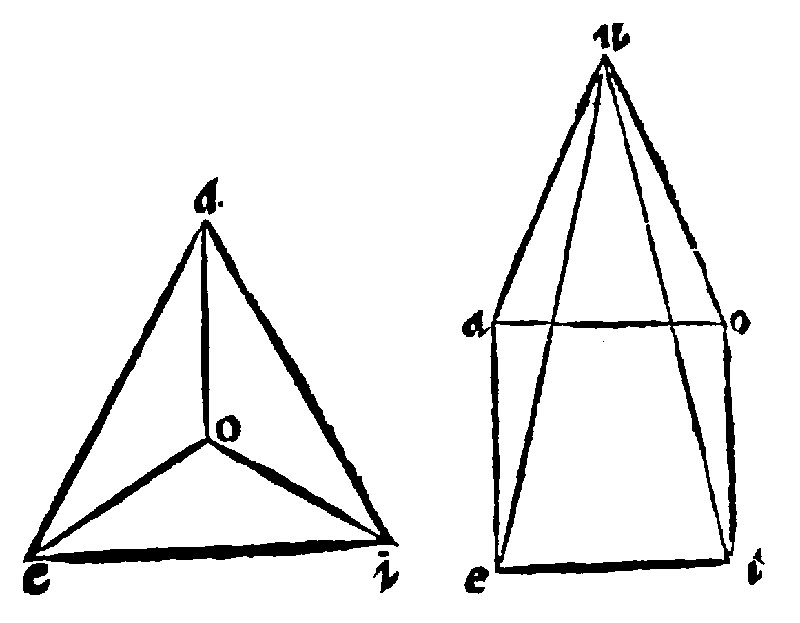
10 A plaine solid is a Pyramis or a Pyramidate.

11 A Pyramis is a plaine solid from a rectilineall base equally decreasing.

As here thou conceivest from the triangular base aei, unto the toppe o, the triangles aoe, aoi, and eoi, to be reared up.

In the pyramis aeiou, thou seest from the quadrangular base aeio, unto the toppe u, foure triangles in like manner to be raised.

Therefore

12 The sides of a pyramis are one more than are the base.

The sides are here named Hedræ.

And

13 A pyramis is the first figure of solids.

For a pyramis in solids, is as a triangle is in plaines. For a pyramis may be resolved into other solid figures, but it cannot be resolved into any one more simple than it selfe, and which consists of fewer sides than it doth.

Therefore

14 Pyramides of equall heighth, are as their bases are 5 e, and 6. p xij.

And

15 Those which are reciprocall in base and heighth are equall 9 p xij.

These consectaries are drawne out of the 16, 18 e. iiij.

16 A tetraedrum is an ordinate pyramis comprehended of foure triangles 26. d xj.

As here thou seest. In rectilineall plaines we have in the former signified, in every kinde there is but one ordinate figure: Amongst the triangles the equilater: Amongst the quadrangles, the Quadrate: so now of all kinde of Pyramides, there is one kinde ordinate onely, and that is the Tetraedrum. And yet not every Tetraedrum is such, but that only which is comprehended of triangles, not onely severally ordinate, but equall one to another altogether alike.

Therefore

17 The edges of a tetraedrum are sixe, the plaine angles twelve, the solide angles foure.

For a Tetraedrum is comprehended of foure triangles, each of them having three sides, and three corners a peece: And every side is twise taken: Therefore the number of edges is but halfe so many.

And

18 Twelve tetraedra's doe fill up a solid place.

Because 8. solid right angles filling a place, and 12. angles of the tetraedrum are equall betweene themselves, seeing that both of them are comprehended of 24 plaine right-angles. For a solid right angle is comprehended of three plaine right angles: And therefore 8. are comprehended of 24. In like manner the angle of a Tetraedrum is comprehended of three plaine equilaters, that is of sixe third of one right angle: and therefore of two right angles: Therefore 12 are comprehended of 24.

And

19. If foure ordinate and equall triangles be joyned together in solid angles, they shall comprehend a tetraedrum.

This fabricke or construction is very easie, as you may see in these examples: For if thou shalt joyne or fold together these triangles here thus expressed, thou shalt make a tetraedrum.

20. If a right line whose power is sesquialter unto the side of an equilater triangle, be cut after a double reason, the double segment perpendicular to the center of the triangle, knit together with the angles thereof shall comprehend a tetraedrum. 13 p xiij.

For a solid to be comprehended of right lines understand plaines comprehended of right lines, as in other places following.

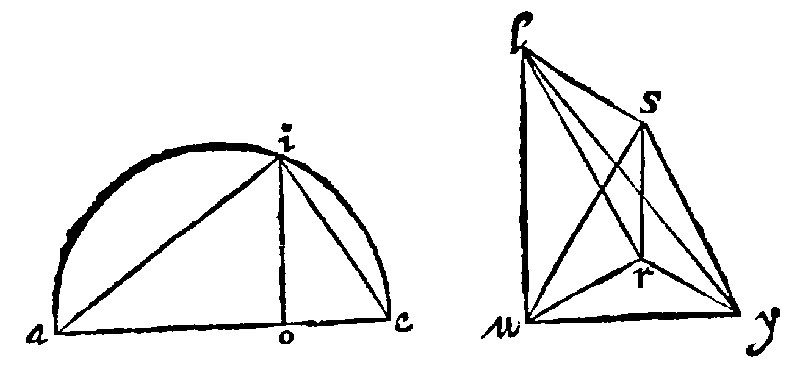
As here, Let first ae be the right line whose power is sesquialter unto ai the side of the equilater triangle, as in the forme was manifest at the 13 e xij. And let it be by the 29 e v, be cut in a double reason in o: And let the double segment ao, be perpendicular to the equilater triangle uys, unto the center r, by the 7 e xxj. And let lr be knit with the angles, by lu, ls, ly. I say that the triangles uys, usl, uyl, are equilater and equall, because all the sides are equall. First the three lower ones are equall by the grant: And the three higher ones are equall by the 9 e xij. And every one of the higher ones are equall to the under one. For if a Circle bee supposed to bee circumscribed about the triangle, the side shall be of treble power to the ray ur, by the 12 e xviij. But the higher one also is of treble power to the same ray, as is manifest in the first figure of the ray oi, which is for the ray of the second figure ur. For as ao, is to oi, so by the 9 e viij, is oi, unto oe: And by the 25 e iiij, as the first rect line ao, is unto the third oe: so is the quadrate ao, unto the quadrate oi. And by compounding ao with oe; As ae is to oe; so are the quadrates ao; and oi, that is, by the 9 e xij, the quadrate ai, unto the quadrate oi, But ae is the triple of oe. Therefore the quadrate ai, is the triple of the quadrate oi. Wherefore the higher side equall to ai, is of treble power to the ray: And therefore also all the sides are equall: And therefore againe the triangles themselves are equall.

The twenty third Booke of Geometry, of a Prisma

1 A Pyramidate is a plaine solid comprehended of pyramides.

2. A pyramidate is a Prisma, or a mingled polyedrum.

3. A prisma is a pyramidate whose opposite plaines are equall, alike, and parallell, the rest parallelogramme. 13 d xj.

As here thou seest. The base of a pyramis was but one: Of a Prisma, they are two, and they opposite one against another, First equall; Then like: Next parallell. The other are parallelogramme.

Therefore

4. The flattes of a prisma are two more than are the angles in the base.

And indeed as the augmentation of a Pyramis from a quaternary is infinite: so is it of a Prisma from a quinary: As if it be from a triangular, quadrangular, or quinquangular base; you shal have a Pentraedrum, Hexaedrum, Heptaedrum, and so in infinite.

5. The plaine of the base and heighth is the solidity of a right prisma.

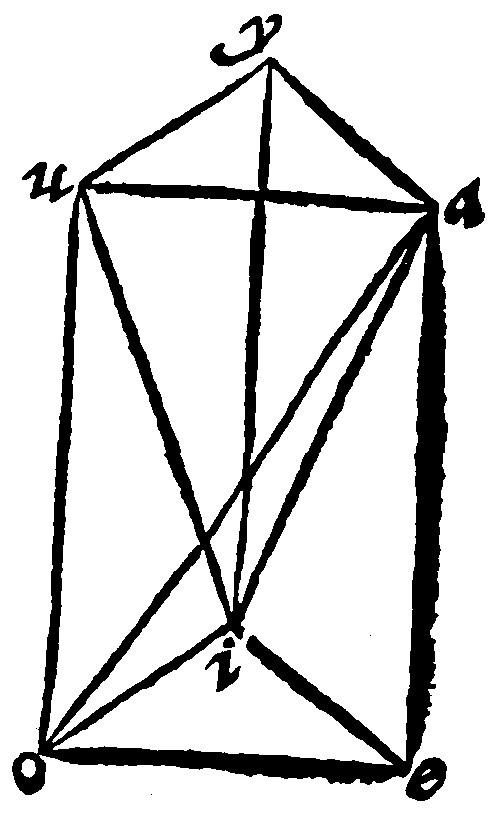
6. A prisma is the triple of a pyramis of equall base and heighth. è 7 p. xij.

As in the example a prisma pentaedrum is cut into three equall pyramides. For the first consisting of the plaines aei, aeo, aoi, eio; is equall to the second consisting of the plaines aoi, aou, aiu, iou, by the 10 e vij. Because it is equall to it both in common base and heighth. Therefore the first and second are equall. And the same second is equall to it selfe, seeing the base is iou, and the toppe a. Then also it is equall to the third consisting of the plaines aiu, aiy, uiy, auy. Therefore three are equall.

If the base be triangular, the Prisma may be resolved into prisma's of triangular bases, and the theoreme shall be concluded as afore.

Therefore

7. The plaine made of the base and the third part of the heighth is the solidity of a pyramis of equall base and heighth.

The heighth of a pyramis shall be found, if you shall take the square of the ray of the base out of the quadrate of the side: for the side of the remainder, by the 9 e xij, shall be the altitude or heighth, as in the example following.

Here the content of the triangle by the 18 e xij, is found to be 62.44/125 for the base of the pyramis. The altitude is 9.15/19: Because by the 12 e xviij, the side is of treble power to the ray. But if from 144, the quadrate of 12 the side, you take the subtriple i. 48, the remainder 96, by the 9 e xij, shall be the square of the heighth. And the side of the quadrate shall be 9.15/19. Now the third part of 9.15/19 is 3.5/19. And the plaine of 62.44/125 and 3.5/19, shall be 203.1103/2375 for the solidity of the pyramis.