The Way To Geometry

And from hence the fabricke or construction of an ordinate quinquangle upon a right line given, is manifest.

Therefore

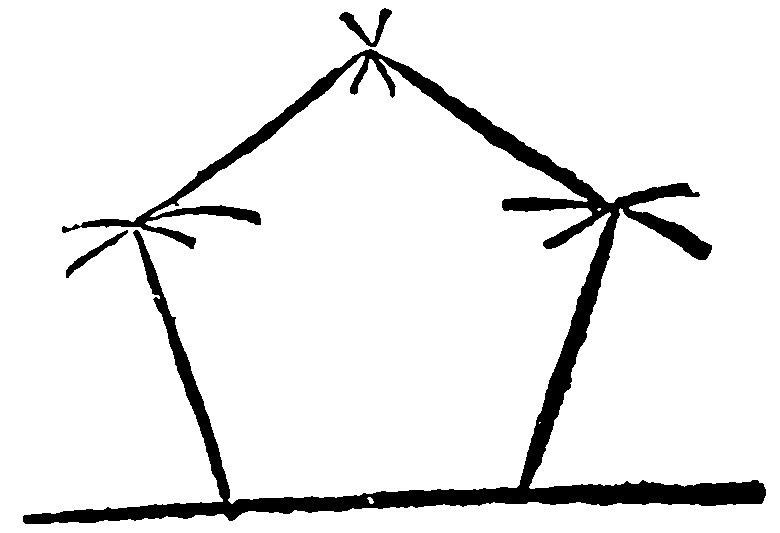
7 If a right line given, cut proportionall, be continued at each end with the greater segment, and sixe peripheries at the distance of the line given shall meete, two on each side from the ends of the line given and the continued, two others from their meetings, right lines drawne from their meetings, & the ends of the assigned shall make an ordinate quinquangle upon the assigned.

The example is thus.

8 If the diameter of a circle circumscribed about a quinquangle be rationall, it is irrationall unto the side of the inscribed quinquangle, è 11. p xiij.

So before the segments of a right line proportionally cut were irrationall.

The other triangulates hereafter multiplied from the ternary, quaternary, or quinary of the sides, may be inscribed into a circle by an inscript triangle, quadrate, or quinquangle. Therefore by a triangle there may be inscribed a triangulate of 6. 12, 24, 48, angles: By a quadrate, a triangulate of 8. 16, 32, 64, angles. By a quinquangle, a triangulate of 10, 20, 40, 80. angles, &c.

9 The ray of a circle is the side of the inscript sexangle. è 15 p iiij.

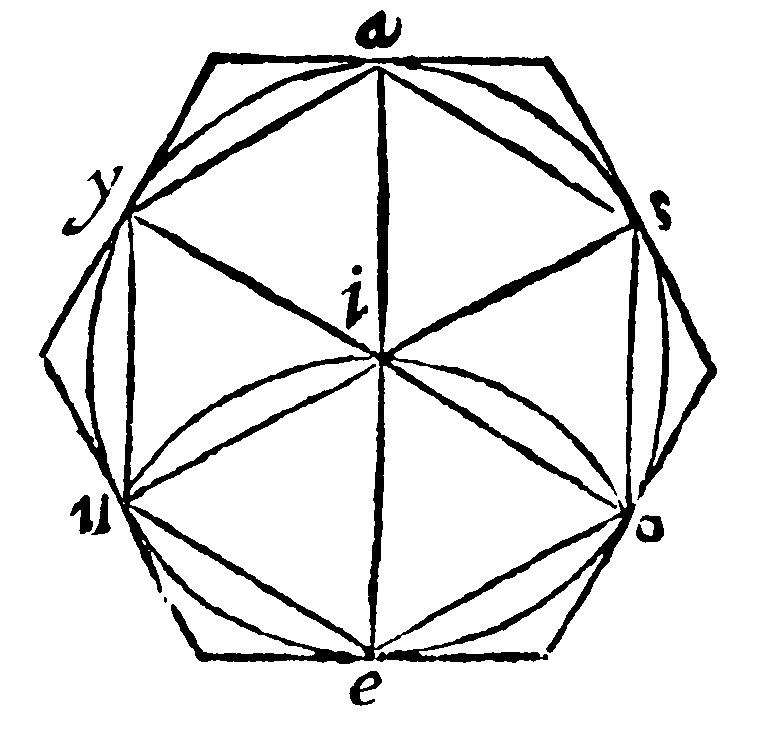
A sexangle is inscribed by an inscript equilaterall triangle, by halfing of the three angles of the said triangle: But it is done more speedily by the ray or semidiameter of the circle, sixe times continually inscribed. As in the circle given, let the diameter be ae; And upon the center o, with the ray ie, let the periphery uio, be described: And from the points o and u, let the diameters be oy, and us; These knit both one with another, and also with the diameter ae shall inscribe an equilaterall sexangle into the circle given, whose side shal be equal to the ray of the same circle. As eu, is equal to ui, because they both equall to the same ie, by the 29 e, iiij. There fore eiu, is an equilater triangle: And likewise eio, is an equilater. The angles also in the center are ⅔ of one rightangle: And therefore they are equall. And by the 14. e v, the angle sio, is ⅓. of two rightangles: And by the 15. e v. the angles at the toppe are also equall. Wherefore sixe are equall: And therefore, by the 7 e xvj. and 32. e, xv, all the bases are equall, both betweene themselves, and as was even now made manifest, to the ray of the circle given. Therefore the sexangle inscript by the ray of a circle is an equilater; And by the 1 e xvij. equiangled.

Therefore

10 Three ordinate sexangles doe fill up a place.

As here. For they are sixe equilater triangles, if you shal resolve the sexangles into sixe triangls: Or els because the angle of an ordinate sexangle is as much as one right angle and ⅓. of a right angle.

Furthermore also no one figure amongst the plaines doth fill up a place. A Quinquangle doth not: For three angles a quinquangle may make only 3.3/5 angles which is too little. And foure would make 4.4/5 which is as much too great. The angles of a septangle would make onely two rightangles, and 6/7 of one: Three would make 3, and 9/7, that is in the whole 4.2/7, which is too much, &c. to him that by induction shall thus make triall, it will appeare, That a plaine place may be filled up by three sorts of ordinate plaines onely.

And

11 If right lines from one angle of an inscript sexangle unto the third angle on each side be knit together, they shall inscribe an equilater triangle into the circle given.

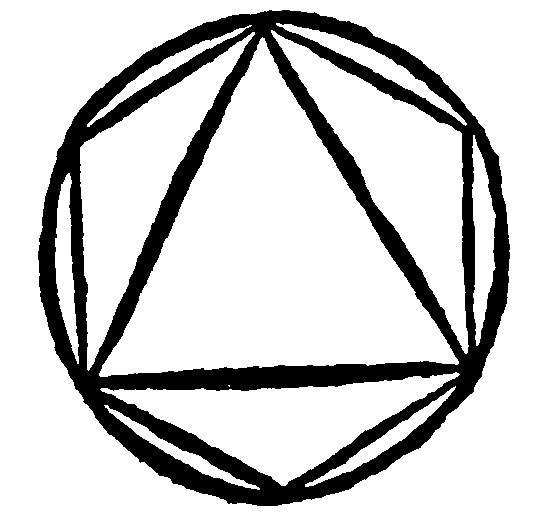
As here; Because the sides shall be subtended to equall peripheries: Therefore by the 32 e xv. they shall be equall betweene themselves: And againe, on the contrary, by such a like triangle, by halfing the angles, a sexangle is inscribed.

12 The side of an inscribed equilater triangle hath a treble power, unto the ray of the circle 12. p xiij.

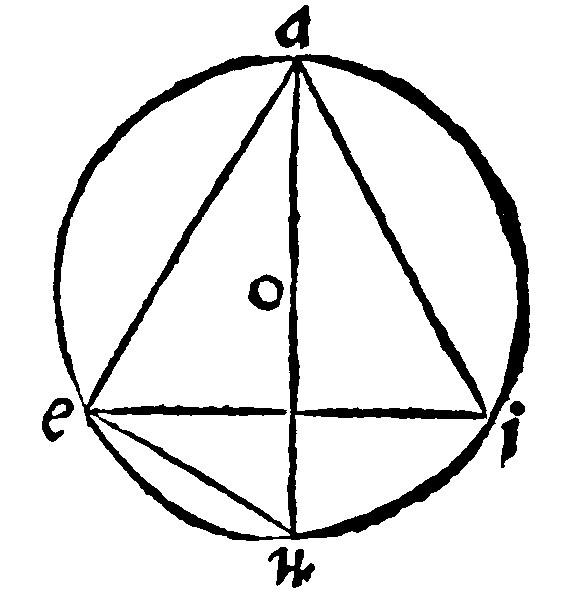
As here, with ae, one side of the triangle aei, two third parts of the halfe periphery are imployed: For with one side one third of the whole eu, is imployed: Therefore eu, is the other third part, that is, the sixth part of the whole periphery. Therefore the inscript eu, is the ray of the circle, by the 9 e. Now the power of the diameter aou, by the 14 e xij. is foure times so much as is the power of the ray, that is, of eu: And by 21. e xvj, and 9 e xij, ae, and eu, are of the same power; take away eu, and the side ae, shall be of treble power unto the ray.

13 If the side of a sexangle be cut proportionally, the greater segment shall be the side of the decangle.

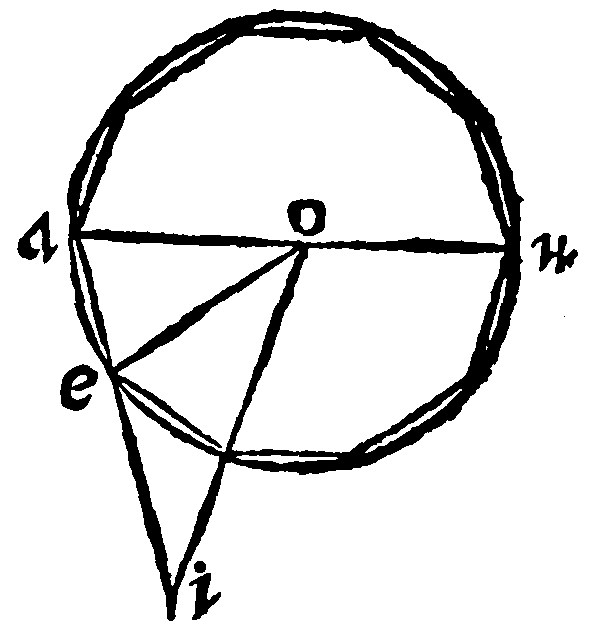
Pappus lib. 5. ca. 24. & Campanus ad 3 p xiiij. Let the ray ao, or side of the sexangle be cut proportionally, by the 3 e xiiij: And let ae, be equall to the greater segment. I say that ae, is the side of the decangle. For if it be moreover continued with the whole ray unto i, the whole aei, shall by the 4 e xiiij. be cut proportionally: and the greater segment ei, shal be the same ray. For the if the right line iea, be cut proportionally, it shall be as ia, is unto ie, that is to oa, to wit, unto the ray: so ao, shal be unto ae. Therefore, by the 15. e vij. the triangles iao, and oae, are equiangles: And the angle aoe, is equall to the angle oia. But the angle uoe, is foure times as great as the angle aoe: for it is equall to the two inner at a, and e, by the 15 e vj: which are equall between themselves, by the 10 e v. and by the 17 e vj. And therefore it is the double of aeo, which is the double, for the same cause, of aio, equall to the same aoe. Therefore uoe, is the quadruple of the said aoe. Therefore ue, is the quadruple of the periphery ea. Therefore the whole uea, is the quintuple of the same ea: And the whole periphery is decuple unto it. And the subtense ae, is the side of the decangle.

Therefore

14 If a decangle and a sexangle be inscribed in the same circle, a right line continued and made of both sides, shall be cut proportionally, and the greater segment shall be the side of a sexangle; and if the greater segment of a right line cut proportionally be the side of an hexagon, the rest shall be the side of a decagon. 9. p xiij.

The comparison of the decangle and the sexangle with the quinangle followeth.

15 If a decangle, a sexangle, and a pentangle be inscribed into the same circle the side of the pentangle shall in power countervaile the sides of the others. And if a right line inscribed do countervaile the sides of the sexangle and decangle, it is the side of the pentangle. 10. p xiiij.

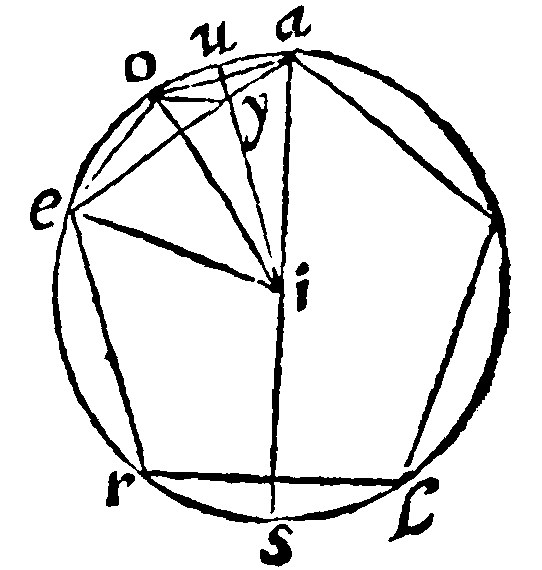
Let the side of the inscribed quinquangle be ae: of the sexangle, ei: Of the decangle ao. I say, the side ae, doth in power countervaile the rest. For let there be two perpēdiculars: The first io, the second iu, cutting the sides of the quinquangle and decangle into halves: And the meeting of the second perpendicular with the side of the quinquangle let it be y. The syllogisme of the demonstration is this: The oblongs of the side of the quinquangle, and the segments of the same, are equall to the quadrates of the other sides. But the quadrate of the same whole side, is equall to the oblongs of the whole, and the segments, by the 3 e, xiij. Therefore it is equall to the quadrates of the other sides.

Let the proportion of this syllogisme be demonstrated: For this part onely remaineth doubtfull. Therefore two triangles, aei, and yei, are equiangles, having one common angle at e: And also two equall ones aei, and eiy, the halfes, to wit, of the same eis: Because that is, by the 17 e, vj: one of the two equalls, unto the which eis, the out angle, is equall, by the 15 e. vj. And this doth insist upon a halfe periphery. For the halfe periphery als, is equall to the halfe periphery ars: and also al, is equall to ar. Therefore the remnant ls, is equall to the remnant rs: And the whole rl, is the double of the same rs: And therefore er, is the double of eo: And rs, the double of ou. For the bisegments are manifest by the 10 e, xv. and the 11 e, xvj. Therefore the periphery ers, is the double of the periphery eou: And therefore the angle eiu, is the halfe of the angle eis, by the 7 e, xvj. Therefore two angles of two triangles are equall: Wherefore the remainder, by the 4 e vij, is equall to the remainder. Wherefore by the 12 e, vij, as the side ae, is to ei: so is ei, to ey. Therefore by the 8 e xij, the oblong of the extreames is equall to the quadrate of the meane.

Now let oy, be knit together with a straight: Here againe the two triangles aoe, and aoy, are equiangles, having one common angle at a: And aoy, and oea, therefore also equall: Because both are equall to the angle at a: That by the 17 e, vj: This by the 2 e, vij: Because the perpendicular halfing the side of the decangle, doth make two triangles, equicrurall, and equall by the right angle of their shankes: And therefore they are equiangles. Therefore as ea, is to ao: so is ea, to ay. Wherefore by the 8 e, xij. the oblong of the two extremes is equall to the quadrate of the meane: And the proposition of the syllogisme, which was to be demonstrated. The converse from hence as manifest Euclide doth use at the 16 p xiij.

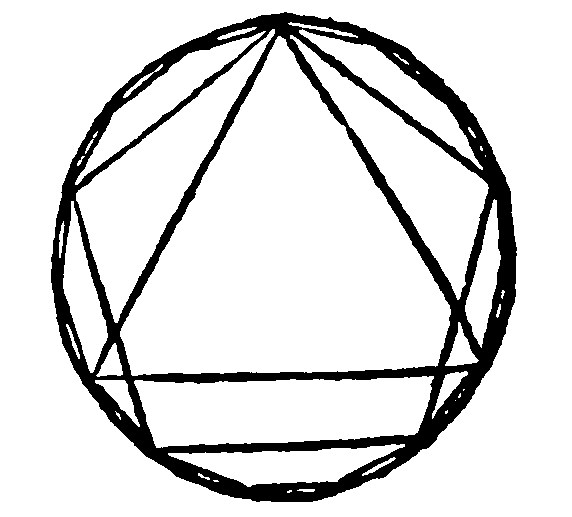
16. If a triangle and a quinquangle be inscribed into the same Circle at the same point, the right line inscribed betweene the bases of the both opposite to the said point, shall be the side of the inscribed quindecangle. 16. p. iiij.

For the side of the equilaterall triangle doth subtend 1/3 of the whole pheriphery. And two sides of the ordinate quinquangle doe subtend 2/5 of the same. Now 2/5 – 1/3 is 1/15: Therefore the space betweene the triangle, and the quinquangle shall be the 1/15 of the whole periphery.

Therefore

17. If a quinquangle and a sexangle be inscribed into the same circle at the same point, the periphery intercepted beweene both their sides, shall be the thirtieth part of the whole periphery.

As here. Therefore the inscription of ordinate triangulates, of a Quadrate, Quinquangle, Sexangle, Decangle, Quindecangle is easie to bee performed by one side given or found, which reiterated as oft as need shall require, shal subtend the whole periphery. Jun. 4. A. C.

Campana pulsante pro. H. W.

Of Geometry the ninteenth Booke; Of the Measuring of ordinate Multangle and of a Circle

Out of the Adscription of a Circle and a Rectilineall is drawne the Geodesy of ordinate Multangles, and first of the Circle it selfe. For the meeting of two right lines equally, dividing two angles is the center of the circumscribed Circle: From the center unto the angle is the ray: And then if the quadrate of halfe the side be taken out of the quadrate of the ray, the side of the remainder shall be the perpendicular, by the 9 e xij. Therefore a speciall theoreme is here thus made:

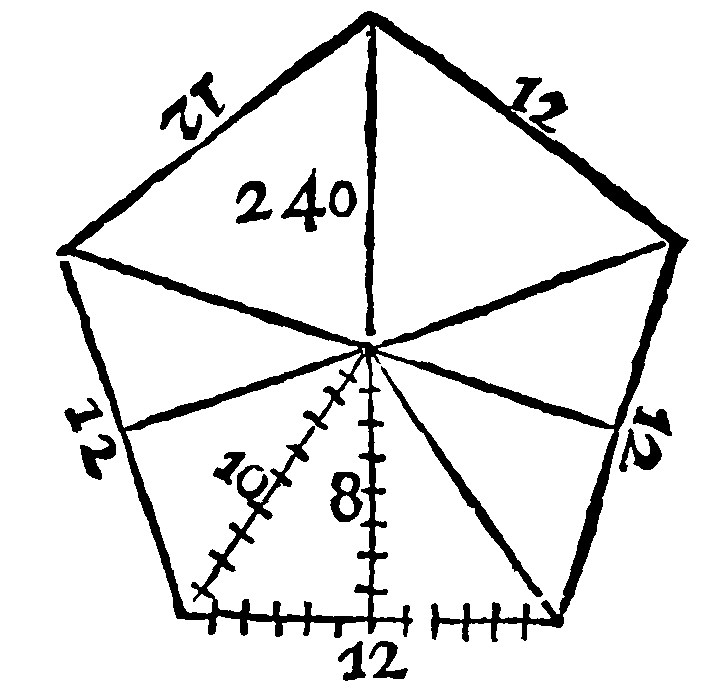
1. A plaine made of the perpendicular from the center unto the side, and of halfe the perimeter, is the content of an ordinate multangle.

As here; The quadrate of 10, the ray is 100. The quadrate of 6, the halfe of the side 12, is 36: And 100. 36 is 64, the quadrate of the Perpendicular, whose side 8, is the Perpendicular it selfe. Now the whole periphery of the Quinquangle, is 60. The halfe thereof therefore is 30. And the product of 30, by 8, is 240, for the content of the sayd quinquangle.

The Demonstration here also is of the certaine antecedent cause thereof. For of five triangles in a quinquangle, the plaine of the perpendicular, and of halfe the base is one of them, as in the former hath beene taught: Therefore five such doe make the whole quinquangle. But that multiplication, is a multiplication of the Perpendicular by the Perimeter or bout-line.

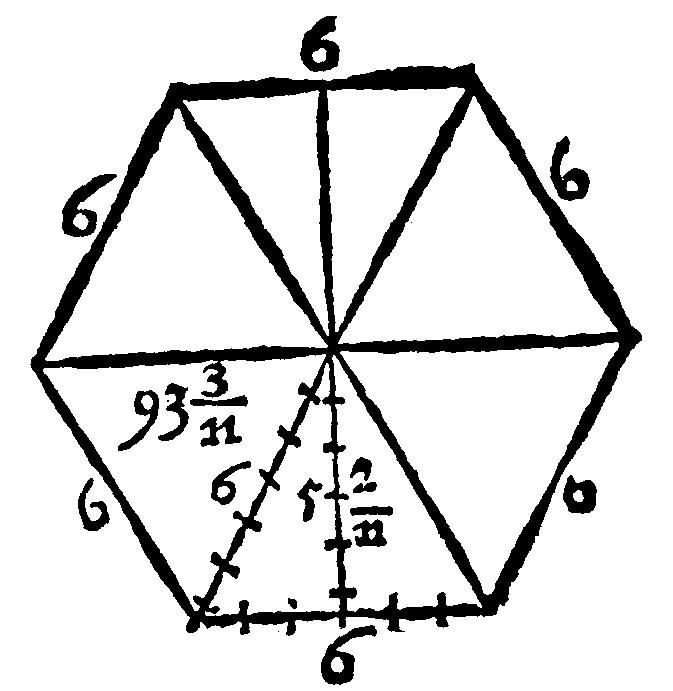
In an ordinate Sexangle also the ray, by the 9 e xviij, is knowne by the side of the sexangle. As here, the quadrate of 6, the ray is 36. The quadrate of 3, the halfe of the side, is 9: And 36 – 9. are 27, for the quadrate of the Perpendicular, whose side 5.2/11 is the perpendicular it selfe. Now the whole perimeter, as you see, is 36. Therefore the halfe is 18. And the product of 18 by 5.2/11 is 93.3/11 for the content of the sexangle given.

Lastly in all ordinate Multangles this theoreme shall satisfie thee.

2 The periphery is the triple of the diameter and almost one seaventh part of it.

Or the Periphery conteineth the diameter three times and almost one seventh of the same diameter. That it is triple of it, sixe raies, (that is three diameters) about which the periphery, the 9 e xviij, is circumscribed doth plainely shew: And therefore the continent is the greater: But the excesse is not altogether so much as one seventh part. For there doth want an unity of one seventh: And yet is the same excesse farre greater than one eighth part. Therefore because the difference was neerer to one seventh, than it was to one eighth, therefore one seventh was taken, as neerest unto the truth, for the truth it selfe.

Therefore

3. The plaine of the ray, and of halfe the periphery is the content of the circle.

For here 7, the ray, of halfe the diameter 14, Multiplying 22, the halfe of the periphery 44, maketh the oblong 154, for the content of the circle. In the diameter two opposite sides, and likewise in the perimeter the two other opposite sides of the rectangle are conteined. Therefore the halfes of those two are taken, of the which the rectangle is comprehended.

And

4. As 14 is unto 11, so is the quadrate of the diameter unto the Circle.

For here 3 bounds of the proportion are given in potentia: The fourth is found by the multiplication of the third by the second, and by the Division of the product by the first: As here the Quadrate of the diameter 14, is 196. The product of 196 by 11 is 2156. Lastly 2156 divided by 14, the first bound, giveth in the Quotient 154, for the content of the circle sought. This ariseth by an analysis out of the quadrate and Circle measured. For the reason of 196, unto a 154; is the reason of 14 unto 11, as will appeare by the reduction of the bounds.

This is the second manner of squaring of a circle taught by Euclide as Hero telleth us, but otherwise layd downe, namely after this manner. If from the quadrate of the diameter you shall take away 3/14 parts of the same, the remainder shall be the content of the Circle. As if 196, the quadrate be divided by 14, the quotient likewise shall be 14. Now thrise 14, are 42: And 196 – 42, are 154, the quadrate equall to the circle.

Out of that same reason or rate of the pheriphery and diameter ariseth the manner of measuring of the Parts of a circle, as of a Semicircle, a Sector, a Section, both greater and lesser.

And

5. The plaine of the ray and one quarter of the periphery, is the content of the semicircle.

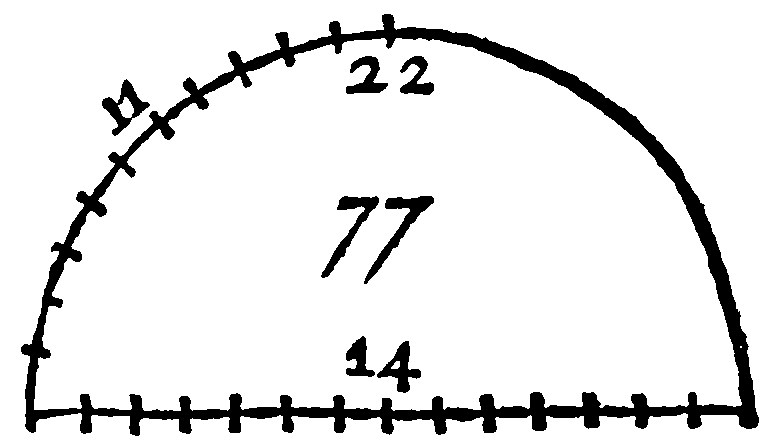
As here thou seest: For the product of 7, the halfe of the diameter, multiplyed by 11, the quarter of the periphery, doth make 77, for the content of the semicircle.

This may also be done by taking of the halfe of the circle now measured.

And

6. The plaine made of the ray and halfe the base, is the content of the Sector.

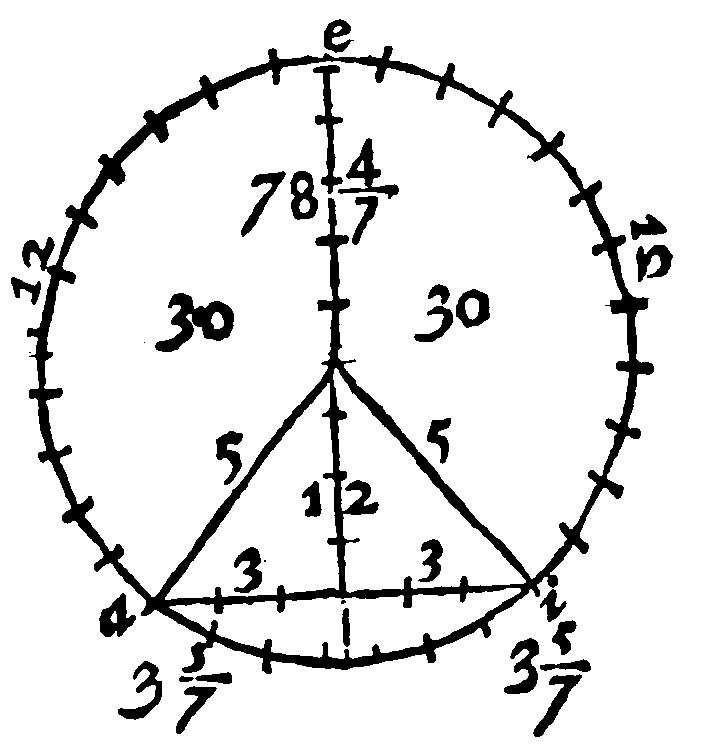
Here are three sectours, ae the base of 12 foote: And ei in like manner of 12 foote. The other or remainder ia of 7 f. and 3/7 of one foote. The diameter is 10 foote. Multiply therefore 5, halfe of the diameter, by 6 halfe of the base, and the product 30, shall be the content of the first sector. The same shall also be for the second sectour. Againe multiply the same ray or semidiameters 5, by 3.5/7, the halfe of 7.3/7, the product of 18.4/7 shall be the content of the third sector. Lastly, 30 + 30 + 18.4/7 are 78.4/7, the content of the whole circle.

And

7. If a triangle, made of two raies and the base of the greater section, be added unto the two sectors in it, the whole shall be the content of the greater section: If the same be taken from his owne sector, the remainder shall be the content of the lesser.

In the former figure the greater section is aei: The lesser is ai. The base of them both is as you see, 6. The perpendicular from the toppe of the triangle, or his heighth is 4. Therefore the content of the triangle is 12. Wherefore 30 + 30 + 12, that is 72, is the content of the greater section aei. And the lesser sectour, as in the former was taught, is 18.4/7. Therefore 18.4/7 – 12, that is, 6.4/7, is the content of ai, the lesser section.

And

8. A circle of unequall isoperimetrall plaines is the greatest.

The reason is because it is the most ordinate, and comprehended of most bounds; see the 7, and 15 e iiij. As the Circle a, of 24 perimeter, is greater then any rectilineall figure, of equall perimeter to it, as the Quadrate e, or the Triangle i.

Of Geometry the twentieth Booke, Of a Bossed surface

1. A bossed surface is a surface which lyeth unequally betweene his bounds.

It is contrary unto a Plaine surface, as wee heard at the 4 e v.

2. A bossed surface is either a sphericall, or varium.

3. A sphericall surface is a bossed surface equally distant from the center of the space inclosed.

Therefore

4. It is made by the turning about of an halfe circumference the diameter standeth still. è 14 d xj.

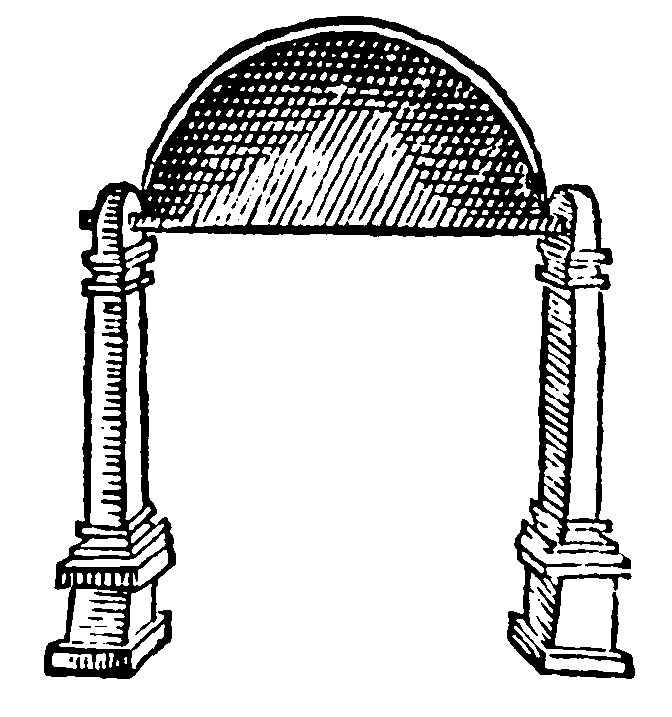
As here if thou shalt conceive the space betweene the periphery and the diameter to be empty.

5. The greatest periphery in a sphericall surface is that which cutteth it into two equall parts.

Those things which were before spoken of a circle, the same almost are hither to bee referred. The greatest periphery of a sphericall doth answere unto the Diameter of a Circle.

Therefore

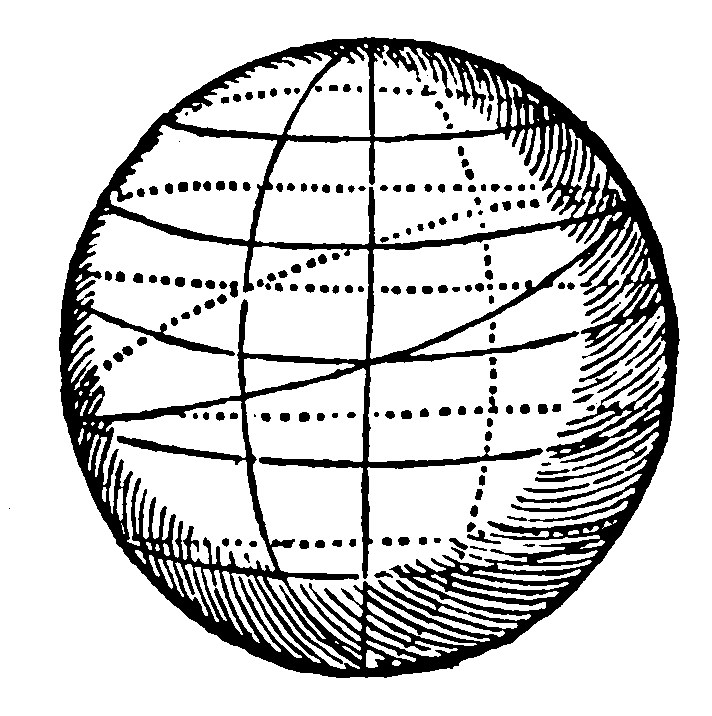
6. That periphery that is neerer to the greatest, is greater than that which is farther off: And on each side those two which are equally distant from the greatest, are equall.

The very like unto those which are taught at the 15, 16, 17, 18. e. xv. may here againe be repeated: As here.

7 The plaine made of the greatest periphery and his diameter is the sphericall.

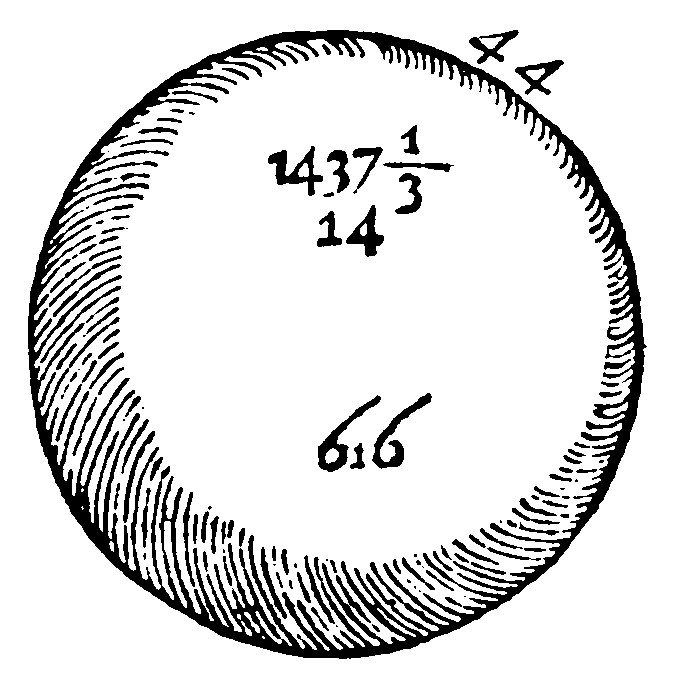
So the plaine made of the diameter 14. and of 44. the greatest periphery, which is 616. is the sphericall surface. So before the content of a circle was measured by a rectangle both of the halfe diameter, and periphery. But here, by the whole periphery and whole diameter, there is made a rectangle for the measure of the sphericall, foure times so great as was that other: Because by the 1 e vj. like plaines (such as here are conceived to be made of both halfe the diameter, and halfe the periphery, and both of the whole diameter and whole periphery) are in a doubled reason of their homologall sides.

Therefore

8 A plaine of the greatest circle and 4, is the sphericall.

This consectarium is manifest out of the former element.

And

9 As 7 is to 22. so is the quadrate of the diameter unto the sphericall.

For 7, and 22, are the two least bounds in the reason of the diameter unto the periphery: But in a circle, as 14, is to 11, so is the quadrate of the diameter unto the circle. The analogie doth answer fitly: Because here thou multipliest by the double, and dividest by the halfe: There contrariwise thou multipliest by the halfe, and dividest by the double. Therefore there one single circle is made, here the quadruple of that. This is, therefore the analogy of a circle and sphericall; from whence ariseth the hemispherical, the greater and the lesser section.

And

10 The plaine of the greatest periphery and the ray, is the hemisphericall.

As here, the greatest periphery is 44. the ray 7. The product therefore of 44. by 7. that is, 308. is the hemisphericall.

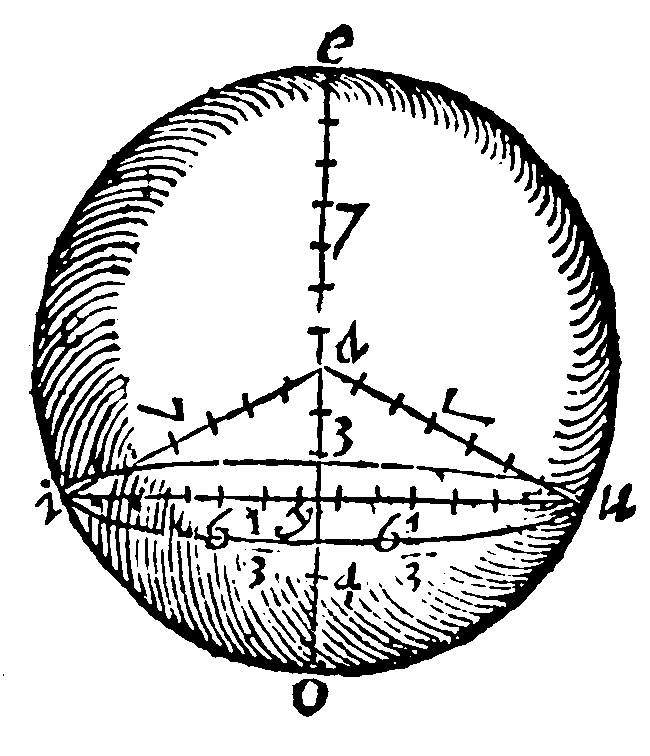
11 If looke what the part be of the ray perpendicular from the center unto the base of the greater section, so much the hemisphericall be increased, the whole shall be the greater section of the sphericall: But if it be so much decreased, the remainder shall be the lesser.

As in the example, the part of the third ray, that is, of 3/7, is from the center: such like part of the hemispherical 308, is 132. (For the 7, part of 308. is 44. And three times 44. is 132.) Therefore 132. added to 308. do make 440. for the greater section of the sphericall. And 132. taken from 308. doe leave 176. for the lesser section of the same.

12 The varium is a bossed surface, whose base is a periphery, the side a right line from the bound of the toppe, unto the bound of the base.

13 A varium is a conicall or a cylinderlike forme.

14 A conicall surface is that which from the periphery beneath doth equally waxe lesse and lesse unto the very toppe.

Therefore

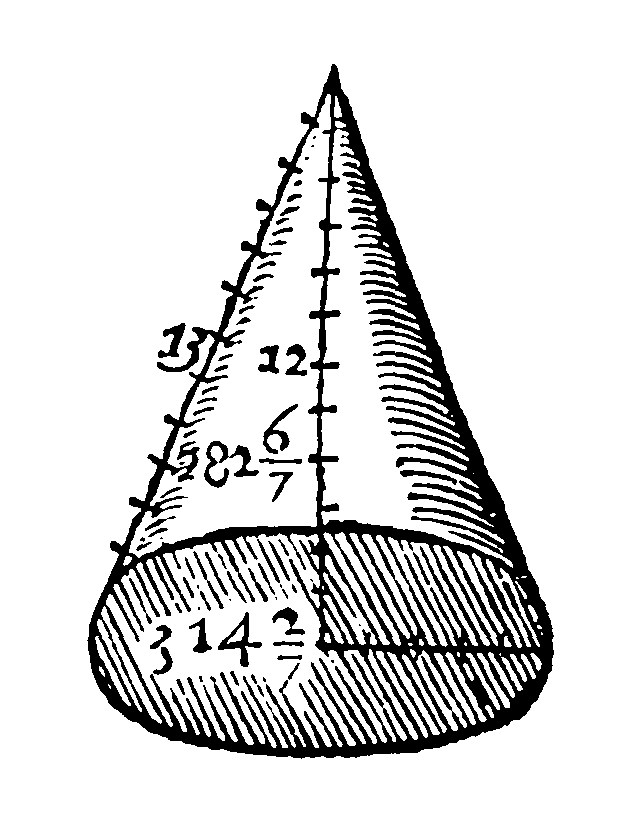
15. It is made by turning about of the side about the periphery beneath.

16 The plaine of the side and halfe the base is the conicall surface.

As in the example next aforegoing, the side is 13. The halfe periphery is 15.5/7: And the product of 15.5/7 by 13. is 204.2/7. for the conicall surface. To which if you shall adde the circle underneath, you shall have the whole surface.