The Way To Geometry

So also looke how much the straightening or pressing together is greater, so much is the inequality of the obtuse and acute angles the greater. As here.

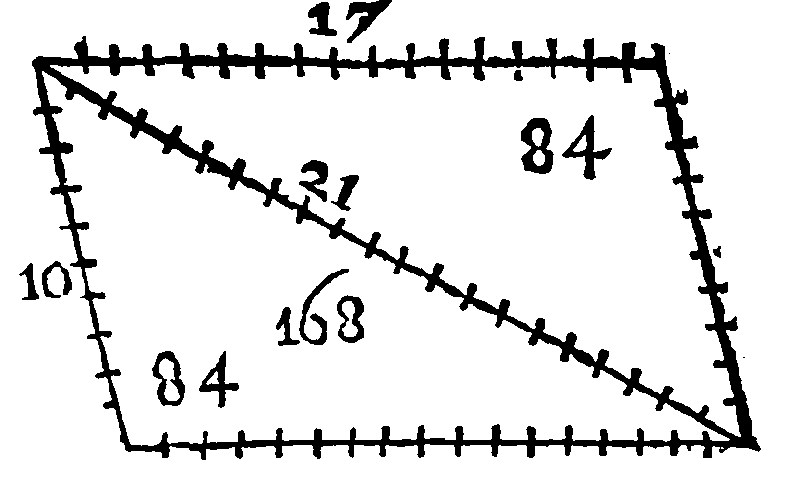
And the Rhomboides is so called as one would say Rhombuslike, although beside the inequality of the angles it hath nothing like to a Rhombus. An example of measuring of a Rhomboides is thus.

11 A Trapezium is a quadrangle not parallelogramme. 34. d j.

Of the quadrangles the Trapezium remaineth for the last place: Euclide intreateth this fabricke to be granted him, that a Trapezium may be called as it were a little table: And surely Geometry can yeeld no reason of that name.

The examples both of the figure and of the measure of the same let these be.

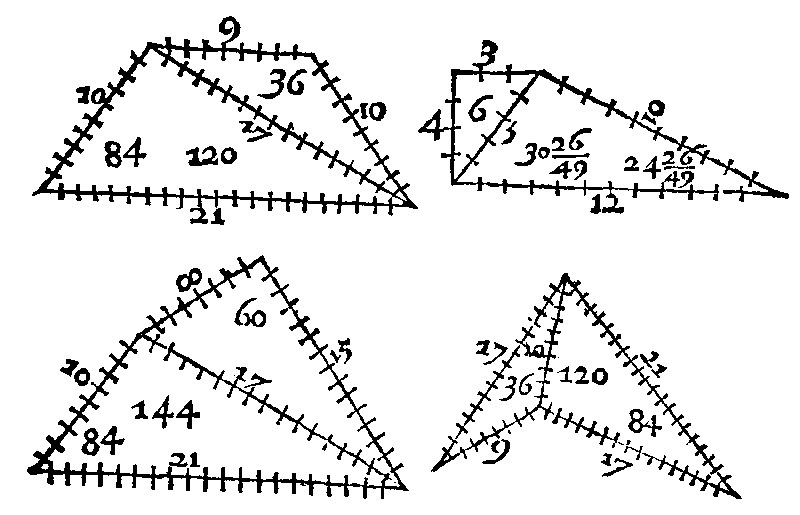
Therefore triangulate quadrangles are of this sort.

12 A multangle is a figure that is comprehended of more than foure right lines. 23. d j.

By this generall name, all other sorts of right lined figures hereafter following, are by Euclide comprehended, as are the quinquangle, sexangle, septangle, and such like inumerable taking their names of the number of their angles.

In every kinde of multangle, there is one ordinate, as we have in the former signified, of which in this place we will say nothing, but this one thing of the quinquangle. The rest shall be reserved untill we come to Adscription.

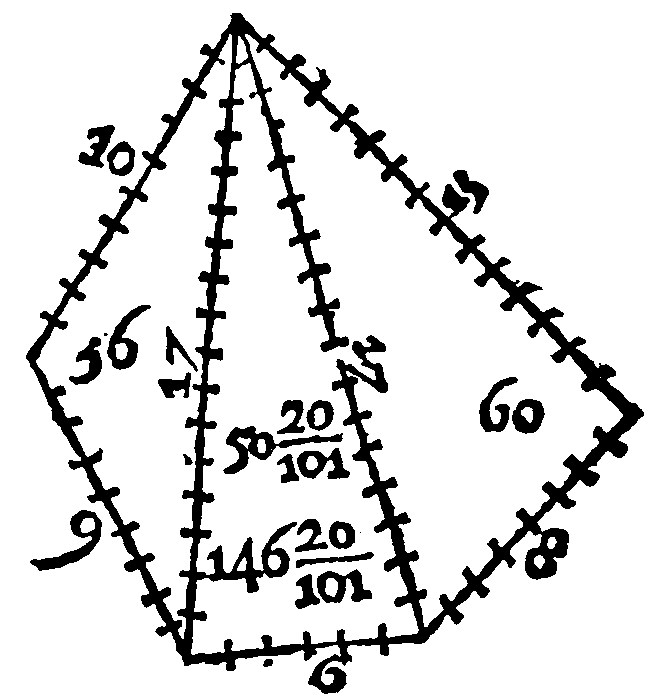
13 Multangled triangulates doe take their measure also from their triangles.

As here, this quinquangle is measured by his three triangles. The first triangle, whose sides are 9. 10. and 17. by the 18. e xij. is 36. The second, whose sides are 6, 17, and 17. by the same e, is 50.20/101. The third, whose sides are 17, 15. and 8. by the same, is 60. And the summe of 36. 50.20/101. and 60. is 146.20/101, for the whole content of the Quinquangle given.

14 If an equilater quinquangle have three sides equall, it is equiangled. 7 p 13.

This of some, from the Greeke is called Pentagon; of others a Pentangle, by a name partly Greeke partly Latine.

As in the Quinquangle aeiou, the three angles at a, e, and i, are equall: Therefore the other two are equall: And they are equall unto these. For let eu, ai, ia, be knit together with right lines. Here the triangles aei, and eau. by the grant, and by the 2 and 1 e vij. are equilaters and equiangles: And the Bases ai, and eu, are equall: And the Angles, eai, and aue, are equall: Item aeu, and eia. Therefore ay, and ye, are equall, by the 17 e vj. Item the remainder uy, is equall to the remainder yi, when from equals equals be subtracted. Moreover by the grant, and by the 17 e vj, oui, and oiu, are equall. Wherefore three are equall; And therefore the whole angle is equall at u, to the whole angle at i. And therefore it is equall to those which are equall to it.

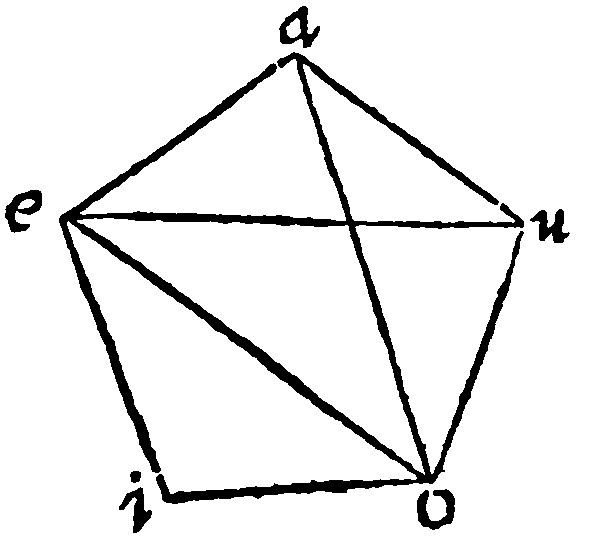
I say moreover that the angle at o, is likewise equall, if ao, and oe, be knit together with a right line, as here: For three in like manner do come to be equall.

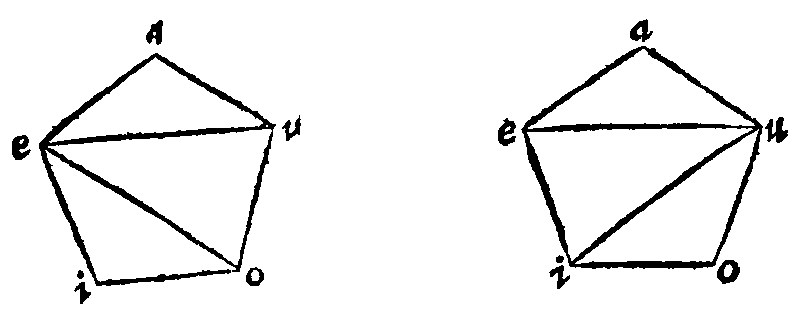
But if the three angles non deinceps not successively following be equall, as aio, the businesse will yet be more easie, as here: For the angles eua, and eoi, are equall by the grant: And the inner also eou, and euo. Therefore the wholes of two are equall. Of the other at e, the same will fall out, if iu, be knit together with a right line iu, as here: For the wholes of two shall be equall.

The fifteenth Booke of Geometry, Of the Lines in a Circle

As yet we have had the Geometry of rectilineals: The Geometry of Curvilineals, of which the Circle is the chiefe, doth follow.

1. A Circle is a round plaine. è 15 d j.

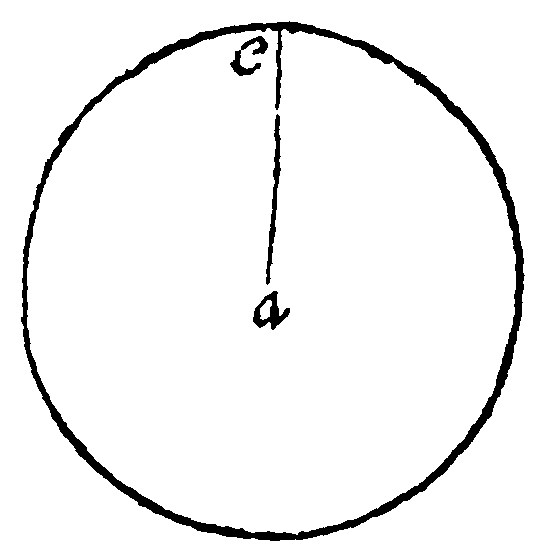
As here thou seest. A Rectilineall plaine was at the 3 e vj, defined to be a plaine comprehended of right lines. And so also might a circle have beene defined to be a plaine comprehended of a periphery or bought-line, but this is better.

The meanes to describe a Circle, is the same, which was to make a Periphery: But with some difference: For there was considered no more but the motion, the point in the end of the ray describing the periphery: Here is considered the motion of the whole ray, making the whole plot conteined within the periphery.

A Circle of all plaines is the most ordinate figure, as was before taught at the 10 e iiij.

2 Circles are as the quadrates or squares made of their diameters 2 p. xij.

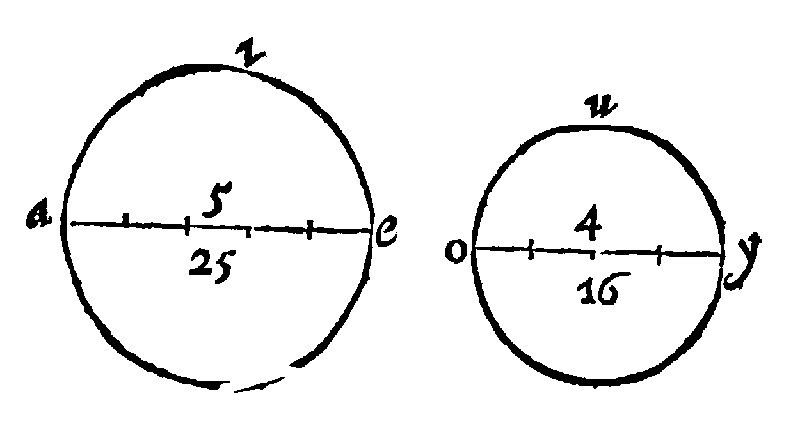
For Circles are like plaines. And their homologall sides are their diameters, as was foretold at the 24 e iiij. And therefore by the 1 e vj, they are one to another, as the quadrates of their diameters are one to another, which indeed is the double reason of their homologall sides. As here the Circle aei, is unto the Circle ouy as 25, is unto 16, which are the quadrates of their Dieameters, 5 and 4.

Therefore

3. The Diameters are, as their peripheries Pappus, 5 l. xj, and 26th. 18.

As here thou seest in ae, and io.

4. Circular Geometry is either in Lines, or in the segments of a Circle.

This partition of the subject matters howsoever is taken for the distinguishing and severing with some light a matter somewhat confused; And indeed concerning lines, the consideration of secants is here the foremost, and first of Inscripts.

5. If a right line be bounded by two points in the periphery, it shall fall within the Circle. 2 p iij.

As here ae, because the right within the same points is shorter, than the periphery is, by the 5 e ij.

From hence doth follow the Infinite section, of which we spake at the 6 e j.

This proposition teacheth how a Rightline is to be inscribed in a circle, to wit, by taking of two points in the periphery.

6. If from the end of the diameter, and with a ray of it equal to the right line given, a periphery be described, a right line drawne from the said end, unto the meeting of the peripheries, shall be inscribed into the circle, equall to the right line given. 1 p iiij.

As let the right line given be a: And from e, the end of the diameter ei: And with eo, a part of it equall to a, the line given, describe the circle eu: A right line eu, drawne from the end e, unto u, the meeting of the two peripheries, shall be inscribed in the circle given, by the 5 e, equall to the line given; because it is equall to eo, by the 10 e v, seeing it is a ray of the same Circle.

And this proposition teacheth, How a right line given is to be inscribed into a Circle, equall to a line given.

Moreover of all inscripts the diameter is the chiefe: For it sheweth the center, and also the reason or proportion of all other inscripts. Therefore the invention and making of the diameter of a Circle is first to be taught.

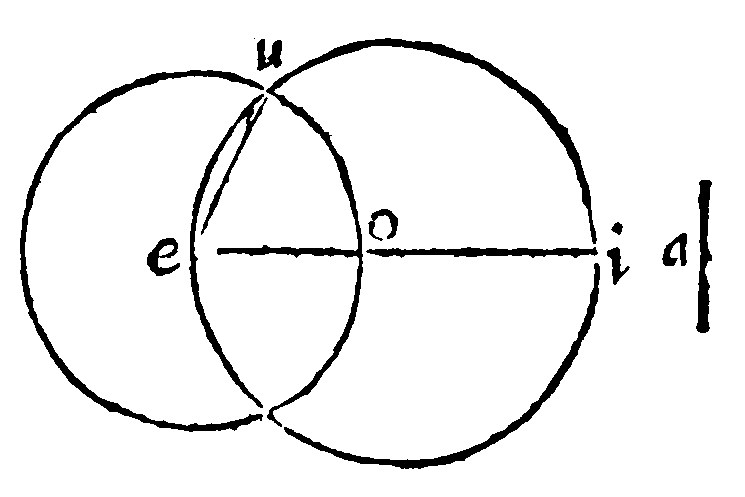
7. If an inscript do cut into two equall parts, another inscript perpendicularly, it is the diamiter of the Circle, and the middest of it is the center. 1 p iij.

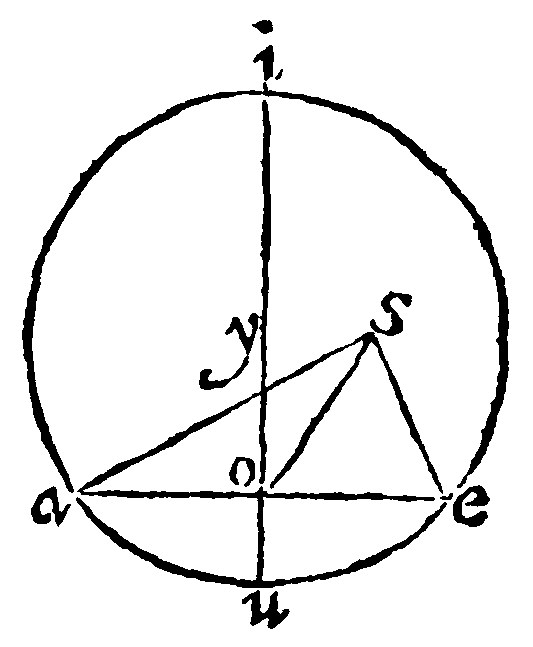
As let the Inscript ae, cut the inscript iu perpendicularly: dividing it into two equall parts in o. I say that the one inscript thus halfing the other, is the diameter of the Circle: And that the middest of it is the center thereof: As in the circle, let the Inscript is, cut the inscript ae, and that perpendicularly dividing into two equall parts in o. I say that iu, thus dividing ae, is the Diameter of the Circle: And y, the middest of the said iu, is the Center of the same.

The cause is the same, which was of the 5 e xj. Because the inscript cut into halfes is for the side of the inscribed rectangle, and it doth subtend the periphery cut also into two parts; By the which both the Inscript and Periphery also were in like manner cut into two equall parts: Therefore the right line thus halfing in the diameter of the rectangle: But that the middle of the circle is the center, is manifest out of the 7 e v, and 29 e iiij.

Euclide, thought better of Impossibile, than he did of the cause: And thus he forceth it. For if y be not the Center, but s, the part must be equall to the whole: For the Triangle aos, shall be equilater to the triangle eos. For ao, oe, are equall by the grant: Item sa, and se, are the rayes of the circle: And so, is common to both the triangles. Therefore by the 1 e vij, the angles on each side at o are equall; And by the 13 e v, they are both right angles. Therefore soe is a right angle; It is therefore equall by the grant, to the right angle yoe, that is, the part is equall to the whole, which is impossible. Wherefore s is not the Center. The same will fall out of any other points whatsoever out of y.

Therefore

8. If two right lines doe perpendicularly halfe two inscripts, the meeting of these two bisecants shall be the Center of the circle è 25 p iij.

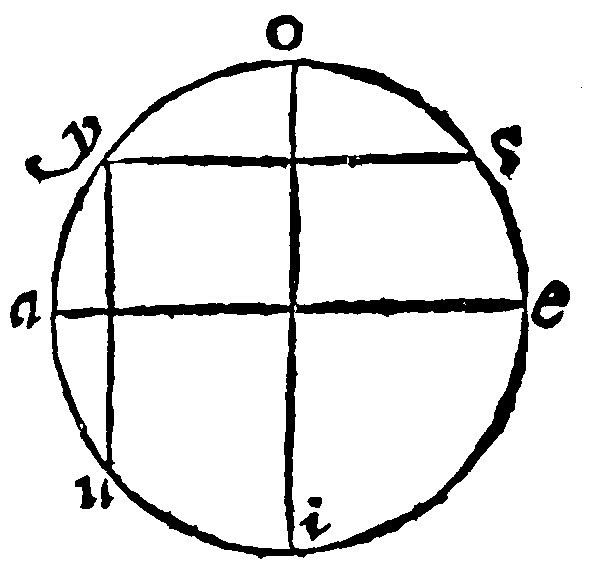
As here ae, and io, let them cut into halfes the right lines uy, and ys. And let them meete, that they cut one another in r. I say r is the center of the circle ayoseiu. For before, at the 6, and 7 e, it was manifest that the Center was in the Diameter. And in the meeting of the diameters. [Therefore two manner of wayes is the Center found; First by the middle of the diameter: And then againe by the concourse, or meeting of the diameters, in the middest of the lines halfed or cut into two equall portions.] Here is no neede of the meeting of many diameters, one will serve well enough.

And one may

9. Draw a periphery by three points, which doe not fall in a right line.

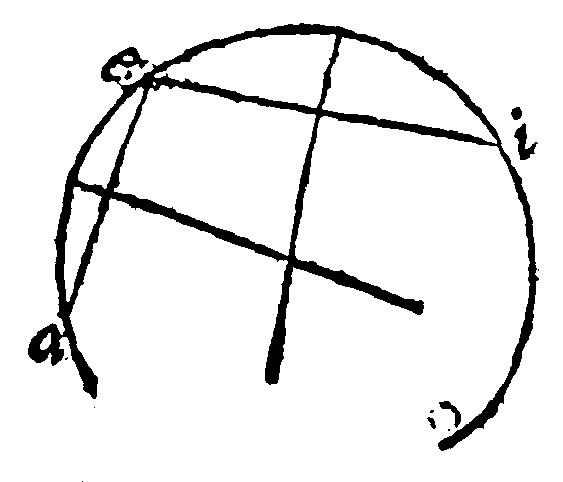
As here, by aei, (First from a, to e, let a right line be drawne; And likewise from e to i. Then, by the 12 e v, let both these lines be cut into equall parts, by two infinite right lines: These halfing lines also shall meete: And in their meeting shall be the Center, by the 8 e. And therefore from that meeting unto any of the sayd points given is the ray of the periphery desired.)

10. If a diameter doe halfe an inscript, that is, not a diameter, it doth cut it perpendicularly: And contrariwise: 3 p iij.

As let the diameter ae, halfe the inscript io, which is not a diameter: And let the raies of the circle bee ui, and uo. The cause in all is the same, which was of the 5 e xj.

11. If inscripts which are not diameters doe cut one another, the segments shall be unequall. 4 p iij.

This is a consectary drawne out of the 28 e iiij. For if the inscripts were halfed, they should be diameters, against the grant.

But rate hath beene hitherto in the parts of inscripts: Proportion in the same parts followeth.

12 If two inscripts doe cut one another, the rectangle of the segments of the one is equall to the rectangle of the segments of the other. 35 p iij.

If the inscripts thus cut be diameters, the proportion is manifest, as in the first figure. For the Rectangle of the segments, of the one is equall to the rectangle of the segments of the other, seeing they be both quadrates of equall sides. If they be not diameters let them otherwise as ae, and io: I say the Oblong of au, and ue, is equall to the Oblong of ou, and ui. For let the raies from the Center y, be ye, and yi. To the quadrate of each of these both the rectangles of the segments shall be equall. For by the 7 e, let the diameter yu, fall upon the point of the common section u; And let ys, and sr, be perpendiculars. Here by the 5 e xj. the inscripts are cut equally in the points r and s: And unequally in the point u: Therefore by the 7 e xiij, the oblong, of ou, and ui, with the quadrate su, is equall to the quadrates si; And adding ys, the same oblong, with the quadrates us and sy, that is, by the 9 e xij, with the quadrate yu, is equall to the quadrates is and sy, that is, by the 9 e xij, to the quadrate iy, that is, by the 5 e xij, to ye, to the which by the same cause it is manifest the other oblong with the quadrate yu is equall. Let the quadrate yu, bee taken from each of them: And then the oblongs shall be equall to the same: And therefore betweene themselves.

And this is the comparison of the parts inscripts. The rate of whole inscripts doth follow, the which whole one diameter doth make:

13 Inscripts are equall distant from the center, unto which the perpendiculars from the center are equall 4 d iij.

As it appeareth in the next figure, of the lines ae and io, unto which the perpendiculars uy and us, from the Center u, are equall.

14. If inscripts be equall, they be equally distant from the center: And contrariwise. 13 p iij.

The diameters in the same circle, by the 28 e iiij, are equall: And they are equally distant from the center, seeing they are by the center, or rather are no whit at all distant from it: Other inscripts are judged to be equall, greater, or lesser one than another, by the diameter, or by the diameters center.

Euclide doth demonstrate this proposition thus: Let first ae and io be equall; I say they are equidistant from the center. For let uy, and us, be perpendiculars: They shall cut the assigned ae, & io, into halfes, by the 5 e xj: And ya and si are equall, because they are the halfes of equals. Now let the raies of the circle be ua, and ui: Their quadrates by the 9 e xij, are equall to the paire of quadrates of the shankes, which paires are therefore equall betweene themselves. Take from equalls the quadrates ya, and si, there shall remaine yu, and us, equalls: and therefore the sides are equall, by the 4 e 12.

The converse likewise is manifest: For the perpendiculars given do halfe them: And the halfes as before are equall.

15 Of unequall inscripts the diameter is the greatest: And that which is next to the diameter, is greater than that which is farther off from it: That which is farthest off from it, is the least: And that which is next to the least, is lesser than that which is farther off: And those two onely which are on each side of the diameter are equall è 15 e iij.

This proposition consisteth of five members: The first is, The diameter is the greatest inscript: The second, That which is next to the diameter is greater than that which is farther off: The third, That which is farthest off from the diameter is the least: The fourth, That next to the least is lesser, than that farther off: The fifth, That two onely on each side of the diameter are equall betweene themselves. All which are manifest, out of that same argument of equalitie, that is the center the beginning of decreasing, and the end of increasing. For looke how much farther off you goe from the center, or how much nearer you come unto it, so much lesser or greater doe you make the inscript.

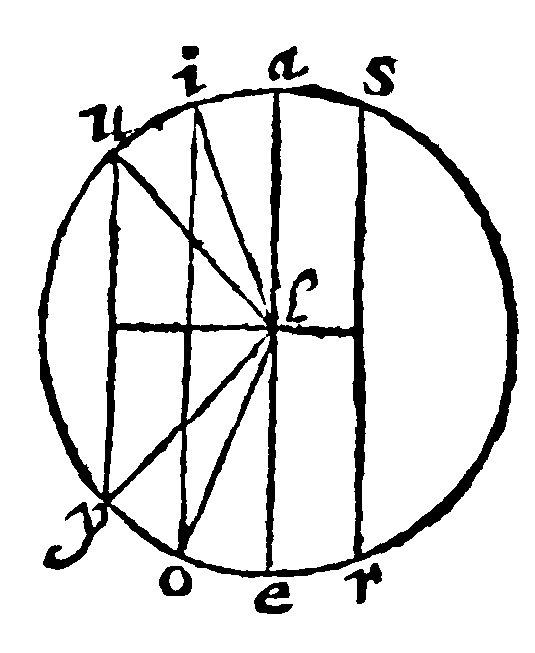
Let there be in a circle; many inscripts, of which one, to wit, ae, let it be the diameter: I say, that it is of them all the greatest or longest. But let io, be nearer to the diameter, (or as in the former Elements was said) nearer to the center, than uy. I say that io, is longer than uy. Moreover, let uy, be the farthest off from the same diameter or center; I say the same uy, is the shortest of them all. Now to this shortest uy, let io, be nearer than ae; I say therefore that io, also is lesser than ae. Let at length io, be not the diameter: I say that beyond the diameter ae, there may onely a line be inscribed equall unto it, such as is sr. And those equal betweene themselves on each side of the diametry may only be given, not three, nor more. And after the same manner also, onely one beyond the diameter, may possibly be equall to uy, to wit, that which is as farre off from the diameter as it is; and so in others.

But Euclides conclusion is by triangles of two sides greater than the other; and of the greater angle.

The first part is plaine thus: Because the diameter ae, is equall to il, and lo, viz. to the raies; And to those which are greater than io, the base by the 9. e vj &c.

The second part of the nearer, is manifest by the 5 e vij. because of the triangle ilo, equicrurall to the triangle uly, is greater in angle: And therefore it is also greater in base.

The third and fourth are consectaries of the first.

The fifth part is manifest by the second: For if beside io, and sr, there be supposed a third equall, the same also shall be unequall, because it shall be both nearer and farther off from the diameter.

16 Of right lines drawne from a point in the diameter which is not the center unto the periphery, that which passeth by the center is the greatest: And that which is nearer to the greatest, is greater than that which is farther off: The other part of the greatest is the left. And that which is nearest to the least, is lesser than that which is farther off: And two on each side of the greater or least are only equall. 7 p iij.

The first part of ae, and ai, is manifest, as before, by the 9 e vj. The second of ai, and ao; Item of ao, and au, is plaine by the 5 e vij.

The third, that ay, is lesser than au, because sy, which is equall to su, is lesser than the right lines sa, and au, by the 9 e vj: And the common sa, being taken away, ay shall be left, lesser than au.

The fourth part followeth of the third.

The fifth let it be thus: sr, making the angle asr, equall to the angle asu, the bases au, and ar, shall be equall by the 2 e vij. To these if the third be supposed to be equall, as al, it would follow by the 1 e vij. that the whole angle sa, should be equall to rsa, the particular angle, which is impossible. And out of this fifth part issueth this Consectary.

Therefore

17 If a point in a circle be the bound of three equall right lines determined in the periphery, it is the center of the circle. 9 p iij.

Let the point a, in a circle be the common bound of three right lines, ending in the periphery and equall betweene themselves, be ae, ai, au. I say this point is the center of the Circle.

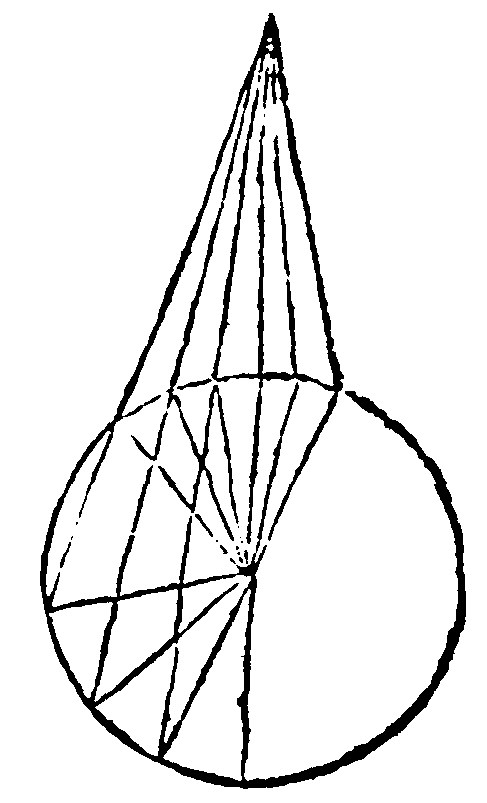
Otherwise from a point of the diameter which is not the center, not onely two right lines on each side should be equall. For by any point whatsoever the diameter may be drawne. Such was before observed in a quinquangle; If three angles be equall, all are equall; so in a Circle: If three right lines falling from the same point unto the perephery be equall, all are equall.

18 Of right lines drawne from a point assigned without the periphery, unto the concavity or hollow of the same, that which is by the center is the greatest; And that next to the greatest, is greater than that which is farther off: But of those which fall upon the convexitie of the circumference, the segment of the greatest is least. And that which is next unto the least is lesser than that is farther off: And two on each side of the greatest or least are onely equall. 8 p iij.

The demonstration of this is very like unto the above mentioned, of five parts. And thus much of the secants, the Tangents doe follow.

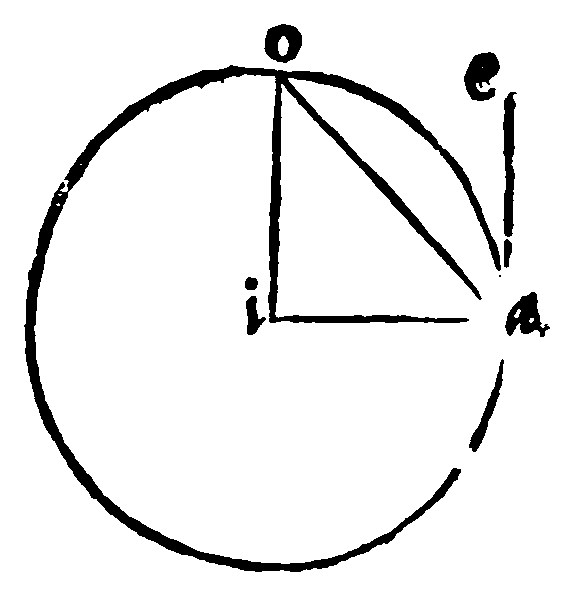
19 If a right line be perpendicular unto the end of the diameter, it doth touch the periphery: And contrariwise è 16 p iij.

As for example, Let the circle given ae, be perpendicular to the end of the diameter, or the end of the ray, in the end a, as suppose the ray be ia: I say, that ea, doth touch, not cut the periphery in the common bound a.

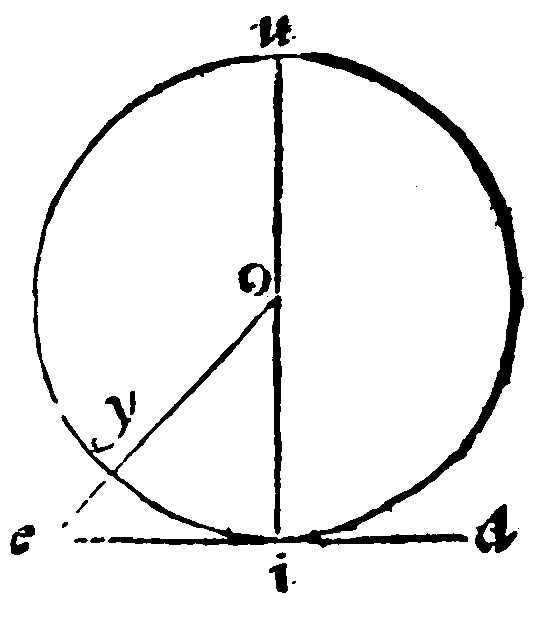
This was to have beene made a postulatum out of the definition of a perpendicle: Because if this should leane never so little, it should cut the periphery, and should not be perpendicular: Notwithstanding Euclide doth force it thus: Otherwise let the right line ae, be perpendicular to the diameter ai. And a right line from o, with the center i, let it fall within the circle at o, and let oi, joyned together. Here in the triangle aoi, two angles, contrary to the 13 e vj, should be right angles at a, by the grant: And at o, by the 17 e vj.

The demonstration of the converse is like unto the former. For if the tangent, or touch-line ae, be not perpendicular to the diameter iou, let oe, from the center o, be drawne perpendicular; Then shall the angle oei, be right angle: And oie an acutangle: And therefore by the 22 e vj, oi, that is oy, shall be greater then oye, that is the part, then the whole.

Therefore

20 If a right line doe passe by the center and touch-point, it is perpendicular to the tangent or touch-line. 18 p iij.

Or thus, as Schoner amendeth it: If a right line be the diameter by the touch point, it is perpendicular to the tangent.