The Way To Geometry

21 If a right line be perpendicular unto the tangent, it doth passe by the center and touch-point. 19. p iij.

Or thus: if it be perpendicular to the tangent, it is a diameter by the touch point: Schoner.

For a right line either from the center unto the touch-point; or from the touch point unto the center is radius or semidiameter.

And

22 The touch-point is that, into which the perpendicular from the center doth fall upon the touch line.

23 A tangent on the same side is onely one.

Or touch line is but one upon one, and the same side: H. Or. A tangent is but one onely in that point of the periphery Schoner.

It is a consectary drawne out of the xiij. e ij. Because a tangent is a very perpendicular.

Euclide propoundeth this more specially thus; that no other right line may possibly fall betweene the periphery and the tangent.

And

24 A touch-angle is lesser than any rectilineall acute angle, è 16 p ij.

Angulus contractus, A touch angle is an angle of a straight touch-line and a periphery. It is commonly called Angulus contingentiæ: Of Proclus it is named Cornicularis, an horne-like corner; because it is made of a right line and periphery like unto a horne. It is lesse therefore than any acute or sharpe right-lined angle: Because if it were not lesser, a right line might fall between the periphery and the perpendicular.

And

25 All touch-angles in equall peripheries are equall.

But in unequall peripheries, the cornicular angle of a lesser periphery, is greater than the Cornicular of a greater.

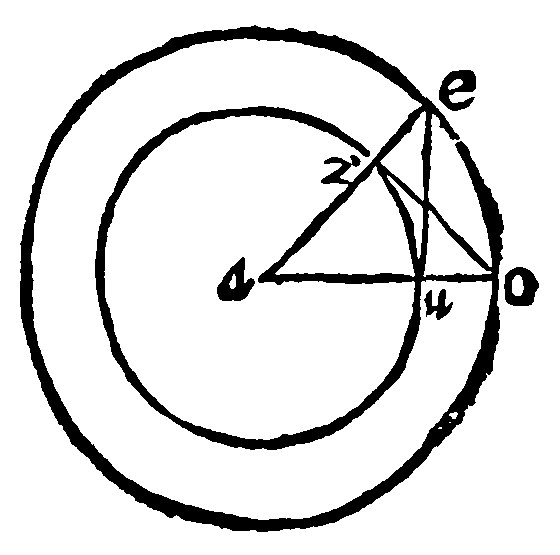
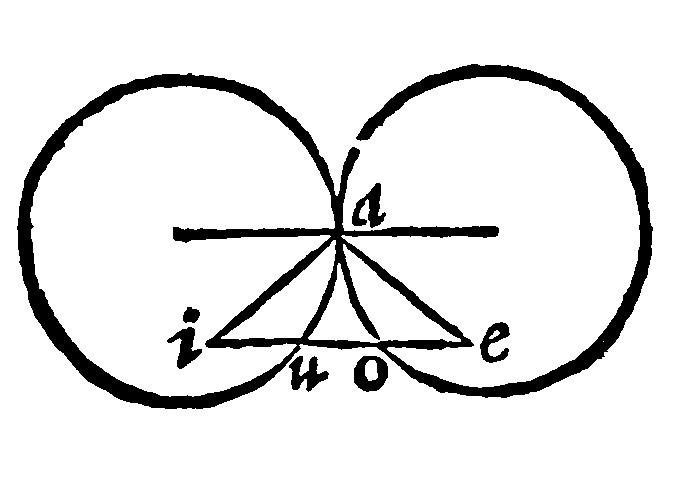
26 If from a ray out of the center of a periphery given, a periphery be described unto a point assigned without, and from the meeting of the assigned and the ray, a perpendicular falling upon the said ray unto the now described periphery, be tied by a right line with the said center, a right line drawne from the point given unto the meeting of the periphery given, and the knitting line shall touch the assigned periphery 17 p iij.

As with the ray ae, from the center a, of the periphery assigned, unto the point assigned e, let the periphery eo, be described: And let io, be perpendicular to the ray unto the described periphery. This knit by a right line unto the center a, let eu, be drawne. I say, that eu, doth touch the periphery iu, assigned: Because it shall be perpendicular unto the end of the diameter. For the triangles eau, and oai, by the 2 e vij, seeing they are equicrurall; And equall in shankes of the common angle; they are equall in the angles at the base. But the angle aio, is a right angle: Therefore the angle eua, shall be a right angle. And therefore the right line eu, by the 13 e ij, is perpendicular to ao.

Thus much of the Secants and Tangents severally: It followeth of both kindes joyntly together.

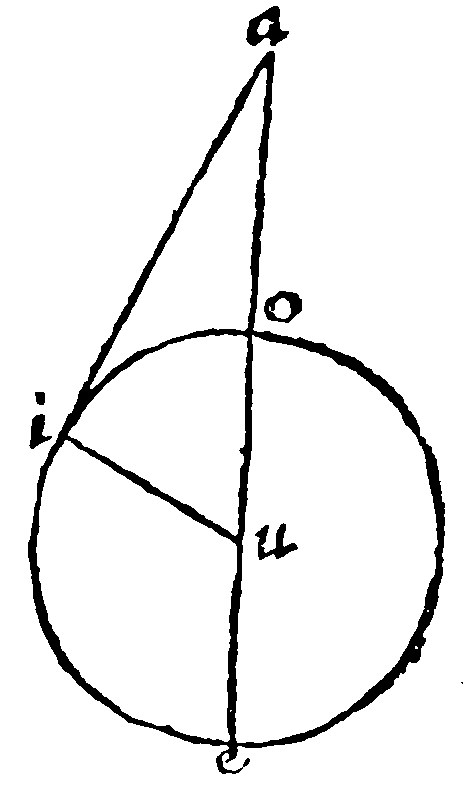
27 If of two right lines, from an assigned point without, the first doe cut a periphery unto the concave, the other do touch the same; the oblong of the secant, and of the outter segment of the secant, is equall to the quadrate of the tangent: and if such a like oblong be equall to the quadrate of the other, that same other doth touch the periphery: 36, and 37. p iij.

If the secant or cutting line do passe by the center, the matter is more easie and as here, Let ae, cut; And ai, touch: The outter segment is ao, and the center u, Now ui, shall be perpendicular to the tangent ai, by the 20. e: Then by 8 e xiij, the oblong of ea, and ao, with the quadrate of au, that is, of iu, is equall to the quadrate of au, that is, by the 9 e xij. to the quadrates of ai, and iu. Take iu, the common quadrate: The Rectangle shall be equall to the quadrate of the tangent.

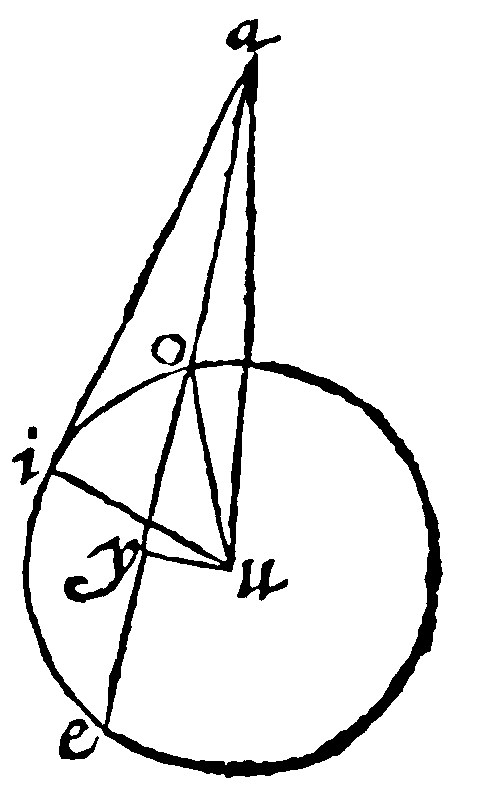
If the secant doe not passe by the center, as in this figure, the center u, found by the 7 e, iu, shall be by the 20 e perpendicular unto the tangent ai; then draw ua, and uo, and the perpendicular halving oe, by the 10 e. Here by the 8 e xiij, the oblong of ae, and ao, with the quadrate oy, is equal to the quadrate ay: Therefore yu, the common quadrate added, the same oblong, with the quadrates oy, and yu, that is by the 9 e xij. with the quadrate ou, is equall to the quadrates ay, and uy, that is, by the 9 e xij, to au, that is, againe, to ai, and iu. Lastly, let ur, and iu, two equall quadrates be taken from each, and there wil remaine the oblong equall to the quadrate of the tangent.

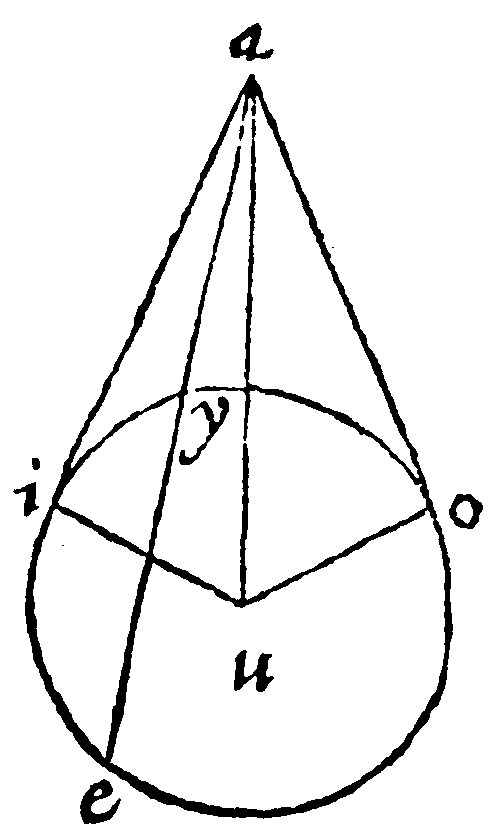
The converse is likewise demonstrated in this figure. Let the Rectangle of ae, and ay, be equall to the quadrate of ai. I say, that ai doth touch the circle. For let, by the 26 e, ao the tangent be drawne: Item let au, ui, and uo bee drawne. Here the oblong of ea, and ay, is equall to the quadrate of ao, by the 27 e: And to the quadrate of ai, by the grant. Therefore ai, and ao, are equall. Then is uo, by the 20 e, perpendicular to the tangent. Here the triangles auo, and aui, are equilaters: And by the 1 e vij, equiangles. But the angle at o is a right angle: Therefore also a right angle and equall to it is that at i, by the 13 e iij, wherefore ai is perpendicular to the end of the diameter: And, by the 19 e, it toucheth the periphery.

Therefore

28. All tangents falling from the same point are equall.

Or, Touch lines drawne from one and the same point are equall: H.

Because their quadrates are equall to the same oblong.

And

29. The oblongs made of any secant from the same point, and of the outter segment of the secant are equall betweene themselves. Camp. 36 p iij.

The reason is because to the same thing.

And

30. To two right lines given one may so continue or joyne the third, that the oblong of the continued and the continuation may be equall to the quadrate remaining. Vitellio 127 p j.

As in the first figure, if the first of the lines given be eo, the second ia, the third oa.

Now are we come to Circular Geometry, that is to the Geometry of Circles or Peripheries cut and touching one another: And of Right lines and Peripheries.

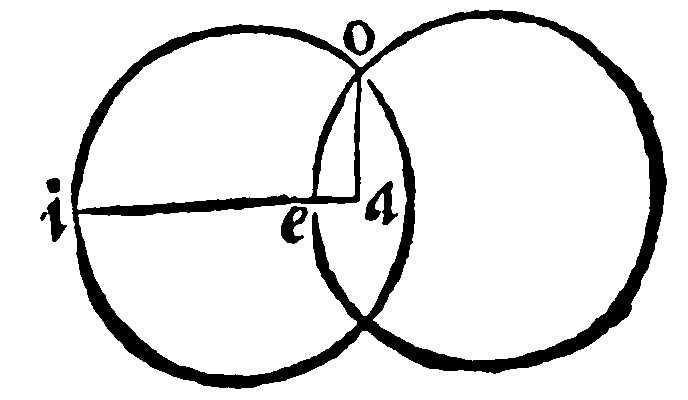
31. If peripheries doe either cut or touch one another, they are eccentrickes: And they doe cut one another in two points onely, and these by the touch point doe continue their diameters, 5. 6. 10, 11, 12 p iij.

All these might well have beene asked: But they have also their demonstrations, ex impossibili, not very difficult.

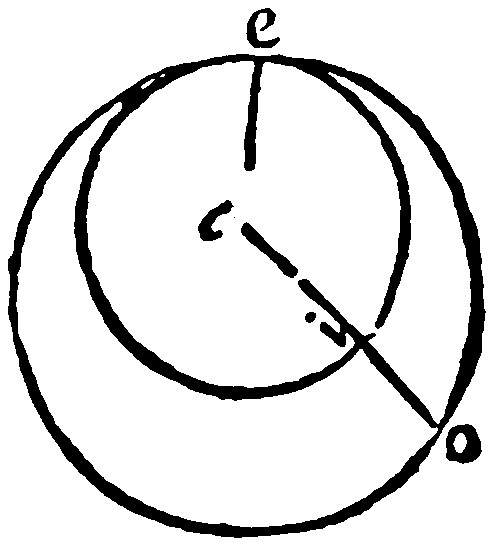
The first part is manifest, because the part should be equall to the whole, if the Center were the same to both, as a. For two raies are equall to the common raie ao: And therefore ae and ai, that is, the part and the whole, are equall one to another.

The second part is demonstrated as the first: For otherwise the part must be equall to the whole, as here ae and ai, the raies of the lesser periphery; And ae, and ao, the raies of the greater are equall. Wherefore ai, should be equall to ao the Part to the whole.

If the Peripheries be outwardly contiguall, the matter is more easie, and by the judgement of Euclide it deserved not a demonstration, as here.

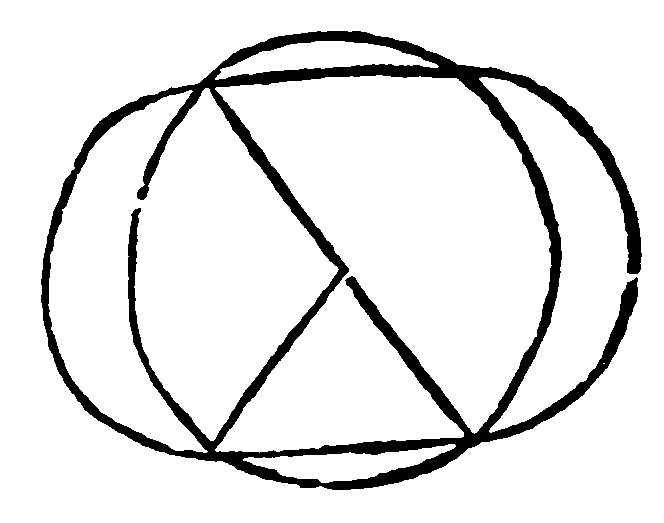
The third part is apparent out of the first: Otherwise those which cut one another should be concentrickes. For, by the 7 e, the center being found: And by the 9 e, three right lines being drawne from the center unto three points of the sections, the three raies must be equall, as here.

The fourth part is demonstrated after the same manner: Because otherwise the Part must be greater then the whole. For let the right line aeio, be drawne by the centers a and e: And let the particular raies be eu, and au. Here two sides ue, and ea, of the triangle uea, by the 9 e vj, are greater than ua: And therefore also then ao; Take away ae, the remainder ue, shall be greater than eo. But ei is equall to eu. Wherefore ei is greater than eo, the part, than the whole.

The same will fall out, if the touch be without, as here: For, by the 9 e vj, ea and ia, are greater than ie. But eo and iu, are equall to ea, and ia. Wherefore eo, and iu, are greater than ie, the parts than the whole.

Of right lines and Peripheries joyntly the rate is but one.

32. If inscripts be equall, they doe cut equall peripheries: And contrariwise, 28, 29 p iij.

Or thus: If the inscripts of the same circle or of equall circles be equall, they doe cut equall peripheries: And contrariwise B.

Or thus: If lines inscribed into equall circles or to the same be equall, they cut equall peripheries: And contrariwise, if they doe cut equall peripheries, they shall themselves be equall: Schoner.

The matter is apparent by congruency or application: as here in this example. For let the circles agree, and then shall equall inscripts and peripheries agree.

Except with the learned Rodulphus Snellius, you doe understand aswell two equall peripheries to be given, as two equall right lines, you shall not conclude two equall sections, and therefore we have justly inserted of the same, or of equall Circles; which we doe now see was in like manner by Lazarus Schonerus.

The sixteenth Booke of Geometry, Of the Segments of a Circle

1. A Segment of a Circle is that which is comprehended outterly of a periphery, and innerly of a right line.

The Geometry of Segments is common also to the spheare: But now this same generall is hard to be declared and taught: And the segment may be comprehended within of an oblique line either single or manifold. But here we follow those things that are usuall and commonly received. First therefore the generall definition is set formost, for the more easie distinguishing of the species and severall kindes.

2. A segment of a Circle is either a sectour, or a section.

Segmentum a segment, and Sectio a section, and Sector a sectour, are almost the same in common acceptation, but they shall be distinguished by their definitions.

3. A Sectour is a segment innerly comprehended of two right lines, making an angle in the center; which is called an angle in the center: As the periphery is, the base of the sectour, 9 d iij.

As aei is a sectour. Here a sectour is defined, and his right lined angle, is absolutely called The greater Sectour which notwithstanding may be cut into two sectours by drawing of a semidiameter, as after shall be seene in the measuring of a section.

4. An angle in the Periphery is an angle comprehended of two right lines inscribed, and jointly bounded or meeting in the periphery. 8 d iij.

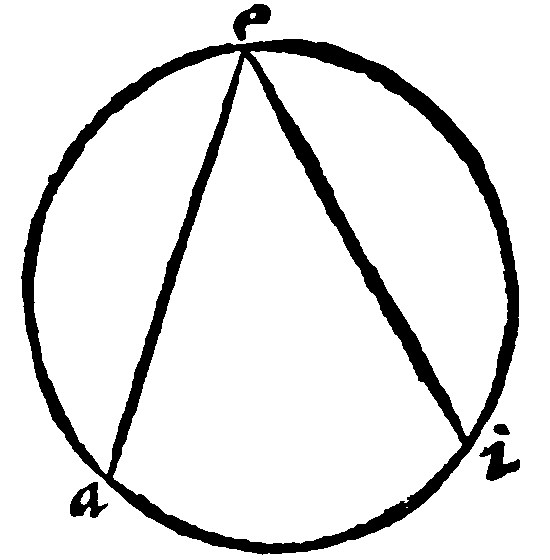
This might have beene called The Sectour in the Periphery, to wit, comprehended innerly of two right lines joyntly bounded in the periphery; as here aei.

5. The angle in the center, is double to the angle of the periphery standing upon the same base, 20 p iij.

The variety or the example in Euclide is threefold, and yet the demonstration is but one and the same: As here eai, the angle in the center, shall be prooved to be double to eoi, the angle in the periphery, the right line ou cutting it into two triangles on each side equicrurall; And, by the 17 e vj, at the base equiangles: Whose doubles severally are the angles, eau, of eoa: And iau, of ioa, For seeing it is equall to the two inner equall betweene themselves by the 15 e vj; it shall be the double of one of them. Therefore the whole eai, is the double of the whole eoi.

The second example is thus of the angle in the center aei: And in the periphery aoi. Here the shankes eo, and ei, by the 28 e iiij, are equall: And by the 17 e vj, the angles at o and i are equall: To both which the angle in the center is equall, by the 15 e vj. Therefore it is double of the one.

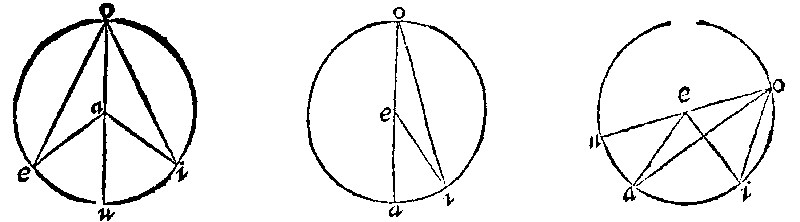
The third example is of the angle in the center, aei, And in the periphery aoi, Let the diameter be oeu. Here the whole angle ieu, by the 15 e vj, is equall to the two inner angles eoi, and eio, which are equall one to another, by the 17 e vj: And therefore it is double of the one. Item the particular angle aeu, is equall by the 15 e vj, to the angles eoa, and eao, equall also one to another, by the 17 e vj. Therefore the remainder aei, is the double of the other aoi, in the periphery.

Therefore

6. If the angle in the periphery be equall to the angle in the center, it is double to it in base. And contrariwise.

This followeth out of the former element: For the angle in the center is double to the angle in the periphery standing upon the same base: Wherefore if the angle in the periphery be to be made equall to the angle in the center, his base is to be doubled, and thence shall follow the equality of them both: S.

7. The angles in the center or periphery of equall circles, are as the Peripheries are upon which they doe insist: And contrariwise. è 33 p vj, and 26, 27 p iij.

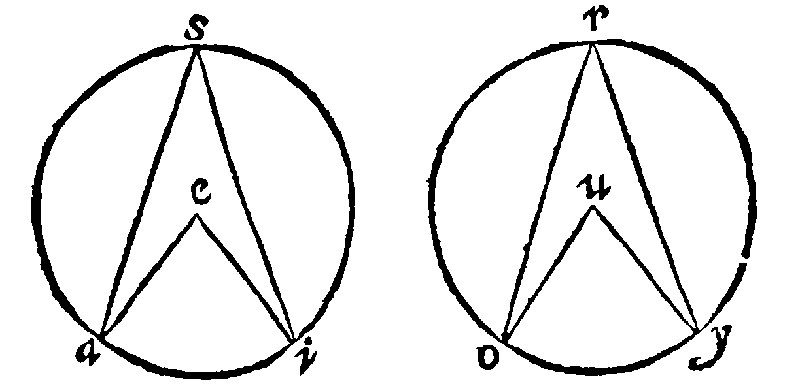
Here is a double proportion with the periphery underneath, of the angles in the center: And of angles in the periphery. But it shall suffice to declare it in the angles in the center.

First therefore let the Angles in the center aei, and ouy be equall: The bases ai, and oy, shall be equall, by the 11 e vij: And the peripheries, ai, and oy, by the 32 e xv, shall likewise be equall. Therefore if the angles be unequall, the peripheries likewise shall be unequall.

The same shall also be true of the Angles in the Periphery. The Converse in like manner is true: From whence followeth this consectary:

Therefore

8. As the sectour is unto the sectour, so is the angle unto the angle: And Contrariwise.

And thus much of the Sectour.

9. A section is a segment of a circle within cōprehended of one right line, which is termed the base of the section.

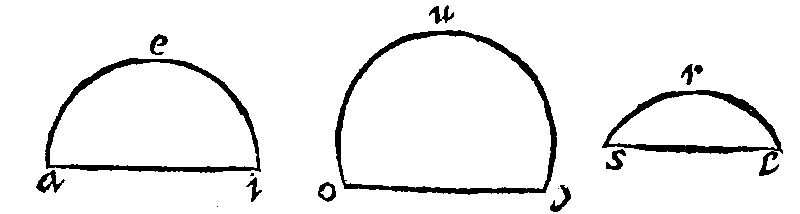
As here, aei, and ouy, and srl, are sections.

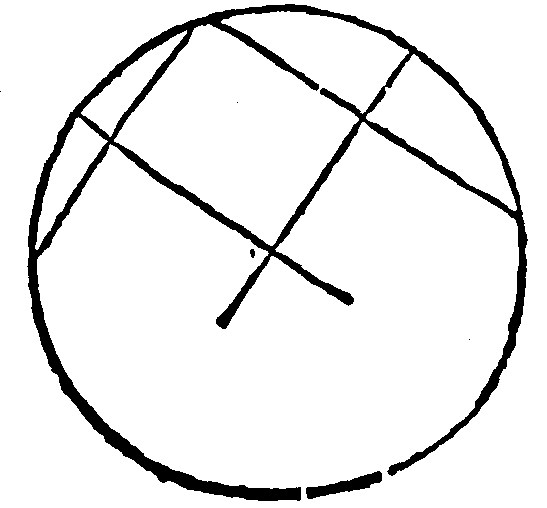
10. A section is made up by finding of the center.

The Invention of the center was manifest at the 7 e xv: And so here thou seest a way to make up a Circle, by the 8 e xv.

11 The periphery of a section is divided into two equall parts by a perpendicular dividing the base into two equall parts. 20. p iij.

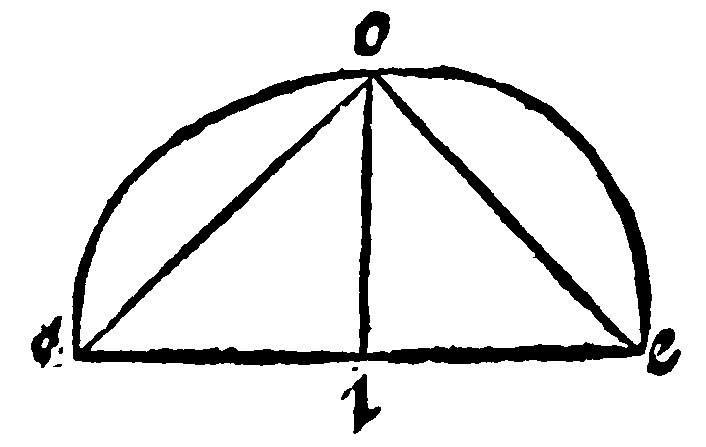
Let the periphery of the section aoe, to be halfed or cut into two equall parts. Let the base ae, be cut into two equall parts by the pendicular io, which shall cut the periphery in o, I say, that ao, and oe, are bisegments. For draw two right lines ao, and oe, and thou shalt have two triangles aio, and eio, equilaters by the 2 e vij. Therefore the bases ao, and oe, are equall: And by the 32. e xv. equall peripheries to the subtenses.

Here Euclide doth by congruency comprehende two peripheries in one, and so doe we comprehend them.

12 An angle in a section is an angle comprehended of two right lines joyntly bounded in the base and in the periphery joyntly bounded 7 d iij.

Or thus: An angle in the section, is an angle comprehended under two right lines, having the same tearmes with the bases, and the termes with the circumference: H. As aoe, in the former example.

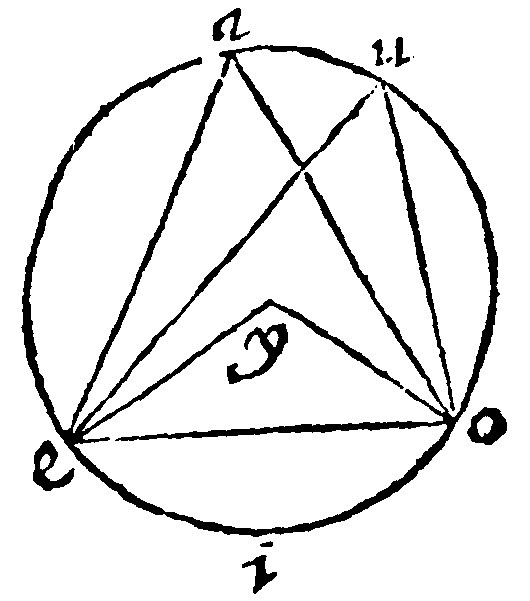
13 The angles in the same section are equall. 21. p iij.

Let the section be eauo, And in it the angles at a, & u: These are equall, because, by the 5 e, they are the halfes of the angle eyo, in the center: Or else they are equall, by the 7 e, because they insist upon the same periphery.

Here it is certaine that angles in a section are indeed angles in a periphery, and doe differ onely in base.

14 The angles in opposite sections are equall to two right angles. 22. p iij.

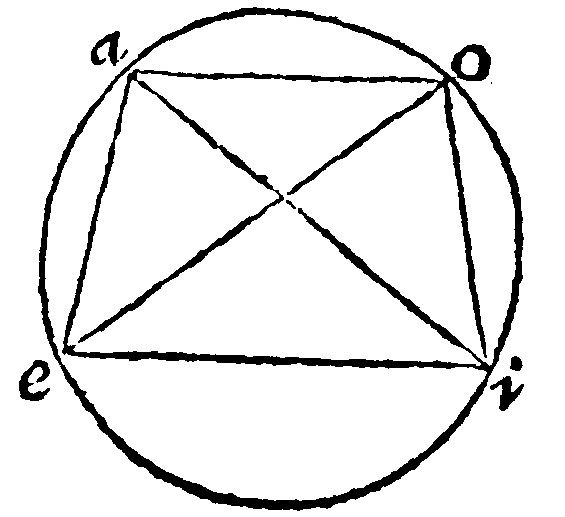
For here the opposite angles at a, and i, are equall to the three angles of the triangle eoi, which are equall to two right angles, by the 13 e vj. For first i, is equall to it selfe: Then a, by parts is equall to the two other. For eai, is equall to eoi, and iao, to oei, by the 13 e. Therefore the opposite angles are equall to two right angles.

The reason or rate of a section is thus: The similitude doth follow.

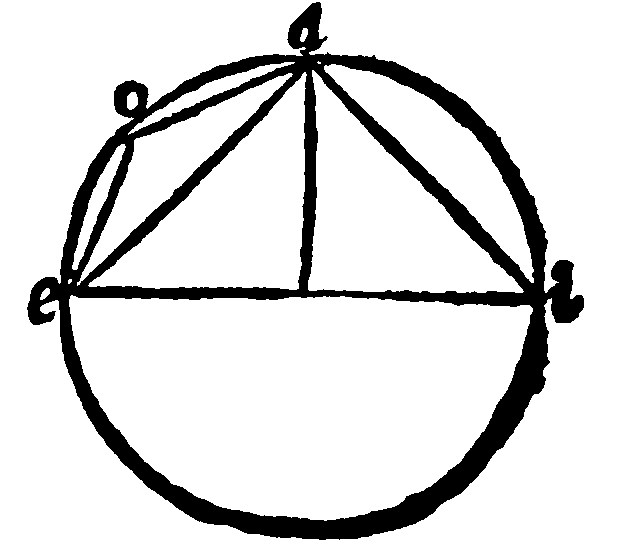
15 If sections doe receive [or containe] equall angles, they are alike è 10. d iij.

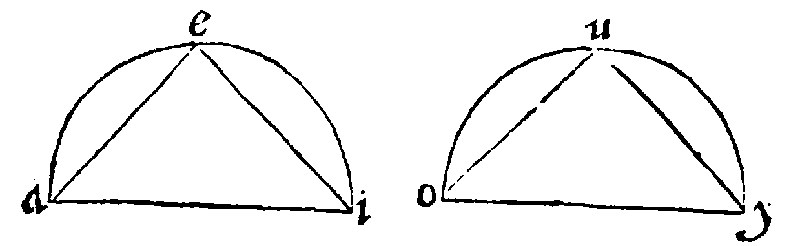
As here aei, and ouy. The triangle here inscribed, seeing they are equiangles, by the grant; they shall also be alike, by the 12 e vij.

16 If like sections be upon an equall base, they are equall: and contrariwise. 23, 24. p iij.

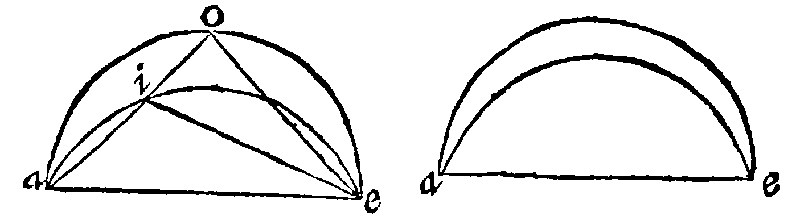
In the first figure, let the base be the same. And if they shall be said to unequall sections; and one of them greater than another, the angle in that aoe, shall be lesse than the angle aie, in the lesser section, by the 16 e vj. which notwithstanding, by the grant, is equall.

In the second figure, if one section be put upon another, it will agree with it: Otherwise against the first part, like sections upon the same base, should not be equall. But congruency is here sufficient.

By the former two propositions, and by the 9 e xv. one may finde a section like unto another assigned, or else from a circle given to cut off one like unto it.

17 Angle of a section is that which is comprehended of the bounds of a section.

As here eai: And eia.

18 A section is either a semicircle: or that which is unequall to a semicircle.

A section is two fold, a semicircle, to wit, when it is cut by the diameter: or unequall to a semicircle, when it is cut by a line lesser than the diameter.

19 A semicircle is the half section of a circle.

Or it is that which is made the diameter.

Therefore

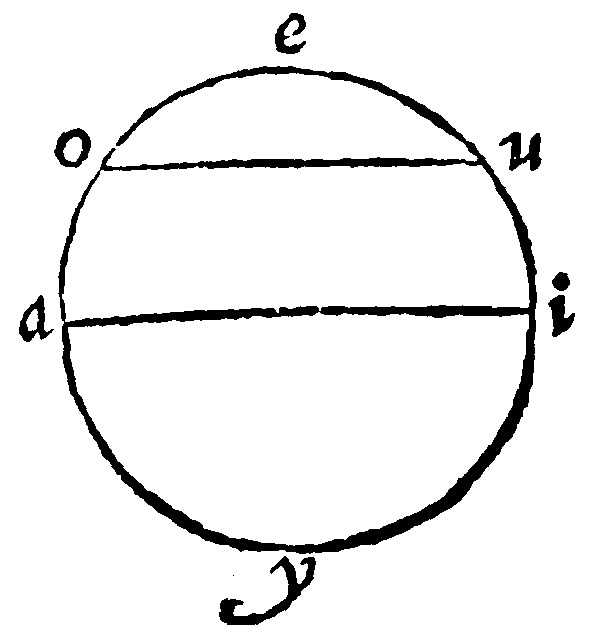
20 A semicircle is comprehended of a periphery and the diameter 18 d j.

As aei, is a semicircle: The other sections, as oyu, and oeu, are unequall sections: that greater; this lesser.

21 The angle in a semicircle is a right angle: The angle of a semicircle is lesser than a rectilineall right angle: But greater than any acute angle: The angle in a greater section is lesser than a right angle: Of a greater, it is a greater. In a lesser it is greater: Of a lesser, it is lesser, è 31. and 16. p iij.

Or thus: The angle in a semicircle is a right angle, the angle of a semicircle is lesse than a right rightlined angle, but greater than any acute angle: The angle in the greater section is lesse than a right angle: the angle of the greater section is greater than a right angle: the angle in the lesser section is greater than a right angle, the angle of the lesser section, is lesser than a right angle: H.

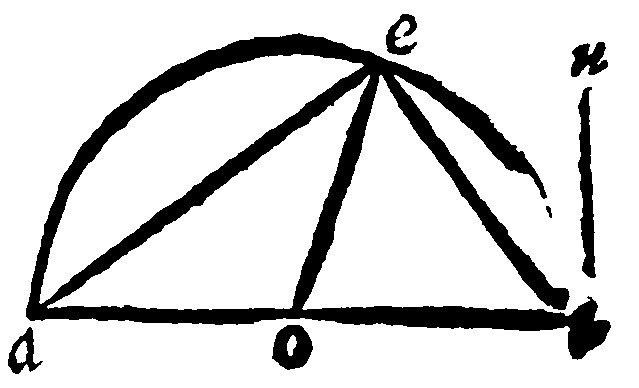
There are seven parts of this Element: The first is that The angle in a semicircle is a right angle: as in aei: For if the ray oe, be drawne, the angle aei, shall be divided into two angles aeo, and oei, equall to the angles eao, and eio, by the 17 e vj. Therefore seeing that one angle is equall to the other two, it is a right angle, by the 6 e viij. Aristotle saith that the angle in a semicircle is a right angle, because it is the halfe of two right angles, which is all one in effect.

The second part, That the angle of a semicircle is lesser than a right angle; is manifest out of that, because it is the part of a right angle. For the angle of the semicircle aie, is part of the rectilineall right angle aiu.

The third part, That it is greater than any acute angle; is manifest out of the 23. e xv. For otherwise a tangent were not on the same part one onely and no more.

The fourth part is thus made manifest: The angle at i, in the greater section aei, is lesser than a right angle; because it is in the same triangle aei, which at a, is a right angle. And if neither of the shankes be by the center, not withstanding an angle may be made equall to the assigned in the same section.

The fifth is thus: The angle of the greater section eai, is greater than a right angle: because it containeth a right-angle.

The sixth is thus, the angle aoe, in a lesser section, is greater than a right angle, by the 14 e xvj. Because that which is in the opposite section, is lesser than a right angle.