Формирование универсальных учебных действий у младших школьников с нарушением слуха. 2-е издание

2.3. Технология обучения детей с нарушением слуха рассуждению

Активное осуществление учебной деятельности приводит к значительным изменениям в личностном и умственном развитии школьников (Д. Б. Эльконин, В. В. Давыдов, А. К. Маркова, Л. И. Айдарова). Исследования в области сурдопедагогики и сурдопсихологии (А. И. Дьячков, С. А. Зыков, А. П. Гозова, Т. В. Розанова, Л. И. Тигранова, Ж. И. Шиф, Н. В. Яшкова и другие) свидетельствуют о больших резервах умственного развития детей с недостатками слуха.

Цель настоящей главы состоит в рассмотрении дополнительных возможностей развития логических суждений глухих и слабослышащих детей младшего школьного возраста в процессе учебной деятельности. Конкретные задачи исследования заключаются в выделении основных этапов развития логических рассуждений, рассмотрении некоторых путей, методов и приемов формирования умения рассуждать, апробации их в процессе экспериментального обучения и выявления эффективности для повышения уровня дискурсивного мышления детей с недостатками слуха.

Развитие рассуждающего мышления, умения адекватно отражать логические отношения в речи необходимо начинать с первых дней обучения в школе. В соответствии с теорией поэтапного формирования умственных действий и с учетом особенностей развития глухих и слабослышащих детей мы выделили пять этапов обучения рассуждению. Первый этап – пропедевтический. Дети приобретают опыт речевого общения с окружающими, друг с другом в процессе решения практических задач. Речь, выступая в качестве средства общения, включается и в механизм интеллектуальной деятельности, позволяющей выполнять отвлечения, обобщения, рассуждения. На этом этапе школьники обучаются умственным действиям, овладение которыми позволяет логически правильно осуществлять рассуждения, а именно: вычленению определенных свойств, сведений, соотнесению их между собой, фиксации существенных связей, выделению условий и обстоятельств действий и усвоению их объективного значения.

На втором этапе составляется схема ориентировки в объективных условиях действия с целью его успешного выполнения. Дети должны ознакомиться с понятием «рассуждение», с его структурно-смысловыми частями, закономерностями использования.

На третьем этапе учащиеся знакомятся с различными способами логических рассуждений в процессе решения учебных задач, обучаясь при этом устанавливать логические связи между предметами, явлениями, событиями, действиями, используя наглядные опоры. Этот этап (материального, или материализованного, действия – по П. Я. Гальперину) имеет особенное значение в обучении всех детей с особыми образовательными потребностями, в частности с нарушениями слуха.

На четвертом этапе ученики самостоятельно проводят рассуждения во внешнеречевой форме в соответствии с усвоенными алгоритмическими предписаниями без опоры на вспомогательные средства. Главное внимание при этом следует уделять активному оперированию речевыми средствами, выражающими различные логические отношения. Логическое рассуждение превращается в общий способ мыслительной деятельности, который используется учащимися как метод учебной деятельности.

На пятом, завершающем, этапе ученики должны не только правильно понимать и использовать логические рассуждения, но и осуществлять перенос усвоенного в другие ситуации, в другие области знаний. Здесь наблюдается активная деятельность самих школьников, сопоставление и перестраивание логических рассуждений.

Перейдем к рассмотрению конкретных педагогических путей, методов и приемов обучения рассуждению, которые использовались в настоящей работе.

На начальных этапах обучения работа строилась на конкретном, доступном материале. Упражнения были направлены на практическое овладение простейшими рассуждениями и приводили к раскрытию смысла логических понятий и действий. Логические действия отрабатывались на разнообразном материале – русский язык, математика, ознакомление с окружающим миром, природоведение, предметно-практическое обучение (ППО), социально-бытовая ориентировка, игры.

В качестве примера приведем уроки деятельности (ППО). На уроках ППО школьники учатся устанавливать логические связи (временные, пространственные, причинно-следственные и т. д.) при наличии реальных наглядных отношений, выделяемых, прежде всего, в собственной практической деятельности. На первом этапе обучения учащиеся констатируют логические связи, аргументируя уже выполненные действия. Например, отчитываясь о деятельности, ребенок обобщает: «Сначала я слепил туловище, потом голову…», а обосновывая выбор картинок для аппликации, сообщает педагогу: «Это бывает летом». Сначала дети сопровождают свои практические действия речью: индивидуальным и хоровым проговариванием (наиболее существенных моментов деятельности). По мере развития основных мыслительных операций (анализа, синтеза, сравнения, обобщения) логическое рассуждение начинает предшествовать предметно-практической деятельности, предварять ее, вначале с опорой на наглядно представленный образец изделия, предметные карты, рисунок, а затем и без них. В 1–2 классах учащиеся выполняли такие задания, позволяющие строить рассуждения:

– Самостоятельное определение темы урока по приготовленному оборудованию: «Будем лепить, потому что на столе лежит пластилин».

– Определение организационных форм работы: «По-моему, мы будем работать парами, потому что у меня бумага, а у Саши карандаш и ножницы», «…потому что мозаику раздали одну на двоих».

– Обоснование выбора материалов для работы: «Мне нужен оранжевый пластилин, потому что я буду лепить лису», «Я буду делать черного котенка, дайте мне, пожалуйста, черную, а не белую бумагу».

Подобные виды работ направлены на развитие умения наблюдать, сравнивать, обобщать, устанавливать причинно-следственные связи и выражать логические отношения в речи. По мере развития активной речи дети начинали строить рассуждения на основе словесного материала:

– при отгадывании загадок: «Рыжая, хитрая, хвост длинный, пушистый. Живет в лесу, в норе. Кто это? Кого будем лепить?»;

– при решении логических задач: «Перевозит по воде людей и грузы. Есть мотор. Он больше, чем лодка, но меньше, чем теплоход. Что будем делать?»;

– при угадывании объекта деятельности с помощью вопросов, задаваемых учителю: «Какого цвета, формы, размера? Из каких частей состоит? Из какого материала сделан? Для чего он нужен? Как используется?»;

– при решении задач с избыточными и недостающими данными, например, при анализе готовой заявки определяется достаточность указанных материалов и инструментов;

– при придумывании для изготовления предмета, наиболее похожего или непохожего на образец.

Таким образом, на уроках ППО обучение сначала происходит на основе анализа наглядных ситуаций и собственных практических действий, затем на основе представлений о них, что обеспечивает поэтапное формирование умения рассуждать. Овладение учащимися рассуждением позволяло перейти к формированию умения доказывать, обосновывать свое мнение. С этой целью в речевую деятельность вначале вводился вопрос «Как ты думаешь?» и давалась форма ответа: «Я думаю, Сашу можно выбрать бригадиром», «Я думаю, что…», «Я думаю также (по-другому)», «Я согласна с мнением Вани!». Затем используется вопрос «Почему ты так думаешь?». Учащимся объяснялось, что при высказывании нужно доказывать свою точку зрения, и предлагался образец ответа: «Я так думаю, потому что…». Впоследствии вводилось понятие о том, что не все мнения могут быть одинаковыми, давалось понятие о споре, и предлагались фразы вежливого обращения к собеседнику: «Я думаю, что ты неправ, потому что…», «Мне кажется, что ты ошибаешься, так как…».

Для формирования умения рассуждать большое значение имеет организация действий детей с моделями, схемами, алгоритмическими предписаниями, которые играют роль внешней опоры для умственных действий. Полный набор ориентиров обеспечивает возможность самостоятельного контроля учащимися выполнения умственного действия на каждом этапе его формирования, а также успешное формирование как специальных умений и навыков, так и общеучебных. Алгоритмические предписания могут быть даны в виде материализованных таблиц, учебных, в том числе предметных, карт, памяток, которые выступают орудием, планом для действия и для рассуждения.

В процессе экспериментального обучения мы знакомили глухих и слабослышащих второклассников со структурной моделью рассуждения в двух формах (см. схему 1).

Схема 1

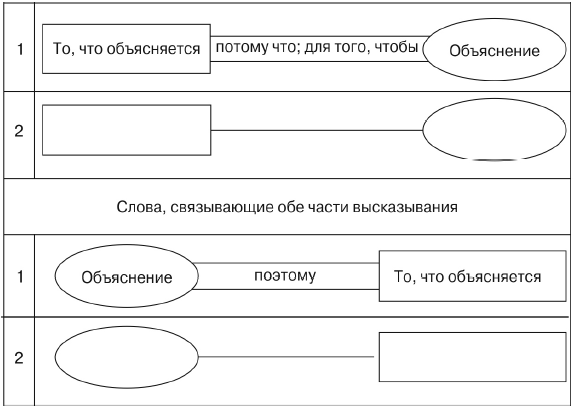
В качестве материала для отработки моделей рассуждений использовались, прежде всего, речевые высказывания, связанные с подготовкой, организацией или оценкой предметно-практической деятельности учащихся: «Мне нужны ножницы, чтобы вырезать круг»; «Аппликация выполнена красиво и аккуратно, поэтому мы возьмем ее на выставку»; «Я буду делать дом из пластилина, потому что я люблю работать с пластилином»; «В рассказе три части, поэтому будем делать три аппликации»; «Для того чтобы сделать макет, сначала нужно нарисовать эскиз» и т. д.

Для усвоения речевых конструкций рассуждений на уроках ППО была особым образом организована работа парами. Один ученик выполнял задание, второй выступал в роли «контролера», поправляя его, возражая. При этом он задавал вопрос: «Почему (для чего) ты так делаешь?». Отвечая на вопрос, первый ученик ориентировался на заданную схему рассуждения. Аналогично организовывалось взаимодействие в парах при составлении плана работы. «Контролер» предлагал вопросы, требующие объяснения, обоснования выбранной последовательности работы.

На уроках развития речи для усвоения моделей высказывания образец рассуждения соотносился со схемой; формулировались вопросы к частям высказывания; к определенной конструкции подбирались высказывания, для данных рассуждений самостоятельно строились модели. Последний вид работы оказался наиболее эффективным для овладения моделями рассуждений, что согласуется с данными других авторов (Н. Г. Салмина, 1981, с. 105). Для закрепления предлагалось из двух рассуждений выбрать верное, из частей высказываний составить рассуждения, для данной причины придумать возможные следствия и наоборот.

На уроках математики нами широко применялись алгоритмизированные схемы, отражающие ход рассуждения при решении того или иного примера, задачи. Пример (3 класс):

500 – 240 =?

500 – (200 + 40) = (сначала надо разложить вычитаемое на сотни и десятки).

(500 – 200) – 40 = (потом вычесть сотни из сотен).

300 – 40 = 260 (наконец, надо вычесть десятки).

Использование алгоритмов предполагает и самостоятельное их выведение в процессе решения различного рода задач.

На уроках ППО, русского языка использовались таблицы для формирования грамматических стереотипов, способов построения словосочетаний и т. п. Примеры (1–2 классы):

Подготовительный – 1 классы:

Подобные модели вывешиваются в классе и предлагаются учащимся в качестве опоры при сообщениях о своей деятельности, выражении просьбы и т. п.

Для формирования умения рассуждать в экспериментальной работе использовался также метод комментированного управления, когда один ученик ведет комментирование письма, разбора предложения по членам предложения, решения примера, задачи, а остальные работают по программе ведущего. Этот метод получил распространение в массовой школе (С. Н. Лысенкова, 1988). На современном этапе при наличии качественной звукоусиливающей аппаратуры создаются благоприятные условия для использования комментированного управления в школе для глухих и слабослышащих детей.

Так, например, решается пример: 15 – 8 = 15 – (5 + 3) = 15 – 5–3 = 10 – 3 = 7. Ученица пишет и одновременно рассуждает, все пишут вместе с ней.

Ученица: «Пишу 15 минус 8 равно. Заменю число 8 суммой удобных слагаемых 5 и 3. Получился пример: 15 минус в скобках 5 плюс 3 равно» и т. д.

Начинать обучать комментированию глухих детей целесообразно на уроках ППО. Сначала при фронтальной работе учитель побуждает ребенка к комментированию: «Расскажи ребятам, что ты делаешь? Как ты раскрашиваешь пингвина?» и поощряет его речевые высказывания. Затем при работе парами один ученик, ведущий, дает поручения («сложи лист бумаги пополам»), а другой их выполняет, комментируя свои действия («я складываю лист бумаги пополам»).

По мере усвоения комментируемое управление переходило в доказательное комментирование – рассуждение при решении задач, примеров, выполнении грамматических заданий с обоснованием решения.

Решается пример: 34 + 2 =

Ученик: Сначала я раскладываю число 34 на сумму разрядных слагаемых – 30 и 4 (пишет). Удобнее к 4 прибавить 2 и прибавить 30 (пишет). К 30 прибавить 6, получится 36 (пишет).

Учитель: Почему удобнее к 4 прибавить 2?

Ученик: Потому что единицы складываются с единицами.

По мере того как шел процесс комментирования, дети становились собраннее, внимательнее следили за ходом рассуждения ведущего, учились записывать за ним и исправлять ошибки (рассуждения каждого ведущего анализировались).

Благоприятные возможности для развития рассуждающего мышления создаются при решении арифметических задач. При анализе условий задачи словесный разбор производился с использованием предметной наглядности, рисунков, графических схем, краткой записи. Такая материализация текста задач обнажает существенные связи, переносит их в зрительный план и тем самым облегчает построение рассуждений. Внимание акцентировалось на заданиях следующего типа: – доказательство выбора действия («Выполняю сложение, потому что искомое число на… больше»);

– постановка возможных вопросов к задаче («У Андрюши было, 2 флажка, а у Ани 4» – Какие вопросы можно поставить?);

– составление условий к вопросу («Сколько карандашей у Коли?» – Какие условия можно придумать к этому вопросу?);

– составление задач по числовому выражению;

– перефразирование задачи. Учащиеся при этом получают обратную задачу, решение которой аналогично решению прямой задачи, положенной в основу. Например, задача: «Коля слепил 5 грибов, а Таня на 2 гриба меньше. Сколько всего грибов слепили дети?». Условие обратной задачи: «Таня слепила 3 гриба, а Коля на 2 гриба больше». При составлении обратной задачи дети рассуждают так: «Если Таня слепила на 2 гриба меньше, значит, Коля слепил на 2 гриба больше…».

Значимость аналогичных заданий в целях развития обратимости мыслительных действий подчеркивает и Т. В. Розанова (1978, 1985). Задания такого типа мы давали детям сначала на уроках ППО, где создаются для этого адекватные предметные ситуации. Например, после оценки количества изделий, выполненных каждой из двух бригад, предлагалось составить условия прямой и обратной задачи, придумать возможные вопросы.

Большое внимание в экспериментальной работе уделялось варьированию задачи по логическим моментам (с лишними, недостающими данными и т. д.). Так, при решении задач с недостающими («У Мити были конфеты. Он дал 3 конфеты Сереже. Сколько конфет осталось у Мити?») и избыточными данными («В шкафу лежало 8 ложек, 4 вилки и 2 ножа. Сколько ложек и ножей в шкафу?») возрастает уровень логической аргументации. Проводя анализ условий задачи, учащиеся определяли их достаточность и выявляли их связь с вопросом и между собой. При этом формируется умение обосновывать:

– почему нельзя решить задачу;

– почему это лишнее в условии;

– как надо изменить условия, чтобы ответить на вопрос задачи.

Предлагаемые задания способствовали преодолению шаблонных подходов к решению задач, когда последовательность чисел в тексте задачи, отдельные слова служат показателями искомого способа решения (Т. В. Розанова, 1978).

При решении каждой задачи от учеников сначала требуется отчет о ходе решения, а затем и аргументация способов решения.

Рассмотренные виды работ направлены на активизацию мыслительной деятельности и формирование умения рассуждать у детей с недостатками слуха.

На уроках чтения в ходе экспериментальной работы использовались задания, требующие умозаключений на основе текста. Так, при ознакомлении с жанрами произведений детей спрашивали, что они прочитали (сказку, стихотворение, рассказ), почему они думают, что это рассказ, а не сказка или стихотворение. При анализе произведений главное внимание уделялось выяснению понимания детьми основного смысла, нравственной сущности, а не внешней канвы произведения. Вопросы задавались разнообразные:

– О чем (о ком) говорится в произведении?

– Что произошло и почему?

– Что нового (интересного) узнали?

– Что можете рассказать о герое сказки?

– Что можете рассказать об остальных?

– Какие они?

– Докажите (обоснуйте) свое мнение.

– О чем говорит поступок главного героя?

– Какое событие главное в этом рассказе и почему?

Большое внимание уделялось определению причины события, цели действия («Зачем Гринька полез на березу?»), возможного следствия событий («Дождется ли зайчишка дедушку, как вы думаете?»), причинного объяснения возможного следствия («Почему нельзя разорять птичьи гнезда?»). Дети выполняли творческие задания на подбор синонимов, антонимов, образных определений. При этом им предлагалось не просто придумать определение, но и подумать, где его можно употребить; давались задания обобщающего характера: сравнить героев прочитанных произведений; широко практиковалось отгадывание и загадывание загадок.

Перечисленные, а также ряд других видов работ, используемых в современной системе обучения чтению, можно отнести к творческим, способствующим формированию развернутых рассуждений у глухих и слабослышащих детей.

Экспериментальная работа проводилась нами с разным контингентом детей (1–4 классы) на протяжении ряда лет. Рассмотренные методы и приемы развития рассуждающего мышления (использование алгоритмических предписаний в виде таблиц, схем, комментированное управление при решении примеров, задач, выполнении грамматических заданий, широкое использование логических задач и других творческих видов работ) апробировались как в школе для глухих, так и в школе для слабослышащих детей. Целенаправленная систематическая работа в целях выявления эффективности предлагаемых путей и методов обучения для развития рассуждения велась с двумя контингентами детей (2 классы школы глухих – 12 человек, 2 классы школы слабослышащих – 16 человек) на протяжении трех месяцев в рамках школьной программы. Констатирующий и контрольный эксперименты проводились с использованием методики, предложенной Л. И. Тиграновой (1978). Выявлялся уровень логических рассуждений детей на основе владения такими приемами логического мышления, как анализ, отвлечение, обобщение, классификация.

Успешность выполнения учащимися логических действий отражена в табл. 1. Ответы учащихся делились на три группы в зависимости от того, выполнялись действия самостоятельно или оказывалась помощь (первый вид помощи – дополнительный показ, второй вид – объяснение принципа решения).

Таблица 1

Успешность выполнения учащимися логических действий (в %)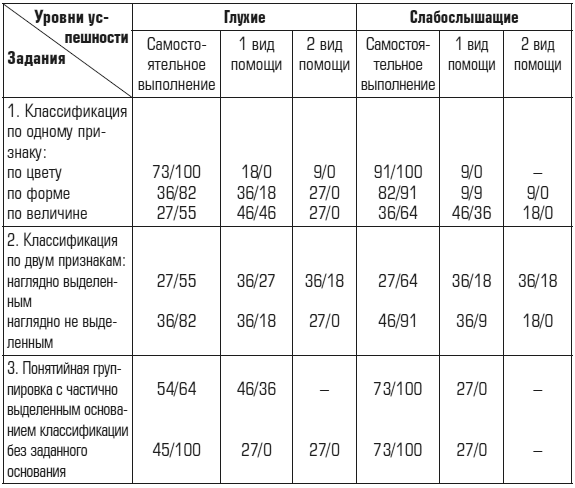

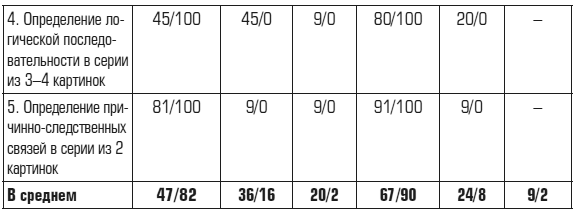
Примечание. Здесь и далее в таблицах первая цифра означает результат до начала обучения, вторая – после.

Как видно из табл. 1, в результате обучения у испытуемых (и у слабослышащих, и у глухих детей) значительно повысился уровень овладения основными логическими операциями. Особенно заметно выросла степень самостоятельности действий.

При оценке возможностей детей строить рассуждения было выделено четыре группы ответов (табл. 2).

– Правильно оформленное рассуждение с использованием: а) словесных обобщений и терминологии (например, ответ о принципах классификации по цвету: «Потому что эти фигуры одинаковые по цвету»); б) конкретных обозначений признаков («Потому что они одинаково желтые, одинаково красные»).

– Рассуждения в менее развернутой форме («Здесь желтые и здесь желтые – одинаково»).

– Отрывочные, отдельные слова, жесты (показывает желтые круг, квадрат, говорит: «Одинаково»).

– Ошибки, отсутствие ответа.

Таблица 2

Уровни логических рассуждений учащихся при выполнении действий классификации (в %)

Как свидетельствуют результаты (табл. 2), после экспериментального обучения возможности детей строить рассуждения значительно возросли, причем учащиеся в своих рассуждениях начали активно использовать обобщения и терминологическую лексику. Более высокий уровень рассуждений отмечался у слабослышащих детей в сравнении с глухими.

По результатам проверки возможностей установления логической последовательности событий и причинно-следственных связей было выделено три группы ответов (табл. 3):

Таблица 3

Уровни рассуждений учащихся при установлении причинно-следственных связей и логической последовательности событий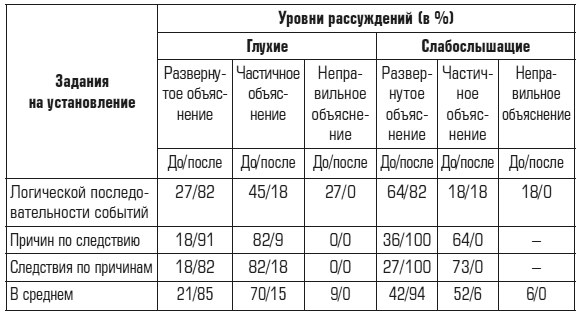

Данные, представленные в табл. 3, показывают, что дети, прошедшие специальное обучение, успешно справляются с заданиями. В своих рассказах они не просто описывают ход событий, но и устанавливают необходимые причинно-следственные отношения между их отдельными звеньями.

После экспериментального обучения речь учащихся во многих случаях начинает опережать практические действия, планируя и направляя их, то есть учащиеся до выполнения практических действий словесно обобщают представленные группы. Осознанное обобщение в речи способа решения облегчает выполнение заданий, делает их устойчиво правильными.

В заключение отметим, что программы специальных (коррекционных) общеобразовательных школ I и II вида представляют большой материал для умений оперировать понятиями, строить суждения, умозаключения, доказательства по типу развернутых рассуждений. При этом важно специально обучать детей построению суждений, умозаключений, знакомить с разными структурами и способами рассуждений.

Большое значение при обучении рассуждению имеют уроки предметно-практического обучения, ознакомления с окружающим миром, социально-бытовой ориентировки, на которых дети овладевают логическими суждениями, умозаключениями на основе наглядных связей, выделяемых, прежде всего, в собственной практической деятельности.

Рассмотренные в работе педагогические пути, методы, приемы, требующие обоснований, умозаключений, развернутых рассуждений, способствуют эффективному развитию дискурсивного мышления детей с недостатками слуха.

2.4. Развитие мышления в процессе логических игр

Развитие логического мышления детей – необходимое условие успешного обучения. В настоящее время общепризнана необходимость проведения специальной работы по развитию логического мышления детей в процессе учебной деятельности (П. Я. Гальперин, Н. Н. Поддьяков, В. В. Давыдов; в сурдопедагогике: Т. В. Розанова, Л. И. Тигранова, Е. Г. Речицкая и другие).

В исследовании Л. И. Тиграновой и И. Л. Никольской выделен необходимый минимум логических знаний и умений, без овладения которыми процесс развития логического мышления протекает медленно. Этот минимум был обозначен как «логическая грамотность». Л. И. Тиграновой показано, что элементы логики, заложенные в содержании учебного материала начальных классов, без специального вычленения и целенаправленного изучения не усваиваются слабослышащими детьми, не используются в процессе обучения, не становятся инструментом их мышления. Все это обусловливает необходимость пропедевтической работы по формированию приемов логического мышления у детей.

В общепедагогической литературе представлен опыт использования в целях ранней логической и математической пропедевтики (старший дошкольный возраст) логических игр (А. А. Столяр, М. Фидлер), в которых успешно используется дидактический материал «логические блоки» З. Дьенеша (плоский вариант – фигуры), обручи и т. п. Комплект блоков, включенный в математический ящик, состоит из 48 деревянных объемных фигур четырех форм – круглой, треугольной, квадратной, прямоугольной; трех цветов – красного, синего, желтого; двух размеров – большого и маленького; двух видов толщины – толстой и тонкой. Каждый блок характеризуется четырьмя признаками: одной из четырех форм, одним из трех цветов, одним из двух размеров, одним из двух видов толщины. В полном комплекте оказываются исчерпанными все возможные комбинации этих признаков.