Ten different numbers (not necessarily integers) are written down. Any number that is equal to the product of the other nine numbers is then underlined.

At most, how many numbers can be underlined?

[SOLUTION]

105. Placing draughts

Barbara wants to place draughts on a board in such a way that the number of draughts in each row is equal to the number shown at the end of the row, and the number of draughts in each column is equal to the number shown at the bottom of the column. No more than one draught is to be placed in any cell.

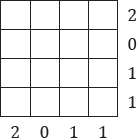
In how many ways can this be done?

[SOLUTION]

Week 16

106. Square roots

How many of the numbers

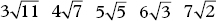
are greater than 10?

[SOLUTION]

107. How many lines?

The picture shows seven points and the connections between them.

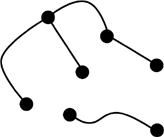
What is the least number of connecting lines that could be added to the picture so that each of the seven points has the same number of connections with other points?

(Connecting lines are allowed to cross each other.)

[SOLUTION]

108. Where in the list?

There are 120 different ways of arranging the letters U, K, M, I and C. All of these arrangements are listed in dictionary order, starting with CIKMU.

Which position in the list does UKIMC occupy?

[SOLUTION]

109. Eva’s sport

Two sportsmen (Ben and Filip) and two sportswomen (Eva and Andrea) − a speed skater, a skier, a hockey player and a snowboarder − had dinner at a square table, with one person on each edge of the square.

The skier sat at Andrea’s left hand.

The speed skater sat opposite Ben.

Eva and Filip sat next to each other.

A woman sat at the hockey player’s left hand.

Which sport did Eva do?

[SOLUTION]

110. Pedro’s numbers

Pedro writes down a list of six different positive integers, the largest of which is N. There is exactly one pair of these numbers for which the smaller number does not divide the larger.

What is the smallest possible value of N?

[SOLUTION]

111. The speed of the train

A train travelling at constant speed takes five seconds to pass completely through a tunnel that is 85 m long, and eight seconds to pass completely through a second tunnel that is 160 m long.

What is the speed of the train?

[SOLUTION]

112. What is ‘pqrst’?

The digits p, q, r, s and t are all different.

What is the smallest five-digit integer ‘pqrst’ that is divisible by 1, 2, 3, 4 and 5?

[SOLUTION]

Crossnumber 4

ACROSS

2. A power of two (4)

5. A prime factor of 12345 (3)

6. Six more than a multiple of 13 ACROSS (3)

8. A cube (2)

10. The product of the digits of 25 ACROSS and also less than half of 23 ACROSS (2)

11. The mean of 4 DOWN, 8 ACROSS, 10 ACROSS, 13 ACROSS and 20 ACROSS and more than 3 DOWN (2)

13. A Fibonacci number (2)

14. A multiple of seven (3)

17. Eight less than a square (3)

19. Seven less than 26 DOWN (2)

20. A number that is greater than 3 DOWN and less than 27 DOWN (2)

22. An even number that is the sum of a square and a triangular number in two different ways (2)

23. A prime whose digits add up to five (2)

25. A square and a multiple of five (3)

28. A multiple of 14 that includes a two and an eight among its digits (3)

29. Nine more than a power of 20 ACROSS (4)

DOWN

1. One hundred and ninety-five less than a square (4)

2. One less than a Fibonacci number (3)

3. The highest common factor of 9 DOWN and 15 DOWN (2)

4. The sum of two powers of two (2)

6. (25 ACROSS) per cent of 24 DOWN (3)

7. The shortest side of a right-angled triangle whose longer sides are 24 DOWN and 25 ACROSS (3)

9. The square of a triangular number; also one less than a multiple of five (3)

12. A factor of 732, each of whose digits is a power of two (3)

15. Five multiplied by 3 DOWN (3)

16. An even square; also a multiple of 8 ACROSS (3)

17. A multiple of 17, the product of whose digits is a square multiplied by seven (3)

18. A multiple of nine (3)

21. A power of 21 (4)

24. A factor of 360 (3)

26. Seven more than 19 ACROSS (2)

27. A cube (2)

[SOLUTION]

Week 17

113. How many routes?

How many different routes are there from S to T that do not go through either of the points U and V more than once?

[SOLUTION]

114. What Rachel drinks

A bottle contains 750 ml of mineral water. Rachel drinks 50% more than Ross, and these two friends finish the bottle between them.

How much does Rachel drink?

[SOLUTION]

115. A magic product square

Place the numbers

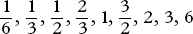
in the squares of the grid, with one number in each square, so that the products of the numbers in the three rows, the three columns and the two diagonals are all equal to 1.

[SOLUTION]

116. What is the angle?

The diagram shows a regular hexagon PQRSTU, a square PUWX and an equilateral triangle UVW.

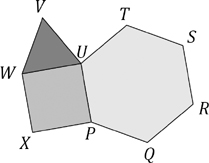
What is the size of angle TVU?

[SOLUTION]

117. A sum of numbers

Consider the list of all four-digit numbers that can be formed using only the digits 1, 2, 3 and 4, with no repetitions.

What is the sum of all the numbers in this list?

[SOLUTION]

118. How many knights?

A group of 25 people consists of knights, serfs and damsels.

Each knight always tells the truth, each serf always lies, and each damsel alternates between telling the truth and lying.

When each of them was asked: ‘Are you a knight?’, 17 of them said ‘Yes’. When each of them was then asked: ‘Are you a damsel?’, 12 of them said ‘Yes’. When each of them was then asked: ‘Are you a serf?’, 8 of them said ‘Yes’.

How many knights are in the group?

[SOLUTION]

119. Crossing the river

Two adults and two children wish to cross a river. They make a raft, but it will carry only the weight of one adult or two children.

What is the minimum number of times the raft must cross the river to get all four people to the other side?

(Note: The raft may not cross the river without at least one person on board.)

[SOLUTION]

Week 18

120. Gluing cubes

A cube is made by gluing together a number of unit cubes face-to-face. The number of unit cubes that are glued to exactly four other unit cubes is 96.

How many unit cubes are glued to exactly five other unit cubes?

[SOLUTION]

121. Mr Gallop’s ponies

Mr Gallop has two stables that each initially housed three ponies. His prize pony, Rein Beau, is worth £250 000. Rein Beau usually spends his day in the small stable, but when he wandered across into the large stable, Mr Gallop was surprised to find that the average value of the ponies in each stable rose by £10 000.

What is the total value of all six ponies?

[SOLUTION]

122. Making a square

I have two types of square tile. One type has a side length of 1 cm and the other has a side length of 2 cm.

What is the smallest square that can be made with equal numbers of each type of tile?

[SOLUTION]

123. How many pairs?

How many pairs of digits (p, q) are there so that the five-digit integer ‘p869q’ is a multiple of 15?

[SOLUTION]

124. What is the product?

Lucy wants to put the numbers 2, 3, 4, 5, 6 and 10 into the circles so that the products of the three numbers along each edge are the same, and as large as possible.

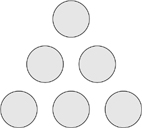
In how many ways can this be done?

[SOLUTION]

125. A five-team league

Five teams played in a competition and every team played once against each of the other four teams. Each team received three points for a match it won, one point for a match it drew and no points for a match it lost.

At the end of the competition the points were as follows:

Yellows 10 Reds 9 Greens 4 Blues 3 Pinks 1

How many of the matches resulted in a draw?

What were the results of the Greens’ matches against the other teams?

[SOLUTION]

126. A mini crossnumber

The solution to each clue of this crossnumber is a two-digit number, not beginning with zero.

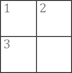
Across

1. A triangular number

3. A triangular number

Down

1. A square

2. A multiple of 5

In how many different ways can the crossnumber be completed correctly?

[SOLUTION]

Shuttle Challenge 2

See Shuttle Challenge 1 for how the Shuttle works.

Question 1

What is the value of

Question 2

[A is the answer to Question 1.]

The number A is an example of a palindromic integer – one that is unchanged when the order of its digits is reversed.

How many palindromic integers are there from 300 to A inclusive?

Question 3

[A is the answer to Question 2.]

The diagram shows a triangle drawn on a square grid made up of nine smaller squares.

The area of the shaded triangle is A cm2.

What is the area, in cm2, of one of the smaller squares?

Question 4

[A is the answer to Question 3.]

Write the number A as a word in the gap shown in the following sentence.

Out of the first __________ letters in this sentence, what fraction is vowels?

Now answer the question.

[SOLUTION]

Week 19

127. Coins in a frame

The diagram shows 10 identical coins that fit exactly inside a wooden frame. As a result, each coin is prevented from sliding.

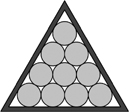
What is the largest number of coins that may be removed so that each remaining coin is still unable to slide?

[SOLUTION]

128. Cheetah v. snail

In a sponsored ‘Animal Streak’, the cheetah ran at 90 kilometres per hour, while the snail slimed along at 20 hours per kilometre. The cheetah kept going for 18 seconds.

Roughly how long would the snail take to cover the same distance as the cheetah?

[SOLUTION]

129. Memorable phone numbers

A new taxi firm needs a memorable phone number. They want a number that has a maximum of two different digits. Their phone number must start with the digit 3 and be six digits long.

How many such numbers are possible?

[SOLUTION]

130. How many games?

Cleo played 40 games of chess and scored 25 points.

A win counts as one point, a draw counts as half a point, and a loss counts as zero points.

How many more games did she win than lose?

[SOLUTION]

131. How many draughts?

Barbara wants to place draughts on a 4 × 4 board in such a way that the number of draughts in each row and in each column are all different. (She may place more than one draught in a square, and a square may be empty.)

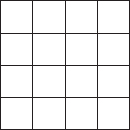
What is the smallest number of draughts that she would need?

[SOLUTION]

132. To and from Jena

In a certain region these are five towns: Freiburg, Göttingen, Hamburg, Ingolstadt and Jena.

One day, 40 trains each made a journey, leaving one of these towns and arriving at another.

10 trains travelled either to or from Freiburg.

10 trains travelled either to or from Göttingen.

10 trains travelled either to or from Hamburg.

10 trains travelled either to or from Ingolstadt.

How many trains travelled either to or from Jena?

[SOLUTION]

133. Largest possible remainder

What is the largest possible remainder that is obtained when a two-digit number is divided by the sum of its digits?

[SOLUTION]

Week 20

134. nth term n

The first term of a sequence of positive integers is 6. The other terms in the sequence follow these rules:

if a term is even then divide it by 2 to obtain the next term;

if a term is odd then multiply it by 5 and subtract 1 to obtain the next term.

For which values of n is the nth term equal to n?

[SOLUTION]

135. How many numbers?

Rafael writes down a five-digit number whose digits are all distinct, and whose first digit is equal to the sum of the other four digits.

How many five-digit numbers with this property are there?

[SOLUTION]

136. A square area

A regular octagon is placed inside a square, as shown.

The shaded square connects the midpoints of four sides of the octagon.

What fraction of the outer square is shaded?

[SOLUTION]

137. ODD plus ODD is EVEN

Find all possible solutions to the ‘word sum’ shown.

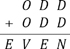
Each letter stands for one of the digits 0−9 and has the same meaning each time it occurs. Different letters stand for different digits. No number starts with a zero.

[SOLUTION]

138. Only odd digits

How many three-digit multiples of 9 consist only of odd digits?

[SOLUTION]

139. How many tests?

Before the last of a series of tests, Sam calculated that a mark of 17 would enable her to average 80 over the series, but that a mark of 92 would raise her average mark over the series to 85.

How many tests were in the series?

[SOLUTION]

140. Three primes

Find all positive integers p such that p, p + 8 and p + 16 are all prime.

[SOLUTION]

Crossnumber 5

ACROSS

1. The cube of a square (5)

4. Eight less than 5 DOWN (3)

6. One less than a multiple of seven (3)

7. A prime factor of 20 902 (4)

10. A number whose digits successively decrease by one (3)

12. Sixty per cent of 20 DOWN (3)

14. A multiple of seven (3)

15. A multiple of three whose digits have an even sum (3)

16. The square of a square (3)

17. A prime that is one less than a multiple of six (3)

19. Eleven more than a cube (4)

22. A number all of whose digits are the same (3)

24. A number that leaves a remainder of eleven when divided by thirteen (3)

25. The square of a prime; the sum of the digits of this square is ten (5)

DOWN

1. A number with an odd number of factors (3)

2. Four less than a triangular number (3)

3. The square root of 9 DOWN (2)

4. A factor of 12 ACROSS (3)

5. The longest side of a right-angled triangle whose shorter sides are 3 DOWN and 4 ACROSS (3)

8. A Fibonacci number (5)

9. The square of 3 DOWN (4)

11. Three more than an even cube (5)

13. A prime factor of 34567 (4)

17. The mean of 10 ACROSS, 16 ACROSS, 18 DOWN, 20 DOWN and 21 DOWN (3)

18. A power of eighteen (3)

20. Two less than 22 ACROSS (3)

21. A number whose digits are those of 12 ACROSS reversed (3)

23. A multiple of twenty-three (2)

[SOLUTION]

Week 21

141. Joey’s and Zoë’s sums

Joey calculated the sum of the largest and smallest two-digit numbers that are multiples of three. Zoë calculated the sum of the largest and smallest two-digit numbers that are not multiples of three.

What is the difference between their answers?

[SOLUTION]

142. When is the party?

Six friends are having dinner together in their local restaurant. The first eats there every day, the second eats there every other day, the third eats there every third day, the fourth eats there every fourth day, the fifth every fifth day and the sixth eats there every sixth day. They agree to have a party the next time they all eat together there. In how many days’ time is the party?

[SOLUTION]

143. A multiple of 11

The eight-digit number ‘1234d678’ is a multiple of 11.

Which digit is d?

[SOLUTION]

144. Two squares

ABCD is a square. P and Q are squares drawn in the triangles ADC and ABC, as shown.

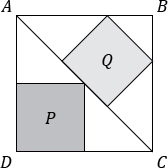
What is the ratio of the area of the square P to the area of the square Q?

[SOLUTION]

145. Proper divisors

Excluding 1 and 24 itself, the positive whole numbers that divide into 24 are 2, 3, 4, 6, 8 and 12. These six numbers are called the proper divisors of 24.

Suppose that you wanted to list in increasing order all those positive integers greater than 1 that are equal to the product of their proper divisors. Which would be the first six numbers in your list?

[SOLUTION]

146. Kangaroo game

In the expression

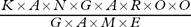
the same letter stands for the same non-zero digit and different letters stand for different digits.

What is the smallest possible positive integer value of the expression?

[SOLUTION]

147. A game with sweets

There are 20 sweets on the table. Two players take turns to eat as many sweets as they choose, but they must eat at least one, and never more than half of what remains. The loser is the player who has no valid move.

Is it possible for one of the two players to force the other to lose? If so, how?

[SOLUTION]

Week 22

148. A 1000-digit number

What is the largest number of digits that can be erased from the 1000-digit number 201820182018 … 2018 so that the sum of the remaining digits is 2018?

[SOLUTION]

149. Gardeners at work

It takes four gardeners four hours to dig four circular flower beds, each of diameter four metres.

How long will it take six gardeners to dig six circular flower beds each of diameter six metres?

[SOLUTION]

150. Overlapping squares

The diagram shows four overlapping squares that have sides of lengths 5 cm, 7 cm, 9 cm and 11 cm.

<1 2 3 4 5 >

На страницу:

Перейти

4 из 5