
Полная версия
The Ultimate Mathematical Challenge: Over 365 puzzles to test your wits and excite your mind

What is the difference between the total area shaded grey and the total hatched area?
[SOLUTION]
151. What can T be?
Each of the numbers from 1 to 10 is to be placed in the circles so that the sum of each line of three numbers is equal to T. Four numbers have already been entered.

Find all the possible values of T.
[SOLUTION]
152. Increases of 75%
Find all the two-digit numbers and three-digit numbers that are increased by 75% when their digits are reversed.
[SOLUTION]
153. Three groups
For which values of the positive integer n is it possible to divide the first 3n positive integers into three groups each of which has the same sum?
[SOLUTION]
154. A board game
Two players, X and Y, play a game on a board that consists of a narrow strip that is one square wide and n squares long. They take turns in placing counters that are one square wide and two squares long on unoccupied squares on the board.

The first player who cannot place a counter on the board loses. X always plays first, and both players always make the best available move.
Who wins the game in the cases where n = 2, 3, 4, 5, 6, 7 and 8?
[SOLUTION]
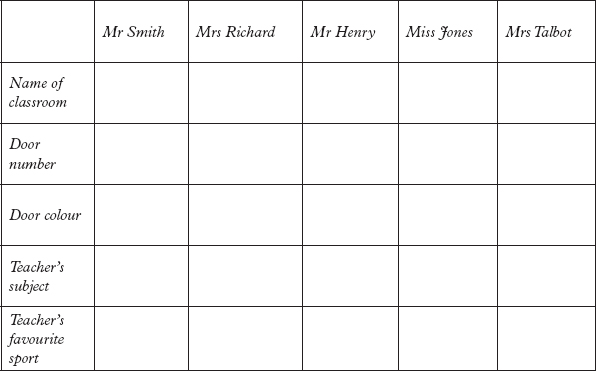
Logic Challenge 3
Five teachers work in a school. By using the clues in the statements below, you need to work out what subject the teacher teaches and what sport they like, and information about their classroom, including the room name and number, and the colour of the classroom door.
Fill in the answer grid with information about each teacher.
Mr Smith teaches Art.
The Science teacher is in the classroom called ‘Square’.
History is taught by Miss Jones.
The favourite sport of Mr Henry does not involve a ball.
Mrs Talbot’s classroom door is coloured yellow and is next to the classroom that has the largest single-digit prime number as its number.
The Maths teacher has the largest classroom door number.
The favourite sport of the teacher in the classroom called ‘Triangle’ is netball.
Miss Jones’s door is coloured orange.
The teacher in the classroom called ‘Circle’ is next to the Maths teacher.
English is taught in the classroom called ‘Sphere’.
The classroom door numbered 3 is next to the teacher who is next to the teacher whose favourite sport is jogging.
Football is the favourite sport of the teacher in the classroom called ‘Cylinder’.
The teacher in the classroom called ‘Square’ is next to the classrooms with the green and orange doors.
The classroom called ‘Cylinder’ is next to the classroom of the Science teacher.
English is taught in the classroom with the ‘unlucky’ prime number.
The classroom door of the Maths teacher is green.
The classroom numbers of Mrs Talbot and Mrs Richard add up to 30.
All the classroom door numbers are prime numbers.
The English teacher is next to a classroom that is next to the classroom of the Science teacher.
The teacher in the classroom with the red door likes rugby and is next to the Maths teacher.
The sum of all the classroom door numbers is 51.
The favourite sport of the teacher in the classroom named ‘Sphere’ is cricket.
The classroom called ‘Triangle’ is next door to the classrooms of the Art and Science teachers.
One of the classrooms has a white door.
[SOLUTION]
Week 23
155. Angles around a triangle

What is the value of a + b + c + d + e + f?
[SOLUTION]
156. Einstein sees two clocks
Albert Einstein was standing on the station platform thinking about relativity when he noticed he could see two station clocks. Each clock was digital, showing only hours and minutes. He observed that the display on one clock changed to the next minute 10 seconds before the correct time, whereas the display on the other clock changed to the next minute 10 seconds after the correct time.
For what fraction of the time did both clocks show the same time?
[SOLUTION]
157. Halving an annulus
The shaded region in the diagram, bounded by two concentric circles, is called an annulus.

The circles have radii 2 cm and 14 cm. The dashed circle divides the area of this annulus into two equal areas.
What is its radius?
[SOLUTION]
158. How many pairs?
How many pairs of numbers (a, b) exist such that the sum a + b, the product ab and the quotient
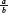
[SOLUTION]
159. Two ages
Abi and Becky were comparing their ages and found that Becky is as old as Abi was when Becky was as old as Abi had been when Becky was half as old as Abi is. The sum of their present ages is 44.
How old is Abi?
[SOLUTION]
160. At McBride Academy
At McBride Academy there are 300 children, each of whom represents the school in both summer and winter sports. In summer, 60% of these play tennis and the other 40% play badminton. In winter, they play hockey or swim, but not both. 56% of the hockey players play tennis in the summer and 30% of the tennis players swim in the winter.
How many both swim and play badminton?
[SOLUTION]
161. Maths, maths, Cayley
How many different solutions are there to this word sum, where each letter stands for a different non-zero digit?

[SOLUTION]
Week 24
162. An angle in a square
The diagram shows a square ABCD and an equilateral triangle ABE.

The point F lies on BC so that EC = EF.
Calculate the angle BEF.
[SOLUTION]
163. Areas in a quarter circle
The diagram shows a quarter circle with centre O and two semicircular arcs with diameters OA and OB.
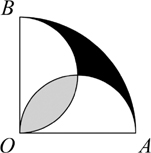
Calculate the ratio of the area of the region shaded grey to the area of the region shaded black.
[SOLUTION]
164. How many extensions?
In a large office, each person has their own telephone extension consisting of three digits, but not all possible extensions are in use. To try to prevent wrong numbers, no used number can be converted to another just by swapping two of its digits.
What is the largest possible number of extensions in use in the office?
[SOLUTION]
165. The top ball
Six pool balls numbered 1 to 6 are to be arranged in a triangle, as shown.

After three balls are placed in the bottom row, each of the remaining balls is placed so that its number is the difference of the two below it.
Which balls can land up at the top of the triangle?
[SOLUTION]
166. Two squares
A square has four digits. When each digit is increased by 1, another square is formed.
What are the two squares?
[SOLUTION]
167. Four vehicles
Four vehicles travelled along a road with constant speeds. The car overtook the scooter at 12:00 noon, then met the bike at 14:00 and the motorcycle at 16:00. The motorcycle met the scooter at 17:00 and overtook the bike at 18:00.
At what time did the bike and the scooter meet?
[SOLUTION]
168. A marching band
A marching band is having difficulty lining up for a parade. When they line up in rows of 3, one person is left over. When they line up in rows of 4, two people are left over. When they line up in rows of 5, three people are left over. When they line up in rows of 6, four people are left over.
However, the band is able to line up in rows of 7 with nobody left over. What is the smallest possible number of marchers in the band?
[SOLUTION]
Crossnumber 6

ACROSS
1. A prime factor of 8765 (4)
4. The interior angle, in degrees, of a regular polygon; its digits have a product of 12 (3)
6. A Fibonacci number whose digits add up to twenty-four (3)
7. A prime that is one greater than a square (2)
8. Ninety-nine greater than the number formed by reversing the order of its digits (3)
10. A multiple of 25 ACROSS (3)
12. 9 DOWN multiplied by seven (3)
15. A number with seven factors (2)
17. The third side of a right-angled triangle with hypotenuse 9 DOWN and other side 25 ACROSS (2)
19. (10 ACROSS) per cent of 8 ACROSS (3)
21. An odd multiple of nine (3)
23. The product of the seventh prime and the eleventh prime (3)
25. An even number (2)
26. The lowest common multiple of 25 ACROSS and 11 DOWN (3)
28. A multiple of eleven, and also the mean of 12 ACROSS, 16 DOWN, 19 ACROSS, 24 DOWN and 27 DOWN (3)
29. A power of nineteen (4)
DOWN
2. An even square (3)
3. One third of 21 ACROSS (2)
4. The interior angle, in degrees, of the regular polygon that has twice as many sides as the regular polygon whose interior angle, in degrees, is 4 ACROSS (3)
5. One less than a multiple of eleven (3)
8. A power of nine (4)
9. The mean of 3 DOWN, 7 ACROSS, 13 DOWN, 17 ACROSS and 27 DOWN (2)
11. Ninety-one less than 10 ACROSS (2)
13. The sum of the squares of the digits of 23 ACROSS (2)
14. A factor of 4567 (4)
16. The difference between 11 DOWN and 3 DOWN (2)
18. The square root of 8 DOWN (2)
20. The highest common factor of 10 ACROSS and 24 DOWN (2)
21. The total number of days in a year in the months whose names do not contain the letter A (3)
22. A prime that is ten less than a cube (3)
24. A square multiplied by five; the product of its digits is 40 (3)
27. A triangular number that is the sum of two prime numbers that differ by eight (2)
[SOLUTION]
Week 25
169. Non-factors of 720
Sam starts to list in ascending order every positive integer that is not a factor of 720.
Which is the tenth number in her list?
[SOLUTION]
170. What size is JMO?
In the diagram, JK and ML are parallel. JK = KO = OJ = OM and LM = LO = LK.

Find the size of the angle JMO.
[SOLUTION]
171. Amrita’s numbers
Amrita has written down four whole numbers. If she chooses three of her numbers at a time and adds up each triple, she obtains totals of 115, 153, 169 and 181.
What is the largest of Amrita’s numbers?
[SOLUTION]
172. Where do the children come from?
Five children, boys Vince, Will and Zac, and girls Xenia and Yvonne, sit at a round table. They come from five different cities: Aberdeen, Belfast, Cardiff, Durham and Edinburgh. The child from Aberdeen sits between Zac and the child from Edinburgh. Neither of the two girls is sitting next to Will. Vince sits between Yvonne and the child from Durham. Zac writes to the child from Cardiff.
Where does each child come from?
[SOLUTION]
173. Find four integers
Find four integers whose sum is 400 and such that the first integer is equal to twice the second integer, three times the third integer and four times the fourth integer.
[SOLUTION]
174. Bradley’s Bicycle Bazaar
In the window of Bradley’s Bicycle Bazaar there are some unicycles, some bicycles and some tricycles. Laura sees that there are seven saddles in total, thirteen wheels in total and more bicycles than tricycles.
How many unicycles are in the window?
[SOLUTION]
175. Liz and Mary’s problems
Liz and Mary compete in solving problems. Each of them is given the same list of 100 problems. For any problem, the first of them to solve it gets 4 points, while the second to solve it gets 1 point. Liz solved 60 problems, and Mary also solved 60 problems. Together, they got 312 points.
How many problems were solved by both of them?
[SOLUTION]
Week 26
176. Edinburgh to London
Travelling by train from Edinburgh to London, I passed a sign saying ‘London 150 miles’. After seven more miles, I passed another sign saying ‘Edinburgh 250 miles’.
How far is it by train from Edinburgh to London?
[SOLUTION]
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.









