All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the nonexclusive, non-transferable right to access and read the text of this e-book on screen. No part of this text may be reproduced, transmitted, downloaded, decompiled, reverse engineered, or stored in or introduced into any information storage retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of HarperCollins e-books.

Find out about HarperCollins and the environment at www.harpercollins.co.uk/green

Source ISBN: 9780008316402

Ebook Edition © November 2018 ISBN: 9780008316419

Version 2018-11-22

Contents

Cover

Title Page

Foreword by Marcus du Sautoy

Introduction

The Problems

Week 1

Week 2

Logic Challenge 1

Week 3

Week 4

Crossnumber 1

Week 5

Week 6

Make a Number Challenge

Week 7

Week 8

Crossnumber 2

Week 9

Week 10

Shuttle Challenge 1

Week 11

Week 12

Crossnumber 3

Week 13

Week 14

Logic Challenge 2

Week 15

Week 16

Crossnumber 4

Week 17

Week 18

Shuttle Challenge 2

Week 19

Week 20

Crossnumber 5

Week 21

Week 22

Logic Challenge 3

Week 23

Week 24

Crossnumber 6

Week 25

Week 26

Shuttle Challenge 3

Week 27

Week 28

Crossnumber 7

Week 29

Week 30

Logic Challenge 4

Week 31

Week 32

Crossnumber 8

Week 33

Week 34

Shuttle Challenge 4

Week 35

Week 36

Crossnumber 9

Week 37

Week 38

Logic Challenge 5

Week 39

Week 40

Crossnumber 10

Week 41

Week 42

Logic Challenge 6

Week 43

Week 44

Crossnumber 11

Week 45

Week 46

Crossnumber 12

Week 47

Week 48

The Penultimate Challenge

Week 49

Week 50

Crossnumber 13

Week 51

Week 52

The Ultimate Challenge

Week 53

Solutions

Problems 1 – 366

Make a Number Challenge

Crossnumbers

Logic Challenges

Shuttle Challenges

The Penultimate Challenge

The Ultimate Challenge

Glossary with Some Useful Facts

Table of Squares, Primes etc.

Acknowledgements

About the Publisher

Foreword

Marcus du Sautoy

There are two things that made me fall in love with mathematics. The first was my teacher at my comprehensive school revealing that there was more to mathematics than long division. Seeing the big stories of mathematics about prime numbers, four-dimensional geometry, symmetry and more made me realise the beauty and creativity that bubbles throughout the subject.

The second was when my teacher introduced me to the puzzles of Martin Gardner in Scientific American. It was then that I got hooked on the amazing buzz you get when you’ve struggled to crack a challenging puzzle and then suddenly you see a clever way to unlock the enigma. Be warned: cracking puzzles releases a very addictive drug.

In this book you can immerse yourself in the joys of the second reason I fell in love with mathematics. Jam-packed with problems that have formed part of the UKMT competitions over the years, these challenges range from those aimed at students taking their first steps onto the mathematical terrain to problems that are for those scaling some of the peaks of the subject.

Although the questions formed part of various competitions, I think it is important to remember that mathematics is not at its heart a competitive sport. As mathematicians we all work together to advance our understanding of the universe of numbers and geometry. Every theorem that we prove relies on all the theorems and proofs that previous generations have laid down right back to the Ancient Greeks. Of all the sciences, mathematics is perhaps unique in the way we truly stand on the shoulders of giants to see further and deeper into our subject.

So the only competitive aspect of the problems for you as a reader is the fun of competing against yourself. Enjoy the problems you can’t solve so easily. They are ultimately the ones that will give you the biggest buzz when you crack them. What gets me up in the morning to go to my desk to do mathematics is all the problems I can’t solve. And when you’ve mastered all the challenges of this book, just remember that mathematics has a whole host of big stories that are still waiting for someone to write the final chapter and reveal the mysteries that still obsess us as mathematicians.

Marcus du Sautoy is Professor of Mathematics and Simonyi Professor for the Public Understanding of Science at the University of Oxford.

Introduction

This book contains a selection of problems drawn from the various competitions and other activities organised by the United Kingdom Mathematics Trust (UKMT).

The UKMT was founded in 1996 by bringing together a number of mathematics competitions for school students organised by three different bodies: the British Mathematical Olympiad Committee, the National Committee for Mathematics Contests and the United Kingdom Mathematics Foundation. Today the UKMT organises a range of different competitions and other activities for students of all ages from 10 to 18, with the stated aim ‘to advance the education of children and young people in mathematics’.

This book consists of one short problem for each day of the year, with an interlude every fourteen days that consists of a longer challenge. The difficulty of the problems varies. We have listed at the end of the book the source of each problem. Together with the description of the competition from which it is drawn, this should give the reader some indication of its intended difficulty. The difficulty of a problem is hard to assess and will naturally depend on the reader. Our intention is that the problems should get gradually harder as each week progresses, and from the start of the year to the end. However, you will probably find many exceptions to this general rule.

Many of the problems were originally set as multiple-choice questions but have been rewritten to remove this feature. This may make some of the problems harder than they originally were, although it should be remembered that in all our competitions students are given only a limited amount of time. It is this time pressure, from which the reader of this book is free, that makes our competitions a tough challenge for school students.

In the Olympiad papers students are asked to write out full solutions and not just give the answer. In marking these papers most of the credit is given for coming up with a cogent and clearly expressed argument; a correct numerical answer by itself counts for little. This feature is missing in the Olympiad problems given in this book, as we are not able to mark your answers! For this reason the full flavour of these problems as presented here is missing. You will find it in the UKMT publications, listed below, which cover the Olympiad problems.

You should also note that the UKMT has a ‘no calculators’ rule for all its competitions. This is because our aim is to encourage good mathematical thinking. Calculators are helpful when numerical answers are required, but using them is often a substitute for thinking. You, dear reader, are, of course, free to use calculators and other electronic devices in tackling these problems, but we think they will only rarely be of any help.

How the problems have been chosen

UKMT problems are designed for students who are currently studying mathematics. In selecting problems for this book aimed at a general reader we have mainly avoided problems that require up-to-date knowledge of the current mathematics curricula. For example, although algebra will often be useful in tackling a problem, we have selected very few problems that are explicitly about algebra. We have included some geometry problems, because geometry is such a beautiful subject. However, most of the problems can be solved using no more than a little numerical knowledge, logical thinking and native wit.

For those whose knowledge is a little rusty we have included a Glossary containing some reminders of mathematical terminology and some basic geometrical facts about angles.

Solutions

To include full solutions, with detailed explanations, to all the problems would require a book four times as large as the current volume. We have therefore generally only given short solutions, but we hope that these will let you know whether you solved the problem correctly, and will be of help if you are ever baffled.

Detailed solutions to many of the problems may be found in the UKMT publications listed below. Solutions to many of the problems, especially those from recent years, may also be downloaded (for free!) from the UKMT website: www.ukmt.org.uk

The range of UKMT competitions

We list below the different UKMT competitions from which these problems have been drawn, giving an indication of the students they are aimed at and the amount of time they are given. Which competition a student is qualified for depends on their school year. Because school years are denominated differently in different parts of the UK, for simplicity we have translated them into the standard ages of the students in these school years.

Primary Team Maths Resources (PTMR)

These are a range of different team activities designed for 10- and 11-year-old students with the aim of facilitating secondary schools in running events for their feeder schools. The activities are mostly similar to those in the Team Maths Challenge but also include some logic problems that we have used for some of our interludes.

Junior Mathematical Challenge (JMC)

Intermediate Mathematical Challenge (IMC)

Senior Mathematical Challenge (SMC)

Each of these papers is made up of 25 multiple-choice questions. The JMC is aimed at students aged 12 or 13, the IMC at students aged 14, 15 or 16, and the SMC at students aged 17 or 18. These papers are often taken by students younger than the target range. For the JMC and IMC, students are given 60 minutes, and for the SMC they are given 90 minutes.

Kangaroo Competitions

The International Mathematical Kangaroo (Kangourou sans Frontières) is an international competition founded in France in 1991 in which over 50 countries now take part. The idea came from the Australian Mathematics Competition, and was named the Kangaroo in recognition of this. The UKMT uses Kangaroo questions for four competitions that are open to students who do sufficiently well in the Challenges, as follows:

Junior Kangaroo for students aged 12 or 13;

Grey Kangaroo for students aged 14;

Pink Kangaroo for students aged 15 or 16;

Senior Kangaroo for students aged 17 or 18.

Each paper consists of 25 questions, for which 60 minutes are allowed. The Junior, Grey and Pink Kangaroo papers are made up of multiple-choice questions. In the Senior Kangaroo, students are asked to give numerical answers but explanations are not required.

Olympiad Papers

These papers are designed for students who do extremely well in the Mathematical Challenges. The heart of all these papers is a small number of tough questions for which fully explained answers are required. They are given the name Olympiad because they are part of a pathway that leads to the UKMT team for the annual International Mathematical Olympiad, a competition in which over one hundred countries take part.

The Olympiad paper that follows on from the Junior Mathematical Challenge is the Junior Mathematical Olympiad for students aged 12 or 13. This is a two-hour paper made up of 10 A-section questions (answers only) and 5 B-section questions (full explanations required).

There are three Olympiad papers that follow on from the Intermediate Mathematical Challenge. These are the Cayley Mathematical Olympiad for students aged 14, the Hamilton Mathematical Olympiad for students aged 15, and the Maclaurin Mathematical Olympiad for students aged 16. Each of these is a two-hour paper with six questions for which full explanations are required. (Before 2004 these papers had A and B sections.)

The Mathematical Olympiad for Girls (MOG) is for girls aged 16 or 17. It aims to encourage and inspire as many girls as possible to get involved in advanced mathematical problem solving. The paper lasts two and a half hours, and consists of five challenging mathematical problems for which full written solutions are required.

There are two British Mathematical Olympiad (BMO) papers – Round 1 and Round 2 – that follow on from the Senior Mathematical Challenge aimed at students aged 17 and 18. To qualify for Round 2, you have to do well in Round 1. The Round 2 questions are therefore very challenging. Students are given three and a half hours for these papers.

The Team Maths Challenge is an event for teams of four students aged 14 or younger. There are over 60 Regional Finals each year, leading to a National Final in June. There are four rounds: the Group Round, the Crossnumber, the Shuttle and the Relay. We have used many of the Crossnumbers for our interludes, where we explain how they work. Questions from other rounds have been used as some of our daily questions. The Senior Team Maths Challenge, which is organised in partnership with the Advanced Mathematics Support Programme, is very similar but aimed at students aged 17 and 18.

We have also included a few problems taken from the UKMT’s Mentoring Scheme. In the scheme students are given monthly problem sheets. They tackle these in their own time, with a mentor who can give them help and who comments on the solutions that are submitted. There is no element of competition.

UKMT publications

We list here the UKMT publications that cover the competitions described above. They contain full solutions to the problems and may be ordered from the UKMT website: www.ukmt.org.uk

Yearbooks

The UKMT has published a Year Book for every year from 1998–99 to 2016–17. Each Year Book includes the problems and solutions for that year’s competitions.

Mathematical Challenges

The following books contain all the papers for the Junior, Intermediate and Senior Mathematical Challenges for the years in question, together with short solutions:

Ten Years of Mathematical Challenges: 1997 to 2006, UKMT, 2006,

Ten Further Years of Mathematical Challenges: 2006 to 2016, UKMT, 2016.

Each of the next three books contains all the problems from the relevant Mathematical Challenge up to the date of publication, arranged by topic and difficulty. The problems are not in multiple-choice format, and the books include hints but not full solutions.

Junior Problems, Andrew Jobbings, UKMT, 2017

Intermediate Problems, Andrew Jobbings, UKMT, 2016

Senior Problems, Andrew Jobbings, UKMT, 2018

In addition, both short and extended solutions for all the Challenge papers for recent years, which include questions for further investigations, may be downloaded for free from the UKMT website.

Mathematical Olympiad

The following books give advice about tackling harder problems at different levels, and include the problems and solutions from different Olympiad competitions, as specified.

First Steps for Problem Solvers, Mary Teresa Fyfe and Andrew Jobbings, UKMT, 2015 – includes all the problems, with solutions, from the Junior Mathematical Olympiad papers from 1999 to 2015.

A Problem Solver’s Handbook, Andrew Jobbings, UKMT, 2013 – includes all the problems, with solutions, from the Intermediate Mathematical Olympiad papers from 2003 to 2012.

A Mathematical Olympiad Primer, 2nd edition, Geoff Smith, UKMT, 2011 – includes all the problems, with solutions, from the British Mathematical Olympiad Round 1 papers from 1996 to 2010.

A Mathematical Olympiad Companion, Geoff Smith, UKMT, 2016 – includes all the problems, with solutions, from the British Mathematical Olympiad Round 2 papers from 2002 to 2016.

The Problems

Week 1

1. How many van loads?

A transport company’s vans each carry a maximum load of 12 tonnes. A firm needs to deliver 24 crates each weighing 5 tonnes.

How many van loads will be needed to do this?

[SOLUTION]

2. An L-ish puzzle

Beatrix places copies of the L-shape shown on a 4 × 4 board so that each L-shape covers exactly three cells of the board.

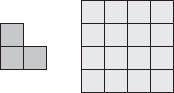
She is allowed to turn around or turn over an L-shape.

What is the largest number of L-shapes she can place on the board without overlaps?

[SOLUTION]

3. Granny’s meter

Yesterday, the reading on Granny’s electricity meter was 098657. She was shocked to realise that all six of these digits are different.

How many more units of electricity will she use before the next time all the digits are different?

[SOLUTION]

4. Paper folding

Three shapes X, Y and Z are shown below.

A sheet of A4 paper (measuring 297 mm × 210 mm) is folded once and placed flat on the table.

Which of these shapes could be made?

[SOLUTION]

5. How many triangles?

In total, how many triangles of any size are there in the diagram?

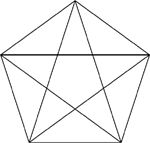
[SOLUTION]

6. Four dice

Rory uses four identical standard dice to build the solid shown in the diagram.

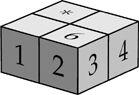
Whenever two dice touch, the numbers on the touching faces are the same. The numbers on some of the faces of the solid are shown.

What number is written on the face marked with an asterisk?

(On a standard dice, the numbers on opposite faces add to 7.)

[SOLUTION]

7. Making 73

Taran thought of a whole number and then multiplied it by either 5 or 6. Krishna added 5 or 6 to Taran’s answer. Finally Eshan subtracted either 5 or 6 from Krishna’s answer.

The final result was 73. What number did Taran choose?

[SOLUTION]

Week 2

8. Decimal time

In the late eighteenth century, a decimal clock was proposed in which there were 100 minutes in each hour and 10 hours in each day.

Assuming that such a clock started at 0.00 at midnight, what time would it show when an ordinary clock showed 6 o’clock the following morning?

[SOLUTION]

9. One size fits all

Harry’s mathematical grandmother keeps a large bag of ‘one size fits all’ socks in a dark cupboard. There are socks in red, blue, pink and green.

How many socks must she pull out to be sure of having a matching pair?

[SOLUTION]

10. Cut the net

The diagram represents a rectangular fishing net made from ropes knotted together at the points shown.

The net is cut several times; each cut severs precisely one section of rope between two adjacent knots.

What is the largest number of such cuts that can be made without splitting the net into two separate pieces?

[SOLUTION]

11. Times are changing

On a digital clock displaying hours, minutes and seconds, how many times in each 24-hour period do all six digits change simultaneously?

[SOLUTION]

12. Making axes

In the addition sum shown, each letter represents a different non-zero digit.

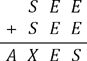
What digit does each letter represent?

[SOLUTION]

1 2 3...5 >

На страницу:

Перейти

1 из 5

Полная версия

The Ultimate Mathematical Challenge: Over 365 puzzles to test your wits and excite your mind

Другие книги автора