
Полная версия
The Ultimate Mathematical Challenge: Over 365 puzzles to test your wits and excite your mind
13. Roundabout
Four cars enter a roundabout at the same time, each one from a different direction, as shown in the diagram.
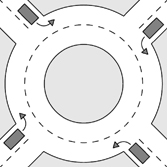
Each car drives in a clockwise direction and leaves the roundabout before making a complete circuit. No two cars leave the roundabout by the same exit.
How many different ways are there for the cars to leave the roundabout?
[SOLUTION]
14. True or false?
None of these statements is true.
Exactly one of these statements is true.
Exactly two of these statements are true.
All of these statements are true.
How many of the statements in the box are true?
[SOLUTION]
Logic Challenge 1
The team photograph
A photograph is to be taken of the school mixed five-a-side football squad, which includes three substitutes. The girls in the squad are Liz, Jenny, Sarah and Tracey. The boys are Alan, Matthew, Peter and Steve.
The team line up in two rows of four. Read the clues below to work out who is standing where and what number they are wearing (which will be one of the numbers from 1 to 8).
Place the number in the top square of the answer grid and the name in the bottom square of each row.
The clues
Tracey is in the front row in front of Jenny.
The average of the two numbers in the middle of the front row is Sarah’s number, a square.
Peter is not sitting next to a girl.
Steve is sitting between Liz and Jenny.
Players with prime numbers, which includes Alan, are sitting in the front row.
There is only one boy on the end of a row.
In both the front and back rows the two places on the right (as you look at it) are filled by a boy and a girl.
Matthew and Steve have the highest and lowest numbers a boy could wear.
Jenny’s number is three times as large as Tracey’s and twice as large as that of Peter, who is not sitting on the end of a row.
Girls have even numbers.
Back row

Front row

[SOLUTION]
Week 3
15. A line of lamp posts
Four lamp posts are in a straight line. The distance from each post to the next is 25 metres.
What is the distance from the first post to the last?
[SOLUTION]
16. Sums of digits
For how many three-digit numbers does the sum of the digits equal 25?
[SOLUTION]
17. A million seconds
How many days, to the nearest day, are there in a million seconds?
[SOLUTION]
18. Sum to 100
The sum of 10 distinct positive integers is 100. What is the largest possible value of any of the 10 integers?
[SOLUTION]
19. x marks the spot
The numbers 2, 3, 4, 5, 6, 7, 8 are to be placed, one per square, in the diagram shown such that the four numbers in the horizontal row add up to 21 and the four numbers in the vertical column also add up to 21.
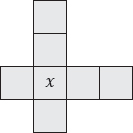
Which number should replace x?
[SOLUTION]
20. The last Wednesday
One of the months in a particular year has five Wednesdays, and the third Saturday is the 19th.
Which day of the month is the last Wednesday?
[SOLUTION]
21. Her brother’s age
A woman says to her brother, ‘I am four times as old as you were when I was the same age as you are now.’
The woman is 40 years old.
How old is her brother now?
[SOLUTION]
Week 4
22. Pings and pongs
Five pings and five pongs are worth the same as two pongs and eleven pings.
How many pings is a pong worth?
[SOLUTION]
23. How many sides?
A single polygon is made by joining dots in the grid with straight lines, which meet only at dots at their end points. No dot is at more than one corner. The diagram shows a five-sided polygon formed in this way.
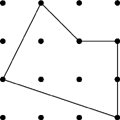
What is the greatest possible number of sides of a polygon formed by joining the dots using these same rules?
[SOLUTION]
24. A tennis club
Three-quarters of the junior members of a tennis club are boys and the rest are girls. What is the ratio of boys to girls among these members?
[SOLUTION]
25. Rectangles in a square
Five equal rectangles are placed inside a square with side length 24 cm, as shown in the diagram.
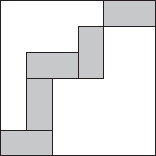
What is the area in cm2 of one rectangle?
[SOLUTION]
26. The absent present
Four children bought a birthday present for their father. One of the children hid the present. When their mother asked them who had hidden the present, the four children made the following statements:
Alfred: ‘It was not me!’
Benjamin: ‘It was not me!’
Christian: ‘It was Daniel!’
Daniel: ‘It was Benjamin!’
It turned out that exactly one of them did not tell the truth.
Who hid the present?
[SOLUTION]
27. Professor Brainstorm’s clock
Professor Brainstorm’s clock gains 16 minutes every day.
After she has set it to the correct time, how many days pass before it next tells the correct time?
[SOLUTION]
28. What is n?
You are given that n is a positive integer with the property that when we add n and the sum of its digits, we obtain the number 313.
What are the possible values of n?
[SOLUTION]
Crossnumber 1
A crossnumber works just like a crossword except that, instead of filling each square with one of the letters from A to Z, you have to fill each square with a single digit from 0 to 9.

ACROSS
1. The square of an odd number (2)
3. 18 DOWN divided by six (3)
6. A number divisible by three (3)
7. A factor of 14 ACROSS (3)
9. An odd number that is one more than a cube (2)
10. One more than a number divisible by nine (2)
12. A number divisible by both six and a square greater than one (3)
14. A multiple of 7 ACROSS (3)
16. The sum of twice 1 ACROSS and 14 (2)
18. Seven less than a square (2)
19. One more than three times 6 ACROSS (3)
21. A Fibonacci number divisible by seven (3)
22. A palindrome that is twice a prime (3)
23. (9 ACROSS × 4) − 13 DOWN (2)
DOWN
2. A palindrome (3)
3. (3 × 9 ACROSS) − (1 ACROSS + 23 ACROSS) (3)
4. The product of two primes (2)
5. One less than a perfect number (2)
8. A cube that is also a power of two (3)
9. A factor of 6111 (3)
11. The sum of the digits of 8 DOWN and 21 ACROSS (2)
12. A number divisible by four (2)
13. A prime that is also a Fibonacci number (3)
15. Three times a prime and six greater than a square (3)
17. One less than a multiple of nine (3)
18. A number divisible by three (3)
19. (12 DOWN × 2) − 5 (2)
20. The sum of the digits of 14 ACROSS is one more than twice the sum of the digits of this number (2)
[SOLUTION]
Week 5
29. Turbo the tortoise
Usain runs twice as fast as his mum. His mum runs five times as fast as his pet tortoise, Turbo. They all set off together for a run down the same straight path.
When Usain has run 100 metres, how far apart are his mum and Turbo the tortoise?
[SOLUTION]
30. Rolling a cube
A cube is being rolled on a plane so it turns around its edges. Its bottom face passes through the positions 1, 2, 3, 4, 5, 6 and 7 in that order, as shown.

Which of these two positions were occupied by the same face of the cube?
[SOLUTION]
31. Small change
My bus fare is 44p. If the driver can give me change, what is the smallest number of coins that must change hands when I pay this fare?
[The coins available are 1p, 2p, 5p, 10p, 20p, 50p, £1 and £2.]
[SOLUTION]
32. Eight factors
The number 78 has exactly eight factors, including 1 and 78.
Which is the smallest integer greater than 78 that has eight factors?
[SOLUTION]
33. A small sum
In the addition sum ‘TAP’ + ‘BAT’ + ‘MAN’, each letter must represent a different digit and no first digit is zero.
What is the smallest sum that can be obtained?
[SOLUTION]
34. A circle on a grid
A circle is added to the grid shown.

What is the largest number of dots that the circle can pass through?
[SOLUTION]
35. Numbers around a circle
Five integers are written around a circle in such a way that no two or three consecutive numbers have a sum that is a multiple of 3. Of the five numbers, how many are themselves multiples of 3?
[SOLUTION]
Week 6
36. Digit sum 2001
Which is the smallest positive integer whose digits add up to 2001?
[SOLUTION]
37. Seven semicircular arcs
The diagram shows a curve made from seven semicircular arcs, the radius of each of which is 1 cm, 2 cm, 4 cm or 8 cm.
What is the length of the curve?
[SOLUTION]
38. Sorting dominoes
Dominoes are said to be arranged correctly if, for each pair of adjacent dominoes, the numbers of spots on the adjacent ends are equal. Paul laid six dominoes in a line, as shown in the diagram.

He can make a move either by swapping the position of any two dominoes (without rotating either domino) or by rotating one domino.
What is the smallest number of moves he needs to make to arrange all the dominoes correctly?
[SOLUTION]
39. Mr Ross
Mr Ross always tells the truth on Thursdays and Fridays but always tells lies on Tuesdays. On the other days of the week he tells the truth or tells lies, at random. For seven consecutive days he was asked what his first name was, and on the first six days he gave the following answers, in order: John, Bob, John, Bob, Pit, Bob.
What was his answer on the seventh day?
[SOLUTION]
40. Missing number
Ria wants to write a number in each of the seven bounded regions in the diagram.
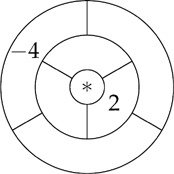
Two regions are neighbours if they share part of their boundary. The number in each region is to be the sum of the numbers in all of its neighbours.
Ria has already written in two of the numbers, as shown.
What number must she write in the central region?
[SOLUTION]
41. How many moves?
A puzzle starts with nine numbers placed in a grid, as shown.
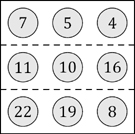
On each move you are allowed to swap any two numbers. The aim is to arrange for the total of the numbers in each row to be a multiple of 3.
What is the smallest number of moves needed?
[SOLUTION]
42. The perimeter of a square
The diagram shows a square that has been divided into five congruent rectangles. The perimeter of each rectangle is 51 cm.

What is the perimeter of the square?
[SOLUTION]
Make a Number Challenge
In each case you are given some numbers and are challenged to use them to make the target number.
You can use the basic mathematical operations + − × ÷ and brackets, but no other mathematical symbols.
You can use each of the given numbers just once, but you don’t have to use all the numbers. You can’t put digits together to make larger numbers and you can’t use exponents.
Example: Use 1, 2, 3 and 8 to make 27.
Answer: (1 + 8) × 3 and 8 × 3 + 1 + 2 are both correct. However, 81 ÷ 3 and 31+2 are not acceptable answers.
The following challenges are taken from the Primary Team Maths Resources for 2015.
Question 1
Use 1, 4, 4, 6, 6 and 75 to make 324.
Question 2
Use 1, 2, 4, 6, 7 and 50 to make 405.
Question 3
Use 1, 2, 3, 3, 6 and 100 to make 154.
Question 4
Use 1, 4, 5, 8, 9 and 75 to make 760.
Question 5
Use 5, 6, 8, 8, 9 and 25 to make 426.
Question 6
Use 1, 2, 4, 6, 7 and 75 to make 441.
Question 7
Use 1, 2, 3, 5, 7 and 25 to make 851.
Question 8
Use 2, 4, 5, 7, 8 and 25 to make 594.
Question 9
Use 1, 2, 6, 7, 8 and 25 to make 483.
Question 10
Use 1, 5, 6, 6, 7 and 100 to make 521.
[SOLUTION]
Week 7
43. Easter eggs
Mary has three brothers and four sisters.
If they, and Mary, all buy each other an Easter egg, how many eggs will be bought?
[SOLUTION]
44. A shape sum
In the sum shown, different shapes represent different digits.
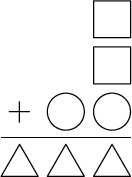
What digit does the square represent?
[SOLUTION]
45. The pages of a newspaper
A newspaper has thirty-six pages.
Which other pages are on the same sheet as page 10?
[SOLUTION]
46. The sum of two primes
The number 12 345 can be expressed as the sum of two primes in exactly one way.
What is the larger of the two primes?
[SOLUTION]
47. A perimeter
The diagram shows three touching circles, each of radius 5 cm, and a line touching two of them.
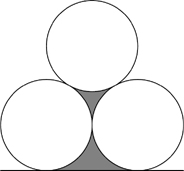
What is the total length of the perimeter of the shaded region?
[SOLUTION]
48. The oldest tree
Today the combined age of three oak trees is exactly 900 years. When the youngest tree has reached the present age of the middle tree, the middle tree will be the present age of the oldest tree and four times the present age of the youngest tree.
What is the present age of the oldest tree?
[SOLUTION]
49. Who’s done their homework?
Miss Spelling, the English teacher, asked five of her students how many of the five of them had done their homework the day before. Daniel said none, Ellen said only one, Cara said exactly two, Zain said exactly three and Marcus said exactly four. Miss Spelling knew that the students who had not done their homework were not telling the truth but those who had done their homework were telling the truth.
How many of these students had done their homework the day before?
[SOLUTION]
Week 8
50. A stack of cubes
Katie writes a different positive integer on the top face of each of the fourteen cubes in the pyramid shown.
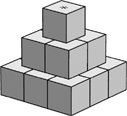
The sum of the nine integers written on the cubes in the bottom layer is 50. The integer written on each of the cubes in the middle and top layers of the pyramid is equal to the sum of the integers on the four cubes underneath it.
What is the greatest possible integer that she can write on the top cube?
[SOLUTION]
51. The largest remainder
Gregor divides 2015 successively by 1, 2, 3, and so on up to and including 1000. He writes down the remainder for each division.
What is the largest remainder he writes down?
[SOLUTION]
52. Go on and on and on and on
In this addition, G, N and O represent different digits, none of which is zero.

What are the numbers in this sum?
[SOLUTION]
53. A list of primes
Alice writes down a list of prime numbers less than 100, using each of the digits 1, 2, 3, 4 and 5 only once and using no other digits.
Which prime number must be in her list?
[SOLUTION]
54. Continue the pattern
The diagram shows the first three patterns in a sequence in which each pattern has a square hole in the middle.

How many small shaded squares are needed to build the tenth pattern in the sequence?
[SOLUTION]
55. How many codes?
Peter has a lock with a three-digit code. He knows that all the digits of his code are different, and that if he divides the second digit by the third and then squares his answer he will get the first digit.
What is the difference between the largest and smallest possible codes?
[SOLUTION]
56. A word product
What is the value of P + Q + R in the multiplication shown?
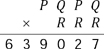
[SOLUTION]
Crossnumber 2

ACROSS
1. The highest common factor of 5 DOWN and 8 DOWN (2)
3. A prime factor of 2007 (3)
5. 3 DOWN plus the square root of 4 DOWN (3)
6. The product of three consecutive integers, two of which are prime (3)
7. One less than a multiple of 2 DOWN (3)
9. Five less than 14 ACROSS (4)
11. Seven more than the product of the digits of 22 ACROSS (2)
13. Three more than a triangular number (2)
14. 9 ACROSS plus five (4)
16. A square whose digit sum is three more than its square root (3)
18. Three times the product of two consecutive prime numbers (3)
21. The mean of 11 ACROSS and 21 ACROSS is 16 ACROSS (3)
22. Twice a prime number (3)
23. Two less than a square (2)
DOWN
1. Eight less than a multiple of nine (3)
2. A prime factor of 12 DOWN (2)
3. A Fibonacci number that is also a prime (3)
4. A square (2)
5. One less than twice a triangular number (3)









