
Полная версия
The Ultimate Mathematical Challenge: Over 365 puzzles to test your wits and excite your mind
7. 10 DOWN minus three (4)
8. One third the product of three consecutive numbers, two of which are prime (3)
10. 7 DOWN plus three (4)
12. A number whose digit sum is equal to one of its factors (3)
15. The product of two consecutive prime numbers (3)
17. p4 + 1, where p is prime (3)
19. The sum of 16 ACROSS and 3 ACROSS (3)
20. Six less than twice 13 ACROSS (2)
21. Fifteen plus the mean of 1 ACROSS and 11 ACROSS (2)
[SOLUTION]
Week 9
57. Three Tuesdays
Three Tuesdays of a month fall on even-numbered dates.
Which day of the week was the twenty-first day of the month?
[SOLUTION]
58. Crack the code
In a seven-digit numerical code, each group of four adjacent digits adds to 16 and each group of five adjacent digits adds to 19.
What is the code?
[SOLUTION]
59. Mr Bean’s fruit
Despite his name, Mr Bean likes to eat lots of fruit. He finds that four apples and two oranges cost £1.54 and that two oranges and four bananas cost £1.70.
How much would he have to pay if he bought one apple, one orange and one banana?
[SOLUTION]
60. Ali’s bookshelves
Ali is arranging the books on his bookshelves. He puts half his books on the bottom shelf and two-thirds of what remains on the second shelf. Finally, he splits the rest of his books over the other two shelves so that the third shelf contains four more books than the top shelf. There are three books on the top shelf.
How many books are on the bottom shelf?
[SOLUTION]
61. An unfair dice
I have an unfair dice that has probability
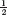
[SOLUTION]
62. A room in Ginkrail
The town of Ginkrail is inhabited entirely by knights and liars. Every sentence spoken by a knight is true, and every sentence spoken by a liar is false. One day some inhabitants of Ginkrail were alone in a room and three of them spoke.
The first one said: ‘There are no more than three of us in the room. All of us are liars.’
The second said: ‘There are no more than four of us in the room. Not all of us are liars.’
The third said: ‘There are five of us in the room. Three of us are liars.’
How many people were in the room and how many liars were among them?
[SOLUTION]
63. Curious integers
In the following puzzle, each different capital letter represents a different digit. Thus ‘SEVEN’ represents a five-digit decimal number.
‘SEVEN’ is prime and, as one would expect, ‘SEVEN’ minus ‘THREE’ equals ‘FOUR’.
Curiously, ‘FOUR’ is prime (as is ‘RUOF’) but ‘THREE’ is not prime. Another oddity is that ‘TEN’ is a square.
Find the values of ‘FOUR’ and ‘TEN’.
[SOLUTION]
Week 10
64. Eight factors
A certain number has exactly eight factors including 1 and itself. Two of its factors are 21 and 35.
What is the number?
[SOLUTION]
65. A nonagon problem
The diagram shows a regular nine-sided polygon (a nonagon or an enneagon) with two of the sides extended to meet at the point X.
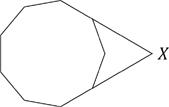
What is the size of the acute angle at X?
[SOLUTION]
66. How many primes?
Peter wrote a list of all the numbers that could be produced by changing one digit of the number 200.
How many of the numbers on Peter’s list are prime?
[SOLUTION]
67. Fill in the blanks
Sam wants to complete the diagram so that each of the nine circles contains one of the digits from 1 to 9 inclusive and each contains a different digit.
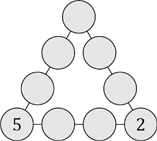
Also, the digits in each of the three lines of four circles must have the same total. What is this total?
[SOLUTION]
68. The school netball league
In our school netball league, a team gains a certain whole number of points if it wins a game, a lower whole number of points if it draws a game and no points if it loses a game.
After 10 games my team has won 7 games, drawn 3 and gained 44 points. My sister’s team has won 5 games, drawn 2 and lost 3.
How many points has her team gained?
[SOLUTION]
69. How many zogs?
The currency used on the planet Zog consists of bank notes of a fixed size differing only in colour. Three green notes and eight blue notes are worth 46 zogs; eight green notes and three blue notes are worth 31 zogs.
How many zogs are two green notes and three blue notes worth?
[SOLUTION]
70. How many V-numbers?
A three-digit integer is called a ‘V-number’ if the digits go ‘high-low-high’ – that is, if the tens digit is smaller than both the hundreds digit and the units (or ‘ones’) digit.
How many three-digit ‘V-numbers’ are there?
[SOLUTION]
Shuttle Challenge 1
In the Shuttle rounds of the Team and Senior Team Maths Challenges, each team of four students is divided into two pairs who sit at opposite ends of a table. One pair tackles questions 1 and 3; the other pair attempts questions 2 and 4. The numerical answer to question 1 is passed across the table to the other pair who need it to answer question 2, and so on. The answer that is passed on is called A in the subsequent question.
The teams have eight minutes to answer all four questions. They get bonus marks if they answer all the questions correctly within six minutes.
How long will it take you?
Question 1
What is the value of (42 + 52) × 72?
Question 2
[A is the answer to Question 1.]
At which number will the minute hand of a clock be pointing to (A + 1) minutes after midnight?
Question 3
[A is the answer to Question 2.]
John has three sticks that he has formed into a triangle. The length of each stick is a whole number of centimetres.
The length of one of the sticks is (A + 1) cm, and the length of another of the sticks is (A − 1) cm.
How many different possibilities are there for the length of John’s third stick?
Question 4
[A is the answer to Question 3.]
A pyramid with a polygonal base has A faces.
How many edges does the pyramid have?
[SOLUTION]
Week 11
71. A magic square
In a magic square, each row, each column and both main diagonals have the same total.
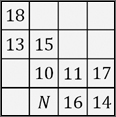
In the partially completed magic square shown, what number should replace N?
[SOLUTION]
72. Fly, fly, fly away
In this addition sum, each letter represents a different non-zero digit.

What are the numbers in this sum?
[SOLUTION]
73. What is the units digit?
Catherine’s computer correctly calculates
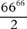
What is the units digit of its answer?
[SOLUTION]
74. Minnie’s training
After a year’s training, Minnie Midriffe increases her average speed in the London Marathon by 25%.
By what percentage did her time decrease?
[SOLUTION]
75. Telling the truth
The Queen of Hearts always lies for the whole day or always tells the truth for the whole day.
Which of these statements can she never say?
A. ‘Yesterday, I told the truth.’
B. ‘Yesterday, I lied.’
C. ‘Today, I tell the truth.’
D. ‘Today, I lie.’
E. ‘Tomorrow, I shall tell the truth.’
[SOLUTION]
76. What is the unshaded area?
Eight congruent semicircles are drawn inside a square of side length 4.

Each semicircle begins at a vertex of the square and ends at a midpoint of an edge of the square.
What is the area of the unshaded part of the square?
[SOLUTION]
77. Aimee goes to work
Every day, Aimee goes up an escalator on her journey to work. If she stands still, it takes her 60 seconds to travel from the bottom to the top. One day the escalator was broken so she had to walk up it. This took her 90 seconds.
How many seconds would it take her to travel up the escalator if she walked up at the same speed as before while it was working?
[SOLUTION]
Week 12
78. The pages of a book
The pages of a book are numbered 1, 2, 3, and so on. In total, it takes 852 digits to number all the pages of the book. What is the number of the last page?
[SOLUTION]
79. A letter sum
Each letter in the sum shown represents a different digit.
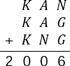
The letter A represents an odd digit.
What are the numbers in this sum?
[SOLUTION]
80. Timi’s ears
Three inhabitants of the planet Zog met in a crater and counted each other’s ears. Imi said, ‘I can see exactly 8 ears’; Dimi said, ‘I can see exactly 7 ears’; Timi said, ‘I can see exactly 5 ears.’ None of them could see their own ears.
How many ears does Timi have?
[SOLUTION]
81. Unusual noughts and crosses
In this unusual game of noughts and crosses, the first player to form a line of three Os or three Xs loses.
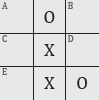
It is X’s turn. Where should she place her cross to make sure that she does not lose?
[SOLUTION]
82. An average
The average of 16 different positive integers is 16.
What is the greatest possible value that any of these integers could have?
[SOLUTION]
83. Painting a cube
Each face of a cube is painted with a different colour from a selection of six colours.
How many different-looking cubes can be made in this way?
[SOLUTION]
84. A Suko puzzle
In the puzzle Suko, the numbers from 1 to 9 are to be placed in the spaces (one number in each) so that the number in each circle is equal to the sum of the numbers in the four surrounding spaces.
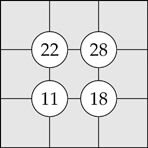
How many solutions are there to the Suko puzzle shown?
[SOLUTION]
Crossnumber 3

ACROSS
2. The sum of a square and a cube (3)
4. Nine less than half 26 ACROSS (2)
6. 13 DOWN plus 5 DOWN minus 2 ACROSS minus 10 DOWN (3)
7. A prime factor of (6 ACROSS plus 15) (2)
8. The square root of 4 ACROSS cubed (2)
9. One more than a multiple of 8 (3)
12. Fifteen less than a cube (2)
14. A multiple of fourteen (3)
17. A prime greater than 13 and whose digits are different (2)
18. The mean of 5 DOWN, 21 DOWN and 28 ACROSS (2)
19. Three more than a square (3)
22. An even number that is less than 24 DOWN (2)
24. The sum of 9 ACROSS and a multiple of five (3)
26. The difference of two two-digit triangular numbers and also one more than an odd square (2)
28. The first two digits of the square of 17 ACROSS (2)
29. The hypotenuse of a triangle whose shorter sides are 21 DOWN and 20 DOWN (3)
30. The lowest common multiple of 10 DOWN and 15 DOWN (2)
31. A factor of 6789 (3)
DOWN
1. The square of (one more than a multiple of 29) (4)
2. A prime factor of 2008 (3)
3. A Fibonacci number that is one more than 2 ACROSS (3)
5. Two less than 11 DOWN minus 4 ACROSS (2)
10. Eight more than half 4 ACROSS (2)
11. The sum of a Fibonacci number and a triangular number in three distinct ways (2)
13. The number whose digits are those of 31 ACROSS reversed (3)
14. 3 DOWN plus 11 DOWN (3)
15. A multiple of 5 that is less than 16 DOWN (2)
16. A power of 2 that is greater than 4 ACROSS and less than 28 ACROSS (2)
20. The exterior angle, in degrees, of a regular polygon (2)
21. 70 per cent of 30 ACROSS (2)
23. A prime whose digits are increasing consecutive numbers (4)
24. A power of 2 multiplied by a power of 3 (3)
25. Three less than a multiple of seven (3)
27. 11 DOWN plus 15 plus a quarter of 4 ACROSS (2)
[SOLUTION]
Week 13
85. The Beans’ beans
The Bean family are very particular about beans. At every meal all Beans eat some beans. Pa Bean always eats more beans than Ma Bean but never eats more than half the beans. Ma Bean always eats the same number of beans as both of their children together and the two children always eat the same number of beans as each other. At their last meal they ate 23 beans.
How many beans did Pa Bean eat?
[SOLUTION]
86. Palindromic years
The number 2002 is a palindrome, since it reads the same forwards and backwards.
For how many other years this century will the number of the year be a palindrome?
[SOLUTION]
87. Swallowing spiders
It was reported recently that, in an average lifetime of 70 years, each human is likely to swallow around 8 spiders while sleeping.
Supposing that the population of the UK is around 60 million, what is the best estimate of the number of unfortunate spiders consumed in this way in the UK each year?
[SOLUTION]
88. Multiple missing digits
The two-digit by two-digit multiplication shown has lots of digits missing.

What are the missing digits?
[SOLUTION]
89. Pippa’s visit
Pippa is visiting her grandparents. She spends half the time playing, a third sleeping and the remaining 35 minutes eating.
How long is her visit?
[SOLUTION]
90. Possible ps
The eight-digit number ‘ppppqqqq’, where p and q are digits, is a multiple of 45.
What are the possible values of p?
[SOLUTION]
91. A magic square
A 3 × 3 grid contains nine numbers, not necessarily integers, one in each cell. Each number is doubled to obtain the number on its immediate right and trebled to obtain the number immediately below it.
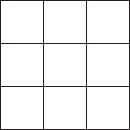
The sum of the nine numbers is 13. What is the number in the central cell?
[SOLUTION]
Week 14
92. A line of coins
Sixty 20p coins are lined up side by side. Every second 20p coin is then replaced by a 10p coin. Then every third coin is replaced by a 5p coin. Finally, every fourth coin in the row is replaced by a 2p coin.
What is the final value of all the coins in the line?
[SOLUTION]
93. What is the area?
The figure shows two shapes that fit together exactly.
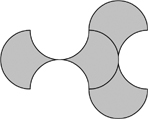
Each shape is formed by four semicircles of radius 1. What is the total shaded area?
[SOLUTION]
94. My children’s ages
The product of my children’s ages is 1664. The youngest is half as old as the eldest.
How many children do I have?
[SOLUTION]
95. Tickets for a school play
Tickets for a school play cost £3 for adults and £1 for children. The total amount collected from ticket sales was £1320. The play was staged in a hall seating 600, but the hall was not completely full.
What was the smallest possible number of adults at the play?
[SOLUTION]
96. A mini crossnumber
The solution to each clue of this crossnumber is a two-digit number. None of these numbers begins with zero.
Complete the crossnumber.
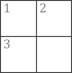
Across
1. Multiple of 3
3. Three times a prime
Down
1. Multiple of 25
2. Square
[SOLUTION]
97. What is ‘abc’?
The letters a, b and c stand for non-zero digits. The integer ‘abc’ is a multiple of 3; the integer ‘cbabc’ is a multiple of 15; and the integer ‘abcba’ is a multiple of 8.
What is the integer ‘abc’?
[SOLUTION]
98. The ninth term
In a sequence of positive integers, each term is larger than the previous term. Also, after the first two terms, each term is the sum of the previous two terms.
The eighth term of the sequence is 390. What is the ninth term?
[SOLUTION]
Logic Challenge 2
Five clowns are standing in a line. They are being judged as to who is the most colourful clown.
Read the clues below to work out where each clown is standing in the line, and what colour hat, hair, nose and shoes they are wearing. Here ‘left’ and ‘right’ refer to the position in which the clowns appear to someone who is standing facing them.
The blue hat is worn by Jessie.
The red hat is worn by the clown with the blue nose.
Amy has green hair.
Jessie is on the left, at the end of the row, wearing yellow shoes.
Mitch, with yellow hair, has Jessie and Amy next to him.
Kenny is immediately to the right of the clown with red shoes.
Alby has red hair.
The middle clown in the line-up facing the class has a yellow nose.
Both Jessie and Kenny are wearing yellow shoes.
The clown with yellow hair is standing in between clowns wearing yellow and red shoes.
A clown with a blue nose is next to a clown wearing a blue hat.
Neither Mitch nor Jessie are wearing anything green.
For each clown except Amy, their hat, hair, nose and shoes are different colours.
Kenny’s hat, Jessie’s hair, Mitch’s shoes and Alby’s nose are all the same colour.
The hats worn by the five clowns are all different colours. The same is also true for their hair and noses.
Alby’s hair is the same colour as Amy’s shoes, and Amy’s hair is the same colour as Alby’s shoes.
Everyone except Amy is wearing something that is orange.
[SOLUTION]
Week 15
99. Folded shapes
A sheet of A4 paper (297 mm × 210 mm) is folded once and then laid flat on the table.
Which of these shapes could not be made?

[SOLUTION]
100. Einstein’s clocks
Albert Einstein is experimenting with two unusual clocks that both have 24-hour displays. One clock goes at twice the normal speed. The other clock goes backwards, but at the normal speed. Both clocks show the correct time at 13:00.
What is the correct time when the displays on the clocks next agree?
[SOLUTION]
101. The total area
The diagram shows three semicircles, each of radius 1.
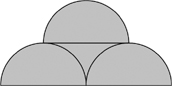
What is the size of the total shaded area?
[SOLUTION]
102. How many weeks?
How many weeks are there in 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 minutes?
[SOLUTION]
103. A platinum question
Platinum is a very rare metal, even rarer than gold. Its density is 21.45 g/cm3. Assuming that the world production has been about 110 tonnes for each of the past 50 years, and negligible before that, which of the following has a comparable volume to that of the total amount of platinum ever produced?









