Некоторые аспекты оценки эффективности функционирования систем. Вторая редакция, исправленная и дополненная

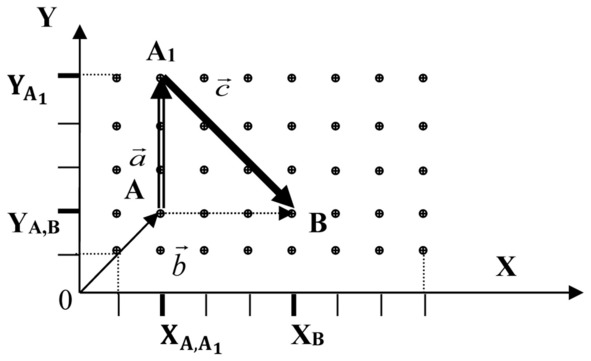
Рисунок 12 Движение с использованием ресурсов с предварительной подготовкой

Сказанное для обычных ресурсозависимых параметров справедливо и для стабилизируемых ресурсозависимых параметров – если объекту необходимо поддерживать стабильное значение параметра в период функционирования и отсутствует возможность постоянной подпитки извне, то необходимо обеспечить запас ресурса, что также приведет формально к соответствующему уводу объекта от цели в начальный период операции.

Сделаем несколько замечаний:

– если объект готов совершать движение со снижением значения параметра ресурса относительно исходного значения, то предварительное увеличение значения ресурса может быть меньшим, нежели может потребоваться в соответствии с прогнозируемыми тратами;

— если объекту необходимо закончить движение в точке цели с повышением ресурса относительно исходного значения, то предварительное увеличение значения параметра ресурса следует сделать больше, нежели может потребоваться в соответствии с прогнозируемыми тратами;

– текущее значение ресурса только определяет состояние объекта, ни коим образом не гарантируя полноценное (то есть абсолютно точное решение поставленных задач) затратное перемещение, так как в процессе движения к цели или ее удержания могут возникнуть дополнительные потребности в ресурсе;

– попытка вернуться в исходное состояние в условиях необходимости использования ресурса требует такой же подготовки, что и обычное перемещение в пространстве состояний;

– использованный ресурс может быть восстановлен за счет подпитки (использования ресурса) извне системы либо действиями самой системы, либо действиями другой системы с помощью информационных векторов (смотри ниже) или генераторов ресурсов. Тогда движение объекта за счет ресурсов не сопровождается отклонением объекта от намеченной цели и не требует предварительной подготовки по дополнительному резервированию ресурсов. При наличии стабилизируемых параметров постоянное поступление ресурсов обеспечивает неотклонение объекта от цели, хотя он при этом и не движется;

– следует отметить, в соответствии с терминологией пространства состояний и приведенным в начале данного параграфа понятием ресурса, ресурсом является только тот параметр, исчерпание которого, т.е. уменьшение значения, требуется для движения в пространстве состояний либо для стабилизации состояния. Вследствие этого не все то, что принято считать и называть ресурсами, будет рассматриваться в этом качестве в данных материалах, например:

=> широко используемый термин «информационный ресурс» ресурсом не является, так как в процессе использования информации она не тратится, хотя и используется. По мнению автора, так называемый «информационный ресурс» корректнее именовать «информационным банком» или «источником информации» либо «генератором информации», более того, имеющаяся в распоряжении объекта информация, образует информационный контент, который следует рассматривать как самостоятельный объект или подсистему объекта;

=> не менее популярный термин «человеческие ресурсы» также, по мнению автора, не является приемлемым. Следует отметить, что существует значительное количество субъектов, которые готовы радостно для решения какой-либо задач губить человеческие жизни в количествах неимоверных. Но, с точки зрения анализа объектов и систем, люди являются системообразующим элементом, поэтому, если при решении каких-либо задач происходит выбытие этого элемента, то это является вырождением систем и не иначе.

Но, чтобы не выглядеть совсем уж строгим, автор готов согласиться, что такие свойства объекта, как энергия или финансы могут вполне считаться ресурсами.

1.4.3.2. Многопользовательское потребление ресурсов.

При многопользовательском потреблении услугами ресурсного параметра могут пользоваться несколько ресурсозависимых параметров.

При этом каждый из таких параметров использует ресурс по-своему, т.е. существует своя функциональная зависимость, связывающая скорость (интенсивность) потребления ресурса и скорость движения по соответствующему параметру или величину стабилизируемого параметра.

Автор полагает вполне корректным отслеживать динамику изменения и потребления ресурса независимо по отдельным ресурсозависимым параметрам, определяя для каждого параметра присущие ему прогнозируемую величину запаса ресурса (прогнозируемый расход ресурса), прогнозируемую среднюю скорость использования ресурса, текущую среднюю скорость использования ресурса и т. д.

На основании полученных величин можно определить аддитивно прогнозируемую величину запаса (расхода) общего многопользовательского ресурса.

Общая прогнозируемая величина расхода общего ресурса при знании времени операции позволит определить прогнозируемую среднюю скорость использования общего ресурса либо такой же результат может быть получен аддитивно из частных прогнозируемых средних скоростей используемых частей ресурса.

Также аддитивно могут быть получены и другие общие скоростные показатели и показатели интенсивностей, позволяющие оценивать корректность использования общего ресурса.

1.4.3.3. Множественное потребление ресурсов.

Под множественным потреблением ресурсов понимается случай, когда ресурсозависимый параметр для своей поддержки (движение или стабилизация) требует использования нескольких видов ресурса.

Этот случай не порождает каких-либо проблем, так как вопросы потребления и резервирования ресурсов будут рассматриваться независимо для каждого ресурса.

1.4.3.4. Дополнительные аспекты генезиса ресурсов. Текущее состояние ресурса

Текущее состояние ресурса в общем случае определяется текущим положением объекта в пространстве состояний, а точнее говоря – функциональной зависимостью между величиной смещения объекта в пространстве состояний и величиной изменения ресурса, процессами утечки и восполнения ресурса за период наблюдения, за который происходит смещение, и состоянием ресурса в момент начала наблюдения (или начала смещения объекта).

Если выражением (25.1) обозначить функциональную зависимость изменения данного ресурса (обозначение изменения см. 12/1) от величины смещения (см. 11/1) за период наблюдения (см. 8/1) следующим образом:

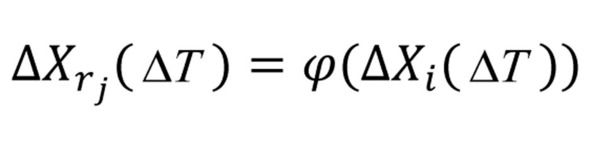
выражение 25.1

а символами (см. 13/1) обозначить величины восполнения и утечки ресурса соответственно, происшедшие за временной период, требующийся объекту для совершения смещения (или период наблюдения), а через R0 обозначить состояние ресурса в момент начала наблюдения, то в итоге можно записать выражение (25) для состояния ресурса по окончании смещения:

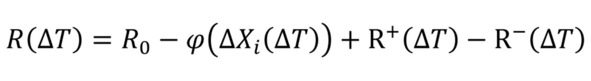
выражение 25

Производя формальную замену интервала смещения на текущее смещение, а интервала времени на текущее время от начала наблюдения, можно получить выражение (26) для текущего состояния ресурса:

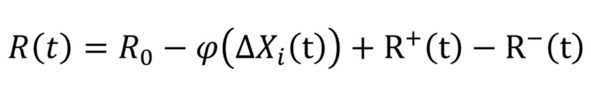
выражение 26

1.5. Системный потенциал. Рельеф пространства состояний

Следует отметить, что в настоящий момент этот раздел имеет статус простого замечания.

В предложенной автором материалов концепции пространства состояний есть определенный недочет, состоящий в том, что все состояния контента в рамках предложенного взгляда представляются равно-статусными.

Но вполне оправданным будет, по мнению автора, придерживаться того, что для любого объекта не все доступные состояния равно-предпочтительны.

Более того, можно допустить, что какие-то состояния показаны объекту, какие-то противопоказаны, какие-то следует признать опасными и т. п.

Для характеристики различной предпочтительности доступных объекту состояний предлагается показатель, в дальнейшем именуемый системный потенциал.

Суть показателя состоит в том, что более качественному состоянию соотносится более высокий системный потенциал, а менее качественному состоянию – более низкий потенциал.

Оценку системного потенциала, в первом приближении, можно произвести через параметры объекта следующим образом:

– среди значений параметров выделяются группы, интервалы, субинтервалы и отдельные значения по следующим признакам:

а) позитивные – показаны в качестве возможного состояния объекта;

б) негативные – не рекомендуются в качестве возможного состояния объекта;

в) нейтральные.

– позитивные и негативные значения всех параметров, определяющих конкретное состояние объекта, складываются алгебраически (нейтральные не участвуют).

– полученный результат, который может оказаться положительным, отрицательным или нулевым числом, собственно и является системным потенциалом состояния объекта.

В результате проведенной операции над объектом, каждому состоянию объекта оказывается сопоставлен показатель – системный потенциал.

Если количество параметров объекта равно N, то данный показатель образует (N+1) -ое измерение.

В этом расширенном пространстве сформируется определенная картина, которую в дальнейшем будем называть рельефом пространства состояний.

Простейшая трактовка рельефа пространства состояний может быть такова:

– из всех возможных неуправляемых направлений движения объектом будет выбрано то, которое ведет к снижению потенциала, а если таких направлений несколько, то будет выбрано то, которому соответствует наибольший градиент снижения;

– если картина представляет из себя поверхность (с количеством измерений N) с нулевым градиентом, то такой рельеф соответствует изотропному пространству состояний, т.е. пространству с равно-статусными состояниями, в противном случае пространство состояний следует считать анизотропным;

– области разрывов и междискретные интервалы по какому-либо параметру можно рассматривать как потенциальные ямы по данному параметру.

На рисунке 12 представлено несколько примеров рельефа пространства (координата Y) состояний для монопараметрической системы (координата X).

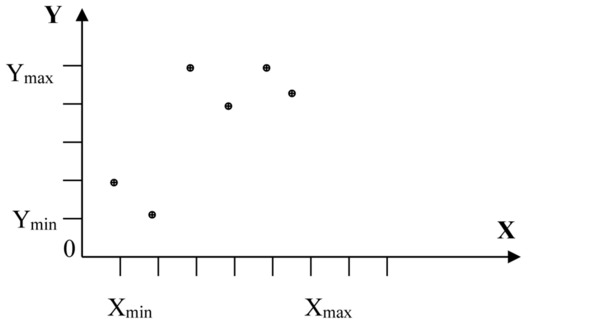
Рисунок 12.1 Рельеф пространства состояний дискретной системы

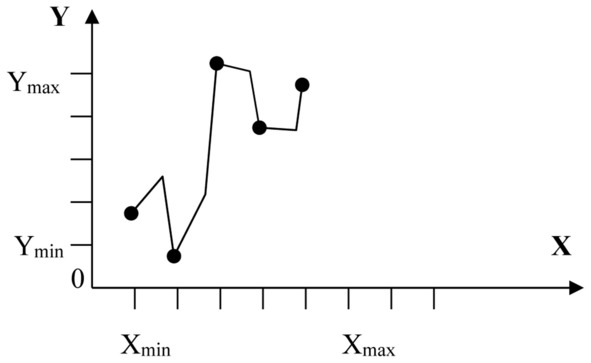
Рисунок 12.2 Рельеф пространства состояний непрерывной системы

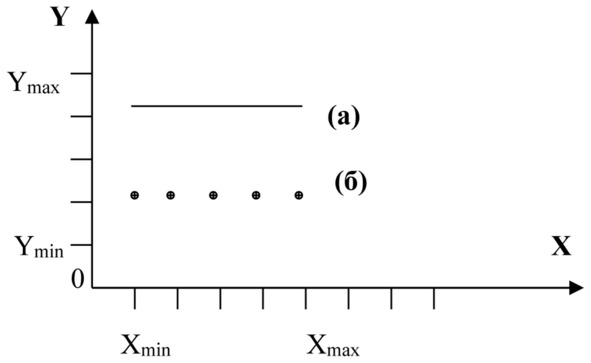
Рисунок 12.3 Рельеф изотропного пространства состояний: (а) непрерывного и (б) дискретного

В заключение автор должен констатировать, что он не готов с пеной у рта защищать и отстаивать предложенный способ оценки системного потенциала. Не исключено, что в дальнейшем способ претерпит изменения.

Но само понятие системного потенциала будет достаточно широко использоваться в дальнейшем.

1.6. Особые виды поведения объектов

1.6.1. Сброс, терминальное состояние.

Наблюдая за генезисом систем можно иногда наблюдать как объект, достигнув определенного состояния, мгновенно (сравнительно с системным временем наблюдателя) переходит в другое состояние с одновременным снижением значений ряда параметров, при неизменности других параметров.

В качестве примера можно привести следующие варианты:

– выстрел или взрыв;

– падение с крыши.

Под сбросом будем понимать, с одной стороны, разрыв в рельефе пространства состояний со ступенчатым снижением системного потенциала, а с другой стороны – неуправляемое движение объекта в этом разрыве.

На рисунке 13. изображен сброс (по направлению от точки A к точке B) с точки зрения системного потенциала.

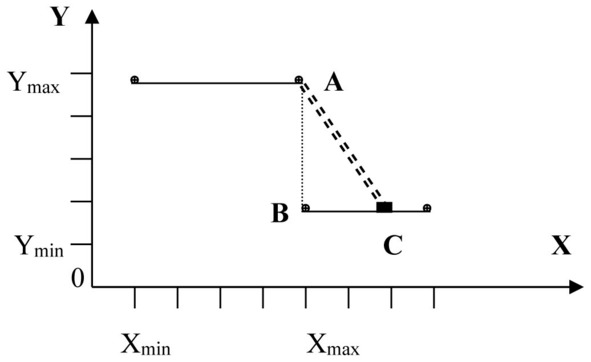
Рисунок 13. Сброс

Сброс может иметь место в системах с пространством состояний любого типа, но в дискретных, дискретно-непрерывных контентах и контентах с разрывами к обычным сбросам добавляются потенциальные ямы, которые в сущности те же сбросы, тем более если движение в междискретных интервалах или разрывах происходит со снижением системного потенциала или объект просто застревает в них.

При движении в области сброса объект, по определению, движется неуправляемо, его движение в этот отрезок времени является результатом только того воздействия, которое было на него оказано в последнем перед сбросом состоянии (то есть объект движется по инерции).

Очевидно, что для перехода системы в область сброса достаточно минимального воздействия, достаточного для вывода системы из области разгона.

В соответствии с понятием системного потенциала, движение в области сброса должно сопровождаться скачкообразным уменьшением значений позитивных параметров, вплоть до полного отключения некоторых параметров, и/или аналогичным ростом значений негативных параметров.

Последнее перед сбросом состояние (точка A на рисунке 13) в дальнейшем будем называть пограничным или терминальным, первое состояние после области сброса (точка B на рисунке 13) будем именовать соответственно пост-терминальным.

Параметр или группа параметров, по которому производится фиксация сброса (параметр X на рисунке 13), будут называться параметрами фиксации.

В качестве заключения отметим, что в реальных системах сброс может иметь ту или иную степень пологости (сдвоенная пунктирная линия AC на рисунке 13), в этом случае сброс может быть квалифицирован как таковой только при условии, если изменение параметров фиксации будет много меньше (не менее, чем на порядок), чем изменения параметров, формирующих сброс.

1.6.2. Трансформации и модификация систем. Вырождение систем и самовырождение систем

При наблюдении систем в генезисе можно отметить существование явления, при котором система, покинув некоторое состояние, принципиально не может в него возвратиться либо в процессе движения теряет часть своих свойств.

Возможен и иной процесс, при котором система начинает проявлять новые свойства.

Подобные явления модификации свойств объектов могут проявляться не только в связи с движением объекта в пространстве состояний, но и в случае существования объекта в стабильном состоянии, просто разворачиваясь во времени.

Причины, которые ведут к возникновению таковых ситуаций, могут быть, естественно, различны и, по мнению автора, группируются следующим образом:

– трансформация системы, приводящая равно как к изменению интервалов доступных значений параметров, так и к изменению набора параметров вообще. В эту группу могут быть зачислены явления широкого спектра:

а) развал системы приводит к сокращению числа параметров системы, вплоть до ее полного исчезновения. В свою очередь присоединение новых элементов приводит к появлению (в общем случае) новых параметров. Правда, если рассуждать строго, система с изменившемся набором параметров является уже совершенно другой системой,

б) самопроизвольное либо индуцированное уменьшение или увеличение интервалов доступных значений параметров. Такое происходит в случае естественного износа (инфляции) систем либо в случае автоматического развития (рост детей, например) либо прогрессивных мутаций, либо какого-либо воздействия со стороны окружающей среды.

Процесс самопроизвольного уменьшения числа параметров и/или уменьшение величины интервалов значений параметров принято называть вырождением, инфляцией системы.

Существуют виды систем, наиболее ярким примером является биологическая система, у которых переход в какое-либо состояние приводит к уменьшению интервалов значений параметров таким образом, что предыдущее состояние выбывает из пространства состояний. Системы такого типа называются системами с самовырождением или самовырождающимися системами.

– исчерпание невозобновляемых ресурсов. При движении в пространстве состояний при условии обязательного использования того или иного ресурса, как явствует из рисунка 11, каждый акт движения приводит к появлению корректирующего смещения вниз относительно целевого смещения. Любая попытка подняться к цели приводит к еще большему углублению вдоль оси параметра ресурса. В результате действия этого фактора объекту оказываются недоступны все состояния выше траектории и все пройденные состояния, по которой вынужденно движется объект, что схематично проиллюстрировано на рисунке 14:

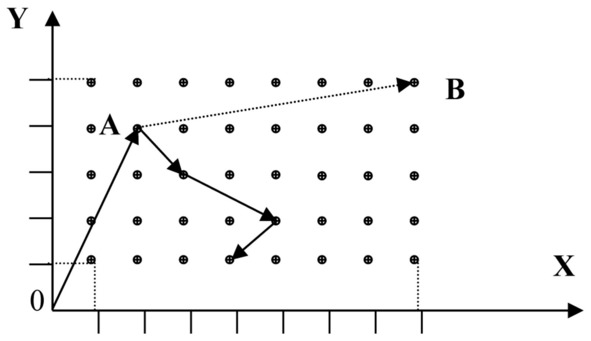
Рисунок 14 Движение с использованием ресурсов

— принципиальная однонаправленность генезиса систем, которая состоит в том, что системе в принципе запрещено возвращаться в исходное или предыдущее состояние, равно как и принимать определенные состояния путем выработки или установления наборов правил или запретов, хотя теоретически и технически, исходя из интервалов значений параметров, объект мог бы принять табуированное состояние. Наиболее яркими примерами могут служить либо движение пешки по доске (пешка не может, как известно, возвращаться), либо система запретов в обществе, либо старение людей.

– организация объекта такова, что пространство состояний содержит не все принципиально возможные состояния, исходя из интервалов значений параметров самого объекта. Эту ситуацию легче проиллюстрировать, что и сделано на рисунках 15.1 и 15.2:

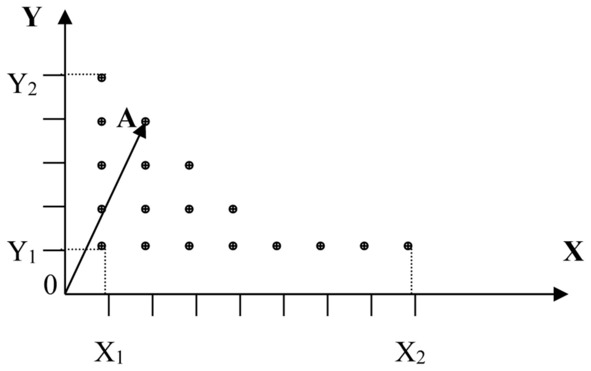
Рисунок 15.1 Пространство состояний – треугольник

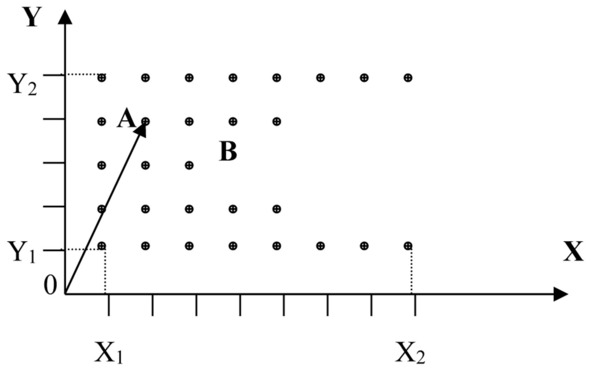
Рисунок 15.2 Пространство состояний – рукава

Как видно из представленных рисунков, если в пространстве состояний присутствуют вычеты, то в таком контенте объект не сможет принимать все теоретически доступные состояния.

Кроме того, рисунок 15.2. иллюстрирует вариант вырождения пространства – после того как объект пройдет точку B, являющуюся точкой разветвления, и попадет в один из рукавов (при условии их сужения), то каждое движение по рукаву будет оставлять объекту все меньше вариантов дальнейшего продвижения.

Следует отметить, что примеры на рисунках 15 не исчерпывают все возможные варианты пространств состояний с исключениями.

1.6.3. Замечание.

В качестве замечания к вопросам об особом поведении объектов следует отметить, что в реальных системах могут иметь место все рассмотренные в данном разделе факторы, затрудняющие существование систем.

Более того, автор не исключает возможности того, что в данном разделе приведены не все источники и факторы, которые могут приводить к ухудшению генезиса объектов.

1.7. Инерционность объектов. Движение объектов

1.7.1. Инерционность объектов.

Все реальные объекты обладают таким свойством как инерционность.

Инерционность проявляется в том, что старт перехода в другое состояние и равно завершение перехода в требуемое или целевое состояние из предшествующего происходит не мгновенно, а требует конечного времени.

В случае, когда объект совершает то или иное движение, при изменении воздействия инерционность проявляется в задержке начала изменения направления вектора и/или модуля вектора движения, а в случае нахождения объекта в состоянии покоя до появления воздействия инерционность проявляется в задержке начала движения объекта в диктуемом направлении. Оба случая позволяют говорить о статической составляющей инерционности объектов.

Статическая составляющая инерционности объектов аналогична массе покоя в элементарной физике.

Динамическая составляющая инерционности проявляется в конечности ускорения движения при наличии постоянного воздействия на объект (смотри выражение 13).

Это приводит к появлению либо зон разгона и торможения, либо конечных времен разгона и торможения.

Вне зависимости от генезиса объектов инерционность проявляется всегда, но сложность строения объектов оказывает влияние на характер инерционных процессов.

Простейшие пассивные объекты, у которых отсутствует система управления, проявляют естественную инерционность по параметрам, которая определяется тем, что при наличии целевого вектора (внешнего воздействия) требуется некоторое время для того, чтобы такое количество компонентов объекта приобрело целевой вектор (или такое количество элементов объекта в случае однородных систем) и начало движение в направлении цели, которого будет достаточно для того, чтобы началось перемещение объекта в требуемом направлении как единого целого в соответствующем пространстве состояний.

В случае необходимости совершить торможение, под инерционностью будет пониматься время, которое необходимо для того, чтобы достаточное количество элементов или компонентов объектов приобрели вектор торможения, обеспечивающее (имеется в виду количество) начало торможения объекта как единого целого.

В реальных условиях воздействие не производится на все компоненты или элементы объекта одновременно (синхронно, синфазно), первоначально воздействие производится на ряд элементов, наиболее по структуре своих параметров соответствующих структуре параметров воздействия или специально (или по воле случая) являющихся приемниками воздействия.

К тому же величина и направленность воздействия на различные элементы или компоненты объекта могут быть различны.

Передача воздействия на остальные элементы осуществляется посредством внутренних связей (воздействие передается по графу связей). Такая передача занимает некоторое время ввиду задержки сигнала внутри промежуточных элементов и задержки сигнала на стыках элементов.

Эти задержки и обуславливают инерционные свойства объектов.

Следует отметить, что структура объекта (его граф) может быть образована с использованием как жестких структурных связей, так и одновременно с применением слабых связей.

В случае объектов, организованных посредством жестких структурных связей (это объекты, в которых параметры, по которым образуются связи между элементами, имеют одинаковые значения в точках соединения элементов, при этом синхронно и синфазно изменяющиеся в одних и тех же интервалах значений), передача воздействия по графу испытывает задержки только внутри составных элементов объекта.

В случае объектов, организованных посредством слабых связей (параметры элементов, образующих объект, в точках соединения этих элементов имеют значения, которые могут изменяться не синхронно и не синфазно), передача воздействия задерживается не только внутри самих элементов, но и на стыках между ними на время, необходимое для согласования значений контактных параметров. Инерционность таких систем выше, чем систем, образованных из тех же элементов того же количества, но соединенных жесткими связями. Примером таких систем могут служить либо объекты, образованные гибкими соединениями, либо системы, организованные посредством информационных потоков.

В случае объектов, проявляющих признаки параметрической неопределенности или других вариантов дополнительных степеней свободы, когда объект (или его компоненты) в ответ на воздействие стремятся перейти сразу в несколько состояний и/или в состояние, отличное от целевого, такое поведение равносильно появлению дополнительного вектора смещения от целевого вектора, преодоление которого требует дополнительного времени и, объективно, ведет к повышению инерционности объекта.

Следует отметить, что чем более полноценным является внутренний граф объекта (имеется ввиду как можно большее участие как можно большего количества параметров в соединении элементов объекта), тем меньшую инерционность проявляет объект. Предельным случаем являются полносвязные объекты – это объекты, все элементы которых жестко связаны между собой по всем параметрам. Если элементы такого объекта однородны, то величина инерции пропорциональна количеству этих элементов.