Некоторые аспекты оценки эффективности функционирования систем. Вторая редакция, исправленная и дополненная

Тогда влияние факторов можно отобразить выражением (38):

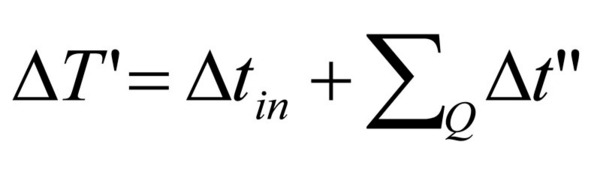
выражение 38

Данное выражение можно трактовать следующим образом – общее отклонение от графика движения, взятое со знаком, является алгебраической суммой отклонений от графика движения, вносимых различными факторами, с учетом инерционных факторов (выделенных в отдельное слагаемое ввиду того, что именно инерционность является предметом данного параграфа), также взятых со знаком.

Необходимо также отметить такой интересный нюанс, как то, что величину отклонения скорости от запланированной величины (или значения времени от запланированного графика движения) можно трактовать как ошибку функционирования, что позволит, при необходимости, оценивать влияние инерционности с помощью выражений, разработанных для оценки ошибок функционирования.

Для разработки аналитических выражений оценки влияния инерционности на движение объекта необходимо рассмотреть общий алгоритм движения объекта (объект, для полноты представления, снабжен когнитивной системой управления).

Кроме того, сделано то допущение, что инерционность является имманентным свойством объекта, определяемым его текущим состоянием, фиксируемым на момент оценки инерционности. Это означает, что оценка инерционности будет производится в условиях отсутствия непосредственных взаимодействий с окружающим миром, которые накладывают отпечаток на характер движения, но могут быть представлены как суперпозиция с устремлениями самого субъекта. Если же внешний мир оказывает воздействие на систему управления и значения параметров таким образом, что это сказывается на инерционности объекта, то это противоречие, могущее иметь место, снимается тем, что инерционность, как указано выше, определяется именно текущим состоянием объекта.

Кроме того, статическая инерционность представлена в виде времен задержки, а динамическая составляющая – в виде ускорения, определяемого в соответствии с выражением (13) и статьей 5.

В общем случае в процессе движения объекта существенны следующие аспекты:

A) система управления получает информацию о текущем состоянии субъекта, производит анализ информации, формирует описание ситуации во внутренних терминах, если описание подпадает под стереотип (или подобно существующему стереотипу), то система управления формирует команду управления самостоятельно, без привлечения когнитивной системы, одновременно отправляя в когнитивную систему описание ситуации и сформированной команды управления;

B) если ситуация не стандартна (отсутствует тождественный или подобный стереотип, или подобие невелико), то система управления передает описание когнитивной системе, которая формирует новый стереотип (который содержит в себе описание алгоритма реагирования на ситуацию) и передает его системе управления, которая формирует необходимые команды управления;

C) может вмешаться тот или иной биологический механизм, имеющий свою систему анализа ситуации, взять под контроль когнитивную систему и/или систему управления и способствовать выработке последней команд управления (не отменяя, впрочем, и выработки команд управления самостоятельно);

D) выработанные команды управления при необходимости проходят этап декомпозиции по функциям органов управления и доводятся до исполнительных органов. На указанные процедуры требуется некоторое время, определяющее когнитивную составляющую задержки начала фактического движения (см. 19/1);

E) исполнительные органы принимают команды управления и, при общем подходе, после некоторой задержки (см. 20/1), необходимой для трансформации управляющих воздействий в движение (составляющая задержки исполнения), начинают движение в пространстве состояний, при этом в движении должно начать участвовать определенное количество подсистем и элементов с тем, чтобы их совместное движение преодолело порог минимально необходимого воздействия, что собственно и определит начало движения объекта. Образующаяся при этом задержка по преодолению порога составляет величину (см. 21/1), при этом следует отметить, что задержка по преодолению порога в чистом виде является пассивной инерцией параметров;.

При этом совокупная величина указанных задержек (39) образует величину задержки перехода к движению объекта на старте, при этом задержка начала движения аналогична инерции покоя простейших объектов. Данную задержку в дальнейшем можно именовать статической задержкой старта.

Следует отметить, что частные задержки в каждой отдельно взятой ситуации вполне могут иметь значения, не совпадающие со значениями этих же задержек в других ситуациях;

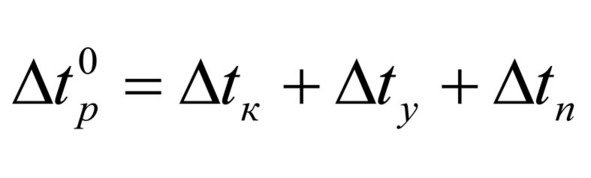
выражение 39

F) после начала движения происходит разгон объекта (субъекта) до расчетного значения скорости движения V0. Исходя из того, что вся дистанция подразделяется на этапы, а прохождение каждого этапа может осуществляться индивидуально (индивидуальность означает, что на каждый этап отводится лимит времени Tod, отвечающий условию (39.1)

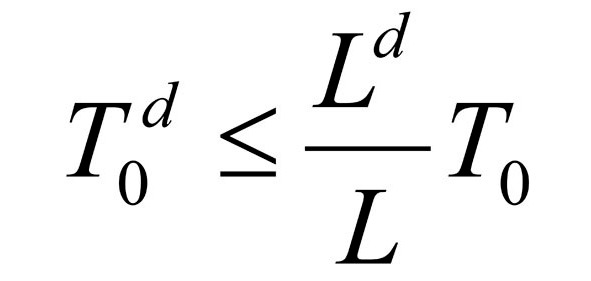
выражение 39.1

где Т0 – общее время, отведенное на операцию, а L – длина трассы, Ld – длина данного этапа), может возникнуть необходимость рассмотрения каждого этапа в отдельности. Но, в дальнейшем, в зависимости от удобства рассмотрения и ввиду не принципиальности отличия всей трассы от одного этапа, не будет проводиться различия между движением объекта по очередному этапу или по всей трассе вцелом (в настоящий момент имеется ввиду расчетная скорость для данного этапа Vod), а рассматриваемый участок будет обозначаться как LI, а время операции для этой дистанции LI будет обозначаться как To’.

Разгон до расчетной скорости осуществляется с некоторым ускорением ap (t), которое может изменяться во времени. Разгон до расчетной скорости (для данного этапа) происходит за некоторое время разгона (см. 22/1), что можно отобразить следующим выражением (40):

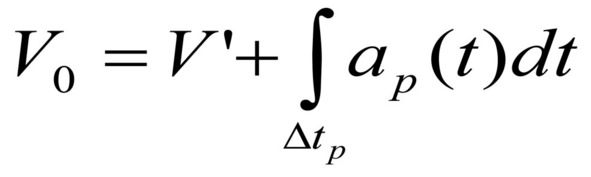
выражение 40

Зависимость ускорения от времени делает вычисления несколько неудобными с инженерной точки зрения, но если протяженности этапов выбрать предельно малыми, то и время, затрачиваемое на их прохождение, будет стремиться к нулю, что позволит принять все ускорения, имеющие место при разгонах и торможениях, постоянными величинами.

Это позволяет привести выражение (40) к хорошо многим известному с детства виду (41):

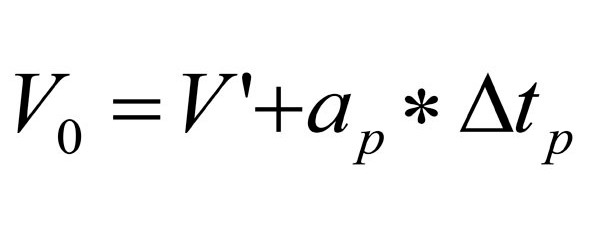
выражение 41

Если бы система могла принять расчетное значение скорости скачкообразно, то за время разгона она прошла бы расстояние, определяемое выражением (42):

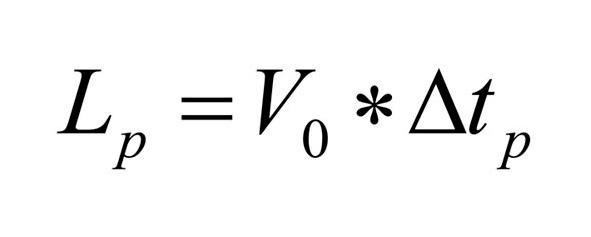
выражение 42

За это же время разгоняющаяся система пройдет меньшее расстояние, так как за весь период разгона скорость будет меньше расчетной. Пройденное расстояние определяется выражением (43):

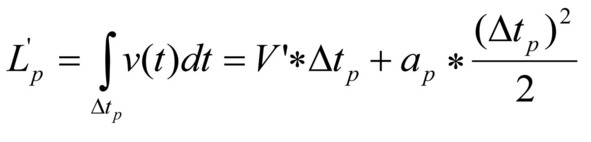
выражение 43

Различие в этих расстояниях определяют задержку (см. 23/1), именуемую в дальнейшем динамической задержкой разгона и необходимую для разгона (а не время разгона (см. 22/1) является задержкой). Время задержки при разгоне определяется выражением (44):

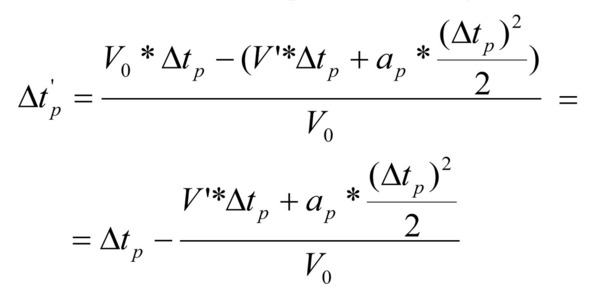
выражение 44

Необходимо отметить, что разницу между расчетным расстоянием и реально пройденным при разгоне следует, для получения времени задержки при разгоне, делить именно на значение V0, так как недостаток расстояния объект должен пройти с расчетной скоростью;

G) сделанные выкладки позволяют определить совокупное время задержки объекта на старте (либо при начале движения после остановки в любой точке трассы) в виде выражения (45):

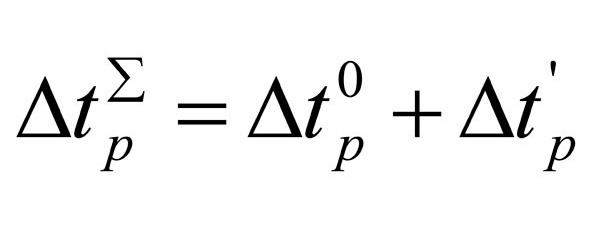
выражение 45

H) по достижении расчетной скорости объект движется к концу этапа (узловая точка или конец дистанции), в конце которого его ожидает (в общем случае) торможение, которое необходимо для того, чтобы система управления могла корректно произвести маневр (при необходимости) либо остановиться без последствий в виде вылета с трассы.

I) по аналогии со стартом, объект не сразу начинает тормозить, но по прошествии некоторого времени, обозначение которого см. 24/1, и которое также складывается из времени, необходимого на оценку ситуации, из времени, необходимого для выработки управляющего воздействия, и времени, необходимого для преодоления порога движения. Но это время задержки начала торможения, в случае, если торможение производится с расчетной скорости, не является существенным, так как, пока система не тормозит, она движется в пространстве состояний по графику, т.е. со скоростью V0. Но начальная задержка перехода к торможению может оказаться существенной, если торможение производится со скорости, превышающей расчетной значение. Поэтому в общем случае начальная задержка (иначе говоря, статическая задержка торможения) (см. 25/1);

J) торможение производится с некоторым ускорением aт (t), которое в общем случае не тождественно ускорению разгона. Для упрощения расчетов, опять-таки, принимается, что этапы между узловыми точками настолько малы, что в их пределах ускорение торможения также можно считать независимой от времени величиной. Торможение производится до некоторой величины VII, которая в частности может быть равна нулю. Торможение происходит за некоторое время торможения (см. 26/1), что можно отобразить следующим выражением (46):

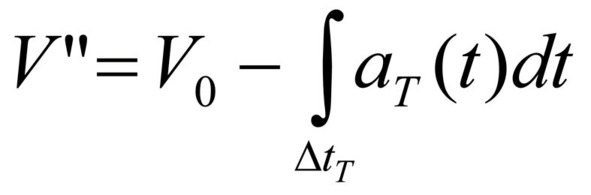
выражение 46

Учитывая замечание о допустимости независимости ускорения торможения от времени, можно выражение (46) преобразовать к виду (47):

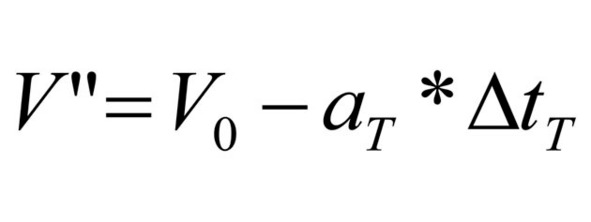
выражение 47

В том случае, заметим, если торможение производится до расчетной скорости, то выражение (47) преобразуется к виду (48):

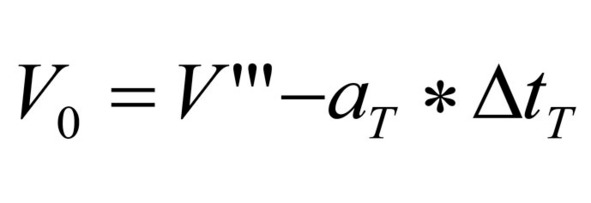
выражение 48

но это выражение будет использовано позже, при исследовании нерегулярностей, вносимых в движение различными факторами.

За период торможения (см. 27/1), двигаясь равнозамедленно, объект проходит расстояние, определяемой выражением (49):

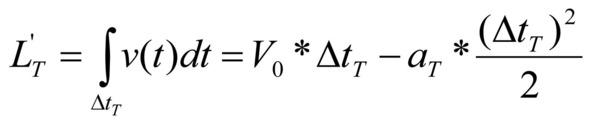
выражение 49

при этом, двигаясь с расчетной скоростью, это расстояние объект прошел бы быстрее, что, собственно, и определяет задержку при движении в условиях торможения (динамическая задержка торможения), которую можно определить выражением (50):

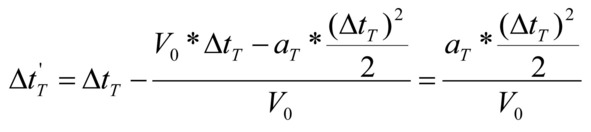
выражение 50

K) сделанные выкладки позволяют определить совокупное время задержки объекта при торможении в виде выражения (51):

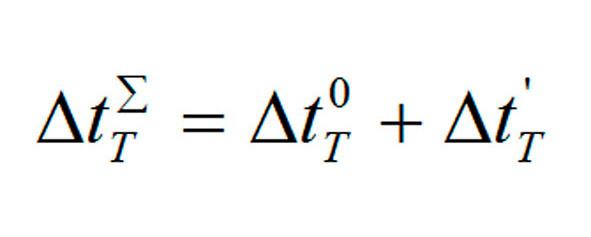
выражение 51

L) выражение (52) определяет общие задержки в движении, имеющие место всегда, даже при отсутствии конфликтов при движении, как то – вылет с трассы, сторонние замедления или ускорения и прочее:

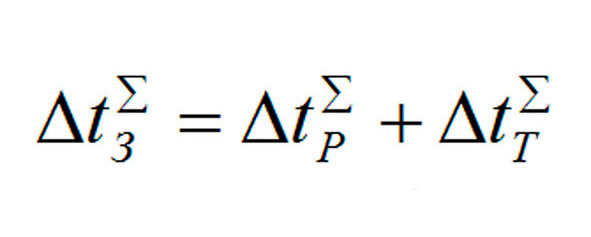
выражение 52

При этом, если допустить, что движение по этапу происходит без эксцессов (вылеты за пределы трассы, перерыв в движении, незапланированные ускорения), то появляется возможность определить эффективную скорость Vэфф движения по дистанции с учетом неизбежных инерционных факторов, которая, естественно, отличаясь от расчетной, обеспечит, тем не менее, достижение финиша (либо конечного, либо промежуточного) в соответствии с отпущенным на операцию временем (53):

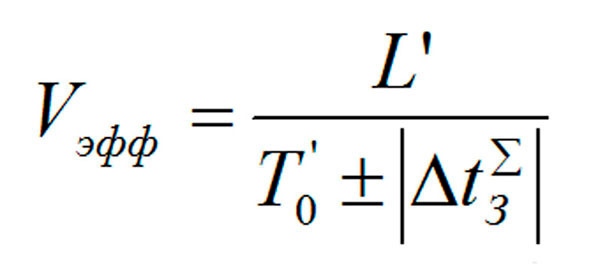
выражение 53

Полученное выражение определяет значение эффективной скорости на момент старта объекта и имеет смысл планируемого значения.

В процессе движения по трассе объект может испытывать различные возмущающие и управляющие воздействия, что будет сказываться на его средней скорости. Кроме того, за время движения по трассе может измениться длина трассы или отведенное на операцию время. Это требует более общего подхода к понятию эффективной скорости.

В более общем виде эффективная скорость может быть определена как скорость, необходимая объекту для достижения цели или прохождения остаточного отрезка трассы за остаточное время из текущей позиции на трассе.

Остаточное время образуется как разница между временем, отпущенным на операцию и временем, прошедшим с начала операции. Время, прошедшее с начала операции, включает в себя периоды стабильного движения по трассе, а также задержки на разгон со старта и совокупности задержек (и/или экономий времени) (см. 17/1), имевших место к настоящему моменту времени. Указанные задержки и/или экономии времени при движении по трассе выступают в виде общего отклонения от запланированного графика движения.

Анализ инерционности показывает, что при планировании движения из данной точки необходимо учесть затраты времени на инерционность при начальном разгоне из данной точки (правильнее говорить о модификации скорости при старте из текущей точки, так как может понадобиться не разгон, а торможение) и торможение в конечном пункте, поэтому выражение для эффективной скорости можно представить в виде (54):

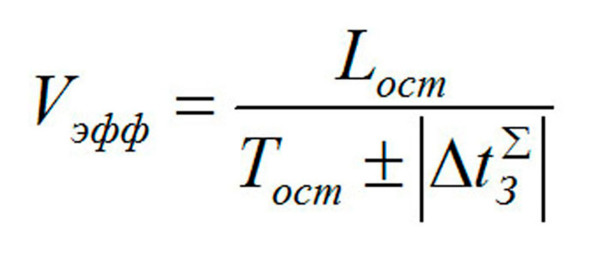
выражение 54

при условии, что остаточное время превышает задержки на маневры, то есть выполняется условие (54.1):

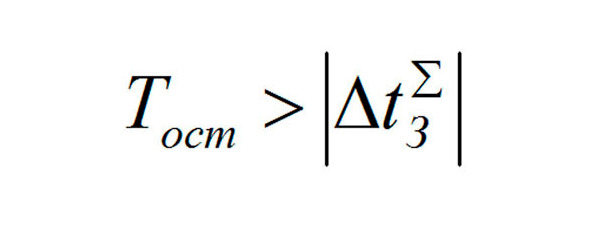
выражение 54.1

Смысл применения знака «плюс-минус» в (54) состоит в том, что если задержки положительны, то их совокупная величина вычитается из времени операции, приводя к необходимому росту эффективной скорости, если реализуется случай, при котором задержки отрицательны (т.е. приводят к ускорению процесса или, иначе говоря, к экономии времени), то эффективная скорость может быть снижена путем прибавления совокупной величины задержек к остаточному времени операции.

Если отсчеты текущего состояния в процессе движения производятся неоднократно, то появляется возможность коррекции эффективной скорости с учетом негативных возмущений;

M) обычная практика перемещений объекта в пространстве состояний такова, что перечень отклонений от планируемого графика движения не обходится стартом в начале движения и торможением на финише, но осложняется различными эксцессами – ускорения и замедления на дистанции, сходы с дистанции, проскакивание узловых и финишной точек, необходимость совершения маневра. В каждом случае тем или иным образом, позитивно или негативно проявляется инерционность объекта. Автор полагает, что есть определенный интерес в рассмотрении этих процессов;

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.