Тензоры. Что может быть проще?

Раз у нас появился нейтральный элемент по умножению в виде единичного тензора, то вполне логично будет рассмотреть понятие обратного тензора. У каждого тензора должен быть тот, который отменяет его действие. Он в некотором смысле противоположен исходному. Компоненты обратного тензора легко можно найти из системы уравнений, которая получается при перемножении двух тензоров, заданного и искомого, и приравнивания их произведения к единичному тензору.

Единичный и обратный тензоры.

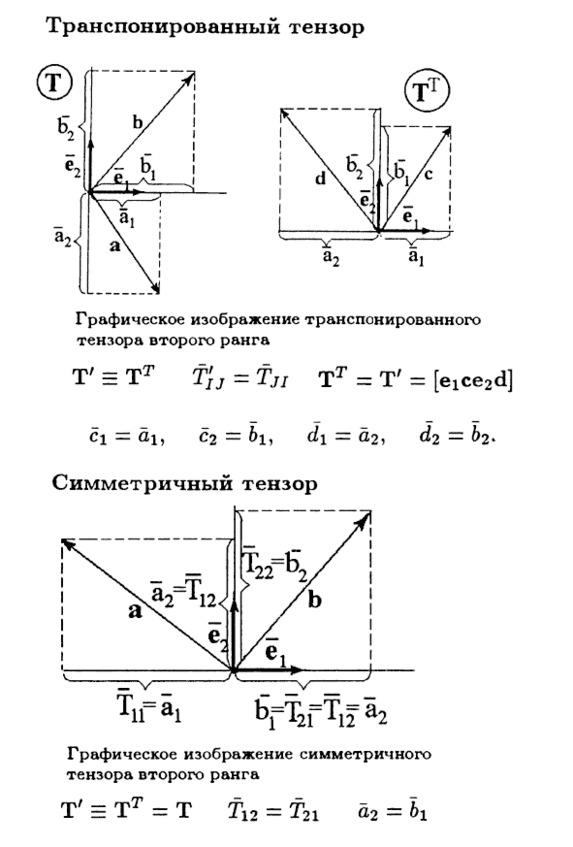
Транспонированный и симметричный тензоры.

Тензор второго ранга является объектом с двумя индексами. Перестановка этих индексов местами имеет специальное название – транспонирование. Это всё равно что вы матрицу из компонент отражаете вокруг её главной диагонали.

Некоторые тензоры не меняются при транспонировании, и их называют, соответственно, симметричными.

Есть такой особый тип тензоров, у которого обратный тензор совпадает с транспонированным. Такие тензоры называют ортогональными. Их воздействие на вектора сводятся к простому повороту на определённый угол, закодированный структурой тензора. У таких тензоров индивидуальные векторы всегда ортогональны друг другу (откуда и название), по модулю равны единице и отстоят от базисных осей как раз на тот угол, на который поворачивают входящий вектор.

Особым типом тензоров является диада. Её можно сконструировать из компонент двух произвольных векторов. Она так и обозначается: как слитая пара букв исходных векторов. Меняя вектора диады местами, мы получим две разные диады. Индивидуальные векторы диады образует второй вектор, масштабированный на три компоненты первого вектора. Итого – три разных вектора, как и должно быть в трёх измерениях, или два для двух.

Ортогональный тензор оправдывает своё название.

Раз есть симметричные тензоры, то могут быть и антисимметричные. Это те, у которых смена местами индексов приводит к смене знака у компоненты. Давайте подумаем, как такое можно изобразить? Ясно, что все диагональные компоненты такого тензора будут равны нолю. Потому что только в этом случае отрицательная величина равна положительной. Таким образом, в трёхмерном пространстве независимых компонент у такого тензора будет всего три, а в двухмерном – две. Значит, этот тензор можно изобразить в виде набора всего трёх компонент – вектора. Или, если мы хотим оставаться в нашей парадигме тензора как набора индивидуальных векторов, можем попытаться понять их вид. Сделать это достаточно просто, если вспомнить про векторное произведение. Действительно! Если взять вектор, в который мы хотели упоковать три независимые компоненты, и векторно умножить его на базисные, то мы как раз получим три разных вектора. И они как раз образуют матрицу, обладающую нужными нам свойствами антисимметрии. Как до этого догадаться? Весьма просто – вспомнить, что векторное произведение само по себе антисимметрично и, следовательно, даст объекты со схожими свойствами.

Где встречаются рассмотренные типы тензоров на практике и что дают? В физике и геометрии различные типы тензоров второго ранга играют ключевые роли, отражая специфические свойства систем и упрощая анализ взаимодействий.

Нолевой тензор, все компоненты равны нолю, в физике моделирует отсутствие воздействия (например, нулевой тензор напряжений в покоящейся жидкости). В геометрии он описывает тривиальные преобразования, не меняющие пространство.

Диада и антисимметричный тензор.

Единичный тензор в физике, в частности в механике сплошных сред, характеризует изотропные материалы, где свойства одинаковы во всех направлениях. В геометрии сохраняет векторы неизменными при преобразованиях (тождественное преобразование).

Транспонированный тензор помогает понять, симметричен ли исходный тензор, а также используется в геометрии при анализе двойственности преобразований (например, в преобразованиях координат).

Симметричные тензоры говорят физикам о законах природы. Например, тензор напряжения нам уже поведал, что уважает третий закон Ньютона, так как является симметричным.

Обратные тензоры позволяют обратить переход от преобразованных векторов к исходным.

Ортогональные тензоры в физике и геометрии описывают повороты и отражения (например, преобразования между инерциальными системами отсчёта). В квантовой механике унитарные операторы (аналог ортогональных) сохраняют вероятности.

Антисимметричный тензор в физике, например, кодирует электрические и магнитные поля (правда, в четырёх измерениях). В геометрии описывает бесследовые деформации (например, чистый сдвиг).

Диадные тензоры – это «кирпичики» для построения сложных тензоров. Их некоммутативность отражает зависимость физических эффектов от порядка взаимодействий (например, сила и плечо в моменте). С геометрической точки зрения они кодируют направленные взаимодействия. Например, в механике деформация материала может быть описана как комбинация растяжений и сдвигов, заданных парами векторов. Любой тензор второго ранга можно разложить в сумму диад.

Таким образом, мы видим, что каждый тип тензора кодирует определённый класс взаимодействий (силовые, вращательные, деформационные), что говорит нам о их вездесущем присутствии в нашей жизни.

Высшие ранги

Давайте сделаем ещё один шаг. Спросим себя, как понять, что перед нами тензор более высокого ранга и как его можно изобразить? Что такое, например, тензор третьего ранга, где с ним можно столкнуться? Наверняка вы в быту уже сталкивались с явлениями, описываемыми этими штуками, если держали в руках пьезовую зажигалку. Когда вы сжимаете некоторые виды кристаллов, их заряды разделяются, создавая электрическое поле. Мы в буквальном смысле выжимаем электричество из кристаллов. Это называется пьезоэлектрическим эффектом. И в значительной степени создаваемое электрическое поле пропорционально силе сжатия или приложенному механическому напряжению. Таким образом, мы получаем уравнение, в котором электрическое поле вроде как с первого взгляда пропорционально электрическому напряжению. И, конечно же, коэффициент пропорциональности называется пьезоэлектрической постоянной. Но присмотритесь внимательно к уравнению и задайтесь вопросом о природе стоящих в нём величин! В левой части у нас вектор, который является тензором первого ранга, а в правой механическое сжимающее напряжение, которое является тензором второго ранга. Так что перед нами уравнение, которое отображает тензор второго ранга на вектор. Так какой же должна быть пьезоэлектрическая постоянная? Подумайте об этом. Она должна брать матрицу и превращать её в вектор. Соответственно, её можно представить как трёхслойный массив чисел. Многомерную матрицу, что ли. То есть она является тензором третьего ранга.

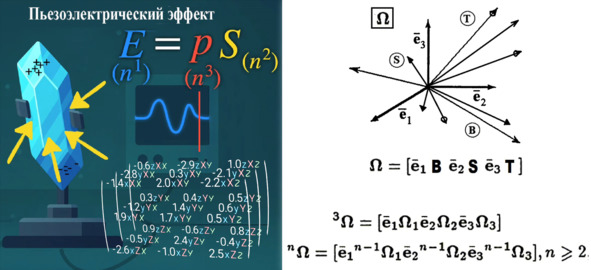
Тензор третьего ранга тоже можно изобразить наглядно.

Таким образом, более высшие тензоры описывают связи, где результат зависит от нескольких направлений (например, пьезоэлектричество требует учёта механического напряжения в плоскости и генерации поля в третьем направлении). Они позволяют ещё точнее описать анизотропию в кристаллах и композитах, у которых свойства зависят от направления, что требует тензоров с большим числом компонент. Тензоры высоких рангов возникают в нелинейных теориях (например, в общей теории относительности). Тензоры ранга три и выше – это инструменты для описания сложных физических, механических и геометрических явлений, где простые векторы или матрицы недостаточны. Они позволяют компактно записывать законы природы, сохраняя информацию о многомерных взаимодействиях и анизотропии.

Подытожим. Опираясь на то, что мы знаем о тензоре напряжений, мы смогли обобщить этот формализм, начав работать с тензорами как с совокупностями векторов. А тензоры высшего ранга стали рассматривать как совокупность тензоров предыдущего ранга. В итоге мы получили шикарный способ описывать физические законы наглядно и просто!

Вектор – это упорядоченные числа. Тензор второго ранга – это упорядоченные наборы векторов. Тензоры старше – это упорядоченные наборы тензоров младше. Всюду наборы наборов. Что может быть проще?

Тензорное произведение

Когда-то мы игрались со счётными палочками и вникали с помощью них в суть сложения и умножения. Было всё просто и понятно. Если из общей кучи вытащить по две палочки три раза, мы получим шесть палочек. Можно вытащить три палочки два раза, и результат будет тот же. Умножение после этого казалось таким простым и понятным. Но потом мы узнали, что под ним подразумевается нечто большее – композиция, или иной способ сопоставления двух величин, порождающий третью. Куда-то канула даже коммутативность умножения. А в некоторых особо запущенных случаях (седенеоны) и ассоциативность. Чем нас может порадовать сочетание изучаемых нами объектов – тензорное произведение? Можем ли такая же наглядность, как у счётных палочек, быть совместима с тензорным умножением?

В этом разделе мы рассмотрим тензоры больше с алгебраической точки зрения. Мы увидим, как их можно порождать за счёт специальной операции – тензорного произведения, и также узнаем некоторые его разновидности.

Суть новой операции

На самом деле мы с вами уже производили операцию тензорного произведения. Только её так не называли. Делали её чисто геометрически. Например, когда внутрь вектора вместо чисел воткнули векторы, получив тензор второго ранга. Когда объявили, что тензор следующего ранга – это структура, индивидуальными объектами которой являются тензоры младшего ранга. Всё это было оно – тензорное произведение. Нам остаётся лишь формализовать данную процедуру в алгебраических обозначениях и разобраться с её свойствами.

Суть, примеры и свойства тензорного произведения.

Обозначают тензорное произведение в виде косого креста, вписанного в круг. Оно порождает новые, более сложные объекты не только в тензорном исчислении. Оно перекочевало и в гомологическую алгебру – в столь специфический раздел математики, в котором даже знак равенства является редким гостем.

Тензорное произведение явно некоммутативно. Это становится ясно уже на примере диад, которые уже фактически своим появлением предвещали подобную операцию. Но оно не настолько сложное, чтобы терять ассоциативность и дистрибутивность. Нарушения этих свойств встречаются в очень запущенных случаях у очень суровых математических объектов. Многие свойства тензорного произведения напоминают свойства матричного. Но это оптическая иллюзия. Перемножая тензор второго ранга тензорно на вектор, мы не получим матрицу. Мы получим тензор третьего ранга, который корректнее изображать в виде трёхмерного массива чисел. Но к этому привыкаешь очень быстро.

Совсем легко вычислять и рассматривать тензорное произведение через компоненты. Нам не важно, сколько у них индексов, и сверху они или снизу. Такие произведения дадут компоненты нового объекта, который будет иметь индексы как первого, так и второго множителя. Можно тензорные произведения раскладывать по базисным векторам и ковекторам, которые тоже, перемножаясь, дают новый объект – базис в пространстве тензоров более высокого ранга.

Часто тензорное произведение определяют как факторизацию. Фактор что? Не слышали о таком? Факторизация – это специальная операция, которая проводится над множествами, пространствами разной природы и различными алгебраическими системами.

Итак, факторизация. Нет, это не новый фитнес-тренд и не рецепт смузи. Это математический способ сказать: «Давайте возьмём всё, что у нас есть, и аккуратно выбросим лишнее». В случае тензоров «всё, что у нас есть», – это свободное векторное пространство, порождённое парами векторов (v, w). Представьте, будто вы набрали в корзину всевозможные комбинации v из первого пространства и w из второго, а потом начали их умножать, складывать и скалярами домножать. Получился гигантский «винегрет» из элементов вида

3 (v1, w1) —2 (v2, w3) + (v5, w4).

Но тензорное произведение – не винегрет. Ему нужно, чтобы всё было билинейно, то есть линейно и по v, и по w. А в нашем винегрете пока царит анархия. Например, (v1+v2,w) и (v1, w) + (v2, w) – это два разных элемента, хотя по смыслу они должны быть равны. Вот тут-то и приходит на помощь факторизация – математический аналог строгой диеты.

Только для тех, кто в теме.

Как это работает? Берём наш «винегрет» из формальных выражений – свободное пространство. Делим его на части, склеивая элементы, которые должны быть равными по своей сути. Например, (v1+v2, w) отождествляем с (v1, w) + (v2, w), как бы говоря себе, что это одна и та же конструкция. Это порождает свойство линейности. Далее, a (v, w) склеиваем с выражением (av, w) и (v, aw). Говоря, что это суть одно и тоже, мы даём себе право вносить множитель. Всё, что осталось после этой «уборки», и есть тензорное произведение пространства V на пространство W. Его элементы теперь ведут себя прилично.

Факторизация – это некоторый аналог деления. Когда мы делим число шесть на три, мы как бы тоже делаем нечто похожее на факторизацию. Мы считаем, что шестёрка – это шесть элементов какой-то природы. Грибов, яблок… Деля на три, мы заставляем разделиться всех этих участников шестёрки на группы по три элемента. А потом объявляем, что элементы каждой тройки слились воедино в своей группе. Сколько таких групп получим? Конечно же, две!

В случае факторизации таких объектов, как пространства или наборы буквенных и численных выражений (свободное пространство), мы слепляем в одно целое то, что считаем подобным по нужному нам признаку. Вот и всё.

Зачем так усложнять-то всё? Вводить какие-то формальные свободные пространства, факторизовать? Такова жизнь и математика! После освоения чего-то на понятном уровне возникает потребность шагнуть выше в абстракции и уже там открывать более общие закономерности.

Разновидности и модификации

Тензорное произведение – это как конструктор, который склеивает векторы и тензоры в более сложные объекты высших рангов. Но иногда хочется, чтобы эти объекты обладали уже заведомо дополнительными свойствами: например, не менялись при перестановке индексов (симметрия) или, наоборот, меняли знак (антисимметрия). Для этого математики придумали два специальных «инструмента»: симметричное и антисимметричное тензорные произведения.

Симметричное тензорное произведение превращает два вектора и тензоры старше в симметричный тензор, который не меняется при перестановке аргументов. Обозначается оно кругом с точкой в центре, в точности как символ Солнца в астрономии. Каждый, кто искушён в линейной алгебре, знает, что для определения чего-либо нового достаточно задать его на базисных элементах. Все остальные надстройки подчиняются законам, действующим над базисом. Для симметричного перемножения базисных элементов рассмотрим тензорное произведение первого на второй, затем второго на первый, и сложим их, разделив сумму на два. Аналогичным образом можно строить более сложные симметричные комбинации, только не забывать делить на число всевозможных перестановок из n элементов, то есть на n! факториал.

Антисимметричное тензорное произведение создаёт антисимметричный тензор также гарантированно. Он меняет знак при перестановке индексов. Обозначается оно в виде клина, смотрящего вверх /\, и читается как «клин» или «внешнее произведение». В уравнениях выглядит футуристично, как настоящая математика инопланетян. Основанное на этом символе исчисление было введено Эли Картаном и невероятно упростило некоторые тензорные методы. Это произвело впоследствии настоящую революцию в математике и сейчас ассоциируется с целым отдельным направлением – алгеброй Грассмана.

Опять же, клиновидное произведение строится через базисные вектора, но в этот раз мы после перестановки элементов местами вычитаем один из другого, разность делим на количество слагаемых. Вычитание ведь – это сложение только со знаком минус. Вы ведь помните это?

Разделяй и упрощай!

Вообще, любой тензор можно разложить на симметричную и антисимметричную части. Найти обе из них удаётся, пользуясь тем же принципом, с помощью которого мы строим сами тензорные произведения. Только вместо перемены местами базисных векторов мы меняем индексы у тензоров местами. Такие операции называются симметрированием – когда нужно получить симметричный объект, и альтернированием – когда нужен антисимметричный тензор. Обозначаются они, соответственно, взятием симметризуемых индексов в круглые скобки и обрамлением в квадратные антисимметризуемых индексов. Индексы, не участвующие в данных процедурах, часто отделяются от остальных вертикальной чертой.

Помимо рассмотренных видов умножения, в тензорном исчислении есть ещё произведение Кулкарни-Номидзу. Оно тоже тензорное, ибо порождает объекты высшего ранга. Но данная операция также несёт с собой смыслы, к которым наша психика на данном этапе ещё не готова…

Подытожим. Мы перевели геометрию на язык алгебры. Возникновение тензоров рангом выше из элементов попроще описали чисто алгебраически – тензорным произведением. Эта операция позволяет комбинировать данные из разных источников, сохраняя при этом информацию о взаимодействиях между ними. Например, в физике тензорное произведение используется для описания систем с несколькими взаимодействующими частицами, а в машинном обучении – для обработки многомерных данных. Тензорное произведение является мощным инструментом для работы с тензорами и дублирует геометрические построения на алгебраическом языке.

Тензорное произведение – это как сплести две нити в полотно: каждая остаётся собой, но вместе они держат узор, который не разорвать. Хочешь описать сложное – просто соедини простое. Что может быть проще?

Полилинейные отображения

Математика – это наука об идеях-оборотнях. Задумывались ли вы, как обычная «двойка» меняет свою сущность в зависимости от контекста? Это не просто абстрактный символ. В арифметике она – количество яблок в корзине. В алгебре – результат деления 6 на 3 или логарифм числа 81 по основанию 9. И ординал, и кардинал. В теории колец – элемент, порождающий идеал 2Z в кольце целых чисел Z. Кажется, будто математические объекты наделены магией перевоплощения, оставаясь собой и одновременно превращаясь во что-то иное. «Математика – это искусство называть разные вещи одним и тем же именем», – так выразился Анри Пуанкаре, гений, чьи работы соединили анализ, топологию и философию науки. Его слова отражают суть нашего путешествия: мы будем исследовать, как один объект – тензор – может быть и многомерным массивом чисел, и полилинейным отображением, и элементом тензорного произведения пространств.

Представьте, что вы смотрите на гору с разных сторон: с востока она кажется пиком, с запада – плато, но суть её остаётся неизменной. Так и тензоры. В физике они описывают напряжение в кристалле, в машинном обучении – веса нейронной сети, а в дифференциальной геометрии – кривизну пространства-времени. Их «оборотническая» природа позволяет математике быть универсальным языком, где глубина идеи важнее формы записи. В этой главе мы раскроем, как полилинейность – свойство, сохраняющее структуру при преобразованиях, – делает тензоры ключом к описанию многомерных взаимодействий. Вы увидите, что определение тензора как «многомерной матрицы» – лишь одна из масок, а его истинная суть – в способности связывать векторы и ковекторы, сохраняя гармонию линейности. Пуанкаре напоминал: даже самые абстрактные конструкции рождаются из интуиции. Поэтому, встречая новое определение тензора, спросите себя: «Какая идея скрывается за этим символом?» – и вы услышите эхо его слов: «Красота математики – в единстве многообразия».

Новый взгляд

Мы с вами убедились в необходимости введения тензоров, рассмотрели различные операции с ними, научились получать новые тензоры более высокого ранга с помощью процедуры, которую мы назвали тензорным произведением. Пришло время перейти на новый уровень! Мы перестанем говорить о новых типах тензоров и вместо этого изменим сам подход к уже известным нам тензорам.

Давайте немного порассуждаем. У нас есть векторы и ковекторы. Из этих направленных объектов мы можем порождать тензоры второго ранга, а из них уже тензоры ещё более высокой валентности (валентность – синоним ранга). Какие-то матрицы мы можем породить просто тензорным произведением векторов. Некоторые так не порождаются, но их всё равно можно разложить по базисным матрицам, олицетворяющим базисные тензоры. Поэтому перед нами конструктор, от которого у нас есть все детали! Имея все составляющие, мы можем строить что захотим. И вполне логично на данном этапе ввести альтернативное определение тензоров. Тензор – это совокупность векторов и ковекторов, объединённых с помощью тензорного произведения. И это определение очень хорошее, потому что оно поможет нам упростить жизнь! Многое из того, что мы узнали ранее, мы можем забыть. Потому что это будет автоматически вытекать из нового определения.

Давайте пока отвлечёмся и вспомним, что такое функция. Кто-то скажет, что это график, люди, далёкие от математики, скажут, что это уравнение. На самом деле проще мыслить функцию как некоторое правило, которое гласит, как, зная нечто одно, можно найти что-то другое. Это более адекватное определение понятия функции. Такое правило в математике называют отображением. Действительно, имея график, вы, зная значение одной переменной, легко найдёте значение функции. Имея таблицу чисел, которую используют часто для построения графика, вы тоже можете найти нужные значения как переменной, так и функции. Иногда такое правило можно записать в виде формулы. Функцию можно описать словесно, потому как не всегда понятно, что перед вами написано в уравнении. Например,

y= 3x+1 означает простейшее правило: возьми любое число x, умножь на 3, затем прибавь к результату единицу и получишь значение функции. А если перед вами запись

y = sin x, то человек, не знакомый с функцией синуса, не сможет понять, что от него тут требуется. Ему будет нужен мануал, который описывает следующий квест: построй любой прямоугольный треугольник, один из углов которого равен x, затем противолежащий катет этого треугольника раздели на его гипотенузу и только тогда получишь заветное значение y. А ещё в математике полно функций, которые обозначаются парой символов, а вычисляются так, будто тебе велят: «Продифференцируй несчастный многочлен, найди священный градиент в пятом измерении и принеси его в жертву контурному интегралу – и это ещё не финальный босс». Из всего известного науке зоопарка функций выделяют самые простые – линейные. Ими-то как раз и являются тензоры, если на них правильно посмотреть. Даже больше, они полилинейны!

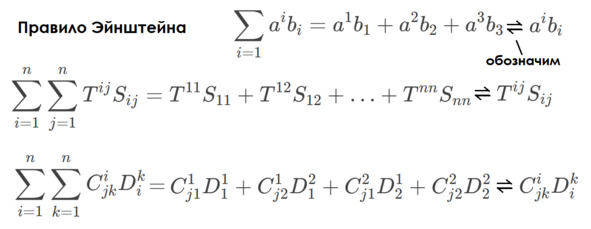
Зачем писать лишние символы когда и так всё понятно?

Итак. Получается, что векторы и ковекторы – это фундаментальные элементы для всех остальных тензоров. Но что делают объекты обоих этих типов? Ковекторы и векторы взаимодействуют друг с другом, выдавая число.

Можно сказать, что ковектор «съедает» вектор, давая число, а можно трактовать это наоборот. Вектор ловит ковектор и выдаёт число. Объекты эти ведь дуальны!

Любой тензор можно разложить по базису и кормить его