Тензоры. Что может быть проще?

Научившись использовать ковектор как функцию и узнав о линейности таковой, давайте попробуем опять понять её геометрический вид, забыв о том, что нам уже известно.

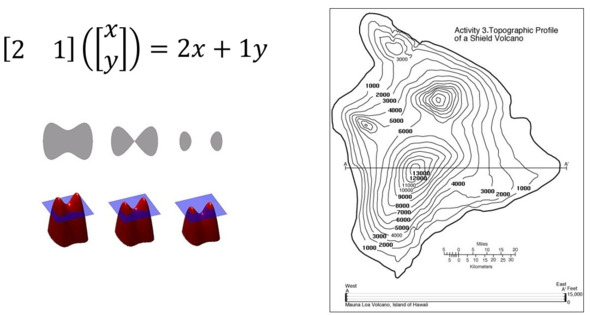
Функция в двух измерениях и способ картографов.

Мы знаем, что обычные векторы мы можем представить в виде стрелок. Но для визуализации функций это не очень удобно. Для геометрической интерпретации конкретного ковектора логично было бы выбрать какой-то один из них и позволить ему воздействовать на любые вектора. Так по деяниям его поймём суть его… Итак, фиксируем ковектор с конкретными компонентами в виде чисел, например [2;1]. А в качестве вектора берём столбец с двумя компонентами x и y, которые могут меняться. Таким образом, мы смотрим на ковектор как на функцию двух этих переменных (x и y). Как мы можем визуализировать функцию от двух переменных, которая выдаёт одно число? Ну что ж. Это очень похоже на проблему, с которой сталкиваются картографы, когда они хотят передать рельеф местности на двухмерном листе бумаги. Когда у вас есть топографическая карта, то вам в основном нужно показать склоны гор и долины, но только с помощью двух измерений. Вот что в этом случае делают топографы: они берут карту и рисуют на ней кривые с постоянной высотой. Так что, просто взглянув на эту карту, мы понимаем, что когда линии идут часто, то склон более крутой. Там же, где линии менее плотные, там местность более пологая, потому что высота меняется не так быстро. Удобно и наглядно! Правда? Так что давайте возьмём и используем эту идею. Возьмём наш ковектор как функцию и спросим себя, где она равна нолю. Спросить в математике означает просто приравнять к нолю нужное выражение, а потом уже угадать недостающие данные. Приравняв наш ковектор, «скушавший» вектор, к нолю, мы получим уравнение на x и y. Оно линейное, и значит, задаёт на плоскости прямую. Теперь спросим себя, где наша функция равна 1, 2, -1, -2 и всем остальным значениям. В итоге мы получим стопку одномерных поверхностей, прямых! Всё в точности как в нашей прежней геометрической интерпретации!

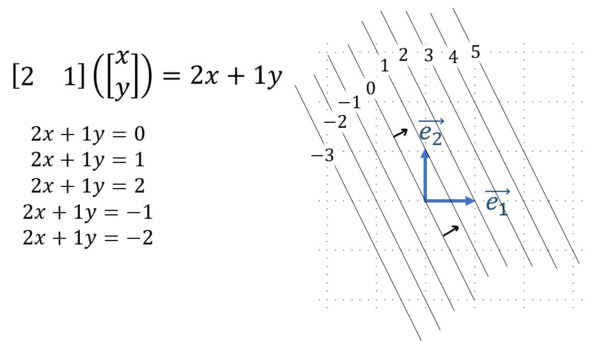
Построение ковектора в двухмерном случае.

Обратите внимание, поскольку наши стопки увеличиваются вверх и вправо, мы можем добавить сюда маленькие стрелочки, как это делали раньше, указав положительное направления для «линий уровня». Всё вышло так, как мы и предположили в прошлых наших рассуждениях. Но это ещё не все приятности! Мы можем научиться воздействовать ковектором на вектор совершенно без алгебраических вычислений, глядя на их чисто геометрическое взаимодействие.

При этом для такого взаимодействия векторов и ковекторов нам не нужно ничего знать о системах координат и компонентах. Мы чертим их на плоскости и смотрим, какое количество стопок пробивает вектор и в каком направлении он это делает. Это количество пройденных насквозь линий и является значением функции ковектора на данном векторе. Если направление вектора и ковектора противоположны, то значение функции будет отрицательным, если вектор идёт вдоль линии ковектора, то он не пробивает ни одной из них, а значит, значение равно нолю.

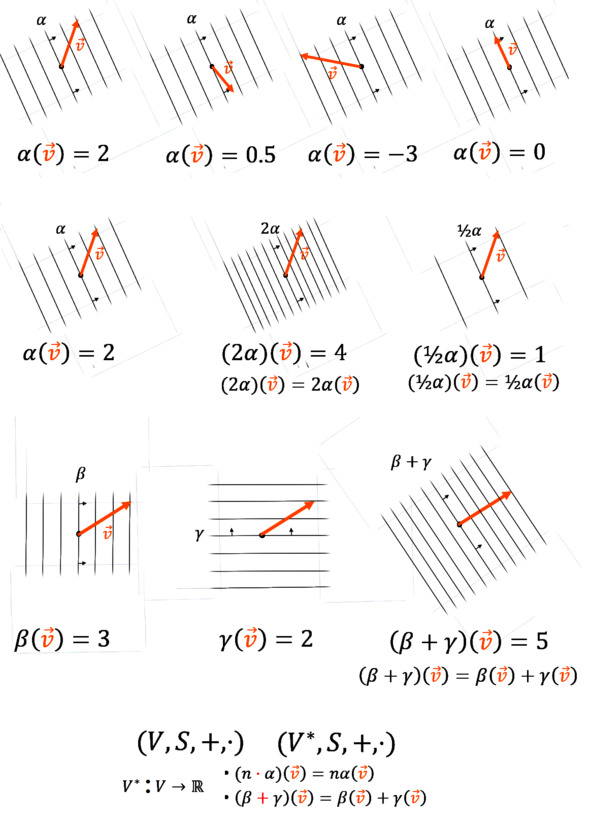
Взаимодействие векторов и ковекторов демонстрируют линейность этих объектов как функций и оправдывают название «дуальных объектов».

Легко в этой интерпретации узреть и линейность данного рода взаимодействий. Всё в точности как в алгебраических формулах, те же результаты для ковекторов и векторов с заданными компонентами. Умножение ковектора на число приводит к увеличению плотности линий, и, поглощая вектор, он вызывает пробитие стрелкой иного количества линий, что приводит к иному результату. Отлично работает и описанное нами ранее геометрическое сложение ковекторов. Непосредственно и наглядно давая полученные из алгебры строк и столбцов результаты.

В связи со всем этим ковекторы можно называть полноценными дуальными объектами. Обычно это обозначают, ставя звёздочку у соответствующего множества (пространства) V векторов, намекая на то, что это уже пространство дуальных к ним ковекторов V*.

Напомним, что есть такая штука, как линейное векторное пространство. Это когда у вас есть куча объектов, которые можно складывать и умножать на числа. Главное, чтобы эти операции можно было менять местами (коммутативность), чтобы они не зависели от порядка выполнения (ассоциативность) и чтобы в наборе имелись ноль и единица. При этом сами объекты могут быть любыми: не только векторы, но и матрицы, функции или ковекторы.

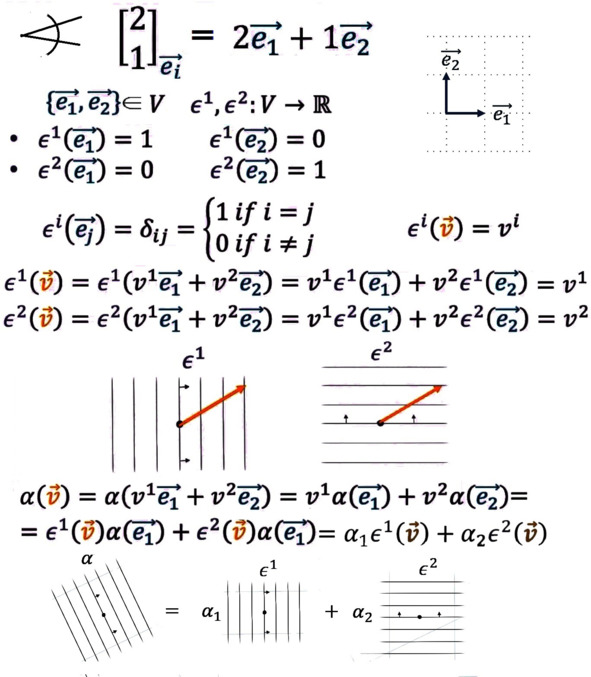
Базисные ковекторы и разложение по ним.

Но раз ковекторы дуальны векторам, а векторы имеют компоненты в некотором базисе, то и для ковекторов можно ввести базис. В качестве такового можно взять любые линейно независимые ковекторы. То есть набор таких ковекторов, каждый из которых нельзя выразить как комбинацию остальных. Линейная независимость является расширением понятия неколлинеарности и некомпланарности на случай большего числа измерений, чем 2 и 3. Но если у нас есть ортонормированный базис векторов, каждый из которых имеет единичную длину и ортогонален остальным, то ему можно сопоставить дуальный, или, как ещё говорят, сопряжённый базис. Он будет уникален для каждого такого набора базисных векторов. Для его получения выбирают такие ковекторы, которые, съедая базисные векторы, выдают в качестве значения либо ноль, либо единицу. Выбрав такие объекты, мы сможем разложить любой ковектор как линейную комбинацию базисных.

Интрига с разными компонентами

Каждый раз, когда имеешь дело с дуальными объектами, невольно задумываешься, чем обусловлена сама эта дуальность. Вспоминаются поговорки про две стороны одной медали и прочие народные премудрости. Не единая ли сущность предстала перед тобой в разных обликах? Что ж, многие знания – многие печали. И на наших новых дуальных знакомых, векторах и ковекторах, нам придётся посмотреть с этой же стороны. А значит, нам придётся опять творить, изощряться и выкручиваться, переводя на корректный и удобный математический язык новые наблюдательные данные.

А поразмыслить действительно есть над чем. Сегодня мы знаем, что по второму закону Ньютона сила является произведением импульса по времени. А значит, по нашей с вами уже установленной классификации сила должна являться вектором. Контравариантным объектом, как и скорость. Если вы решаете задачу о движении тела под действием силы тяжести, то вы можете её найти как производную импульса. Эта операция оставляет контравариантный объект контравариантным. С другой стороны, эту же самую силу можно найти как градиент некоего скалярного поля – гравитационного потенциала. Таким образом, сила предстаёт перед нами классическим ковектором. Но как же так? Не можем же мы приравнять вектор ковектору? Это совершенно разные объекты, хоть и дуальные.

Сила – вектор или ковектор?

Но такова жизнь, и так устроен мир. Придётся принять сей факт и как-то разбираться и с этим. Вышеописанные наблюдения заставляют нас признать следующее: такой объект, как сила, может быть описан и как вектор, и как ковектор. А значит, это единый объект, проявляющий в определённых обстоятельствах одни свойства, а в других – иные. Нам лишь остаётся смириться с этим и, апеллируя к философии дуальности, придумать, как вектору сопоставить ковариантные компоненты, а ковектору – контравариантные.

Что бы вы предприняли, обнаружив данную проблему, если бы были математиками-первооткрывателями? Иногда полезно самостоятельно попробовать решить проблему и поиграть в первопроходца. Это очень сильно углубляет понимание, и полученные потом знания остаются с вами навсегда, становясь частью вас.

Итак, у нас есть объект, который имеет направление, но иногда при смене координатного базиса удлиняется, а иногда увеличивает плотность, сохраняя свою как бы длину. Как и то, и другое приписать нашему направленному куда-то нечту? В вопросе, как всегда, содержится часть ответа. Описанное свойство говорит о том, что такая штука, как сила, имеет и те, и другие компоненты. И ковариантные, и контравариантные компоненты. А компоненты – это что? Это всего лишь определённые проекции. Поэтому мы можем поступить так. Будем представлять силу в виде более привычной нам стрелки и попробуем спроецировать её на оси координат двумя разными способами, и посмотрим, как эти два типа проекций меняются при смене базиса.

Для большей общности возьмём косоугольную систему координат. Проведём в ней некоторую абстрактную стрелку a. В таких системах координат базисные векторы друг другу не перпендикулярны, а расположены под острым или тупым углом. Но координатную сетку получают, проводя линии параллельно осям координат, задаваемым базисными векторами. Таким образом, просто опустим из начала и конца вектора линии на наши оси параллельно базисным векторам. Координаты нашей стрелки, полученные этим способом, как раз совпадают с тем, что мы изначально считали координатами вектора. Такие координаты мы называли контравариантными. Вспомните наш пример с карандашом, направленным на дверь. Все его разложения, приводимые в том примере, были как раз контравариантными компонентами карандаша в косоугольных базисах.

Чтобы получить ковариантные компоненты, нам нужно получить проекции вектора на базисные направления. Ведь именно проекция будет обладать нужным нам свойством – меняться согласованно с изменением самих базисных направлений и масштабов. Для получения ковариантных компонент нам нужно опустить перпендикуляры к нашим осям координат из начала и конца стрелки. Это и будут наши ковариантные компоненты, по сути проекции стрелки на базисные направления. Сразу становится понятным, почему раньше вы не задумывались о дуальной природе компонент вектора. В картезианской (прямоугольной системе координат, названной в честь Картезия, по-нашему – Де'Карта) контравариантные и ковариантные компоненты будут всегда совпадать!

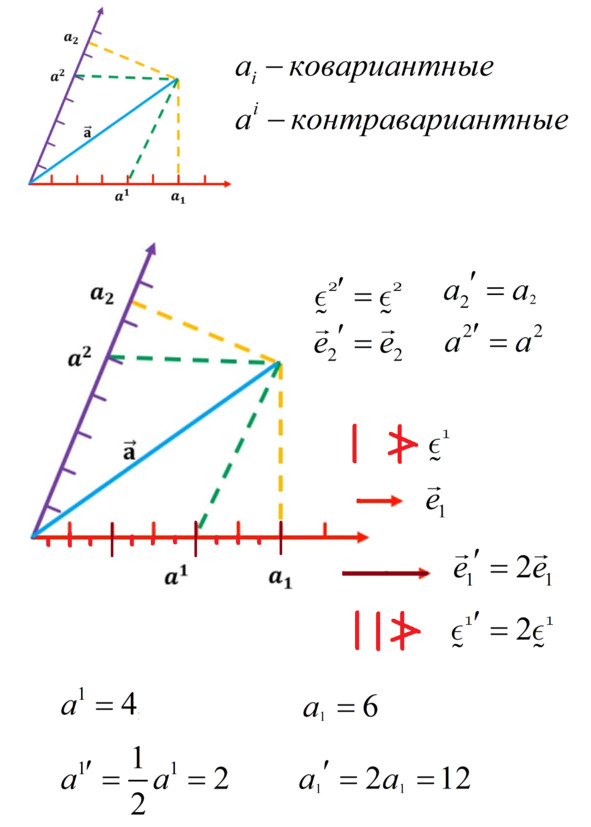
Визуализация контравариантных и ковариантных компонент стрелки и их изменения при увеличении одного базисного вектора и ковектора на горизонтальной оси. Вторая ось и базисные величины на ней остаются неизменными. Штрихом отмечены величины после изменения.

Определившись со способом визуализации ковариантных и контравариантных компонент стрелки, самое время задуматься об обозначениях и утвердить их. Базисные векторы обозначают с индексом внизу. А контравариантные компоненты векторов с индексами вверху. Базисные ковекторы обозначают индексами вверху, а ковариантные компоненты обозначают индексами внизу. Это правило математики ввели, чтобы было удобнее раскладывать объекты на компоненты и дабы индексы были на разных уровнях. Тот факт, что индексы у контравариантных компонент находятся вверху, а у базисных векторов внизу, как бы намекает нам, что они преобразуются противоположным образом. Всё это облегчает восприятие, приятнее суммировать и вероятность запутаться меньше. Сплошные плюсы!

Теперь давайте поиграемся с первой осью нашей системы координат и увеличим базисный вектор в два раза. Видно, что контравариантные компоненты при этом уменьшаются в эти же самые два раза. Контравариантная метка компоненты теперь отсчитывает вдвое меньше базисных масштабов из-за увеличения длины масштаба. Как и должно быть!

А вот ковариантная метка как была воткнута в ось перпендикулярно ей, так и не поменяла своего места. Но зато базисный ковектор увеличил свою плотность в два раза. А значит, численно он увеличивает цену этого же отрезка вдвое! Опять в точку!

Теперь мы можем посмотреть и на другой способ преобразования наших координат – поворот. Две оси поворачивать скучно. Для большей наглядности и информативности давайте чисто визуально в виде стоп-кадров заценим, как по-разному будут вести себя контравариантные и ковариантные компоненты стрелки, если поворачивать, допустим, на этот раз вторую ось.

Пусть изначально оси координат будут ортогональны друг к другу. Затем будем наклонять вертикальную ось вправо-вниз. В этом случае ковариантная компонента неподвижной оси вообще не меняется, а для поворачивающейся следует за изменением её направления, оставаясь всего лишь послушной тенью.

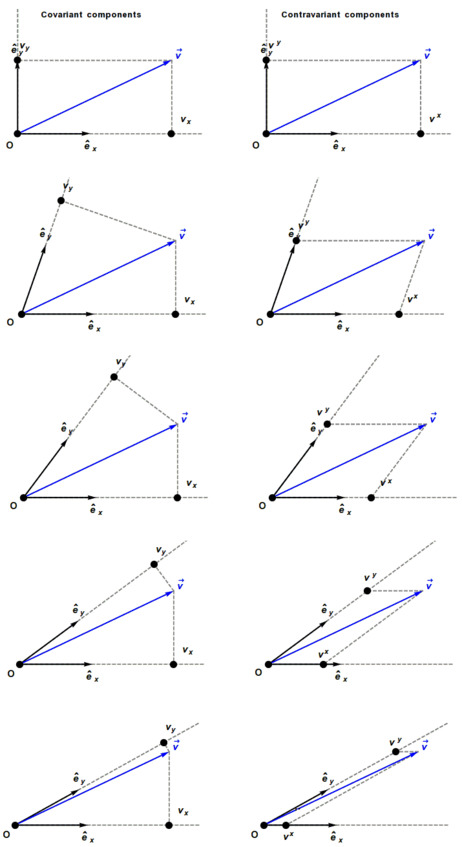
Покорное следование ковариантных компонент, и изворотливость контравариантных!

При этом обе контравариантные компоненты вытворяют пируэты. Даже та, что относится к неподвижной оси. Они делают всё, чтобы из видоизменённых контравариантных компонент можно было бы собрать тот самый исходный вектор.

И вот уже это наблюдение наталкивает нас ещё на одну мысль. Мы можем ковариантные компоненты описать в терминах скалярного произведения стрелки на базисные векторы! Это даст ещё одну алгебраическую интерпретацию и методику вычисления ковариантных компонент.

Итак, наши контравариантные компоненты – это просто коэффициенты, стоящие перед базисными векторами в разложении нашего вектора.

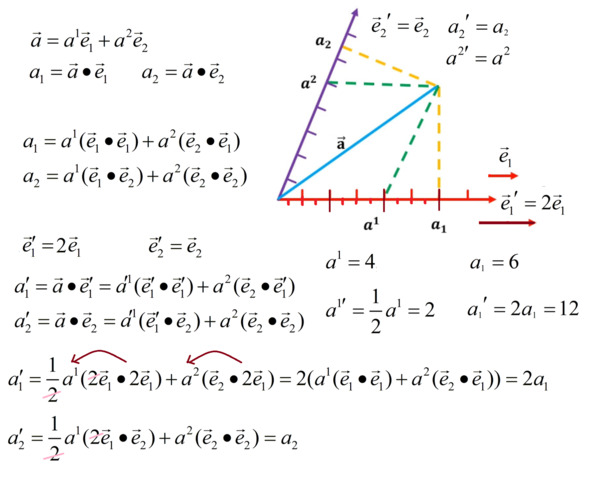
Алгебраически наглядное преобразование ковариантных компонент вектора.

Ковариантные компоненты – это скалярное произведение нашего вектора на базисные вектора. По сути, проекции, тени. Поэтому, когда базис меняется, эти проекции тоже меняются в сторону, следующую за изменением базиса. Только и всего.

Можем для примера вычислить их и увидеть, как масштабные множители, изменившие базис, выносятся, кое-где сокращаются и в итоге дают получить в точности тот результат, который нужен.

Итак, подытожим. Мы с вами увидели, что есть величины, имеющие направление и интенсивность (длину, плотность) как вещи в себе. Их можно мыслить как некие инвариантные объекты, которые, тем не менее, можно представлять разными типами компонент. Компоненты в зависимости от типа преобразуются по-разному. Для каких-то из этих величин ковариантное представление более естественно, для других – контравариантное. Но в силу взаимной однозначности таких представлений нас это волновать уже не должно. Мы научились оперировать с каждым типом компонент как с самостоятельным геометрическим объектом. Получили два вида представления направленных объектов в виде векторов и ковекторов. Что из этого использовать – зависит от задачи. Мы увидели ясно, почему происходит такое разделение. Когда вы движетесь к двери, она движется в противоположную сторону – к вам.

Контравариантность – это дверь, которая «бежит» к вам, когда вы идёте к ней. Ковариантность – это ваши шаги, которые гарантируют: чем больше вы их делаете (в направлении двери), тем ближе она становится. Что может быть проще?

Необходимость введения тензора

Мир вокруг устроен порой весьма сложно. И для исчерпывающего описания явлений, с которыми сталкиваются человеки, одними стрелочками не обойтись. В этом разделе мы с вами естественным образом придём к такому объекту, как тензор. И уже опираясь на этот первый пример, сможем развить это понятие, увидев его элементы и в стрелочках, и в более сложных штуковинах.

Почему вектора не хватило

Представьте, что вы – инженер XIX века, и ваша задача – рассчитать прочность моста. Вы знаете, что сила – это вектор: у неё есть направление и величина. «Отлично! – думаете вы. – Запишу все силы векторами и сложу их!» И тут приходит прозрение: чтобы описать, что происходит внутри материала, вектора недостаточно. Нужен объект, который хранит информацию не только о силе, но и о том, как она распределена по бесконечно малым площадкам, какие в них действуют напряжения. Так начинается история тензоров. Одним из первых примеров тензора ранга больше чем 1 (о рангах позже) был тензор напряжений. Собственно, само слово «тензор» происходит от латинского tensus, означающего «напряжённый».

Напряжение – это мера того, как частицы материала «общаются» друг с другом под нагрузкой. Представьте, что каждая частица – житель многоквартирного дома: Сосед сверху давит на неё (нормальное напряжение); сосед слева пытается выдернуть её с места с доворотом вокруг своей оси (касательное напряжение); и так с каждым из соседей что-то да происходит. Вектор может описать, например, суммарную силу, действующую на весь дом. Но чтобы понять, кто из его элементов кого конкретно толкает, нужна полная сводка по каждому элементу и уровню. Для этого инженеры придумали выделять бесконечно малый кубик материала и смотреть на силы, действующие на каждую из его шести граней.

Отдельно нужно прокомментировать понятие бесконечно малого кубика. Лейбницу и Ньютону часто предъявляли за подобные высказывания. Действительно, что такое бесконечно малый объём? Почему бесконечно малую величину вы иногда считаете не нолём и обращаетесь с ней как с параметром, а иногда отбрасываете как настоящий ноль? В качестве оправдания такого подхода Лейбниц говорил: «Прибавьте к горе песчинку. Вы можете её учитывать, считая частью горы, а можете не учитывать и пренебречь её параметрами в сравнении с величием горы – это и есть бесконечно малая». Исчисление бесконечно малых обогатило человечество колоссальными инженерными достижениями ещё до того, как было переосмыслено и строго непротиворечиво обосновано в трудах Огюстена Коши, Карла Вейерштрасса и других математиков. Это теория пределов и всё то, что вам рассказывают на матанализе. В физике бесконечно малыми считаются реальные (не бесконечно малые!) величины, которые малы в сравнении с другими параметрами системы. Их игнорируют, если их вклад в результат незначителен. Хотя с точки зрения математики с ними работают как в классическом матанализе.

Итак. Представим себе некоторое тело и какой-то маленький элемент внутри него.

Напряжения возникают в теле при его нагружении (деформации, сжатии, скручивании) как реакция частиц на попытку внешних сил изменить их взаимное расположение. Эти внутренние силы сопротивления удерживают частицы от смещения.

В одной и той же точке материала напряжения могут различаться в зависимости от направления. Например, соседние частицы могут «давить» вдоль одной оси и «сдвигать» вдоль другой. В простых случаях, таких как растяжение или сжатие бруса, определить максимальные напряжения относительно легко. Однако при сложных нагрузках задача усложняется: требуется анализировать, как напряжения меняются при повороте условных площадок внутри материала.

Для этого изучают напряжённое состояние – совокупность всех напряжений, действующих на бесконечно малый элемент вокруг точки. Такой подход позволяет найти опасные зоны, где напряжения достигают критических значений, и предотвратить разрушение конструкции. Коротко: напряжения – это внутренний ответ материала на внешние силы, а их анализ требует учёта всех направлений и типов воздействия.

Попытки первооткрывателей справиться с описанием всех этих напряжений, тянущих и сдвигающих точку в разные стороны, были вполне естественны. Кстати, что бы вы сделали на их месте? Как учли бы в едином описании всевозможные силы упругости, действующие на элемент тела?

Наши первооткрыватели первично вводили систему координат XYZ и рассматривали координатные плоскости как основу для бесконечно малых площадочек. Силы, действующие на каждую из площадок, первооткрыватели обозначали максимально просто. Xx, Xy, Xz, Yx, Yy, Yz, Zx, Zy, Zz. Под этими символами подразумевали проекции напряжений, действующих на гранях элементарного кубика или на площадке, соответствующей конкретной оси координат. Вполне естественно выглядит! Согласитесь?

В последствии в XIX веке наступило прозрение, что эти девять чисел – есть единый объект! Его-то и назвали тензором напряжений.

Как видите, всё просто в математике, гениально и просто. Где невозможно обойтись одним вектором, ничто не мешает нам взять их несколько штук!

Сегодня обозначения отличаются от тогдашних. Тензор напряжений принято обозначать чаще всего греческой буквой «сигма» с двумя индексами или латинской буквой P. Первый индекс показывает, о какой грани или площадочке идёт речь, а второй – о каком компоненте вектора напряжения, относящегося к этой площадке.

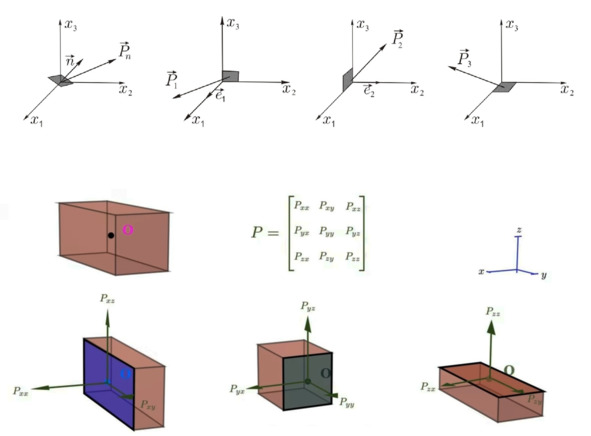
Варианты задания напряжений в трёх направлениях в виде трёх векторов сил, приложенных к конкретной площадке. Можно также рассматривать площадку, заданную произвольной нормалью.

Возможно, вы спросите, почему нельзя просто взять и сложить все эти силы или их компоненты, действующие в одном направлении, приложенных к точке, и получить вектор силы на единицу площади? Почему, например, нельзя сложить Pxx и Pyx? Дело в том, что хотя силы действуют в одном направлении в одной точке, их природа различна. Например, Pxx тянет объект влево и хочет, чтобы соответствующая этой компоненте грань выступала влево. В то же время Pyx действует, чтобы сдвинуть или потянуть выделенную перпендикулярную оси Y грань влево. Эта компонента силы хочет создать трёхмерный параллелограмм вместо выступа. Сдвиг и растяжение приводят к тому, что тело деформируется по-разному в разных направлениях. Поэтому эти компоненты и вектора нельзя складывать. Поэтому же, помимо указания сил, необходимо указывать поверхность, на которую действует сила. Если сложить их «в лоб», получится бессмысленная смесь разнонаправленных векторов. Это как сложить скорость ветра и силу тяжести – формально числа есть, но физического смысла нет.

Представьте кубик, на который действуют: растяжение по оси X, равное 10 МП (Мега Паскалей), и сдвиг по грани XY, равное 5 МП. Если сложить эти силы, мы получим 15 МП, но это не будет иметь смысла: растяжение и сдвиг – разные типы воздействия. Чтобы найти, например, максимальное растягивающее напряжение под углом 30°, нужно использовать тензор, всю совокупность действующих напряжений, а не сумму компонент.

Какой мы теперь делаем вывод из всего этого? Тензор напряжений – это единственный способ корректно описать, как силы распределены по всем направлениям и площадкам в точке материала. Простое сложение компонент:

– смешивает разнородные величины (нормальные и касательные напряжения);

– игнорирует зависимость напряжений от ориентации;

– нарушает законы физики (например, парность касательных напряжений).

Можно привести простую аналогию: Представьте, что тензор – это палитра художника, где каждый цвет (компонент напряжения) отвечает за определённый оттенок. Если смешать все краски в кучу, получится грязно-коричневая масса. Только используя цвета по правилам (тензорный формализм), можно создать точную картину напряжённого состояния.

Исчерпывающее описание

Давайте теперь задумаемся над тем, почему тензора напряжения как совокупности трёх векторов достаточно для описания вообще всех мыслимых и немыслимых напряжений в теле? Всего три вектора, приставленных к трём площадкам, могут решить любой вопрос.

Для этого анализа давайте вспомним доступные нам операции. Мы можем записать три вектора напряжений, приложенных каждый к своей ориентированной площадке, в виде прямоугольной таблицы из девяти компонент, называемой матрицей. Матрицы могут умножаться на другие матрицы, и в частности на матрицы-строки и матрицы-столбцы.

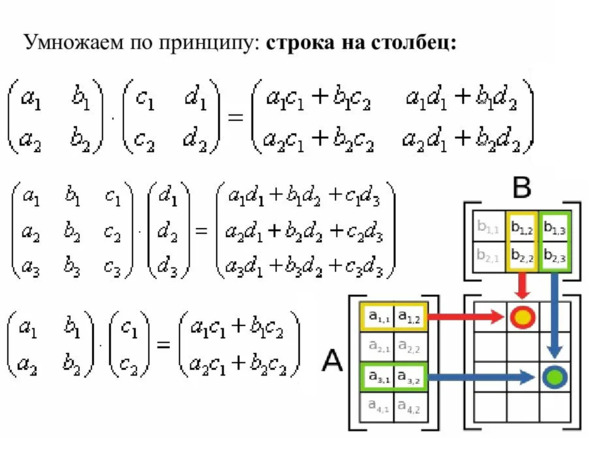
Матрицы умножаются так.

Если из элементов матрицы составить некоторые алгебраические комбинации, то мы можем получить так называемые инварианты – величины, которые будут неизменны при переходе к другой системе координат. На всякий случай напомним, что матрицы умножаются по правилу «строка на столбец». Умножаясь на вектор справа или на ковектор слева, они дают тот же тип объекта (вектор и ковектор соответственно) и в этом смысле являются операторами. То есть объектами, которые преобразуют вектора, превращая их в другие вектора. Матрица – это оператор, то есть превращатель. Если вектора, на которые воздействуем, мы стали рассматривать в новом базисе, то и превращатель разумно тоже рассмотреть с новой точки зрения – из нового же базиса!