Тензоры. Что может быть проще?

Инварианты матрицы: I1 – след,

I2 – вторая симметрическая сумма,

I3 – детерминант.

У вектора при смене базиса не меняется его «длина» или, как её называют в более абстрактном случае, норма. У матрицы тоже есть несколько типов инвариантов. Это её след – сумма диагональных элементов, определитель (детерминант) и сумма главных миноров второго порядка (или вторая симметрическая сумма). Инварианты – это «душа» матрицы. Они остаются неизменными, даже если вы смотрите на объект под разными углами. Как говорил математик Герман Вейль: «Инварианты – это то, что остаётся, когда всё остальное ушло».

Как эти математические действия помогут нам получать информацию из тензора напряжений? Ну, во-первых, сразу видно, что вместо одной длины вектора у нас есть три каких-то инварианта! Каждый из них наверняка расскажет нам о чём-то своём, специфическом именно ему качестве. Во-вторых, матрица оказалась неким преобразователем, который, беря направление (вектор), видоизменяет его. И по деяниям такого оператора можно смело делать выводы о внутренней структуре, закодированной матрицей, олицетворяющей наш тензор напряжений.

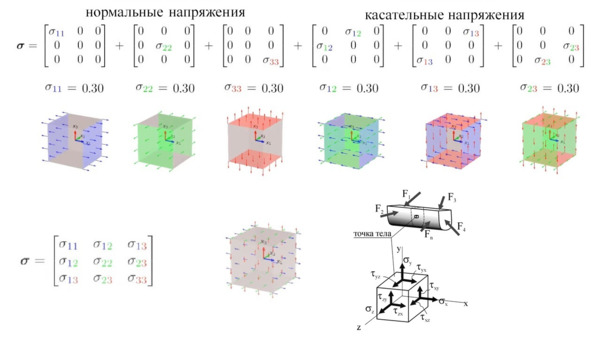
Разложение тензора напряжений на компоненты.

Так почему же трёх векторов тензора хватает для описания напряжений в любом направлении? Всё просто. Тензор напряжений – это не просто три вектора, а математический оператор, который кодирует правила преобразования напряжений при изменении ориентации площадки. Вот как это работает. Три вектора – это базис для всех возможных направлений. Каждый из трёх векторов тензора описывает напряжения на гранях кубика, ориентированных вдоль осей X, Y, Z. Эти направления выбраны не случайно – они образуют ортонормированный базис, то есть охватывают всё трёхмерное пространство. Любое произвольное направление можно представить как комбинацию этих трёх осей. Например, площадка с нормалью под углом 45° к осям X и Y «видит» проекции напряжений с граней X и Y. Тензор позволяет вычислить эти проекции через матричные операции.

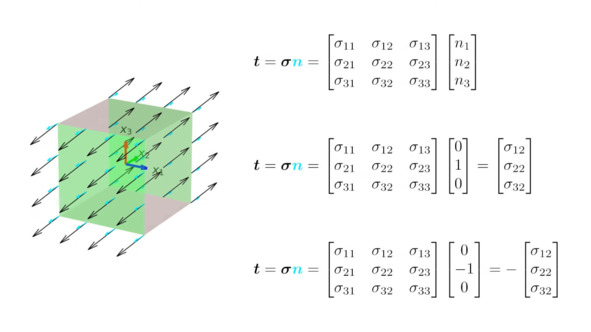
Пронзаем тензор векторами и получаем силу в их направлении.

Тензор – это оператор преобразования. Чтобы найти силу напряжения на произвольной площадке с нормалью

n= (nx; ny; nz), нужно умножить тензор напряжений Pij на этот вектор:

F=Pn= напряжение вдоль направления вектора n.

Эта операция «смешивает» вклады от всех трёх базисных векторов тензора, учитывая ориентацию площадки.

Например, пусть нормаль к площадке направлена вдоль оси X:

n= (1; 0; 0). Тогда мы получим просто первый вектор тензора. Если же n повёрнут под углом, в формуле появятся комбинации всех компонент Pij. Таким образом, тензор позволяет «пересчитать» напряжения для любой ориентации, используя всего три базисных вектора.

Представьте, что три базисных вектора тензора – это основные цвета (RGB). Любой оттенок (направление) можно получить их смешением. Тензор – это инструкция, как комбинировать «цвета» -напряжения для получения «оттенка» -напряжения в произвольном направлении. Если бы у нас не было тензора, пришлось бы измерять напряжения для всех возможных углов, что физически невозможно. Тензор даёт компактную формулу вместо бесконечного числа экспериментов.

Почему в тензоре только три вектора, а не больше? Дело в том, что трёхмерное пространство описывается тремя независимыми направлениями (осями X, Y, Z).

Любой вектор или тензор в этом пространстве можно разложить по этим базисным направлениям. Добавление четвёртого вектора избыточно – он будет выражаться через существующие три. К примеру в механике если вы знаете силы, действующие на три взаимно перпендикулярные грани кубика, вы можете найти силу на любой наклонной грани через проекции. Дополнительные измерения не нужны.

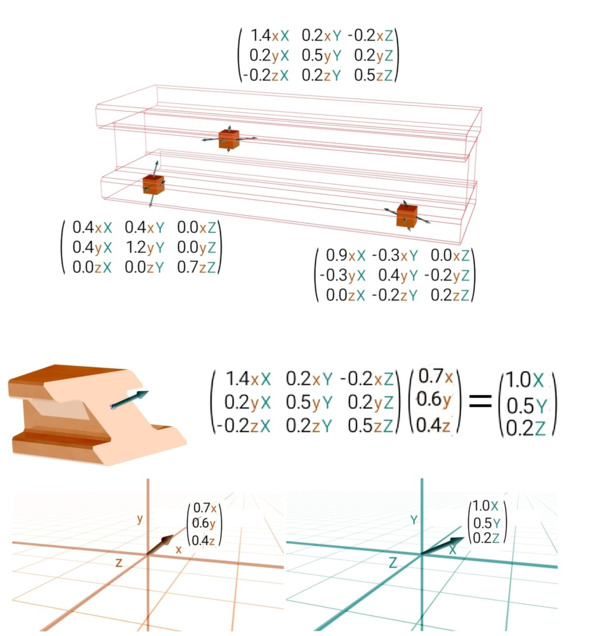
В разных точках балки могут быть разные напряжения, что порождает целое поле тензора, зависящего от координат. Пронзая его векторами, мы получаем значения сил.

Тензор напряжений, несомненно, олицетворяет и чисто физические законы. Симметрия тензора (Pij=Pji) – прямое следствие третьего закона Ньютона (действие равно противодействию) и сохранения момента импульса. Если касательное напряжение на

верхней грани толкает кубик вправо, то напряжение на правой грани должно толкать его вверх с той же силой. Если бы не симметрия соответствующих компонент, возник бы «неуравновешенный» крутящий момент, и кубик начал бы вращаться сам по себе, что противоречит реальности.

Тензор напряжений Pij в трёхмерном случае имеет 9 компонент, но из-за симметрии независимых только 6. Диагональные компоненты P11, P22, P33 представляют из себя нормальные напряжения, действующие перпендикулярно граням кубика.

Если P11=Pxx> 0 положительно, то это говорит о растяжении вдоль оси X. Если же эта компонента отрицательна, то происходит сжатие. Недиагональные компоненты P12, P23, …, представляют собой касательные (сдвиговые) напряжения, действующие вдоль граней. Например, Pxy – напряжение вдоль оси Y на грани, перпендикулярной X.

Существуют так называемые главные напряжения – это максимальные нормальные

напряжения, действующие в направлениях, где касательные напряжения равны нулю. Инварианты тензора напряжений используются в критериях прочности материала, например, в критерии Мизеса. Критерий Мизеса – это «правило», которое определяет, когда материал переходит в состояние пластической деформации (например, начинает течь, как пластилин) под действием сложных напряжений. Он отвечает на

вопрос: «При каком сочетании напряжений материал сдастся?». В основе критерия лежит идея, что пластичность зависит не от конкретных направлений, а от интенсивности касательных напряжений в материале. Для этого и используется тензор напряжений, а точнее – его инварианты.

Инварианты тензора напряжений – это величины, которые остаются неизменными при повороте системы координат. Они отражают фундаментальные аспекты напряжённого состояния материала, не зависящие от того, под каким углом мы на него смотрим. Вот их механическая интерпретация.

Первый инвариант I1 – «шаровая часть». Он олицетворяет среднее нормальное напряжение, действующее на материал, и гидростатическое воздействие. Если I1> 0 – материал сжимается равномерно со всех сторон (как под водой), если I1 <0 – растягивается. Таким образом, I1 отвечает за изменение объёма материала, но не влияет на его пластическую деформацию.

Второй инвариант I2 – «интенсивность искажения». Его физический смысл прост. Он характеризует интенсивность изменения формы материала (девиаторную часть), вызванную разницей между нормальными и касательными напряжениями.

Третий инвариант I3 – «сложность напряжённого состояния». Он отражает степень асимметрии в распределении напряжений.

Если I3 = 0, напряжения симметричны (например, при чистом сдвиге). Если I3 не ноль, то есть комбинация разнотипных напряжений (растяжение + сдвиг + кручение).

Видите, как массу всего полезного может сказать нам тензор напряжений? Если его пронизывать единичными векторами в разных направлениях (умножая его на них), он выдаст напряжение в этом направлении. Его же инварианты расскажут о среднем состоянии материала, причём выдадут три разных полезных характеристики!

Подытожим. Мы столкнулись с ситуацией, в которой одного вектора было мало для описания всех перекосов и растяжений вместе взятых. Но так как трёхмерное пространство – штука тесная, для описания всевозможных напряжений в нём нам хватило введения всего трёх векторов. Эти вектора оказалось возможным упорядочить и объединить в единое целое, записав в виде матрицы. А дальше уже сама математика дала нам возможность извлечь из этой конструкции максимум возможной информации.

Тензор возникает там, где одного вектора мало. Не хватает одного вектора – возьми больше! Что может быть проще?

Тензоры наглядно

В этом разделе мы, опираясь на уже имеющийся опыт работы с тензором, обобщим это понятие и сделаем применимым во всех подобных случаях. Мы научимся изображать тензоры так же наглядно, как вектора, и осмыслим операции над ними столь же естественно, как это делали раньше.

Как понять, что перед вами тензор?

Вектора нам знакомы уже давно и весьма интуитивны. Как только вы видите что-то, что имеет направление, вы можете описать это вектором. Но как понять, что перед вами более сложный объект? С механическим напряжением нам пришлось повозиться. Возникает вопрос: «Есть ли более простые критерии, говорящие о том, что мы имеем дело с тензором? Чтобы так же, как и с векторами, было всё легко и сразу понятно».

Да. Понять, что перед вами тензор, очень легко! Нужно вспомнить, что он является оператором-превращателем. Он берёт один вектор и превращает его в другой, имеющий, возможно, иное направление.

Давайте обратимся к физике и посмотрим, какие в ней есть подобные величины. Если мы вспомним о векторе импульса и о том, что он равен скорости, умноженной на массу (и иногда на релятивистский коэффициент), то поймём, что масса – это просто число. Коэффициент пропорциональности, если угодно., потому как вектор импульса и скорости всегда сонаправлены.

Теперь представим себе спутник, летающий где-то в небесах. Его скорость и импульс так же всегда сонаправлены. Но у вращающегося тела помимо импульса есть ещё и момент импульса. Он равен моменту инерции, умноженному на угловую скорость вращения. Спутник мы можем вращать вокруг разных осей. А значит, момент инерции относительно этих осей будет разным. Поэтому даже если спутник вращается с одинаковой по модулю угловой скоростью в обоих направлениях, из-за разной величины момента инерции его угловой момент будет разным. В одном случае он будет больше, в другом меньше. А значит, если сложить их вместе, получится, что результирующий угловой момент не совпадает по направлению с вектором угловой скорости. Это значит, что момент инерции это не число, а такой же превращатель одних векторов в другие – тензор!

Момент инерции и проводимость – тензоры.

Признаки видны сразу!

Теперь вспомним закон Ома в векторной форме. Вместо тока I у нас там вектор плотности тока J. Вместо напряжения U у нас вектор напряжённости Е. В самых простых случаях эти два вектора пропорциональны друг другу, и коэффициент пропорциональности именуется проводимостью. Но если перед нами необычный кристалл, то пропорциональность этих векторов нарушается. Ведь в специальных анизотропных кристаллах проводимость может зависеть от направления! Тогда вектор тока и напряжённости уже не будут коллинеарны. В этом случае проводимость уже оказывается тензором.

Так что критерий оказался весьма прост. Видя некое линейное уравнение или закон, посмотрите на его правую и левую части и спросите себя, куда направлены вектора, находящиеся по обе стороны, и совпадают ли они в самом общем случае. Если всегда совпадают, значит, перед вами скалярная величина. Если есть ситуации, где коллинеарность нарушается, значит, перед вами тензор во всей красе и информативности. Тензоры в физике и математике возникают повсюду. Даже обычная деформация – и то тензор! Поэтому настало время сделать то, что так любят математики: абстрагироваться от объектов и описать их на абстрактном языке, алгебраическом и геометрическом наглядном.

Абстрагируемся и обобщаем

Окинув мысленным взором всё, что мы уже поняли, давайте поразмыслим, как всё это можно обобщить. Матрицу (оператор) мы составляли из трёх векторов, и она уже позволяла нам изменять входящие векторы, превращая их в другие, имеющие даже другое направление.

Значит, для описания тензора нам нужно три вектора. Но эти векторы должны быть упорядочены. Хорошо это или плохо? На первый взгляд это может смущать. Но если мы вспомним, что вектор можно представить тремя компонентами, которые суть просто упорядоченный же набор чисел, то сомнения отпадут. Три упорядоченных числа для вектора, три упорядоченных вектора для тензора. Что тут такого?

Глядя на эту иерархическую лестницу, возникает интересная мысль. А давайте упорядоченные числа называть тензором первого ранга, а упорядоченные векторы – тензорами второго ранга. Скаляры же тогда само собой просится назвать тензорами нолевого ранга. Ну и логично предположить, что упорядоченные наборы тензоров второго ранга можно называть тензорами уже следующего – третьего ранга.

Ещё один важный момент нужно учесть. Компоненты вектора могут меняться в зависимости от базиса, в котором он рассматривается. Компоненты тензора тоже. Значит, когда мы записываем тензор в виде массива чисел, нужно учитывать, в каком базисе мы рассматриваем этот объект.

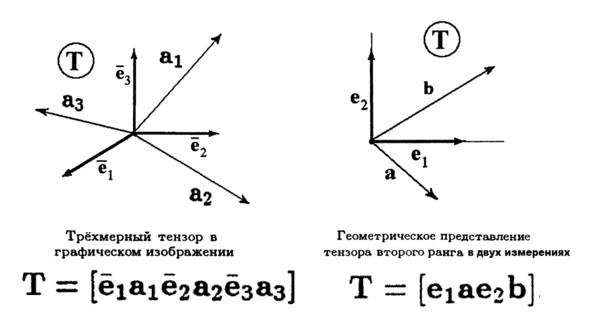
Наконец-то! Мы изобразили тензор!

Всё это подводит нас к вполне естественному геометрическому изображению тензоров. Будем называть тензором упорядоченную тройку векторов в некотором базисе. При этом сам рассматриваемый базис тоже упоминать графически и алгебраически. Алгебраически это тоже можно записать в виде набора из упорядоченных базисных и обычных векторов.

Будем называть данные вектора индивидуальными для тензора. Какую они имеют природу? Такую же, как и любой иной объект, имеющий направление и рассмотренный нами ранее. Каждый из индивидуальных векторов тензора может иметь ковариантные и контравариантные проекции на базисные векторы. Будем такие компоненты называть соответственно ковариантными и контравариантными. Но в отличие от вектора, тензор имеет больше свободы, и его можно представить в виде компонент смешанного типа! Один раз ковариантными и один раз контравариантными. Индексов-то два. Значит, один может быть верхним, другой нижним. Могут оба индекса быть внизу или оба наверху. Что в данном случае будет означать, например, двойная ковариантность тензора? Тут всё просто! Если мы базисный вектор увеличим в размере в 2 раза, ковариантные компоненты умножатся на 4. Контравариантные компоненты при аналогичном преобразовании уменьшатся в 4 раза. Если же тензор представлен компонентами один раз ковариантными, один раз контравариантными, то множители в виде 2 и 1/2 скомпенсируют друг друга, и компоненты не изменятся.

Но чтобы более детально говорить о преобразовании компонент, нужно чуть развить наш геометрический формализм. Научиться складывать наши тензоры подобно векторам, умножать на число и разработать иные операции над ними.

Операции над тензорами

Для простоты будем пока работать с тензорами второго ранга в двухмерном пространстве. Там у них будет всего два индивидуальных вектора, и будет очень наглядно видно, что меняется при применении той или иной операции.

Итак, вспомним, что мы умеем делать с векторами? Мы можем их складывать, умножать на число, скалярно умножать друг на друга, проецировать на базисные вектора. Вполне естественно переосмыслить те же самые операции применительно и к тензорам. Нужно только помнить, что тензор – это не число, это нечто ближе к матрице. И, соответственно, имеет значение, с какой стороны мы к нему подходим, особенно в вопросах умножения. Можно ввести скалярное умножение справа и слева, и они будут отличаться!

Также стоит вспомнить, что скалярное умножение по своей сути – это проекция, или, как её ещё называют, свёртка. Два вектора проецируются друг на друга, и проекция возрастает пропорционально партнёру. Это можно мыслить как взаимодействие вектора и дуального ему ковектора, компоненты которых суммируются (сворачиваются) по верхнему и нижнему индексу и дают число. Но у тензоров второго ранга индексов два! Соответственно, их можно сворачивать (скалярно умножать) с двумя векторами или сворачивать с таким же тензором. Что ж. Учтём и этот факт тоже.

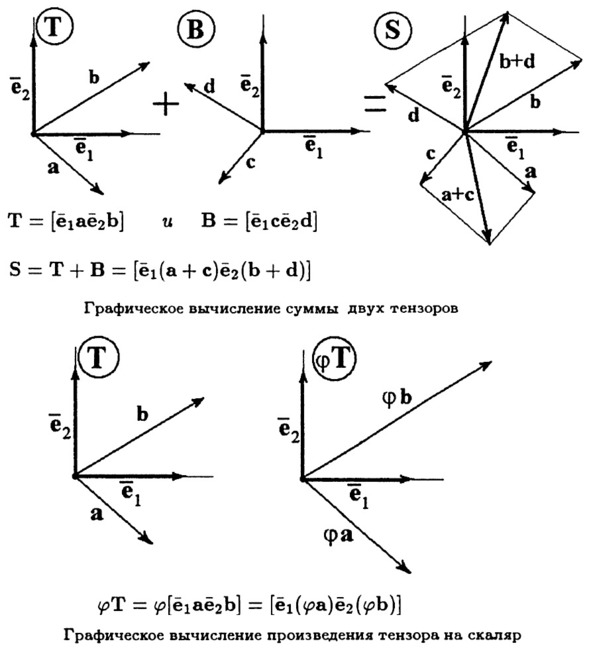
Складывать тензоры и умножать на число совсем просто.

С остальными операциями вопросов быть не должно. Вы наверняка уже сами догадались, как будет выглядеть, например, сложение. Есть, допустим, у нас два тензора T и B. У каждого из них есть свои индивидуальные вектора, имеющие притом свой порядок. Вполне логично под сложением понимать именно сумму векторов, стоящих на соответствующих по порядку местах! Новый тензор S, у которого индивидуальные векторы равны упорядоченной сумме индивидуальных векторов T и B, и будет результатом сложения.

Умножения тензора на число – тоже самоочевидно. Вполне логично удлинить все индивидуальные векторы на этот множитель.

Остальные операции рассмотрим подробнее.

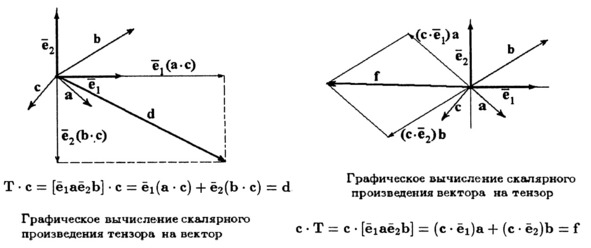
Скалярное умножение тензора на вектор слева и справа.

Если мы тензор умножаем на вектор скалярно, то тензор пишем слева, а вектор справа. В результате получим вектор, который является суммой базисных, умноженных предварительно на скалярное произведение индивидуальных векторов с тем, на который умножается тензор.

Если же мы вектор умножаем на тензор скалярно, то пишем уже его справа, а тензор слева. В результате получаем тоже вектор, но он представляет собой сумму индивидуальных векторов, масштабированных скалярным произведением базисных векторов на умножаемый вектор.

Скалярное произведение двух тензоров второго ранга даёт тензор второго ранга. Но его индивидуальные вектора представляют собой комбинацию в виде суммы индивидуальных векторов второго множителя, умноженных предварительно на скалярное произведение индивидуальных векторов первого множителя с базисными векторами.

Компоненты тензора совпадают с соответствующими компонентами его индивидуальных векторов!

Двойное скалярное произведение тензоров даёт уже число, являющееся суммой скалярных произведений индивидуальных векторов обоих тензоров.

Скалярное произведение, таким образом, и тут играет роль проекции, по крайней мере части элементов тензора на внешний объект. Соответственно, если мы тензор умножим и слева, и справа на базисные вектора скалярно, то получим его компоненты в этом базисе. Компоненты тензора тогда совпадут с соответствующими компонентами его индивидуальных векторов, что и должно быть! Значит мы всё сделали как надо!

Тензор второго ранга можно разложить по своему специфическому тензорному базису. Всё как и с векторами! Если мы хотим получить базисные тензоры, нам нужно рассмотреть такие объекты, в которых индивидуальные вектора как раз совпадают с базисными векторами. Логично! Ведь именно по базисным векторам разлагаются индивидуальные векторы.

Таким образом, все введённые нами операции вполне естественны и физически оправданы. Например, скалярное умножение тензора на число отражает изменение интенсивности

физической величины без изменения её направления или природы. Например, тензор напряжений в материале, умноженный на скаляр, соответствует увеличению или уменьшению нагрузки в системе. Такое масштабирование сохраняет линейность физических законов (например, закон Гука) и позволяет адаптировать модели к разным условиям (смена единиц измерения, переход к безразмерным величинам).

Тензоры умножаются скалярно несколькими способами.

Умножения тензора на вектор слева и справа часто описывают преобразование векторов в физических системах. Например, как мы видели ранее, умножение тензора напряжений на вектор нормали к поверхности (стоящий справа) даёт вектор силы, действующей на эту поверхность, что используется в механике сплошных сред. В анизотропных диэлектриках умножение вектора электрического поля на тензор диэлектрической проницаемости (вектор слева) позволяет вычислить электрическое смещение. Эти операции физически интерпретируются как проекции тензора на определённые направления или преобразование входных векторов в выходные (например, деформация под нагрузкой).

Двойное скалярное произведение (свёртка) двух тензоров уменьшает их ранг и суммирует взаимодействия компонент. Это ключевая операция для описания энергетических процессов. К примеру, свёртка тензора напряжений и тензора деформации даёт плотность энергии деформации.

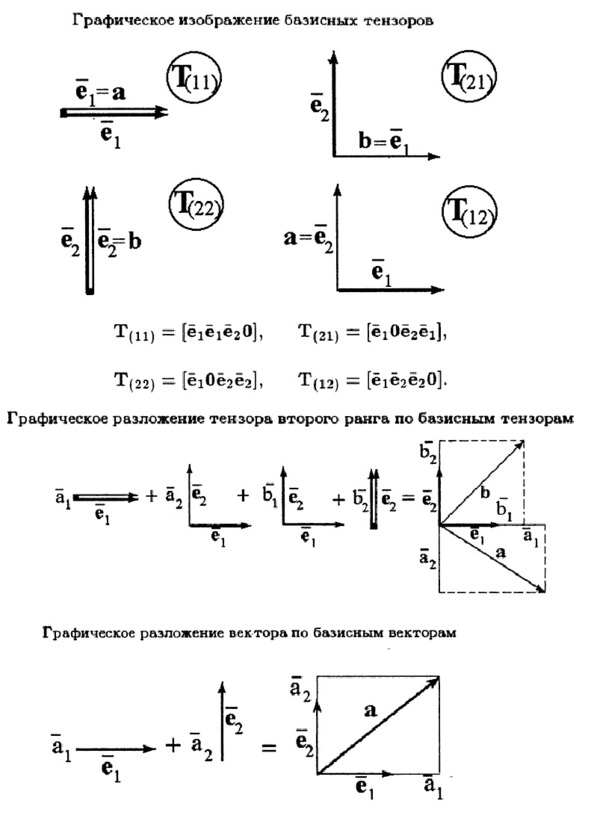
Тензоры можно разложить по тензорному базису

как векторы по векторному.

Все эти операции инвариантны относительно преобразований координат, что соответствует требованию ковариантности физических законов. Они позволяют компактно выражать сложные взаимодействия (например, анизотропные свойства материалов) и обеспечивают связь между математическим формализмом и наблюдаемыми величинами (силы, энергии, потоки). Без таких операций моделирование многомерных физических систем (деформируемых тел, полей в пространстве-времени) было бы невозможно.

Разложение тензора по базисным тензорам в физическом контексте соответствует выделению независимых компонент сложной величины, что позволяет анализировать её структуру, взаимодействия и симметрию. Эта операция аналогична разложению вектора на оси координат, но в многомерном и анизотропном случае.

В трёх измерениях и размерностях выше

все операции выглядят также.

Тензоры часто описывают сложные многокомпонентные взаимодействия. Разложение на базисные тензоры помогает разделить их на независимые части, каждая из которых соответствует определённому физическому эффекту. Вспомним пример из механики сплошных сред. В ней часто работают с уже знакомым нам тензором напряжений. Его можно разложить на шаровую часть (след тензора) и девиатор (безследовая часть). Шаровая часть соответствует гидростатическому давлению (объёмной деформации). Девиатор описывает сдвиговые деформации, вызывающие изменение формы. Это разделение критично для анализа пластичности материалов или разрушения.

Немного классификации

Когда мы говорим о векторах, у нас уже возникает некоторое их разнообразие. Мы можем говорить как минимум об обычной стрелке, единичном векторе, обратном или противоположно направленном векторе, аксиальном векторе (псевдовекторе), оборачивающемся в зеркале в свою противоположность и часто являющемся продуктом векторного произведения. От тензоров, в силу их более сложной структуры, следует ожидать ещё большего разнообразия их типов и разновидностей.

Начнём знакомиться с тензорным зоопарком с самого простого примера.

Нолевой тензор – это просто тензор в любом базисе, имеющий нолевые компоненты. Его индивидуальные вектора нолевые. Он является нейтральным элементом в случае сложения тензоров. Его прибавление ничего не меняет.

Если в качестве индивидуальных векторов тензора выбрать векторы базиса, то мы получим единичный тензор. Графическое его изображение будет выглядеть как совокупность двух «двойных стрелок». Примечателен он тем, что скалярное умножение единичного тензора на вектор что слева, что справа даёт тот же вектор. А скалярное умножение единичного тензора на другой тензор совершенно не меняет этот самый другой тензор. То есть он ведёт себя как обычная единица, только в мире векторов и тензоров.