Тензоры. Что может быть проще?

А что происходит в точке пересечения двух прямых? Там есть особенность – точка пересечения – это так называемый «разрыв» в структуре. Вокруг этой точки кажется, что пространство «ломается» – оно не выглядит как евклидово в окрестности этой точки, потому что вместо одной гладкой поверхности у нас тут «разрыв» или «узел». Там локально пространство не похоже ни на плоское, а скорее на нечто вроде «разреза», что ломает условие локальной евклидовости.

Покоряем непрерывность

Мы уже осознали проблему: каким бы ни было причудливым пространство, с которым можно столкнуться, изучая окружающий мир, нам придётся рассматривать его в малой окрестности и делать вид, что там оно почти плоское. Если совсем дела плохи, то – в бесконечно малой окрестности каждой точки. А значит, нам нужно вспомнить исчисление бесконечно малых, которое было переосмыслено и сейчас преобразилось в совершенно другую дисциплину – математический анализ. Да-да, те самые производные и интегралы. Возможно, и они на наш взгляд покажутся невероятно простыми и естественными.

Если кратко – то производная это мгновенная скорость изменения чего-либо. Именно её показывает спидометр автомобиля. Если величина меняется непрерывно, то для её исследования приходится довольствоваться именно мгновенным описанием. Ибо в следующее мгновение всё меняется, порой кардинально. К мгновенному описанию можно прийти через пределы, как это делают сегодня, или через отношения бесконечно малых величин, как это делали основатели данного исчисления. Бесконечно малое число – это следующее число после ноля. Вы его никогда не запишите численно, но оно ведь есть!

Сам Готфрид Лейбниц рассматривал кривые линии как ломаные, состоящие из бесконечно малых прямых отрезков. Так было их проще описывать. Эти бесконечно малые величины Лейбниц называл дифференциалами и обозначал как dx и dy, подразумевая под ними бесконечно малые приращения соответствующих переменных. Само понятие функции на тот момент было развито слабо. Речь шла об установлении зависимостей между разными величинами при их почти мгновенных приращениях, которые в конце можно было и отбросить. Идея великолепная и естественная! Но возникала проблема. Можно ли считать дифференциалы переменными? Современники Ньютона и Лейбница ухищрялись решать задачи, выбирая конкретные дифференциалы переменными, а другие меняли. Это превратилось в целое искусство. Кстати, Исаак Ньютон использовал другие обозначения. У него производная называлась флюксией (обозначалась точкой сверху), а аналог дифференциала моментом. Функция была потоком величины – флюентой. Знак интеграла у Ньютона – это просто квадрат, который он пишет перед выражением или просто обводит им интегрируемую величину.

Обозначения Лейбница прижились больше в силу большего удобства. Однако в современной математике потеряли первоначальный смысл. Знак интеграла в виде стилизованной буквы S Лейбниц ввёл позже. Изначально он писал I, а ещё раньше omn от латинского «omnis», что означает «весь» или «всё». Знак дифференциала d происходит от слова от латинского «differentia» – «разность» или «различие» Он мыслил знаки интеграла и дифференциала как операторы, которые взаимно уничтожают друг друга. В связи с чем, его доказательство основной теоремы анализа (формулы Ньютона-Лейбница) выглядит невероятно простым, до наивности.

Что изменилось впоследствии? После работ Огюстена Коши, Карла Вейерштрасса и других учёных исчисление преобразилось до неузнаваемости и перестало быть противоречивым.

Вся суть матанализа в нескольких графиках!

Под интегралом сегодня понимается предел суммы. Под производной – угловой коэффициент касательной. Дифференциал же вообще перестал быть бесконечно малой величиной. Теперь это приращение ординаты y касательной при приращении аргумента x, и эта величина может быть любого размера. Если удобно, её всё ещё можно мыслить и как бесконечно малую. Работать уравнения будут всё равно одинаково.

А раз работать будет, то нам всё-таки проще мыслить все эти величины как их основатели. Это привнесёт большую наглядность в наши исследования.

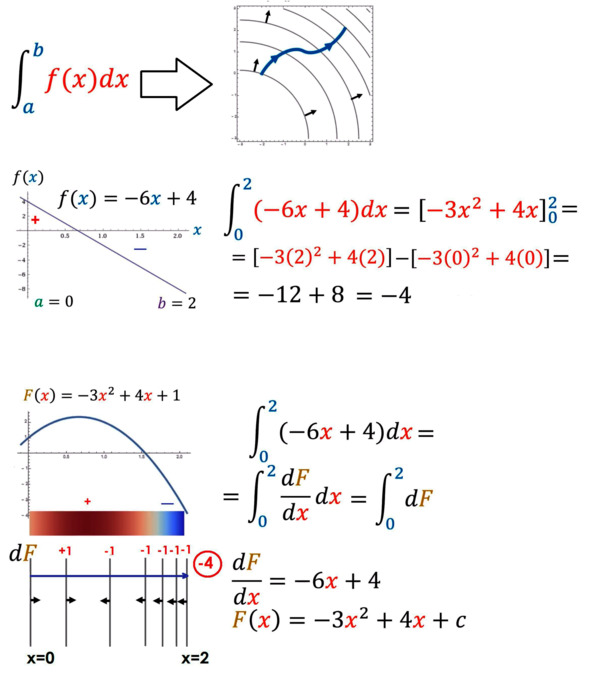
Бросив взгляд на историю становления матанализа, давайте пробежимся по основным его столпам. Чтобы получить производную функции, мы рассматриваем отношение разницы значения функции и значения аргумента в окрестности какой-то точки. Это отношение равно тангенсу наклона секущей, проведённой через данные точки. Если мы уменьшаем приращение аргумента до ноля, то секущая вырождается в касательную. Тангенс касательной – наилучшее приближение для мгновенной скорости! И он-то как раз и будет равен отношению того, что называют дифференциалами – приращение ординаты касательной к её аргументу! Всё сошлось!

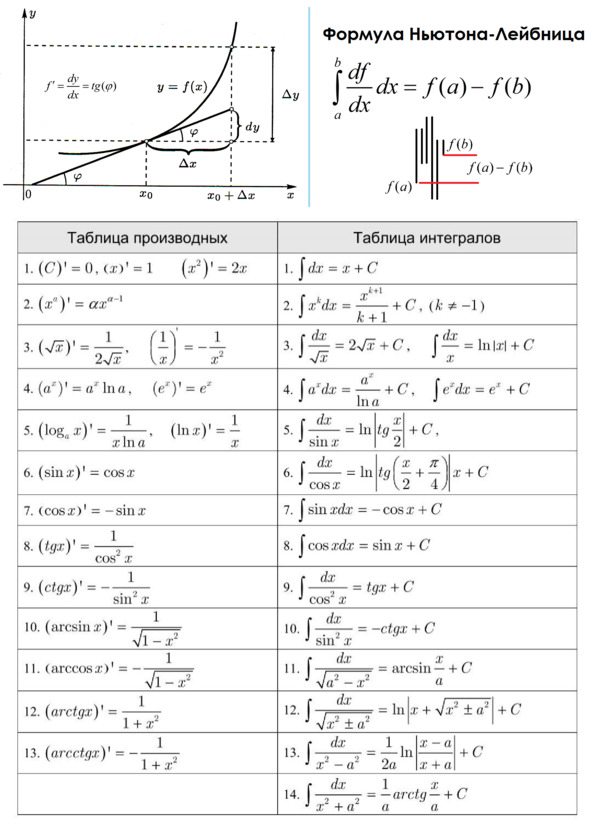
Пригодится помнить!

Алгебраически тоже всё просто. Мы прибавляем к аргументу функции бесконечно малую величину, вычитаем из неё неизменённую функцию и делим на бесконечно малую как на число. После алгебраических преобразований получаем удобный ответ, в котором полагаем бесконечно малую равной нолю (устремляем к нолю).

Интегрирование возникает, если мы пытаемся вычислить площадь под кривой функцией. Под прямыми линиями нам хватило бы обычной геометрии. А тут нам приходится разбивать пространство под изогнутой непрерывно фигурой на маленькие участочки, в каждом из этих интервалов рассматривать узкие прямоугольнички и делать их бесконечно малыми. В пределе мы получим интеграл – площадь под кривым графиком.

Как увидеть, что интегрирование и дифференцирование являются взаимно обратными операциями? Для этого достаточно всего лишь рассмотреть площадь под графиком как функцию аргумента. Чем больший аргумент мы берём, тем больше площадь. Что будет являться дифференциалом такой функции? Разумеется, бесконечно малый прямоугольничек, вычисляемый как значение функции, умноженное на бесконечно малое приращение dx. Если разделить выражение для дифференциала площади на это приращение, мы получим, что производная площади – это как раз наша функция! Всё, связь установлена.

Так легко прийти к формуле Ньютона-Лейбница. Но не позволяйте этому стать для вас просто формулой. Всмотритесь вглубь. Как её можно понять на пальцах? Под интегралом стоит производная функции, умноженная на dx. Значит, на деле мы имеем просто сумму изменений функции. Шаг вверх, потом вниз, потом опять вверх и так далее. Топчась вверх и вниз, в итоге где мы окажемся? Каково расстояние между точкой старта и точкой финиша? Конечно же, разность значений функции в этих точках, всё остальное скомпенсировалось и вычлось! Это же так просто и очевидно!

Обстановка в кривом пространстве

Многообразие – это, по сути, искривлённое пространство, которое выглядит плоским в небольшой локальной области. Самый известный пример многообразия – поверхность Земли. Недаром её тысячелетия считали плоской! На большом расстоянии поверхность земли представляет собой сферу геоид. Но для нас, наблюдателей, живущих на поверхности, земля выглядит плоской в небольшой локальной области. Это позволило Евклиду построить именно плоскую геометрию имени себя, а не риманову. Помимо сфер, к наиболее знакомым примерам многообразий относятся цилиндры, бублики, седловидные поверхности, лента Мёбиуса и бутылка Клейна. Кстати, бутылка Клейна – это результат склеивания двух лент Мёбиуса. Их невозможно соединить полностью в трёхмерном пространстве, но если выйти в четвёртое измерение и проедать это, получим бутылку Клейна. Существуют также многообразия с краем (типа диска). И неориентируемые многообразия, примером которой и является уже упомянутая лента Мёбиуса, обладающая всего лишь одной стороной. Если в многообразии есть понятие расстояния между двумя точками, мы называем его римановым многообразием. Но давайте задумаемся, как вообще можно измерять расстояния? В плоскости мы можем это делать с помощью метрического тензора. Помещаем в него вектор, соединяющий точки, два раза, на выходе получаем квадрат длины. А как научиться делать это в кривом пространстве? Да и как вообще в подобной структуре дела обстоят с векторами? Векторы – это стрелки. Разве не будут они торчать ёжиком в случае кривого многообразия? Или нам стоит их тоже изгибать, как и само пространство? Как вообще математически описать линию в кривом пространстве? Давайте разбираться!

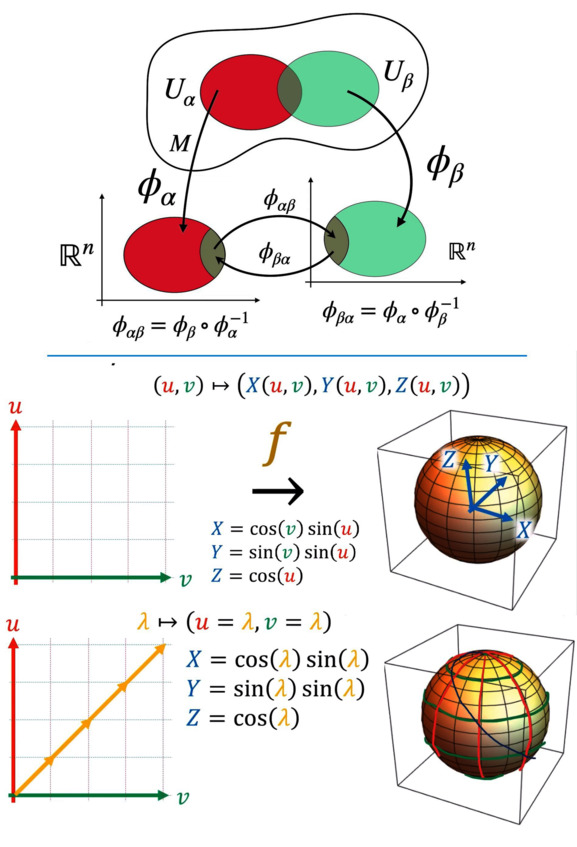
Отображение плоскости на поверхность. Видно, как ведёт себя линия из плоскости после проекции в кривом пространстве.

Для простоты рассмотрим двумерную кривую поверхность. Первый вопрос, который нужно задать. Как математически описать двумерную поверхность, помещённую в трёхмерное пространство? Карты и атласы – это да. Но в деталях, как это реализуется на практике? Ну, на практике самое простое – это взять двухмерную плоскость с координатами и предъявить какую-либо удобную функцию, которая растянет и преобразует плоскость, «накинув» её на двухмерную поверхность. По сути, мы берём каждую точку пространства и присваиваем ей координаты в трёхмерном пространстве.

Как нам нарисовать кривые на сфере? Или, в более общем случае, как перенести кривую из плоскости на нашу поверхность? Для этого мы берём уравнение пути и пропускаем его через функцию, отображающую плоскость в поверхность, и получаем результат – путь внутри поверхности! Если всё сделано правильно, то можно заметить, что путь пересекает координатную сетку на поверхности точно так же, как он это делал в плоскости.

Векторы внутри кривого пространства можно ввести, если вспомнить, что ими задаётся, например, скорость изменения параметра кривой. Всё как и с функцией. Берём два радиус-вектора, показывающих положение точки на кривой, принадлежащей поверхности. Устремляем разницу между ними к нолю. Вектор смещения точки, который, вообще говоря, может прокалывать саму поверхность, превращается в стрелку, касательную к кривой.

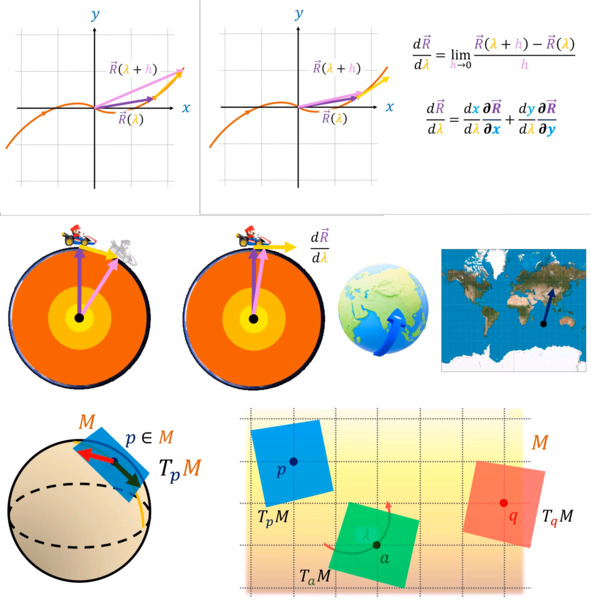
Каждая точка многообразия имеет касательное пространство, в котором живут векторы.

Мы и так уже морально готовы к тому, что в кривых пространствах будем работать с локальными картами, эмитирующими евклидову геометрию. Поэтому, слегка поразмыслив, так же поймём и смиренно примем, что вектора можно относить лишь к каждой точке многообразия отдельно. В одной точке мы имеем всевозможные вектора, которые могут смотреть по касательной в противоположных направлениях. В другой точке будет другое касательное направление. Значит, имеет смысл говорить, что вектора на многообразиях живут лишь в касательных пространствах, которые имеются в каждой их точке. Множество всех касательных пространств данного многообразия называют касательным расслоением. Ковекторы тоже живут в касательном пространстве, иначе они бы не могли есть вектора, выдавая число. Такое множество касательных пространств для ковекторов называют кокасательным расслоением.

Раз мы поняли, где живут векторы и ковекторы, то и тензоры построить совсем просто. Тензоры типа (r;s) на гладком многообразии M живут в тензорных расслоениях типа (r;s), обозначаемых как T (r;s) M. Эти расслоения строятся как тензорные произведения касательного TM и кокасательного TM∗ расслоений.

Векторы – новый облик

Многообразие можно изучать несколькими способами. Мы можем представить, что находимся снаружи и смотрим на него из пространства большего числа измерений. Так более наглядно, но не всегда бывает возможно реализовать. Можно смотреть на многообразие изнутри, например, как австралопитеки смотрели на поверхность земли, или мы смотрим на пространство-время вселенной.

И такой взгляд изнутри кривого пространства заставляет нас немного пересмотреть наши основные понятия. Да, локально у нас всё плоско. Но нам некуда тыкать векторами, ведь в окрестности соседней точки всё будет совсем иначе. Когда мы рисуем вектор на плоскости, он выглядит как стрелка с направлением и длиной. Но что происходит, если пространство искривлено? Например, поверхность сферы или холмистая местность. Здесь координатные оси могут изгибаться от точки к точке, и обычные стрелки теряют смысл. Нужен способ описывать направления и скорости, который работает в любой системе координат.

При переходе от одной системы координат к другой, в криволинейном случае, матрицы перехода для векторов состоят из частных производных и называются якобианами.

Представьте, что вы идёте по глобусу. Если в точке A вы нарисуете стрелку «на север», а в точке B – тоже «на север», эти стрелки не будут параллельны из-за кривизны Земли. В искривлённых пространствах нельзя просто «перенести» вектор из одной точки в другую. Координатные системы локальны и зависят от точки. Возникает закономерный вопрос: как определить вектор так, чтобы он не «ломался» при смене координат и работал на всём многообразии? Подумайте. Сопоставляйте всё, что вам известно уже о многообразиях, функциях и полях.

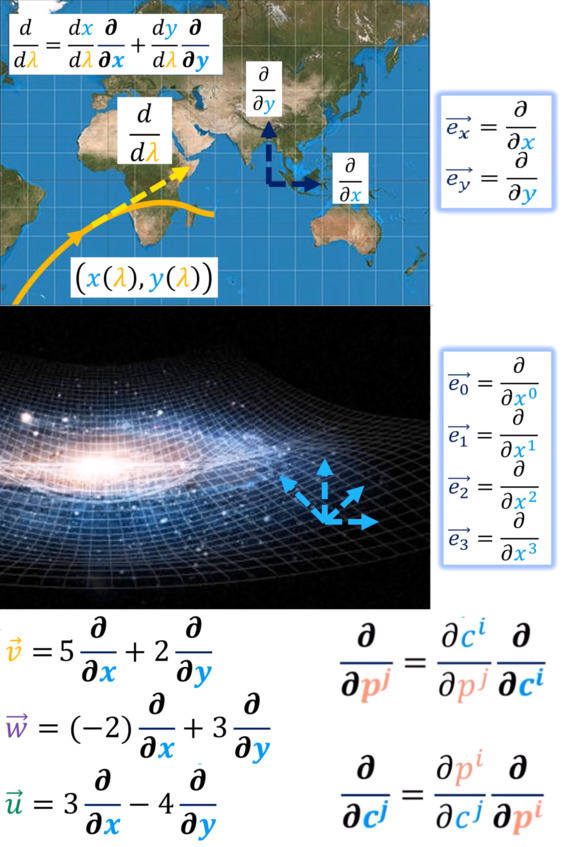
Векторы как операторы неизбежно возникают, если вы живёте внутри многообразия.

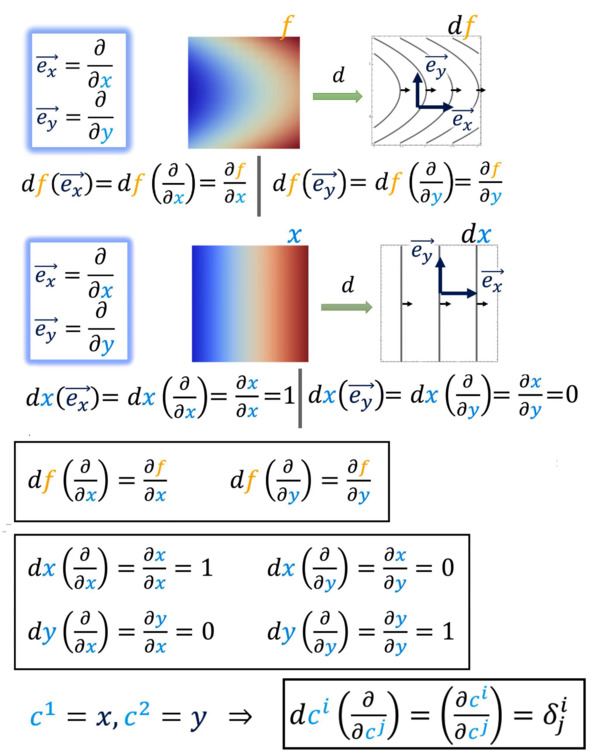
Ответ кроется в том, как векторы взаимодействуют с функциями. Пусть у нас есть некоторая гладкая функция f (например, температура) на многообразии. Вектор в точке p должен отвечать на вопрос: «С какой скоростью меняется f, если двигаться вдоль этого направления?» В математике это называется производной по направлению.

Чтобы описать производную по направлению, математики заметили, что вектор можно отождествить с дифференциальным оператором, который действует на функции. Операторы дифференцирования по координатам представляют из себя частные производные. Это когда мы всё, что не является данной координатой, считаем константой. Эти операторы можно складывать и умножать на числа, как и обычные вектора. А значит, они тоже образуют структуру некоего линейного векторного пространства. Более того, как и вектор, каждый такой оператор отвечает определённому заданному пространству! Математики в таком случае говорят, что существует изоморфизм между векторами и дифференциальными операторами. Это как бы структуры-двойники, имеющие идентичные свойства, хоть и разную на первый взгляд природу.

Да, замена векторов на какие-то там дифференциальные операторы выносит мозг. Но нам на этом этапе очень важно понять, что операторы – это не прихоть, а необходимость, неизбежность и сама суть понятия вектора на многообразии! Бонусов от этого откровения множество. Это и инвариантность, так как операторы работают в любых координатах. И гибкость. Ведь их можно комбинировать с функциями и друг с другом. И, конечно же, измеримость – они напрямую связаны с наблюдаемыми величинами (скорости, ускорения, потоки). Стрелки – это прекрасная иллюстрация, но на искривлённых пространствах они «ломаются» без операторной алгебры. Дифференциальные операторы – это «мозг» векторов, который считает, дифференцирует и адаптируется к любой геометрии.

Если бы Ньютон изучал многообразия, он бы сказал: «Векторы – это дифференциальные операторы, и точка».

Ковекторы – новый облик

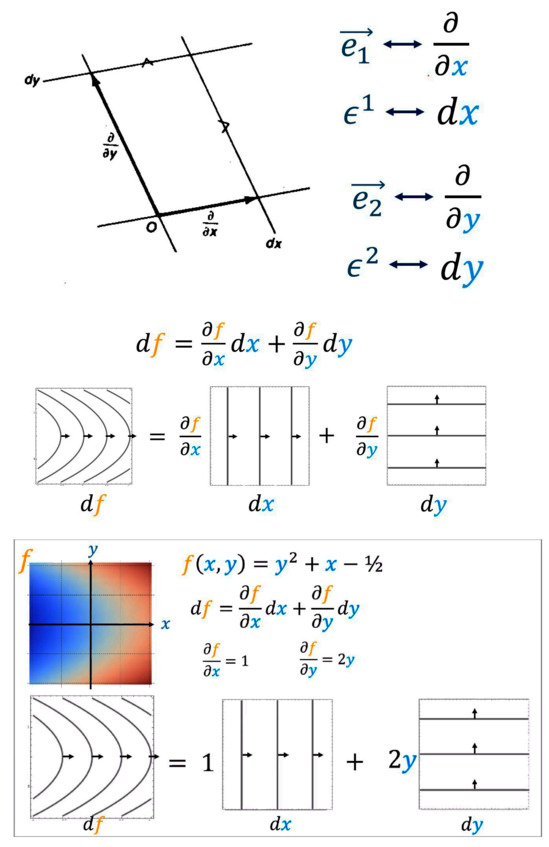
Вектора преподнесли нам сюрприз, оказавшись дифференциальными операторами. А как быть с ковекторами? Они ведь дуальны векторам, а значит, мы их можем встретить в уравнениях с частными производными для функции нескольких переменных. И действительно, после взгляда на такие уравнения нас осенит. Дифференциалы и ковекторные поля – это одно и то же! Давайте покрутим в голове этот факт и получше его осознаем.

Итак, вы помните, что дифференциалы – это небольшие изменения переменной, которые вы видите, например, под знаком интеграла. Взятие дифференциала – линейная операция. Обычно мы представляем, что символ дифференциала берёт переменную и даёт нам её бесконечно малое изменение. Но точно так же можно представить, что символ дифференциала берёт скалярное поле и выдаёт ковекторное поле! Поле – это когда в каждой точке пространства что-то задано (число, вектор, тензор) и может меняться от точки к точке. Скалярное поле – это пространство, где каждой точке соответствует скаляр. А ковекторное поле – это пространство, где каждой точке соответствует свой ковектор. Если у нас есть скалярное поле, то, как и раньше, мы можем построить ковекторное поле, задав кривые уровня данного скалярного поля. Кривые уровня – это кривые, на которых данная величина скалярного поля остаётся постоянной. Очень часто скалярные функции называют 0-формами, а их дифференциал – 1-формами.

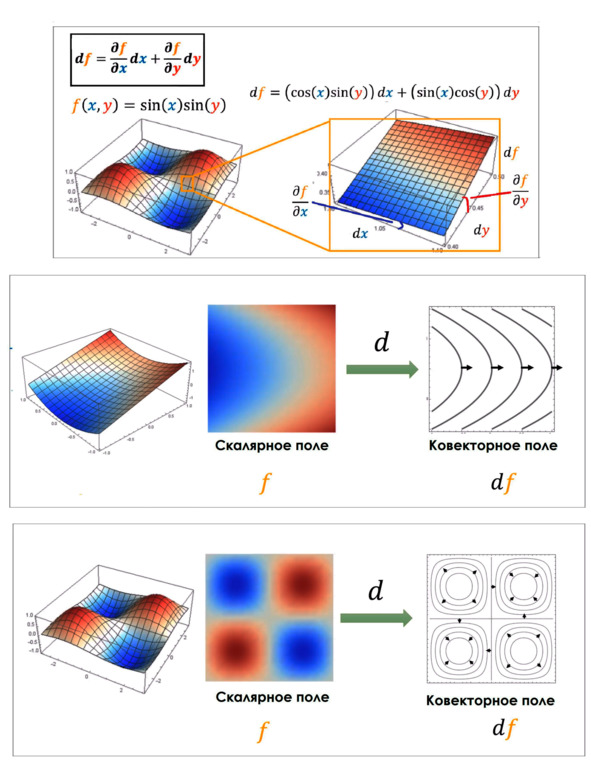
Дифференциал скалярного поля – это ковекторное поле!

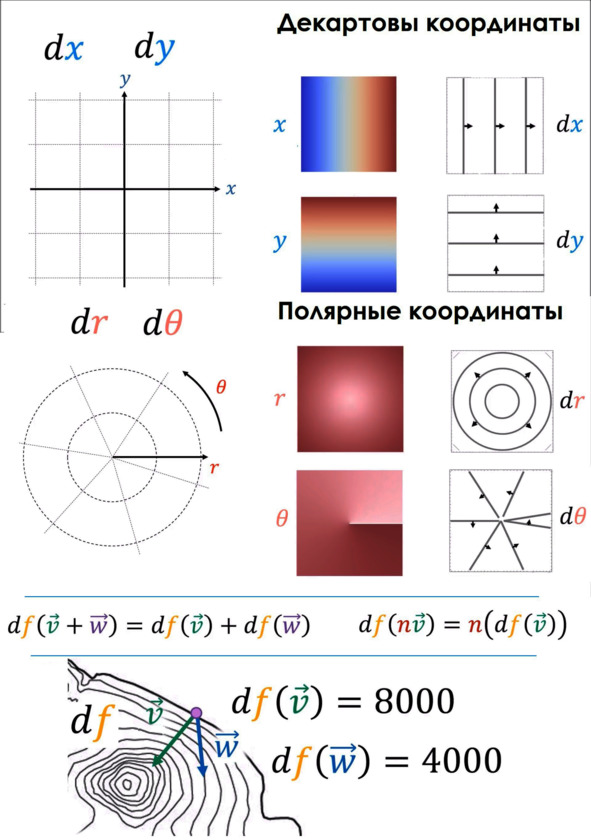
Мы можем в нашем расследовании пойти дальше и задуматься над тем, как будут выглядеть дифференциалы координат, если сами координаты представить в виде скалярного поля. И тут наше предположение окажется верным! Дифференциалы координат высветят нам линии постоянства той или иной координаты в точности как базисные ковекторы! Так же произойдёт в любой криволинейной системе координат. Только ковекторные поверхности будут смотреть в каждой точке в разных направлениях.

Воздействия ковекторов на векторы будет в точности таким же, как раньше. Единственное, что его теперь можно вычислять, только указывая, в какой конкретной точке это происходит. Иначе чуть сместишься, и поверхность ковектора там другая и иначе пересекает вектор.

Производная по направлению линейна, как и дифференциал.

Давайте повнимательнее посмотрим на геометрический смысл воздействия дифференциала функции (новый облик ковектора) на вектор (дифференциальный оператор, указывающий направление). Для этого достаточно вспомнить пример с горой, которую пытаются изобразить картографы. Векторы, направленные в разные стороны, будут указывать на направления, в которых будет разное количество линий уровня. Следовательно, числа при взаимодействии с данным ковектором даже из одной и той же точке они будут выдавать разные. Как результат мы получаем, что свёртка дифференциала и вектора пропорциональна крутизне возрастания функции в направлении этого вектора. Если вектор направлен вдоль более крутого склона, значение его взаимодействия с ковектором увеличивается. Это означает, что дифференциал функции как ковектор, будучи спроецирован на оператор дифференцирования, задающий направление, измеряет скорость изменения функции через точку со скоростью, заданной вектором-оператором. Получается, что данная конструкция является производной по направлению вектора от функции, дифференциал которой мы рассматриваем.

Удивляемся новым возможностям

Рассмотренный нами подход в переосмыслении векторов и ковекторов уже позволяет нам работать с многообразием без координат вообще! Сами линии ковекторов – это некий объект в себе. Направления векторов – тоже. Они могут взаимодействовать друг с другом без всяких там карт и координат! Но к этому стоит привыкнуть. Поэтому давайте ещё раз пройдёмся по более интуитивно понятным аналогиям. Уж больно специфическая тема.

Представьте, что вы путешествуете по холмистой местности. У вас есть компас, показывающий направление (это вектор), и топографическая карта с линиями уровня, обозначающими высоту (это ковектор). Вектор говорит: «Иди сюда», а ковектор показывает: «Как быстро изменится высота, если пойти туда». Их взаимодействие – это суть дифференциальной геометрии, где направления и измерения сливаются в единый язык.

Дуальность на месте!

Вектор на многообразии – это не просто стрелка. Это правило движения. Например, если вы стоите на склоне горы, вектор может означать: «Сделай маленький шаг вдоль тропы». Но чтобы понять, что происходит с миром вокруг при этом шаге, нужен ковектор. Вектор действует как дифференциальный оператор – он «берёт» функцию (например, высоту или температуру) и возвращает число: скорость её изменения вдоль выбранного направления. Если вектор – это шаг, то оператор – это ответ на вопрос: «На сколько изменится высота, если этот шаг сделать?».

Дифференциал можно также раскладывать по базису.

Ковектор – это дифференциал функции. Вернёмся к топографической карте: линии уровня высоты сгущаются на крутых склонах и редеют на равнинах. Ковектор кодирует эту информацию. Он не указывает направление, а измеряет, как функции реагируют на движение.

Если функция – это высота, то её ковектор – это набор линий, где каждая линия соответствует постоянному значению высоты. Чем ближе линии, тем «сильнее» ковектор – тем быстрее меняется высота при движении.

Если вы идёте вдоль вектора, который пересекает 5 линий уровня высоты за один шаг, то свёртка вектора и ковектора даст число «5» – скорость набора высоты. Если линии уровня далеко друг от друга, число будет меньше – склон пологий.

Свёртка вектора и ковектора – это производная функции вдоль направления вектора. Но вместо формул – визуальный счёт пересечений. Чем чаще вектор «натыкается» на линии уровня, тем быстрее растёт функция.

Всё наглядно и понятно!

Но самое интересное и неожиданное состоит в том, что даже интегрирование, которое мы всегда делали через координаты, мы теперь можем выполнять вообще без них!

Обычно интеграл требует задания координат: разбиваешь путь на кусочки, считаешь значения в точках… Но с ковекторами всё иначе. Если ковектор – это линии уровня, то интеграл вдоль пути – это просто «сколько всего линий пересекает путь»! Всего-то!

Смена координат происходит как положено!

Вот как это работает на практике. Выберите путь на многообразии (например, тропу через холмы). Пройдите по нему, считая, сколько раз путь пересекает линии уровня ковектора (например, линии высоты). Сумма пересечений – это и есть интеграл. Если вы поднимаетесь вверх, пересекая много линий, интеграл будет большим. Если идёте вдоль линии уровня – нолевым.

Вычислим интеграл двумя способами: через координаты и

как путь в ковектороном поле.

Замена координат никак не повлияет на значение интеграла. Главное – учитывать, в каком направлении мы пересекаем ковектор: в положительном для него или в отрицательном. Эти значения нужно суммировать с учётом знака.

В двухмерном пространстве результат один и тот же при подсчёте через координаты и без них.

Такой подход очень полюбился физикам. В механике работа силы вдоль пути – это интеграл ковектора (силы) по векторному полю (пути). Силу можно представить как линии потенциала: работа – это величина, показывающая, «сколько потенциала» потрачено на движение.

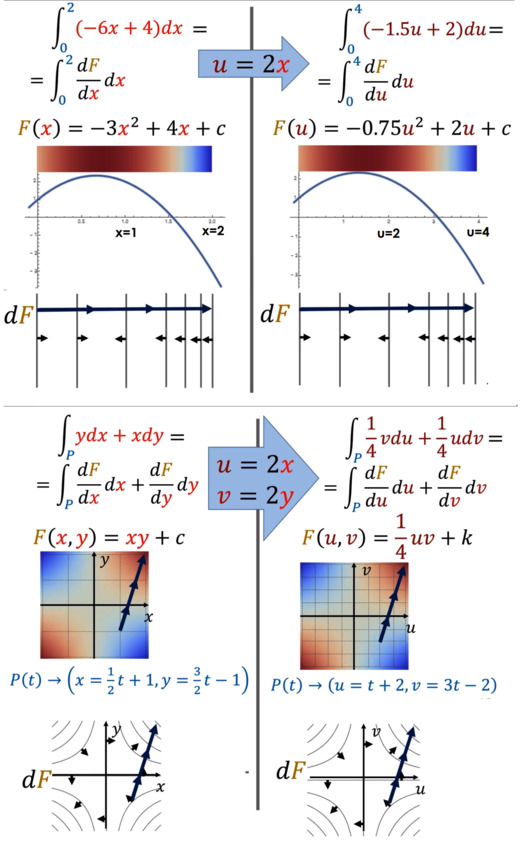
Ковекторы и путь – это геометрия! Они не зависят от координат.

Этот метод подсчёта интеграла совершенно не привязан к координатам! Представьте, что вы в джунглях без карты. Если вы знаете ковектор (например, градиент температуры), то можете чувствовать, как меняется температура при движении в любом направлении (свёртка с вектором). А также вы будете способны вычислить общее изменение температуры на маршруте (интеграл), даже не зная координат.

Ковекторы и векторы работают в любой системе координат, потому что они опираются на геометрию, а не на условные сетки. Линии уровня существуют независимо от того, как вы рисуете оси «x» и «y».

Векторы и ковекторы – простейшие примеры тензоров. Их свёртка – частный случай более общей идеи: тензоры измеряют, как геометрические объекты взаимодействуют в разных направлениях. Например, если ковектор – это линии уровня, то тензор типа (0;2) – это сетка из линий, измеряющая, как два вектора совместно влияют на функцию (как изгибается ландшафт). Свёртка таких тензоров с векторами даёт «проекции» их силы на многомерные линии уровня.