Формирование звёзд и планет с точки зрения школьной физики. Детальный алгоритм рождения звёзд и появления планет, и следствия из него

И более того, этот же алгоритм показывает, почему исходно некоторые снежинки могли вырасти до планетных размеров, находясь не строго в плоскости протопланетного диска, а пересекая его под достаточно большим углом – ныне для всех планет Солнечной системы он составляет около 7 градусов. Достаточно было зародышу одной планеты (Юпитера) родиться с большим углом наклона, например в результате очень быстрого слипания частиц в верхней точки траектории над экватором, после чего он набирал массу по своей траектории, почти не меняя угла наклона орбиты, и когда он стал самой большой планетой солнечной системы – постепенно стабилизировал траектории всех остальных планет относительно себя.

Глава 3.2 Появление у планет вращения вокруг своей оси, совпадающего с направлением вращения вокруг Солнца

Подготавливая статью о происхождении Солнца и планет к публикации, внезапно наткнулся в интернете на тот факт, что если верить книгам и СМИ, оказывается многим астрофизикам до сих пор не очень понятно каким именно образом у планет Солнечной системы образовалось вращение, совпадающее с направлением вращения самого Солнца и планет вокруг него. А ведь это, по сути, элементарная задачка по механике, для 10—11 класса. Здесь самое время с нею разобраться.

Итак, исходное пылевое облако сгустилось в отдельные снежки как минимум килотонного класса. Далее из них родятся планеты – но в какую сторону они будут вращаться?

Ещё Лапласа мучал вопрос – почему их направление вращения совпадает с направлением вращения вокруг Солнца, хотя вроде бы должно быть наоборот? Рассуждения были таковы. Исходно все зародыши вращаются по приблизительно круговым орбитам, и чем ближе к Солнцу – тем быстрее. Получается, что если взять группу близко расположенных снежков (например в радиусе 1000км от заданной точки), и посчитать их момент вращения как сумму моментов скоростей относительно центра масс выбранной группы – он будет явно противоположно направленным моменту вращения плоскости. Так в чём же ошибка?

Ошибка опять в том, что пытались посчитать момент вращения, забыв о гравитационном поле, притом неоднородном. Исправляю этот просчёт, показав всю логику на примере простой модели.

Сперва решим упрощённую задачу. Допустим у нас исходно есть всего 2 группы снежков, с одинаковым количеством элементов (например миллион) равной массы в каждой группе (М1 и М2), вращающихся вокруг Солнца по строго круговым орбитам (радиусами R1 V2). Между ними начинается длительное и очень сложное гравитационное взаимодействие, которое мы для простоты сведём к одному единственному краткому взаимодействию – в некоторый момент все снежки получили равные по модулю импульсы в сторону орбиты другой группы – то есть снежки нижней орбиты получили импульс от Солнца, а верхней орбиты соответственно к солнцу, после чего снова полетели по законам Кеплера. Тогда дальнейший их полёт пойдёт уже по эллипсам, снежки верхней группы немного опустятся, а нижние наоборот поднимутся. Теперь, зная это, выбираем начальный импульс взаимодействия таким, чтобы перигей орбиты верхних снежков по высоте совпал с апогеем нижних – на орбите радиуса R. И именно на этой орбите снежки должны будут попарно столкнуться. Вопрос, что мы увидим?

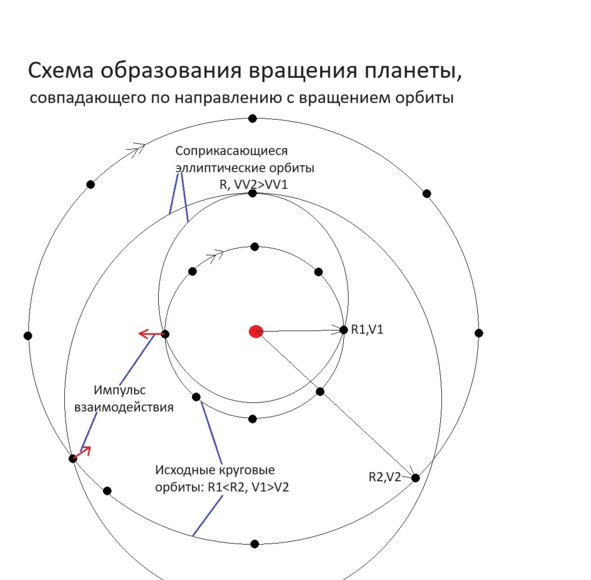
Для кругового движения по орбите R надо иметь некую круговую скорость V. Нижние снежки поднялись наверх, против гравитационного поля, погасили свою скорость, и в апогее имеют скорость VV1 V> VV1, так как после перигея должны вновь подняться вверх. Получается, что снежки, которые снизу, имеют скорость VV1

Теперь возвращаемся к исходной реальной задаче, в которой есть не две группы снежков на двух орбитах, а целый рой на всех возможных орбитах. Исходно, после фазы начальных массовых столкновений, снежки должны вращаться почти стационарно, по близким к круговым орбитам. Далее взаимодействуя случайным образом друг с другом, они начинают медленно изменять свои орбиты на эллиптические, до тех пор, пока орбиты наконец не сблизятся настолько, что летящие по ним снежки наконец не получат возможность войти в сферу ближнего притяжения друг с другом, с последующим столкновением. То есть, перед самым столкновением орбиты двух сталкивающихся снежков будут являться двумя едва касающимися друг друга эллипсами, орбита одного снежка будет в основном внутри орбиты другого. А раз так, то повторяя те же рассуждения, что и для круговых орбит упрощённой задачи, получаем, что в момент столкновения, скорость снежка с внешней, более высокой орбиты оказывается немного больше скорости снежка с внутренней низкой орбиты, и результат их столкновения имеет то же направление собственного вращения, что и направления вращения орбит обоих снежков вокруг Солнца.

Конечно, иногда будут происходить и столкновения снежков на сильно пересекающихся траекториях, и тогда будут не касания орбит, а именно их пересечения, и в результате слипания итоговый комок может получать самые неожиданные направления вращения. Например, мы забыли что движение снежков происходит в трёхмерном пространстве, а значит и результат столкновения будет трёхмерным телом, имеющим две степени свободы для момента вращения. Но в среднем, большинство столкновений будут происходить после длительных медленных взаимодействий, когда орбиты едва только успеют соприкоснуться. И таким образом, среднестатистически по мере столкновений, момент вращения образующейся протопланеты будет всё больше увеличиваться именно в нужную сторону. Ну а то, что оси вращения планет не идеально совпадают с осью вращения их орбит, связано именно с тем, что статистический метод работает только при столкновении огромного числа малых сгустков. А вот на последнем этапе, при столкновении уже реально больших планет типа Марса, для формирования Земли, очень важную роль уже играет случайность, и возможность планет лететь не строго в математической плоскости экватора – пролети одна из сталкивающихся планет тысячей километров выше или ниже экватора, и момент вращения результата столкновения может измениться очень сильно в любую сторону.

Глава 3.3 Когда и как сформировались планеты? И почему Солнце крутится так медленно? Теория каменного дождя

Зададимся таким вопросом – когда именно, то есть на какой стадии из газопылевого диска вокруг звезды успели сформироваться планеты? Кто же старше – Земля или Солнце? И почему планеты имеют столь разную плотность, а значит и разный химический состав, если все они сформированы из одного облака? И наконец – откуда в космосе могли взяться не просто ледяные или каменные метеориты, но так же и железо-никелевые, которые вроде бы должны были быть получены из центров столкнувшихся планет – чего никак не могло произойти, о чём говорят все результаты компьютерных моделирований столкновений.

Разумеется, если только планета не захвачена из иной звёздной системы, она младше протосолнца, ведь до его формирования в качестве центрального массивного элемента диска, не мог сформироваться и сам пылевой диск. Однако мы уже знаем, что как только протозвезда становится квазизвездой, она начинает очень интенсивно светить – нашему Солнцу понадобилось бы минимум 50млн лет, чтобы при нынешней светимости (3*10^26Вт, 10^34 Дж/год) высветить всю энергию гравитационного падения материала (это минимум 5*10^41Дж). А что если наша исходная квазизвезда была не тусклой долгоживущей туманностью, а наоборот достаточно яркой (что-то типа Бетельгейзе, которая светит как сто тысяч солнц, мы же возьмём всего десять тысяч светимостей солнца), и при этом светила достаточно долго, при выбранной светимости срок высвечивания гравитационной энергии 10тысяч лет – вполне исторически значимое время, которое могло бы показаться «вечным» для молодой цивилизации в находящейся неподалёку звёздной системе.

Итак, рассмотрим такой «абсолютно невозможный» гипотетический сценарий – на первом этапе за сравнительно короткое время из первичного облака образовалось протосолнце массой в 50% нынешнего Солнца, средней плотностью в 20 единиц, состоящее из тяжёлых элементов, а вокруг него вращается остаток облака, массой примерно в оставшиеся 50% МС. Фактически мы из условия описанного в главе 2.3 перепрыгиваем от ядра массой 5—10% МС к ядру многократно большего размера, вообще без всяких промежуточных обоснований. Единственно, для обоснования теоретической правомерности такого перехода напомню, что звезда Ross-508, с плотностью в 26 единиц, имеет массу 18% Солнца, и радиус в 21%, то есть сделанное предположение не столь и фантастично, а очень даже близко к возможному. В результате, мы имеем вращающееся облако, которое уже обеднено металлами, по сравнению с исходным своим составом, но их всё ещё предостаточно и для выпадения на протосолнце, до достижения им массы порядка 60—70% МС (имеются в виду только металлы), и для образования будущих планет. Какую картину мы в результате должны увидеть?

Итак, в первой фазе рождения звезды (глава 2.1) вода уже сгустилась в грязные снежинки-капли, которые в основном выпали в область протопланетного диска, и вращаются там в облаке газа почти по круговым орбитам с почти первой космической скоростью для данного расстояния от протозвезды. Эти капли падают сквозь газ на протозвезду массой в половину МС, которая при плотности всего в 20 единиц (в 15 раз плотнее нынешнего Солнца), должна иметь объём порядка 3% от объёма Солнца, то есть линейный размер в 30% солнечного. А значит, выпадение массы в одну Землю (1МЗ) на поверхность этой протозвезды выделит энергию в 1.5 раза выше, чем падение такой же массы на поверхность нынешнего Солнца, которая по формуле E=G*МС*МЗ/Rc (из главы 1.) составляет порядка 10^36Дж, или светимость Солнца за 100 лет. То есть фактически, если у нас ежегодно на протозвезду будет выпадать «всего» 60МЗ вещества любого химического состава (около 2млн. куб. км в секунду, это слой в 120км в год на всю поверхность Солнца при плотности воды, или 6км при плотности 20 единиц), то это вполне обеспечит выделение энергии на уровне 10^4 солнц. А при условии, что выпасть ещё должно около 50%МС что равно 150000 МЗ, то у нас имеется огромный запас времени свечения такой квазизвезды.

Что же мы должны в этом случае увидеть со стороны? Безусловно, при падении вещества на поверхность протозвезды, основная часть энергии выделяется именно на последнем этапе, почти у поверхности протозвезды, так как именно там и наибольшая гравитация, и падающее вещество должно погасить свою первую космическую скорость практически до нуля на очень короткой дистанции, но кое-что будет постепенно выделяться и на большом расстоянии от протозвезды из за трения о газовую атмосферу. И потому, если бы мы могли видеть сквозь толщу газового облака, центральная протозвезда должна бы предстать пред нами как чрезвычайно яркий, синий или даже ультрафиолетовый карлик. Вот только, она скрыта от нас мощным окружающим облаком, хоть и чрезвычайно рыхлым, но, благодаря высоте в миллионы километров, с оптической плотностью в миллионы тонн на квадратный метр. То есть видимым для нас светящимся диаметром квазизвезды будет что-то типа Бетельгейзе, только немного поменьше. Так как мы выбрали для квазизвезды (произвольно) светимость в 10 раз меньше Бетельгейзе, то при такой же как у неё температуре поверхности, она должна иметь в 10 раз меньшую площадь поверхности, или примерно в 3 раза меньше радиус квазизвезды – то есть радиус видимой границы будет проходить где-то на орбите Марса (1.5 АЕ). Если же поверхность квазизвезды будет холоднее, чем у Бетельгейзе (3600°К), например на 20% (=3000°К), то при сохранении светимости размер будет на 45% больше, и орбита Марса полностью окажется внутри квазизвезды, с большим запасом, вплоть до орбиты мифического Фаэтона, и только нынешняя орбита Юпитера будет вне светящейся границы звезды.