
Полная версия
Формирование звёзд и планет с точки зрения школьной физики. Детальный алгоритм рождения звёзд и появления планет, и следствия из него
Глава 2.5 Вторая стадия образования собственно солнца, версия его строения
И наконец, начинается часть вторая – образование звезды из квазизвезды. Есть квазизвезда, диаметром в несколько АЕ, и в момент своего образования она имеет наивысшую за всю свою историю массу. Её гало, будучи нагретым до сотен или тысяч градусов энергией гравитационного сжатия, активно излучает в красном-инфракрасном диапазоне, и едва отличимо от газовых гигантов. В этом гало идут процессы активного перемешивания газа, и потому его температура почти постоянна по всему объёму газа, имея только резкий скачок близ центра, у протосолнца, и резкое падение на краю, где происходит высвечивание энергии в космос, а так же испарение в космос самых быстрых атомов из очень неглубокого гравитационного колодца. И чем моложе квазизвезда, тем она крупнее и холоднее её наружная оболочка.
Выпадение остатков газа из исходной разрежённой туманности на поверхность гало сопровождается сильной потерей им углового момента вращения. Точнее сказать – происходит сепарация массы вещества, при которой на протосолнце выпадает вещество с малым моментом вращения, а в облаке остаётся с большим. Происходит это следующим образом.
В газовом облаке, вращающимся вокруг протозвезды, и имеющем размер в несколько сотен нынешних размеров солнца, средняя плотность газа и так не велика, а на периферии облака она совсем маленькая. В результате, среднее время между столкновениями частиц (атомов или молекул) в этой разрежённой области может исчисляться минутами, если не часами, а внутри облака – только доли секунд. При этом в среднем масса газа достаточно равномерно вращается, с той же скоростью, как и более плотные нижележащие слои газа. Рассмотрим, что происходит в этом облаке с атомами (или молекулами). В некоторый момент произошло соударение двух частиц, и их разлёт, после чего обе они полетели по отрезку обычной кеплеровской траектории частицы, находящейся в гравитационном поле планеты – то есть по кускам эллипсов. А общая масса газа в среднем имела движение по круговой траектории. При этом разлетевшиеся частицы имеют скорости, отличные от средней скорости газа – у одной добавочная скорость окажется сонаправлена со скоростью газа, а у другой направлена в противоположную сторону (поперечная составляющая скорости нам не интересна). В результате, в момент следующего соударения, положение частицы, имевшей меньшую скорость, окажется внутри круговой траектории, то есть ближе к протозвезде, а положение более быстрой частицы будет вне этого круга, то есть она окажется дальше. И величина отклонения обеих частиц от круговой траектории будет пропорциональна квадрату времени свободного полёта до следующего соударения.
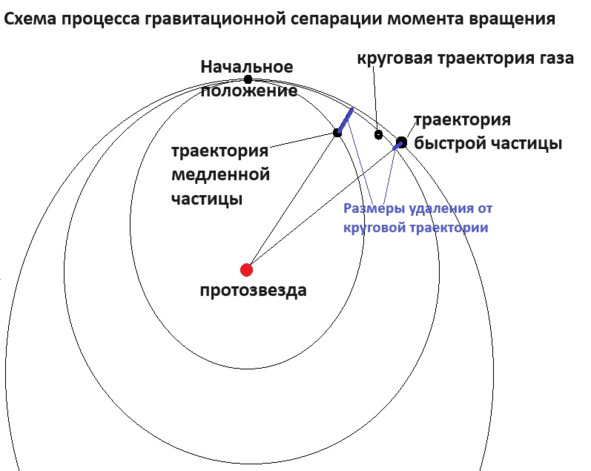
И таким образом сепарация происходит повсеместно, по всему объёму облака, но в плотной её части эффект оказывается мизерным, зато во внешней области, где соударения редки, скорость сепарации возрастает на порядки. В результате сепарации большая часть массы облака может выпасть на квазизвезду, обладая малым моментом вращения, а остатки газа с большим моментом вращения, частично передадут его снежинкам в плоскости пылевого диска, или поднимутся на более высокие траектории.
Этот процесс сепарации момента вращения и выпадения вещества может продолжаться тысячи или миллионы лет. Одной только воды (массой 3000МЗ) выпадает столько, что на поверхности протосолнца получается океан глубиной свыше в 10000 километров, если считать размер протосолнца в 10% размера Солнца! То есть, даже без учёта веса водорода, метана и аммиака, одна лишь вода создаёт на наружной поверхности протосолнца давление в десятки миллионов атмосфер.
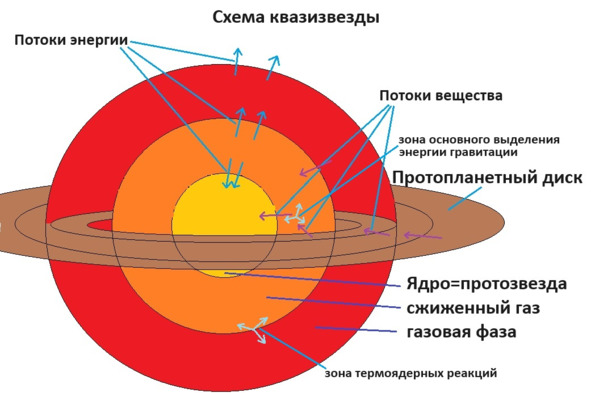
При этом, до начала термоядерных реакций, протосолнце всё так же остаётся твёрдо-жидким (не газообразным) монолитом – огромное давление не позволит ему закипеть. Низкая начальная температура ядра определяется не только активным теплоотведением хорошо перемешивающейся газовой атмосферы, но и обратной связью – как только температура у поверхности протозвезды вырастает до испарения пород при текущем давлении на слишком большом от протозвезды расстоянии, так сразу падение вещества прекращается, и тем самым исчезает источник подвода энергии. Всё вместе это определяло низкую начальную температуру поверхности протосолнца не более чем в 10тыс. градусов (внутри впоследствии стало горячее из-за радиоактивного распада). Как и на Земле, пока давление было не слишком высоко, центр протосолнца плавился, и в нём шли магматические процессы с переносом тяжёлых элементов ближе к центру, а лёгких на поверхность. Из-за обилия в центре протосолнца воды и водорода, лавы были очень жидкие, подвижные, с большой скоростью разделения пород на фракции. Уже в первые столетия существования протосолнца, ещё до появления собственно квазизвезды, в нём создаётся жидкое железное ядрышко, в котором возникают электрические токи, приводящие к образованию магнитного поля, которое быстро усиливается до максимально возможных значений. Внешняя граница протосолнца становится каменной, как на Земле, над ней плещется раскалённый океан глубиной в тысячи километров, растворяющий несколько десятков верхних километров каменной мантии. Температура этого океана, учитывая давление и солёность, может быть в тысячи градусов. Океан тоже электропроводен, и потому добавляет магнитного поля протосолнцу.
Затем, после выпадения большей части массы первичного облака, давление в ядре увеличивается настолько, что всё застывает обратно в твёрдой фазе, даже невзирая на рост температуры, затвердевает даже часть океана. Далее после оседания большей части гало квазизвезды на протозвезду, повышения внутри температуры до десятков-сотен тысяч градусов, начинаются термоядерные реакции – быстрее всего в нижней зоне газовой оболочки, но не в ядре, потому что там хоть и много водорода, но его процентное содержание невелико. Но когда они начинаются, Солнце не сразу раскаляется – ему надо нагреть не только разряжённую газовую фотосферу выше зоны термоядерных реакций, но и очень массивное сравнительно холодное ядро. И пока протосолнце медленно нагревается, на него могут выпадать всё новые порции водорода из гало, всё больше повышая давление, и процессу падения ещё не противостоит излучение.
А когда термоядерные реакции наберут силу, и прекратят приток массы водорода, каменное ядро уже претерпит огромное сжатие, и диффузия любых атомов станет исчезающе малой. Вследствие этого, даже за миллиарды лет протосолнце не перемешается с внешними слоями, сохраняя в себе огромный запас тяжёлых элементов. А в фотосферу Солнца перейдёт лишь то, что уже было растворено в жидком водяном океане, да ещё то, что упало сверху в виде зародышей планет на самой последней стадии. В результате получается, что фотосфера нынешнего Солнца должна быть сильно обеднена теми элементами, которые не могут вырваться из ядра, и наоборот – обогащена теми, которые легко из неё вырывались ещё на стадии формирования протосолнца.
Таким образом, пятая особенность моей теории – карликовая звезда типа Солнца с самого момента его появления НЕ является гомогенным образованием, просто по факту построения. Оно исходно имеет внутреннюю область богатую самыми разными тяжёлыми элементами, и наружную область, состоящую из летучих газов, впоследствии превратившихся в плазму. При этом само ядро Солнца на разных глубинах должно иметь разный химический состав.
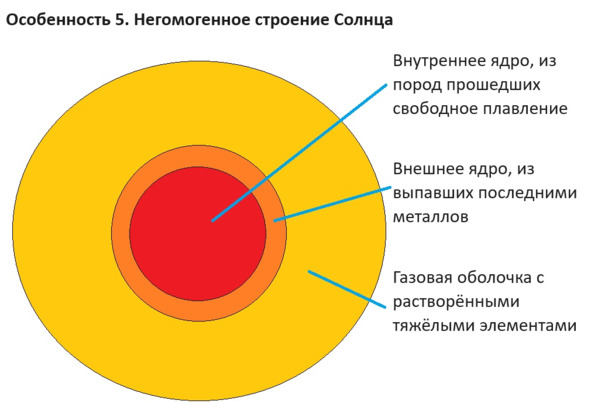
Отсюда следует, что реальные пропорции элементов внутри как исходного облака, так и итоговой звезды, должны быть совсем иными, нежели ныне наблюдаются в фотосфере Солнца. Ядро Солнца, состоящее почти целиком из тяжёлых элементов, может достигать 10—90% массы и 1—20% радиуса Солнца. А над ним должен плескаться достаточно толстый, но сравнительно разреженный океан водорода с гелием и прочими примесями, удерживаемый на месте и стабилизируемый именно притяжением гигантского ядра. И если ядро Солнца свыше примерно 50% массы, а фотосфера достаточно тонкая, дающая малое давление, то в верхней части ядра может быть пограничный незастывший слой с возможным движением магматических пород.
Глава 2.6 Обоснование негомогенной версии строения Солнца
А теперь обоснуем тот факт, что если Солнце исходно появилось с каменным ядром, то ядро Солнца до сих пор не могло раствориться в окружающей водородной атмосфере до гомогенного состояния. Если внутри звезды должно быть повышенное количество металлов, по сравнению с её поверхностью, то должно быть и постепенное нарастание концентрации металлов с глубиной. Попытаемся рассчитать, с какой скоростью должно происходить изменение концентраций разных элементов в зависимости от глубины. Для этого сперва отвлечёмся от Солнца, и снова посмотрим на Землю.
Как известно, наша земная атмосфера в основном состоит из двух газов – кислорода и азота, до высоты 50км с незначительной примесью прочих газов, и на уровне моря содержание кислорода 20.7%, а на высоте 20км уже 18%. А какие ещё есть цифры? Посмотрим на такую табличку:
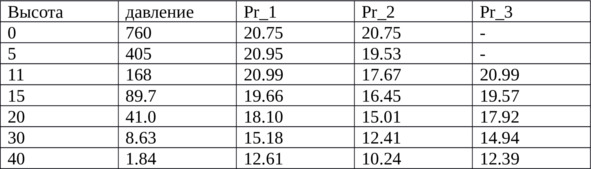
В ней первые 3 столбца табличные, взяты из интернета – высота над уровнем моря в километрах, давление (мм рт. ст.) и Pr_1=% кислорода на данной высоте. Но это реальные данные, полученные многочисленными измерениями реальной атмосферы, в которой есть горизонтальные ветра, и даже вертикальные потоки воздуха. А как бы этот процент рассчитать приблизительно, в идеальных условиях и без ветров? То есть задача такова – как посчитать парциальные давления разных идеальных газов в смеси, в узкой вертикальной трубке, в зависимости от высоты и разной температуры на разных высотах?
Это задача повышенной сложности для школьного уровня, и ответ на неё следующий. Если мы возьмём трубку со смесью идеальных газов разной плотности, подержим её до установления равновесия, затем мысленно разделим содержимое по нескольким таким же трубкам – в каждую уйдёт свой газ, и атом передвинется на ровно ту же высоту, на которой он находился в исходной трубке, то в итоге получим несколько трубок с газами, уже находящихся в динамическом равновесии – то есть газы в них не будут двигаться вверх-вниз, а уже будут распределены в точности по экспоненциальным законам. А раз так, то формула расчёта состава смеси по высоте просто элементарна – берём сумму экспонент, со скоростями роста пропорциональными молярным массам составляющих, с краевым условием что на опорной высоте значения концентрации должны быть табличными, после чего ищем значение концентраций на той высоте, где рассчитанное давление равно реальному. И температура газа на какой-либо высоте попросту не участвует в формуле.
Теперь проверяем, насколько эта формула расслоения идеальной атмосферы близка к реальной. Берём из таблицы опорную высоту в 0км, и считаем по указанной формуле содержания кислорода (столбец Pr_2). На высотах 20—40км получилось что-то похожее на табличные значения, только с 1.5—2.5 раза отличающейся скоростью падения концентрации, а на 5 и 11км – совсем плохое совпадение, ибо реально до 11км содержание кислорода оказывается растёт, а не падает! То есть, из за не идеальности газов и происходящих в атмосфере химических процессов, для малых высот формула не предсказала вообще ничего, а на больших высотах отличие от реальности всё же слишком большое. Раз так, то считаем концентрации ещё раз, взяв теперь опорную высоту в 11км, получаем новый столбец значений Pr_3, и опаньки – рассчитанные значения почти идеально ложатся на реальные данные, ошибка прогноза менее 10%! Это значит, что при всех тех ветрах, которые дуют в атмосфере Земли, концентрации газов по высоте ведут себя почти по идеальному закону. Правда, тут следует оговориться, что в верхних слоях атмосферы ветра всё же в основном горизонтальные, а вертикального переноса воздушных масс практически нет.
А раз так, раз формула даёт приближение с очень хорошей точностью, то стоит приглядеться к тому, что именно покажет та же самая формула для Солнца.
Для начала лирическое отступление. То что указано в Википедии о содержании элементов в фотосфере – это значения явно верхних слоёв, но непонятно, насколько верхних. Так как мы на Земле увидели этот свет, без последующего переизлучения, значит он дошёл до нас с глубины прозрачности фотосферы. Земная атмосфера для нас более чем прозрачна при взгляде строго вверх (оптическая плотность 10тонн на кв. метр), и вполне близка к прозрачной при взгляде на горизонт (около 100тонн). Значит, будем считать, что исходно мы зафиксировали концентрации газов по центру солнечного диска, когда смотрим строго вглубь на максимально возможную глубину прозрачности фотосферы (порядка 10—100км), хотя при взгляде на край диска некоторые концентрации могли немного поменяться.
Итак, мы зафиксировали концентрации элементов (по числу атомов) на некотором слое, там, где для удобства давление назовём одной «атмосферой», и далее посчитаем, какие концентрации газов должны быть на глубинах, соответствующих давлениям 10, 100, 1000 и 10000 «атмосфер». Из всего списка химических элементов, присутствующих во внешних слоях Солнца, в таблицу взяты самые массовые, непохожие по динамике на остальные, например углерод и азот пропущены потому, что их динамика почти не отличается от динамики концентрации кислорода. Вот какая получается табличка:
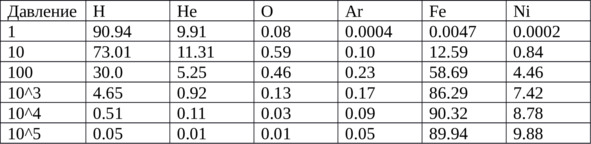
Как видно из таблицы, если бы на Солнце фотосфера была бы хоть сколько-то близка к идеальной, то уже на глубине, где давление равно 100 «атмосферам» концентрация водорода и гелия была бы мала, а основу составляло бы железо. А если бы в верхних слоях был замечен более тяжёлый свинец в количестве 1 атом на триллион (даже не миллиард), то при 100 «атмосферах» железо бы составило 3.8% а свинец 33% атомов! При этом, для данной формулы совершенно без разницы, где именно, то есть на какой глубине, наступает вертикальная стабилизация фотосферы Солнца – на глубине тысячу км, или пять тысяч, или даже сто тысяч км – как только такая стабилизация наступила, если только газ хоть как-то похож на идеальный, то на глубинах с 10- и 100-кратно большим давлением распределение элементов будет близко к указанному в таблице.
Таким образом, есть все основания считать, что даже если внешняя часть атмосферы Солнца сильно перемешивается по вертикали, и плазма далека от смеси идеальных газов, то в зоне лучистого переноса энергии, к глубине начала того образования, которое астрофизики именуют водородным ядром (10млн атмосфер обычных) концентрация элементов вследствие разделения должна приблизиться как минимум к рассчитанной на глубине в 100—1000 «атмосфер». То есть, ни о каком преобладании водорода уже не может быть и речи, и уже одно это доказывает ошибочность текущей картины внутреннего состава Солнца.
Часть 3. Общее описание процесса образования планет – теория каменного дождя
Глава 3.1 Процесс формирования зародышей планет от пыли до снежков килотонной массы
Теперь стоит вернуться к исходному вопросу ребёнка— а как же образовались наши планеты? Итак, откатываемся назад, ко временам появления протозвезды, ещё без образования квазизвезды. У нас уже есть «тёплое» каменное протосолнце, то есть уже нагревающее грязный лёд до липкого состояния, но и не раскалённое до возможности быстрого высушивания снега, и относительно тонкий протопланетный диск, образовавшиеся буквально за тысячелетия или десятки тысяч лет, состоящий из огромного числа снежинок и газа, общей плотностью возможно до нескольких тонн на квадратный метр площади этого диска (но распределённых по высоте эклиптики на сотни тысяч километров), из которых на твёрдое вещество приходится порядка 1% массы, то есть десятки килограмм. Значит, при подобной плотности тёплые и липкие снежинки начинают при столкновениях массово слипаться в комки, вопрос лишь – с какой скоростью?
Допустим, что исходно у нас первичный материал для образования планет находится на достаточно высоких орбитах (и лишь впоследствии упадёт поближе к Солнцу), и распределён совсем тонким слоем – непосредственно твёрдых частиц (льда и тяжёлых элементов) буквально 10кг на 1кв. метр диска – в переводе сплошной на водяной лёд, толщина =1см. Тогда для образования Юпитера с массой 1.8*10^27кг понадобится диск диаметра порядка 10^10км, что на порядок больше диаметра его нынешней орбиты, то есть минимальная оценка плотности диска более чем правдоподобна. Весь этот диск можно условно поделить на отдельные круговые орбиты, как делится на отдельные кольца диск вокруг Сатурна. Допустим мы рассматриваем отдельную орбиту, на которой один оборот длится 400млн секунд (≈13 лет) – взяли красивую круглую цифру. Каждая частица в течение оборота вокруг Солнца четверть оборота поднимается над математическим экватором, потом столько же опускается, потом поднимается и опускается с противоположной стороны, каждый интервал по 100 млн секунд. Представим, что исходно у нас все частицы идеальные, двигаются как газ, с постоянной для всех температурой – мерой средней кинетической энергии. Это значит, что средняя кинетическая энергия любой частицы – постоянна, и одиночной молекулы водорода, и снежинки весом в целый грамм. Один грамм, это по весу примерно 6*10^23 атомов водорода (число Авогадро), округлим его до 10^24, а значит, если средняя скорость отдельного атома водорода километр в секунду, то средняя скорость граммовой снежинки уже всего нанометр в секунду. Фактически перед нами картина тепловой смерти – снежинки не могут слипаться просто потому, что практически не двигаются! Где же ошибка в вычислениях?
Ошибка в том, что мы рассматриваем не просто газ, а находящийся в гравитационном поле. Итак, введём координатные оси во вращающейся системе координат, относительно частицы вращающейся строго по кругу, не покидающей экватора – ось X направлена к солнцу, ось Y по направлению вращения идеального математического экватора, ось Z вверх от плоскости экватора. Тогда при столкновениях частиц. находящихся примерно на одной орбите, скорости сталкивающихся частиц по осям X и Y свободно взаимоуничтожаются, а вот по оси Z всё гораздо сложнее. Дело в том, что мы неявно предполагали, что все частицы столкнутся на самом экваторе, когда потенциальная энергия у них нулевая (наименьшая на данной орбите), а кинетическая энергия максимальна, а ведь это не так. Проведём мысленный эксперимент – возьмём всё пылевое облако, разобьём его на кубики размером 1км, все твёрдые частички из каждого кубика мгновенно слепим в одну снежинку внутри кубика, сохранив за ней среднюю скорость и координаты частиц, из которых эту снежинку слепили. Тогда у этих снежинок окажется практически нулевая скорость относительно экватора по любой из выбранных координат, но совсем не нулевая высота, которая в гравитационном поле сразу же начнёт обратно преобразовываться в скорость, которая достигнет на экваторе уже сотен м/сек! Так что, тепловой смерти нет, надо только правильно посчитать средние скорости движения.
Проведём следующий мысленный или численный (у кого есть компьютер и знания программирования) эксперимент. Итак, допустим, у нас на орбите летят частицы, которые должны слипнуться в снежинки, и для простоты вычислений предположим, что слипаться могут только частицы одинаковой массы. В начале эксперимента, на 0 шаге, это были атомы водорода, со скоростями до 1км/сек. На каждом следующем шаге сталкиваются любые две случайно выбранные частицы, находясь в любом случайно выбранном месте своей орбиты, вне зависимости от места предыдущего столкновения, их скорости гасятся, но потенциальная энергия остаётся. Проводим математическое моделирование (на уровне программирования для 10 класса), и получаем такую табличку:
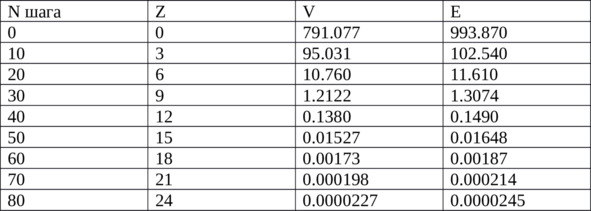
Здесь у нас N= номер шага (кратно 10), Z=десятичная степень числа атомов в снежинке (10^Z ≈ 2^N, 10^3 ≈ 2^10), V и E= средняя арифметическая и среднеквадратичная скорость частиц в момент пересечения экватора.
Полученное моделирование показывает, что вертикальная скорость падает пропорционально не квадратному, а кубическому корню из количества атомов в снежинке. И для граммовых снежинок (Z=24) составляет порядка 0.02мм/сек, что на 4 порядка выше, чем вычисленное из просто теплового движения. И если полный оборот длится 400млн секунд, то такая снежинка будет летать относительно экватора вверх-вниз на несколько километров, массово сталкиваясь с себе подобными. Какова будет реальная средняя скорость – как при моментальном слипании (до километра в секунду), или как при очень длительном (десятки микрон в секунду) – сразу сказать невозможно, но мы хотя бы теперь знаем ограничение на скорость снизу.
Что из этого следует? Почти все пылинки за несколько оборотов вокруг Солнца гарантированно слипнутся в снежинки, диаметром минимум в толщину снежного покрова, просто выложенного на экватор. Мы предположили, что льда там будет 10кг на метр, толщиной 1см, но снег ведь гораздо более рыхлый – его толщина минимум 10см. Значит, на первом этапе, на каждой орбите, буквально за первые несколько оборотов вокруг ещё протозвезды, мелкие льдинки обязаны слипнуться в кубические снежки размером в 10см, прилегающие вообще без зазоров, или более вероятно – в круглые снежки диаметром по 20см (=0.4 кг) с расстояниями между проекциями центров на экватор около 22см, имеющими характерную вертикальную скорость около 1 микрона в секунду минимум. Вес получившихся снежков, конечно, мал, но и скорости микроскопические, а это значит, что гравитационное притяжение между ними станет существенным (а ведь ещё возможно и гораздо более сильное электростатическое притяжение). Ведь если два килограммовых снежка пролетают мимо друг друга на расстоянии в 1м на скорости 10^-6 м/с, за миллион секунд гравитационного взаимодействия они наберут скорость порядка 10^-4 м/с – в сто раз больше, чем была их вертикальная скорость! А значит, почти гарантированно столкнутся и слипнутся. А раз так, то производим очередной расчёт – как поведут себя пылинки пролетая мимо крупного снежка плотностью 0.1, массой m, на малых скоростях (10, 1, 0.1 и 0.01 мм/сек) на разных расстояниях.
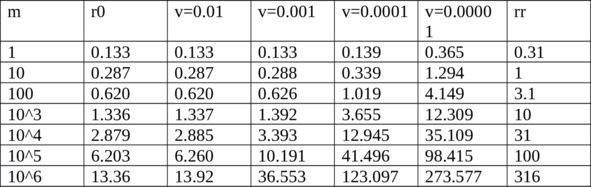
В таблице указаны масса m в килограммах, и r0= радиус снежка в метрах, далее 4 столбца значений – на каком расстоянии от центра снежка исходно должна была пролегать неискривлённая прямая траектория пылинки, пролетающей с указанной скоростью (от 0.01 до 0.00001 м/сек), чтобы траектория искривилась настолько, чтобы пылинка врезалась в снежок. Речь здесь о пылинке потому, что более крупный снежок будет обладать ненулевым радиусом, и врежется на ещё большем расстоянии. Последнее поле rr= среднее расстояние между проекциями снежков на экватор, если бы абсолютно все снежки имели бы одинаковую указанную массу.
Из таблицы видно, что даже снежки от 1кг до 100т при характерной скорости 0.01мм/сек будут иметь дальность гравитационного захвата чуть больше среднего расстояния между снежками, а значит будут очень быстро сталкиваться с увеличением массы до килотонны. Можно возразить, что при мизерных горизонтальных скоростях сталкиваться будет не с кем, ибо снежинка только и будет делать, что двигаться вверх-вниз относительно экватора, без бокового смещения. Но пролёты не закончившиеся столкновениями, из за гравитационных взаимодействий очень быстро изменят вектора скоростей снежков с чисто вертикальных на хаотические по всем трём координатам.
Начиная с некоторого момента потенциальная энергия расстояний между снежинками станет не просто переходить в кинетическую, с дальнейшим переходом в тепловую (при столкновении) или обратно в потенциальную (при пролёте), а при взаимодействии многих тел некоторые снежки неизбежно будут отбрасываться с большими скоростями, вследствие чего средняя скорость снежинок начнёт потихоньку возрастать. И например, снежок массой в килотонну, при скорости набегания в 1мм/сек имеет радиус зоны захвата уже не 273м, как при скорости 10мкм/сек, а всего 36м, при среднем расстоянии между проекциями снежков на экватор порядка 316м. то есть, вроде бы, ему теперь уже не с кем стало столкнуться. Тогда делаем такое вычисление. Допустим на данной орбите год=400млн. сек, средняя скорость снежков уже килотонной массы 1мм/сек, значит средняя высота подъёма снежков над экватором составит около 50км, толщина слоя полёта 100км. А снежки (в исходно раскатанном в блин виде) занимают слой толщиной 10см, что в миллион раз тоньше зоны полётов снежков. Значит, каждый кубометр снега приходится на 1млн кубометров пространства зоны возможного пролёта снежков. Снежок массой в килотонну, летящий вбок со скоростью 1мм/сек, за один «год» проходит расстояние в 400км, и заметает зону притяжения радиусом 36м, площадью сечения 4000кв. м, объёмом за год 1.6млрд кубометров, из которых каждый 1 из миллиона кубометров занят снегом. А это значит, что за год он либо встретится с пылинками общим объёмом 1600кубометров и массой 160 тонн (16% массы самого снежка), либо с вероятностью 16% в эту зону попадёт не то что край, а прямо таки центр такого же снежка массой в килотонну. А если бы средняя скорость была свыше 10мм/сек, то данная вероятность составила бы порядка 1.5—2% в год. К сожалению, на этом вычисления приходится закончить, ибо без серьёзной компьютерной техники делать статистические вычисления для систем многих тел с неизвестными средними начальными скоростями – бесперспективное занятие. Но в любом случае, физика курса средней школы показывает процесс формирования зародышей планет до килотонного класса, в то время как интернет сообщает о пробеле в знаниях алгоритма укрупнения частиц планетезималей от 1 см до 1 км (например тут [2]).

