Этюды о Галилее

В своих «Cogitationes Privatae» Декарт кратко отмечает250:

Несколько дней назад мне довелось завязать дружбу с одним весьма ученым мужем, который задал мне следующий вопрос:

Камень, говорил он, нисходит от точки А к точке В в течение одного часа; он неизменно притягивается Землей с одинаковой силой и не теряет скорости, которая была ему сообщена через предыдущее притягивание. Но то, что движется в пустоте, по его мнению, движется вечно. Спрашивается, за какое время камень пройдет заданное расстояние.

Отметим прежде всего, что Декарт признавал, что получил от Бекмана и вопрос, и принципы решения251 – принципы, которые не имеют для него истинного значения, в отличие от Бекмана. Для Декарта они не более чем гипотезы, которые он, впрочем, не вполне понимает. Это не мешает ему разрешить данную проблему и даже предложить два различных решения. Бедный Бекман о таком и не просил, он лишь хотел узнать, как падают камни. Декарт этим не удовлетворился и объяснил ему, как они могли бы падать252.

Итак, вот его ответ253:

Я решил задачу. Площадь равнобедренного прямоугольного треугольника АВС представляет расстояние (движение); неравенство расстояния от точки А до основания ВС – неравенство движения254. Как следствие, AD будет пройдено за время, которое представлено ADE, и DB – за время, представленное DEBC: следует отметить, что меньшая площадь представляет более медленное движение. Но ADE составляет третью часть DEBC, а значит, AD будет пройдено в три раза медленнее, чем DB.

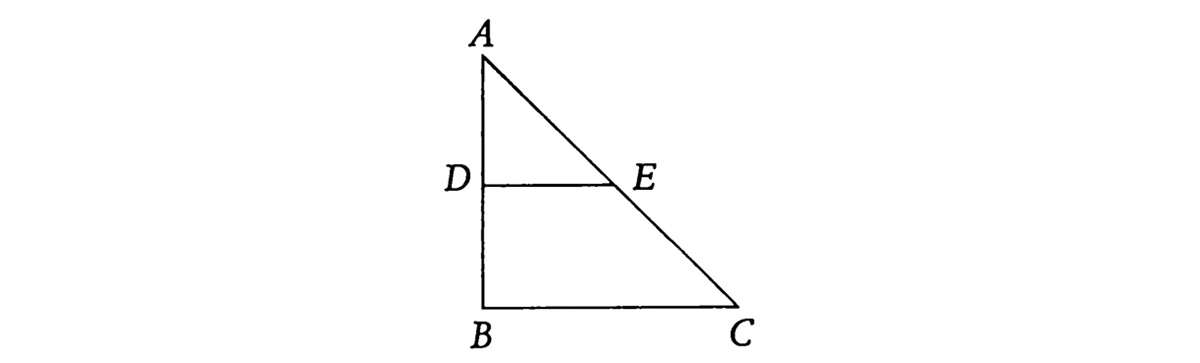
Но этот вопрос можно было бы поставить и иначе, именно: [допустим,] что сила притяжения Земли равна силе, которую оно производило в первый момент, и что новая производится, тогда как предыдущая продолжает существовать. В таком случае проблема разрешалась бы при помощи пирамиды.

Любопытное дополнение! Совершенно ясно, до чего проблема физического механизма свободного падения чужда мышлению Декарта. Его отнюдь не останавливает то, что у Бекмана уже есть решение. И он воображает иной «возможный» случай, в котором сила притяжения возрастала бы с каждым мигом – так, что во второй момент тело притягивалось бы с удвоенной силой, в третий – с тройной силой и т. д. В таком случае, разумеется, тела бы падали куда быстрее255.

Как могло бы быть возможным подобное возрастание «силы притяжения»? Декарт не задается этим вопросом. В действительности он рассматривает проблему не как физик, а как чистый математик, чистый геометр: для него задача заключается в том, чтобы установить соотношение между двумя последовательностями переменных величин. Почему бы, раз уж представился случай, не проверить забавную гипотезу?

Декарт – геометр, чистый математик. Именно в этом, видимо, заключается причина, по которой он не вполне понял «принципы» Бекмана и дал ошибочный ответ на его вопрос. Он видит проблему, как и сам исследуемый феномен, совершенно иначе, чем Бекман.

Так же как и Бекман, он исходит из завершившегося движения свободного падения. Но в отличие от него, Декарт видит это движение в некотором смысле «приостановленным». Или, если угодно, он рассматривает лишь траекторию свободного падения тела, или, если угодно, сформулируем это иначе – он инстинктивно элиминирует время.

Для Декарта линия ADB, которая для Бекмана представляла затраченное время256, естественным образом представляет пройденный путь. И проблема видоизменяется: путь пройден с «равномерно изменяющейся» скоростью; проблема, таким образом, заключается в том, чтобы определить скорость в каждой точке пути. Треугольники ADE, ABC, которые у Бекмана представляли пройденное расстояние (траекторию), у Декарта представляют движение предмета, т. е. «сумму скоростей», которые были достигнуты. И он делает весьма правдоподобное заключение: если «сумма скоростей» утраивается, то расстояние DB будет пройдено в три раза быстрее. Время отыскивается, но слишком поздно: крайняя геометризация, пространственное представление, элиминация времени (там, где его нельзя элиминировать), пренебрежение физическим, каузальным аспектом этого процесса – все это приводит Декарта, как когда-то привело Галилея, а до него – Бенедетти и Мишеля Варрона, к тому, что он мыслит равномерно ускоряющееся движение как движение, скорость которого возрастает пропорционально пройденному пути, а не пропорционально затраченному времени.

Итак, если мы вправе произвольно определять наши понятия, нам также следует – именно этот урок нам преподаст Галилей – стремиться к пониманию сущности природных явлений. Иными словами, нам нельзя пренебрегать причинами и забывать о времени.

***

Мы только что установили, что Декарт не вполне вник в «принципы» физики Бекмана. Можно было бы пойти еще дальше и сказать, что он не понял, насколько далеко удалось продвинуться его товарищу257. Правда, и сам Бекман не вполне это понимал. В подтверждение нашего анализа причин декартовской ошибки приведем текст «Physico-mathematica», который, как нам кажется, достаточно полно раскрывает это непонимание. Процитируем весь этот отрывок258.

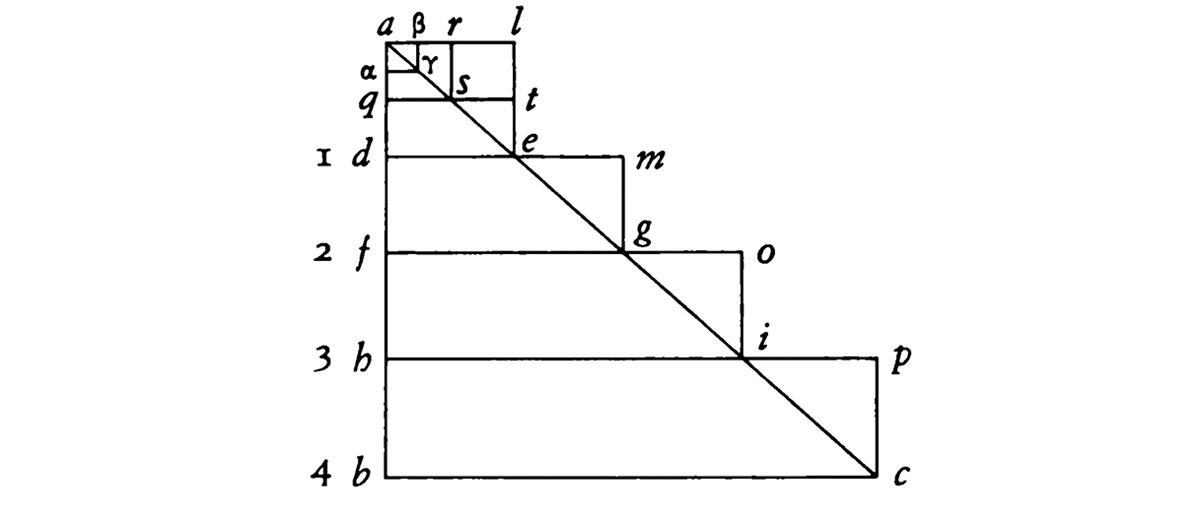
В поставленном вопросе, где говорится, что в каждый момент времени259 прибавляется новая сила [к той], с которой тяжелый предмет стремится вниз, я говорю, что эта сила возрастает таким же образом, каким возрастают поперечные линии de, fg, hi и прочие, бесконечное множество которых можно представить между теми. Чтобы доказать это, я допущу, что первый минимум или точку движения260, произведенного первым действием силы притяжения Земли, можно представить с помощью квадрата alde. Для второго минимума движения у нас будет вдвое больший квадрат, а именно dmgf: действительно, первая сила, которая присутствовала в первом минимуме, остается, а другая, новая, прибавляется к ней, и она равна предыдущей. Таким же образом в третьем минимуме движения будут три силы, а именно: первая, вторая и та, что относится к третьему временному минимуму, и т. д. Однако это число треугольное, как я далее объясню более пространно, и, по-видимому, представляет треугольник abc. Тем не менее, скажешь ты, есть же выступающие фигуры ale, emg, goi и т. д., которые выходят за границы фигуры треугольника. Следовательно, фигура треугольника не сможет выражать рассматриваемое движение. Однако, отвечу я, эти выступающие части возникают из-за того, что мы наделили протяженностью те минимумы, которые нужно представлять как неделимые и не состоящие из каких-либо частей. Это доказывается следующим образом. Я поделю минимум ad точкой q на две одинаковые части; тогда arsq будет первым минимумом движения, а qted – вторым минимумом движения, в котором будет два минимума сил. Таким же образом мы разделим df, fh и т. д. Тогда мы получим выступающие части ars, ste и т. д. Очевидно, что они еще меньше, чем выступающая часть ale. Пойдем еще дальше. Если я допускаю для минимума еще меньший минимум, такой как aα, выступающие части будут еще меньше – как αβγ и т. д. Если, наконец, для этого минимума я возьму действительный минимум, т. е. точку, тогда эти выступающие части будут нулевыми, поскольку они не смогут быть целиком всей точкой, но, очевидно, будут лишь частью минимума alde, а часть точки есть нуль.

Отсюда ясно, что если мы представим себе, например, камень, который притягивался бы Землей в пустоте от а к b с силой, которая всегда исходила бы от нее одинаковым образом, в то время как предыдущая оставалась бы, то первое движение в а относилось бы к последнему, которое находится в b, как точка а относится к отрезку bc. Что касается промежутка gb, то камень прошел бы ее в три раза быстрее, чем другой промежуток, ag, ибо он бы притягивался Землей втрое большей силой.

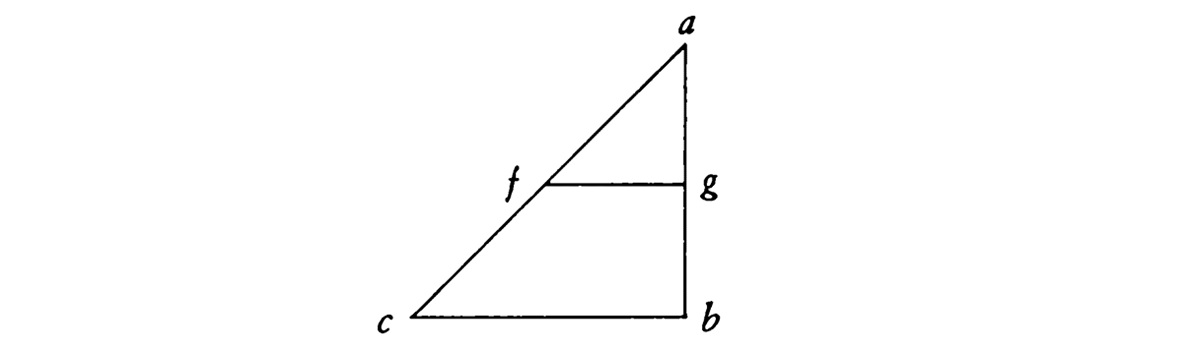
В самом деле, площадь fgbc составляет утроенную площадь afg, и это легко доказать. Таким образом, сообразно пропорции, следует то же самое утверждать и обо всех остальных частях.

Трудно себе представить другой текст, который объединял бы в себе высшее математическое изящество261 и настолько непростительную с точки зрения физики ошибку. Определенно, Декарт не понимал «принципов» Бекмана; и он просто-напросто упустил из виду его интеллектуальный прорыв – принцип сохранения движения. Декарт заменяет движение силой. Он отталкивается от идеи, что скорость пропорциональна силе262, и заключает из этого, что постоянная сила производит постоянную скорость. Таким образом, он возвращается к идее классической физики – к идее импетуса. Ему кажется, что если тело падает, ускоряя свое движение, то это потому, что оно сильнее притягивается Землей к концу движения, чем в начале, или, говоря словами Декарта, потому что сила притяжения Земли производит в камне возрастающую движущую силу; он также прибавляет (цитируемый фрагмент соответствует первой гипотезе, исследуемой в тексте «Cogitationes Privatae», который мы цитировали чуть ранее) действующие силы, а не только скорости263. Создается впечатление, что Декарт, принимая (гипотетически) бекмановский принцип сохранения движения, не вполне ему доверяет. Кажется, что, стремясь разрешить проблему свободного падения, он предпочитает обходиться без понятий, разработанных Бекманом, которые, очевидно, пока еще слишком новы для него, слишком необычны, слишком сложны. Действительно, идея движения, которую Бекман имплицитно вводит в оборот (это идея движения классической физики), в каком-то смысле располагается на тонкой грани между математикой (геометрией) и физикой (временностью). Эту идею очень сложно выявить, и проблема, с которой столкнулся Декарт, пытаясь ее постичь – удержаться на этой четкой грани между физикой и геометрическим пространством, – была бы (если помимо этой проблемы не было других) достаточным доказательством этой сложности. Именно в этом состоит причина, почему Декарт избегает этой идеи; движение – парадоксальная сущность, это состояние предмета, которое, однако, передается от одного предмета другому; это воплощение изменчивости, которое в то же время остается самотождественным; эта идея кажется ему «незаконнорожденной» сущностью; потому он намеренно, равно как и инстинктивно, замещает эту идею менее громоздкими и более прозрачными, более легко вообразимыми идеями264: с одной стороны, это идея движущей силы, с другой – идея траектории.

Тем не менее ему блестяще удается произвести математический вывод. Это можно понять без труда: с формальной точки зрения, действительно, не существует никакой разницы между проблемой Бекмана и проблемой, которую взамен предлагает Декарт. Не очень-то важно, о чем идет речь, – о силах, о площадях, о скоростях; речь всегда идет об одном и том же, а именно – о том, чтобы рассчитать темп изменения величины, которая равномерно возрастает по отношению ко времени. И когда Декарт мыслит силу притяжения, он с необходимостью мыслит и изменение или производство [движения] во времени. Именно тогда, когда он пытается выразить результаты своего исследования в терминах площадей, вдохновленный мысленным образом и стремлением к крайней геометризации, он и впадает в заблуждение, которого, как ни странно, даже с его теорией силы он, в принципе, мог бы избежать265. Если он в чем-то и ошибается, так это в том, что, замещая движение траекторией, он принимает за аргумент функции не время, а траекторию.

Картезианская «трактовка», переинтерпретация идей Бекмана кажется нам весьма любопытной и в то же время весьма явно проявляющей глубинные склонности человеческого духа и те сложности, которые он должен был преодолеть, чтобы прийти к этому понятию движения, что десятью годами позднее он объявит столь простым и ясным, что вовсе не нуждается в определении, так что было бы упущением не прояснить эту трактовку еще одним текстом. Надеемся, что читатель не будет возражать. Декарт между тем продолжает266:

Этот вопрос может быть разрешен еще иным, более трудным способом. Представим себе камень, пребывающий в точке А, притом что пространство между А и В пусто. Пусть сегодня в 9 часов утра впервые, к примеру, в точке В Бог сотворил силу притяжения, действующую на камень; и в последующий момент он и далее постоянно создавал новые силы притяжения, равные той, что он сотворил в самый первый момент. Эти новые силы, прибавляясь к тем, что были сотворены раньше, притягивают камень все сильнее, тем более что в пустоте предмет, приведенный в движение однажды, движется вечно. Допустим, что камень, который находился в точке А, достигает точки В в 10 часов. Если мы спросим, за какое время он пройдет первую половину пути (т. е. отрезок AG) и за какое время он пройдет оставшуюся половину, я отвечу, что камень падает вдоль линии267 AG в течение ⅛ часа, а вдоль линии GB – в течение ⅞ часа. Таким образом, действительно, следует начертить пирамиду с треугольным основанием, высота которой была бы равна AB и которая вместе со всей пирамидой была бы произвольным образом разделена горизонтальными секущими линиями. Камень будет пересекать получившиеся на линии АВ отрезки тем быстрее, чем больше тот сегмент пирамиды, которому принадлежит отрезок268.

Декарт прав, считая этот способ рассмотрения проблемы «более сложным». По сути, в данном случае он принимает принцип сохранения движения Бекмана. Но к этому принципу он добавляет постоянное возрастание силы притяжения (как видно, для этого он обращается к божественному вмешательству). Удивительное дело! Во всех возможных случаях, изученных Декартом, есть один-единственный, который он не рассматривает, а именно – тот, который ему предложил Бекман.

***

Как же вышло, что Бекман не заметил ошибки, допущенной Декартом, и не приписал целиком себе одному всю заслугу в отыскании правильного решения? Вероятно, мы никогда не сможем этого объяснить. Но мы должны признать тот факт, что Бекман, стремясь разрешить физическую проблему и ставя Декарта перед конкретным математическим вопросом, естественным образом применяет полученный ответ к поставленной проблеме. И там, где Декарт говорит «пространство», Бекман подразумевает «время»269. Вернее, там, где Декарт путает пространство и время, Бекман избегает этой путаницы. Кроме того, совершая по отношению к Декарту обратную ошибку, соответствующую той, которую Декарт допускает по отношению к Бекману, он в некотором смысле восстанавливает ситуацию. Таково в общих чертах объяснение, предложенное Г. Мило270. Признаться, иного объяснения мы не видим. Следует согласиться с тем фактом, что Бекман не замечает, что решение, предложенное Декартом, отлично от решения, которое он ставит ему в заслугу. Он не замечает, что в этом решении задействованы не те физические принципы, которые он вывел, и приписывает Декарту решение, которое он сам вычитал.

Не указывает ли это на то, что для Бекмана проблема была скорее математической и что именно в таком решении, которое включает в себя использование интегрального исчисления, он и видит заслугу своего юного товарища?

Казалось бы, можно было бы пойти еще дальше. Если Бекман не видит разницы между своим решением (скорость пропорциональна времени движения) и решением Декарта (скорость пропорциональна пройденному расстоянию), так это потому, что для него не существует разницы – эти два решения кажутся ему одинаковыми271.

Вероятно, нашим читателям это покажется крайне маловероятным. И все же… Не будем однако, забывать, что Бекман, несомненно будучи видным физиком, все же был весьма посредственным математиком; с другой стороны, мы увидим, что сам Декарт, хотя он и был гениальным математиком, все же так и не сумел признать допущенную им ошибку, ни даже, найдя правильную формулу у Галилея272, разглядеть, что она отличается от формулы, которую он некогда предложил сам. Тем самым мы вновь видим подтверждение тому, насколько сложно было вывести и осмыслить те простые и ясные идеи, к которым приучила нас классическая физика и картезианская философия. Даже для такого гения, как Галилей. Даже для такого гения, как Декарт.

***

Через десять лет после памятной встречи с Бекманом Декарту представился очередной случай подумать над проблемой свободного падения тел. В этот раз этот вопрос перед ним поставил его друг Мерсенн. И ответ Декарта разительно отличался от всего того, что он представил Бекману273, за исключением одной детали: так же как и десять лет назад, Декарт дает своему другу неправильную формулу – ту же, что он вывел ранее, – формулу, в которой скорость движущегося тела зависит не от затраченного времени, а от пройденного расстояния. Декарт пишет274:

Во-первых, я полагаю, что движение, однажды переданное некоторому телу, остается с ним бесконечно долго, если оно не отнимается от него по какой-то другой причине, т. е. то, что однажды начало двигаться в пустоте, движется всегда, причем с одинаковой скоростью275. Представьте себе груз, существующий в точке А, собственная тяжесть которого заставляет его двигаться к точке С. Я утверждаю, что если с того момента, когда он начал двигаться, его тяжесть его покидает, то он будет пребывать в одном и том же движении, пока не достигнет точки С. Но тогда он не будет двигаться от А к В ни быстрее, ни медленнее, чем от В к С. Однако, поскольку в действительности это не так, он сохраняет свою тяжесть, заставляющую его двигаться вниз и в каждый момент времени прибавляющую новые силы для спуска; из этого следует, что груз проходит расстояние ВС гораздо быстрее, чем расстояние АВ, так как, проходя первый отрезок, он сохраняет весь импетус, благодаря которому он двигался вдоль АВ, и кроме того, за счет тяжести, вновь приводящей его в движение с каждым новым мгновением, к этому импетусу прибавляется новый. Что касается пропорции, в которой возрастает эта скорость, то это показывается с помощью фигуры ABCDE. Первый отрезок действительно обозначает силу скорости, сообщенной в первый момент, второй – скорость, полученную во второй момент, третий – скорость, переданную в третий момент, и так далее. Таким образом образуется треугольник ACD, который представляет увеличение скорости груза, когда он опускается из точки А в точку С, и треугольник АВЕ, который представляет увеличение скорости в первую половину пути, пройденного этим грузом. А так как трапеция BCDE в три раза больше, чем треугольник АВЕ, то, очевидно, из этого следует, что груз пройдет от В до С в три раза быстрее, чем от А до В. Т. е. если он пройдет от А до В за три момента, то от В до С он пройдет только лишь за один момент. Это значит, что за четыре момента он пересечет вдвое большее расстояние, чем за три; следовательно, за 12 моментов – вдвое больше, чем за 9, и за 16 моментов – в четыре раза больше, чем за 9, и так далее276.

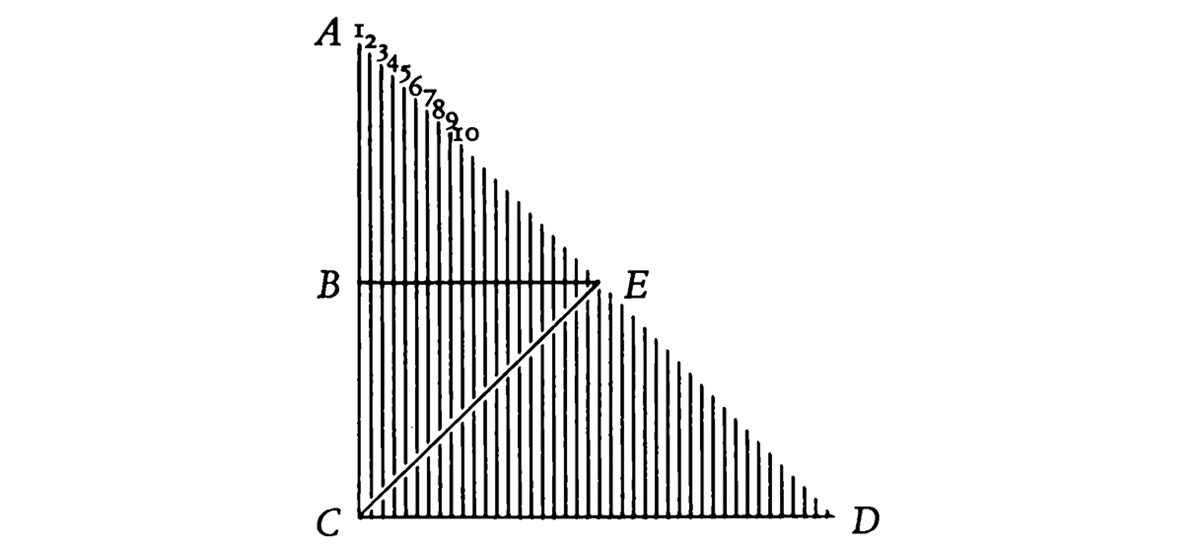
Как было сказано, решение проблемы свободного падения, которое Декарт передает Мерсенну, сильно отличается от решения, разработанного им под влиянием Бекмана. В самом деле, понятие притяжения, столь удачно использованное последним, полностью исчезло. Декарт действительно отходит от этой идеи, возвращаясь к идее импетуса, и его описание свободного падения лишь слегка отличается от того, что предлагали Бенедетти и Скалигер277: тяжесть – важнейшее качество тела, которое в каждый момент времени порождает новый импетус, заставляющий тело двигаться вниз; ускорение (выражая в терминах теории импетуса идею, сформулированную в терминах притяжения)278 объясняется тем фактом, что эти импетусы последовательно порождаются в каждый новый момент времени. Действительно, каждый импетус производит движение с постоянной скоростью; таким образом, только лишь прибавлением новых импетусов и можно объяснить ускорение. Принцип сохранения движения Бекмана действительно отныне утверждается без оговоренного ограничения (и без упоминания Бекмана), однако, как ни странно, он сводится к принципу сохранения импетуса.

Вывод формулы движения свободного падения, равноускоренного движения, также отличается от предшествующих выводов – за исключением, как уже было сказано ранее, совпадения итоговой формулы. Так же как и в предыдущий раз, Декарт путает пространство со временем, а физику – с геометрией.

В самом деле, воображая реальный, физический механизм ускорения, Декарт представляет импетусы, возникающие и порождающиеся один за другим в последовательные моменты времени. Когда же, напротив, он переходит к математическому исследованию движения, он тут же замещает время пространством, а затраченное время – пройденным расстоянием.

Фигура, которая служит основанием для его вывода, по правде сказать, не вполне ясна. Она во всем отличается от предшествующих фигур, кроме одной детали: линия АС, проходящая сверху вниз, представляет траекторию свободного падения. Как и прежде, мышление Декарта поддается искушению геометрического воображения. Его умозаключение, по-видимому, состоит в следующем: в первый момент падения – и только в этот момент – первый импетус производит движение, которое должно переносить тело в точку С с заданной скоростью. Этот импетус действует на протяжении всего пути; так, он представлен отрезком АС, который символизирует всю траекторию в целом. Второй импетус производит движение со скоростью (абсолютной), равной той, которая была произведена первым импетусом. Но он не действует с начала движения, он, скажем так, подхватывает тело на каком-то расстоянии от точки А; третий импетус начинает действовать от еще более удаленной точки279и так далее. Потому множество импетусов представлено множеством отрезков-расстояний – пройденного пути, – в продолжение которых они действуют.

Декарт, скажем так, позабыл, что импетусы возникают последовательно, или, если угодно, он представляет эту последовательность простирающейся в пространстве, вдоль траектории движения280. Так и не сумев (даже к 1629 году) вполне осмыслить новое понятие движения, привносимое законом сохранения движения, он всегда разделяет каузальное объяснение и математический анализ, развитие во времени и геометрическую репрезентацию свободного падения.

Мерсенн (не станем его корить за это) не вполне понял объяснение Декарта. Тогда последний вновь принимается за поставленную проблему281:

В вашем последнем письме, – пишет он Мерсенну, – вы спрашиваете, почему я говорю, что скорость сообщается [телу] тяжестью – как единичная в первый момент падения и как двойная во второй момент и т. д. Я отвечаю, при всем уважении, что я имел в виду вовсе не это, а то, что скорость сообщается тяжестью как единичная в первый момент и вновь сообщается той же тяжестью как единичная во второй момент и т. д. Однако единичная в первый момент и единичная во второй дают двойную, и единичная в третий дают тройную, и таким образом [скорость] возрастает в арифметической прогрессии. Тем не менее я полагал, что достаточно обосновал это, исходя из того, что тяжесть всегда сопровождает тела, в которых она присутствует; и она может сопровождать тело иначе, чем постоянно увлекая его вниз. Также если мы предположим, к примеру, что кусок свинца падает вниз благодаря силе тяжести и что с первого момента от начала падения Бог отбирает тяжесть у свинца таким образом, что после этого кусок свинца не более тяжел, чем если бы он был из воздуха или из перьев; этот кусок продолжал бы опускаться, особенно [если бы он находился] в пустоте, ведь он начал опускаться; и нельзя указать никакой причины, почему его скорость бы уменьшилась, а не возросла. Однако если через некоторое время Бог вернул бы этому куску свинца его тяжесть, причем лишь на мгновение, разве сила тяжести не тянула бы свинец [вниз] так же, как в первый момент? То же можно сказать о других моментах. Отсюда, безусловно, следует, что, если бы вы уронили мяч in spatio plane vacuo282 с высоты 50 футов, из какой бы материи он ни состоял, ему всегда будет требоваться ровно в три раза больше времени, чтобы пройти первые 25 футов, чем оставшиеся 25 футов. Но [нахождение] в воздухе – это совсем другое дело…

Это новое объяснение, по правде сказать, не прибавляет ничего нового к тому, что Декарт говорил Мерсенну в предыдущем письме. Отметим еще раз, насколько близка декартовская идея к теории импетуса: тяжесть – это вспомогательная причина, которая тянет тело вниз! Это идея Бенедетти в чистом виде283. Отметим также, что Декарт, кроме того, добавляет:

Следует помнить, что мы допустили, что тело, однажды приведенное в движение, в пустоте будет двигаться вечно, и я собираюсь доказать это в своем трактате;