Этюды о Галилее

Все эти изменения Галилей, конечно же, не доведет до конца: придется подождать появления Декарта и Ньютона. Однако мы видели, что уже в своих первых пизанских работах юный Галилей обнаруживает недостатки в рассуждениях Бенедетти, Кардано и Тартальи. Их учение целиком основывается на паралогизме или на двусмысленности. Утверждение, что постоянная причина может порождать изменчивый эффект, содержит противоречие. Падение тяжелого тела в архимедовом пространстве ни в коем случае не может быть движением, которое само по себе увеличивает свою скорость. Допустить это – значит допустить творение ex nihilo216. Постоянная причина не может произвести такой эффект, который был бы непостоянным. И если падающее тело действительно ускоряет свое движение до тех пор, пока не достигнет положенной ему скорости, так это потому, что в начале его движение замедлено.

Эта оригинальная теория, в которой читатель, конечно же, узнал идею Гиппарха217, увы, содержит противоречие; точнее, она несовместима с представлением о геометрическом пространстве, поскольку она с необходимостью предполагает идею стремления тела к некой цели, идею удаленности тела от его цели, что, стало быть, более не оставляет места для постоянной скорости свободного падения218.

Галилей предпринимает нечто иное. На этот раз, непосредственно опираясь на Архимеда, он пытается построить физическую теорию, используя термины или, если угодно, модель гидродинамики. Следуя примеру «древних», он оставляет в стороне качественное различие между «тяжелым» и «легким»: всякое движение отныне будет объясняться в терминах взаимодействия (количественный параметр) тела и среды, в которой он находится.

Другая попытка, предпринятая почти в то же время, была направлена на то, чтобы совместить законы движения с законами равновесия рычагов. Можно было бы назвать теорию, которую пытается построить Галилей, физикой жестких связей [liaisons rigides]219.

Мы не знаем, почему Галилей не стал далее продолжать попытки построить эту гидродинамическую теорию, так же как и не стал продолжать попытки основать физику жестких связей. Впрочем, возможно, было бы уместно предложить гипотезу: гидродинамическая физика, так же как и физика жестких связей, предполагает физическое пространство, не допуская при этом ни окончательной геометризации пространства, ни даже движения в пустоте. Однако движение в пустоте и геометризация пространства являются значимыми элементами галилеевской физики, они представляют для него важнейшее привнесение физики импетуса. Отказавшись от этой теории, Галилей всегда будет продолжать пользоваться ее плодами.

***

Стоит подчеркнуть первостепенную важность того, что Галилей отказался от идеи импетуса как внутренней причины движения тела. Конечно, он сохранит этот термин220, но его значение полностью изменится: из причины движения импетус превратится в его эффект. Что касается теории импетуса как причины движения, она просто-напросто исчезает. В представлении Галилея это «незаконнорожденное», запутанное, неясное понятие не нашло никакой замены или же (что одно и то же) его заменили на понятия скорости и движения. Еще в Пизе, изучая абстрактные и особые (простые) случаи движения, такие как круговое движение «вокруг центра», горизонтальное движение, предел между ускоряющимся движением падения и замедляющимся движением подъема, Галилей понял, что в этих случаях, вопреки самой сути теории импетуса, движение, казалось бы, может длиться бесконечно221. Сторонники теории импетуса (по крайней мере некоторые из них, в число которых входили Пикколомини и даже Буридан) утверждали, что в некоторых случаях, в частности в случае кругового движения, импетус вечен (неиссякаем). В таком случае, говорят они, импетус не противостоит никакому сопротивлению; но почему же тогда он ослабевает? В этом соображении, безусловно, можно распознать смутный намек на истину, однако Галилей не мог допустить подобное. Импетус, определяемый как причина движения, должен был – Галилей это прекрасно понимал – иссякать в процессе движения. Если бы он оставался равным самому себе, то лишь потому, что в продолжающемся движении он не играл бы никакой роли. Значит, это не импетус сохраняет движение и заставляет его длиться – оно само сохраняется. И коль скоро движение включает в себя скорость как свою сущностную характеристику, то утверждая, что движение само сохраняется таким, как оно есть, мы вместе с тем утверждаем, что и скорость также сохраняется. Движение, так же как и скорость – в особенности скорость, – некоторым образом сменяет свой онтологический статус: из эффектов, произведенных некой причиной, которые существуют и длятся, лишь, пока длится действие причины, которая их производит (например, давление), они становятся относительно независимыми сущностями, которые способны самосохраняться, подобно тому как сохраняется покой тела, которое не движется222. Это то, что касается «абстрактного» движения. Что до «конкретного» и «механического» движения, то это понятие Галилей разрабатывает в Падуе, и оно постепенно вырисовывается и высвобождается из беспорядочной магмы теории импетуса. Преподавая курс механики в Падуе, Галилей сформулировал понятие момента – произведения веса и скорости. Эта идея, по-видимому, уже была подготовлена автором «Quaestiones Mechanicae»223, а также авторами теории импетуса в их идее привходящей тяжести, которая, по их мнению, порождается самим движением груза, его скоростью, точнее его импетусом. Дюэм был прав, настаивая на этом факте. Тем не менее Дюэм не заметил решительного изменения, которое эта идея претерпела у Галилея224.

В действительности галилеевское понятие момента означает для движения (или скорости) то возвышение онтологического достоинства, о котором мы говорили: нет никакой необходимости ни в импетусе-причине, ни в каком-либо посреднике: движение непосредственно сопряжено с тяжестью. Короче говоря, движение или скорость просто-напросто замещает собой импетус. Очевидно, что такое замещение грозит очень серьезными последствиями: в самом деле, в то время как импетус, производя движение, не мог сохраняться и движение, следовательно, с необходимостью должно было утрачивать скорость и в конце концов достичь покоя, движение или скорость, удостоенные статуса независимых сущностей, вполне могут бесконечно сохраняться. Тело, однажды приведенное в движение, более не вынуждено останавливаться, ни даже уменьшать скорость своего движения. Тем самым было положено основание для правильного решения проблемы свободного падения.

***

Когда в 1604 году Галилей вновь возвращается к проблеме свободного падения тел, он располагает, как мы видели, формулами, в которых связываются длительность падения и пройденное расстояние; он располагает, как мы только что выяснили, важнейшим принципом сохранения движения и скорости. С другой стороны, он отказывается от всякой попытки каузального объяснения и ищет лишь принцип, аксиому, которая позволила бы вывести дескриптивные законы движения. Мы также видели, что рассмотрение движения (движения вообще и движения свободно падающего тела в частности) с точки зрения причин выводило понятие времени на первый план. Таким образом, неудивительно, что отказ от каузального объяснения подкрепляет тенденцию к геометрическому и, следовательно, к пространственному представлению движения. Вместо того чтобы мыслить движение, Галилей его представляет. Он видит линию – расстояние, пройденное с изменяющейся скоростью. Именно эту линию (траекторию) он принимает за аргумент функции скорости. Стремление к геометризации, подкрепленное работой воображения, не затрудненное каузальным мышлением, превосходит назначенную цель: целью динамики было математизировать время, а Галилей его [время] устраняет. Приложенные усилия привели к ошибке, которую Галилей сперва не замечает. Переворачивая порядок рассуждения, он выводит из правильных дескриптивных формул неправильный принцип, опираясь на который он приходит к верным заключениям, из которых исходил.

Вот, собственно, что он пишет225:

Я полагаю (и, вероятно, смогу это доказать), что тяжелое тело, падающее естественным образом, движется, непрерывно увеличивая свою скорость, сообразно тому как увеличивается расстояние от точки, от которой оно начало движение: так, например, если тело отправляется от точки А, падая вдоль линии АВ, я полагаю, что степень скорости в точке D будет настолько больше, чем степень скорости в точке С, насколько расстояние DA больше, чем CA, и таким образом степень скорости в Е относится к степени скорости в D как EA относится к DA, и таким образом в каждой точке линии АВ [тело] наделено степенями скорости, пропорциональными расстояниям от тех самых точек до пункта А. Этот принцип мне кажется очень естественным и отвечающим всякому опыту, наблюдаемому в приборах и машинах, работающих за счет толчков, где удар производит тем больший эффект, чем больше высота, с которой он обрушивается; и, предположив данный принцип, я докажу все прочее.

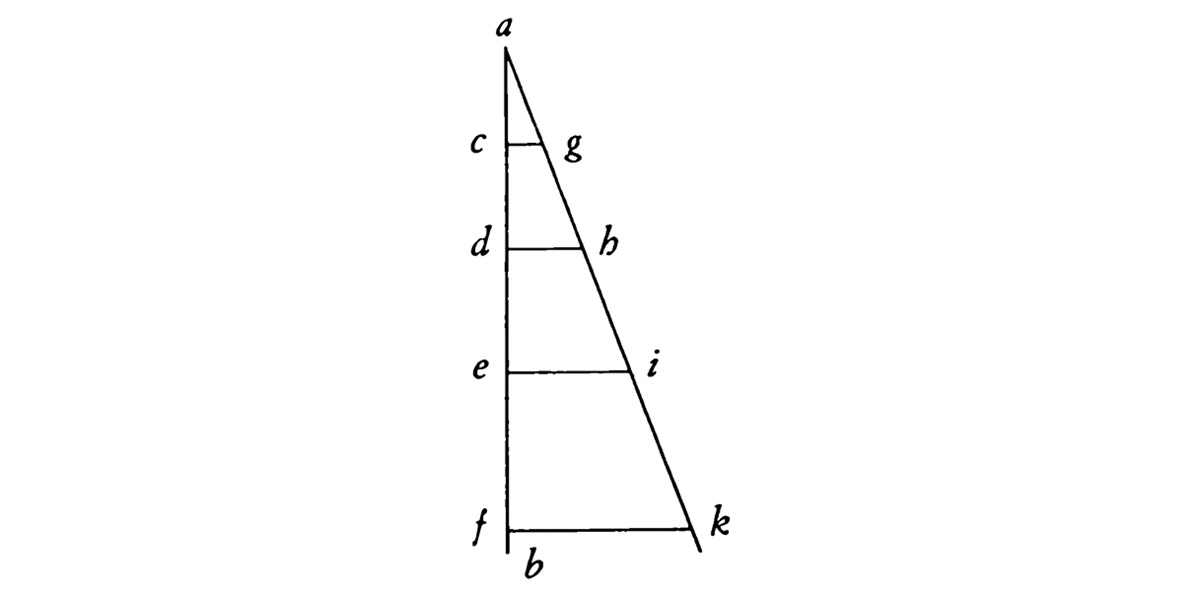
Пусть линия АК образует какой угодно угол с линией AF и от точек C, D, E, F отходят параллельные линии CG, DH, EI, FK; и так как линии FK, EI, DH, CG относятся между собой как FA, EA, DA, CA, то скорости в точках F, E, D, C относятся как отрезки FK, EI, DH, CG. Таким образом, степени скорости в каждой точке линии AF увеличиваются сообразно увеличению параллельных линий, проведенных из соответствующих точек. Кроме того, так как скорость, с которой предмет двигался, придя от точки А к точке D, составлена из всех степеней скорости, полученных во всех точках линии AD, и скорость, с которой предмет прошел линию AC, составлена из всех степеней скорости, которые он получил во всех точках AC, то скорость, с которой предмет прошел АD, относится к скорости, с которой он прошел АС, в такой пропорции, в какой относятся друг к другу все отрезки, проведенные из всех точек линии AD до линии AH, ко всем отрезкам, проведенным от всех точек линии АС до линии AG. И в этой пропорции треугольник ADH относится к треугольнику ACG, т. е. как квадрат AD относится к квадрату АС. Следовательно, скорость, с которой пройдена линия AD, относится к скорости, с которой пройдена линия АС, в удвоенном отношении DA к CA. И так как отношение одной скорости к другой обратно пропорционально отношению одного промежутка времени к другому (так как увеличивать скорость – это то же самое, что уменьшать время), следовательно, время движения в AD относится ко времени движения в AC в дважды разделенном отношении расстояния AD к расстоянию AC. Таким образом, расстояния от начала движения соотносятся как квадраты времени, и, следовательно, пройденные в равные промежутки времени расстояния соотносятся как нечетные числа, начиная от единицы, что соответствует тому, что я всегда утверждал, а также наблюдаемому опыту; и, таким образом, все истины согласуются. И если сказанное верно, то я доказываю, что скорость при насильственном движении уменьшается в той же пропорции, в которой она, проходя вдоль той же прямой линии, увеличивается при естественном движении226.

Рассуждение Галилея выглядит правдоподобно. И тем не менее оно ошибочно, поскольку, как легко можно увидеть, оно содержит двойную ошибку227. Справедливо, что отношение скоростей обратно отношению временных промежутков, при условии что основание для сравнения, т. е. пройденное расстояние, будет одинаковым, а не различным, как в нашем случае. Также совершенно справедливо и то, что конечная скорость предмета является суммой скоростей (мгновенных), которых он достигает в каждой точке своего пути; она также является суммой скоростей, достигнутых предметом в каждый момент его движения. Но эти «суммы» не подобны: постоянное и равномерное возрастание по отношению ко времени не будет таковым по отношению к расстоянию и наоборот, и, в частности, «суммы» скоростей, которые возрастают в линейной зависимости от пройденного расстояния, невозможно представить с помощью треугольников. Такое представление годилось бы только для равномерного возрастания по отношению ко времени. И вновь Галилей впадает в чрезмерную геометризацию и преобразует в пространство то, что относится ко времени.

Любопытно отметить, что Галилей обнаружит свою ошибку228 (ошибку в выборе принципа/определения ускоряющегося движения свободного падения), в то время как, вопреки утверждениям Дюэма, Декарт этого никогда не сделает. Еще более любопытно то, что рассуждение, с помощью которого Галилей пытается доказать абсурдность принципа, который сперва казался ему таким «естественным», совершенно ошибочно229.

Но, возможно, вовсе не это кажущееся правдоподобным (и предполагающее знание метода правильной дедукции) рассуждение движет мыслью Галилея. Более вероятно предположение, что его оплошность проявилась более непосредственным образом: в самом факте того, что принятый им «аксиоматический принцип» не мог играть той роли, которую он хотел ему приписать, из него было невозможно (что само собой разумеется) вывести дескриптивные формулы230. Также Галилей не смог бы правильно ее использовать. Вероятно, что этого было бы достаточно; вероятно, повторное исследование проблемы заставило Галилея обнаружить его ошибку. Без всякого сомнения, ошибка коренилась в пренебрежении «теснейшей связностью движения и времени»231. И, возможно, также в пренебрежении причинным фактором. Хвала, которую он впоследствии возносит идее притяжения, сформулированной Гильбертом232, восхищение, которое он всегда испытывал к великим английским физикам233, делают эту гипотезу вполне правдоподобной234: падающее тело ускоряет свое движение, потому что в каждый последующий момент оно претерпевает одно и то же мгновенное действие – притяжение Земли. И формула (сущностное определение) ускоряющегося движения должна брать за основу не пространство, а время.

2. Декарт

Обратимся же теперь к Декарту.

В 1618 году Исаак Бекман случайно познакомился с г-ном дю Перроном. Вскоре Бекман открыл необычайные дарования, которыми природа наделила молодого француза235. Потому он обратится к Декарту за помощью в разрешении сложнейшей проблемы ускоряющегося движения падающих тел.

История сотрудничества Бекмана и Декарта была настоящей комедией ошибок и пересказывалась уже не раз236. Тем не менее мы полагаем, что имеет смысл остановиться на ней снова.

Бекман не спрашивает Декарта, почему тела падают вообще: ответ на этот вопрос он знает. Вероятно, он узнал об этом у Гильберта237или у Кеплера. Тела падают, потому что Земля их притягивает. Он также не спрашивает, почему они ускоряются: это ему также известно. Тела ускоряются при падении, потому что в каждый момент движения они вновь притягиваются Землей, и эти новые силы притяжения в каждый момент времени сообщают телам новую степень движения, в то время как движение, которое их охватывало ранее, продолжает сохраняться. Еще в 1613 году Бекман сформулировал важное положение: то, что однажды было приведено в движение, вечно остается в движении, – уже тогда ему был известен закон сохранения движения238.

Все это (а это немало) составляет всю физическую суть данной проблемы239, и, стало быть, Бекману она была известна еще до встречи с Декартом; но прекрасно понимая (гораздо лучше, чем ее понимал Декарт) физическую сторону вопроса, он оказывается не способен осилить его математический аспект. Он не может вывести следствия из принципов, которыми он располагает; он не может найти формулу, позволяющую рассчитать скорость тела и пройденный им путь240.

Именно об этом он спрашивает Декарта.

Итак, он задает ему вопрос241:

Допустив установленные мной принципы, а именно что то, что приведено в движение, в пустоте движется вечно, и предположив существование пустоты между землей и падающим камнем, можно ли узнать расстояние, которое падающее тело пройдет за час, если известно, сколько оно прошло за два часа?

Формулировка вопроса необычна. Бекман не спрашивает, как казалось бы естественным спросить, можно ли узнать, какое расстояние пройдет падающее тело за два часа, если известно, сколько оно прошло только за один час. Мы видим, что он ставит вопрос иначе.

Ясно, что Бекман, рассматривающий свободное падение уже не как «естественное» движение, а как эффект земного притяжения, распространяющегося на падающее тело, которое само по себе не испытывает никакой склонности двигаться в том или ином направлении и, более того, двигаться вообще (тело, естественно, остается в покое, если его не приводит в движение какая-нибудь внешняя сила, тогда оно остается в этом новом состоянии – в состоянии движения, подобно тому как оно оставалось в покое), может мыслить свободное падение не иначе как движение, имеющее естественную, установленную цель (землю), а не как, подобно Бенедетти или юному Галилею, движение, способное длиться неограниченно242. Поэтому он представляет себе свободное падение тела как движение, проходящее от точки А до точки В: от вершины башни или от какой-либо точки, расположенной над землей, до земли. Именно это движение – «подытоженное» – мы можем измерить – т. е. измерить пройденное расстояние и потребовавшееся время. Именно от этого мы должны отталкиваться, чтобы воссоздать с помощью анализа предшествующие фазы243.

Это не совсем то, каким образом движение свободного падения будет рассматривать Декарт. Потому его ответ будет неточным. Однако Бекман этого не разглядит.

Действительно, вот что, согласно Бекману, Декарт ответил на вопрос «почему в пустоте камень всегда падает с большей скоростью», «исходя из принципов», установленных Бекманом244:

Если между телом и Землей пустота, тело движется вниз, к центру Земли, следующим образом: в первый момент времени оно проходит такое расстояние, которое оно может пройти вследствие земной тяги245; во второй момент оно продолжает пребывать в этом движении, к которому прибавляется новое движение тяги, таким образом, что за один этот момент времени оно проходит двойное расстояние. В третий момент времени двойное расстояние удерживается246 и вследствие земной тяги к нему прибавляется третье, таким образом, что в один момент тело проходит тройное расстояние по отношению к пройденному в первый момент времени.

Эти соображения, которые, как мы вскоре увидим, представляют собой бекмановскую трактовку рассуждений Декарта, позволяют правильно разрешить поставленную проблему и рассчитать время свободного падения тела. Последуем же далее за изложением Бекмана247:

Но так как эти моменты неотделимы друг от друга, расстояние, которое проходит тело в своем падении за час, будет равно ADE. Расстояние, которое оно пройдет за два часа (падая), удваивает пропорцию по времени, т. е. как ADE к ACB, что является двойной пропорцией AD к AC. Пусть момент расстояния, которое тело проходит при падении за один час, будет какой угодно величины, например ADEF. За два часа оно пересечет три одинаковых момента, т. е. AFEGBHCD. Но AFED составлено из ADE и AFE. И AFEGBHCD составлено из ACB с AFE и EGB, т. е. из удвоенного AFE.

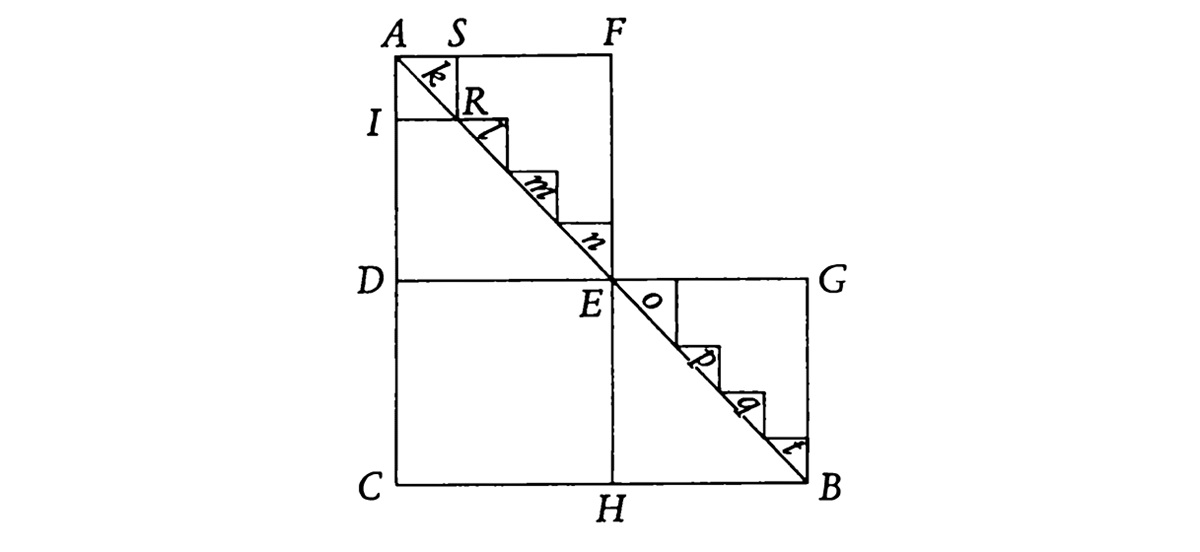
Так, если момент времени равен AIRS, то отношение расстояний будет равно ADЕ c klmn к ACB с klmnopqt – т. е. опять же с удвоенным klmn. Но klmn гораздо меньше, чем AFE. Следовательно, так как отношение проходимого расстояния к пройденному расстоянию составлено из отношения одного треугольника к другому, и к таким условиям [пропорции] прибавляются равные [величины], и так как эти равные присоединенные части становятся тем меньше, чем меньше единицы расстояния, отсюда следует, что эти присоединенные части оказываются нулевой величины, когда величина момента равна нулю. Таков момент расстояния падающего тела. Остается теперь доказать, что расстояние, которое проходит падающее тело за один час, относится к расстоянию, которое оно проходит, падая два часа, как треугольник ADE к треугольнику ACB…

Если, стало быть, опыт показал бы, что тело, падая два часа, проходит 1000 футов, то треугольник АВС будет содержать 1000 футов248. Отсюда корень составляет 100 для линии АС, которая соответствует двум часам. Поделив ее точкой D на равные части, получим AD, соответствующую одному часу. Каким получается двойное отношение AC к AD, т. е. 4 к 1, получается также отношение 1000 к 250, т. е. ACB к ADE.

Решение одновременно изящное и правильное: пройденные расстояния оказываются пропорциональны квадратам времени. Но решение Декарта не таково: Бекман, как известно, ошибся, интерпретируя ответ г-на дю Перрона249. В самом деле, вот переизложение, которое нам оставил сам Декарт.

В своих «Cogitationes Privatae» Декарт кратко отмечает250:

Несколько дней назад мне довелось завязать дружбу с одним весьма ученым мужем, который задал мне следующий вопрос:

Камень, говорил он, нисходит от точки А к точке В в течение одного часа; он неизменно притягивается Землей с одинаковой силой и не теряет скорости, которая была ему сообщена через предыдущее притягивание. Но то, что движется в пустоте, по его мнению, движется вечно. Спрашивается, за какое время камень пройдет заданное расстояние.

Отметим прежде всего, что Декарт признавал, что получил от Бекмана и вопрос, и принципы решения251 – принципы, которые не имеют для него истинного значения, в отличие от Бекмана. Для Декарта они не более чем гипотезы, которые он, впрочем, не вполне понимает. Это не мешает ему разрешить данную проблему и даже предложить два различных решения. Бедный Бекман о таком и не просил, он лишь хотел узнать, как падают камни. Декарт этим не удовлетворился и объяснил ему, как они могли бы падать252.

Итак, вот его ответ253:

Я решил задачу. Площадь равнобедренного прямоугольного треугольника АВС представляет расстояние (движение); неравенство расстояния от точки А до основания ВС – неравенство движения254. Как следствие, AD будет пройдено за время, которое представлено ADE, и DB – за время, представленное DEBC: следует отметить, что меньшая площадь представляет более медленное движение. Но ADE составляет третью часть DEBC, а значит, AD будет пройдено в три раза медленнее, чем DB.

Но этот вопрос можно было бы поставить и иначе, именно: [допустим,] что сила притяжения Земли равна силе, которую оно производило в первый момент, и что новая производится, тогда как предыдущая продолжает существовать. В таком случае проблема разрешалась бы при помощи пирамиды.

Любопытное дополнение! Совершенно ясно, до чего проблема физического механизма свободного падения чужда мышлению Декарта. Его отнюдь не останавливает то, что у Бекмана уже есть решение. И он воображает иной «возможный» случай, в котором сила притяжения возрастала бы с каждым мигом – так, что во второй момент тело притягивалось бы с удвоенной силой, в третий – с тройной силой и т. д. В таком случае, разумеется, тела бы падали куда быстрее255.

Как могло бы быть возможным подобное возрастание «силы притяжения»? Декарт не задается этим вопросом. В действительности он рассматривает проблему не как физик, а как чистый математик, чистый геометр: для него задача заключается в том, чтобы установить соотношение между двумя последовательностями переменных величин. Почему бы, раз уж представился случай, не проверить забавную гипотезу?

Декарт – геометр, чистый математик. Именно в этом, видимо, заключается причина, по которой он не вполне понял «принципы» Бекмана и дал ошибочный ответ на его вопрос. Он видит проблему, как и сам исследуемый феномен, совершенно иначе, чем Бекман.

Так же как и Бекман, он исходит из завершившегося движения свободного падения. Но в отличие от него, Декарт видит это движение в некотором смысле «приостановленным». Или, если угодно, он рассматривает лишь траекторию свободного падения тела, или, если угодно, сформулируем это иначе – он инстинктивно элиминирует время.

Для Декарта линия ADB, которая для Бекмана представляла затраченное время256, естественным образом представляет пройденный путь. И проблема видоизменяется: путь пройден с «равномерно изменяющейся» скоростью; проблема, таким образом, заключается в том, чтобы определить скорость в каждой точке пути. Треугольники ADE, ABC, которые у Бекмана представляли пройденное расстояние (траекторию), у Декарта представляют движение предмета, т. е. «сумму скоростей», которые были достигнуты. И он делает весьма правдоподобное заключение: если «сумма скоростей» утраивается, то расстояние DB будет пройдено в три раза быстрее. Время отыскивается, но слишком поздно: крайняя геометризация, пространственное представление, элиминация времени (там, где его нельзя элиминировать), пренебрежение физическим, каузальным аспектом этого процесса – все это приводит Декарта, как когда-то привело Галилея, а до него – Бенедетти и Мишеля Варрона, к тому, что он мыслит равномерно ускоряющееся движение как движение, скорость которого возрастает пропорционально пройденному пути, а не пропорционально затраченному времени.