Этюды о Галилее

220

Ньютон также его использует.

221

См. выше, I и далее.

222

Таким образом, покой и движение станут состояниями и будут обладать равной онтологической значимостью. Так, для Аристотеля и для схоластов покой есть не что иное, как лишенность, в то время как движение – это процесс. Из этого следует, что покой длится без всякой причины (лишенность не нуждается в причине, чтобы длиться), в то время как движение существует лишь в качестве эффекта причины, которая его поддерживает. Также к нему применим принцип cessante causa cessat effectus [при прекращении действия причины прекращается эффект (лат.)].

223

[Псевдо-Аристотель.] Quaestiones Mechanicae. II. 24.

224

Сохранение терминологии (Ньютон все еще говорит об импетусе) сбило с толку Дюэма, который упустил из виду, какое существенное изменение это понятие или этот термин претерпел у Галилея. Именно этим недоразумением объясняются (но не оправдываются) подобные суждения, где каждое слово ошибочно (Duhem P. De l’accélération… P. 888): «…рискуя исказить полученные представления и неверно пересказать легенды, мы должны утвердить следующие положения: взгляд, который исповедуется Галилеем на предмет динамики, несет глубокий отпечаток перипатетических принципов; они мало в чем расходятся с учениями, принимаемыми большинством физиков XVI века: они существенно отстают от представлений некоторых из их предшественников». Не более обоснованны аналогичные суждения, высказанные в: Duhem P. Les origines de la statique. Vol. I. Paris, 1905. P. 260 sq.; Études sur Léonard de Vinci. Vol. III. P. 560 sq.

225

Galileo G. Frammenti attenenti ai Discorsi… // Le opere. Vol. VIII. P. 373: «Io suppongo (et forse potró dimostrarlo) che il grave cadente naturalmente vada continuamente accrescendo la sua velocità secondo che accresce la distanza dal termine onde si partì: come, v. g., partendosi il grave dal punto a et cadendo per la linea ab, suppongo che il grado di velocità nel punto d sia tanto maggiore che il grado di velocità in c, quanto la distanza da è maggiore della ca, et così il grado di velocità in e esser al grado di velocità in d come ea a da, et così in ogni punto della linea ab trovarsi con gradi di velocità proporzionali alle distanze dei medesimi punti dal termine a. Questo principio mi par molto naturale, et che risponda a tutte le esperienze che veggiamo negli strumenti et machine che operano percotendo, dove il percuziente fa tanto maggiore effetto quanto da più grande altezza casca: et supposto questo principio dimostreró il resto.

Faccia la linea ak qualunque angolo con la af, et per li punti c, d, e, f, siano tirate le parallele cg, dh, ei, fk: et perchè le linee fk, ei, dh, cg sono tra di loro come le fa, ea, da, ca, adunque le velocità ne i punti f, e, d, c sono come le linee fk, ei, dh, cg. Vanno dunque continuatamente crescendo i gradi di velocità in tutti i punti della linea af secondo l’incremento delle parallele tirate da tutti i medesimi punti. In oltre, perchè la velocità con la quale il mobile è venuto da a in d è composta di tutti i gradi di velocità hauti in tutti i punti della linea ad, et la velocità con che ha passata la linea ac è composta di tutti i gradi di velocità che ha auti in tutti i punti della linea ac, adunque la velocità con che ha passata la linea ad, alla velocità con che ha passata la linea ac, ha quella proportione che hanno tutte linee parallele tirate da tutti i punti della linea ad sino alla ah, a tutte le parallele tirate da tutti i punti della linea ac sino alla ag; et questa proportione è quella che ha il triangolo adh al triangolo acg, ció è il [quadrat]o ad al [quadrat]o ac. Adunque la velocità con che si è passata la linea ad, alla velocità con che si è passata la linea ac, ha doppia proporzione di quella che ha da a ca. Et perchè la velocità alla velocità ha contraria proporzione di quella che ha il tempo al tempo (imperó che il medesimo è crescere la velocità che sciemare il tempo), adunque il tempo del moto in ad al tempo del moto in ac ha subduplicata proporzione di quella che ha la distanza ad alla distanza ac. Le distanze dunque dal principio del moto sono come i quadrati de i tempi, et, dividendo, gli spazii passati in tempi eguali sono come i numeri impari ab unitate: che risponde a quello che ho sempre detto et con esperienze osservato; et così tutti i veri si rispondono.

Et se queste cose son vere, io dimostro che la velocità nel moto violento va decrescendo con la medesima proporzione con la quale, nella medesima linea retta, cresce nel moto naturale. Imperó che sia il principio del moto violento il punto b, et il fine il termine a. Et per che il proietto non passa il termine a, adunque l’impeto che ha hauto in b fu tanto, quanto poteva cacciarlo sino al termine a; et l’impeto che il medesimo proietto ha in f è tanto quanto puó cacciarlo al medesimo termine a; et sendo il medesimo proietto in e, d, c, si trova congiunto con impeti potenti a spingerlo al medesimo termine a, nè più nè meno: adunque l’impeto va giustamente calando secondo che sciema la distanza del mobile dal termine a. Ma secondo la medesima delle distanze dal termine a va crescendo la velocità quando il medesimo grave caderà dal punto a, come di sopra si è supposto et confrontato con le altre prime nostre osservazioni et dimostrazioni: adunque è manifesto quello che volevamo provare». См. также p. 380 и 383: «Assumo, eam esse cadentis mobilis per lineam al accelerationem, ut pro ratione spacii peracti crescat velocitas ita, ut velocitas in c ad velocitatem in b sit ut spacium ca ad spacium ba, etc. Cum autem haec ita se habeant, ponatur ax cum al angulum continens, sumptisque partibus ab, bc, cd, de etc. aequalibus, protrahantur bm, cn, do, ep etc. Si itaque cadentis per al velocitates in b, c, d, e locis se habent ut distantiae ab, ac, ad, ae etc., ergo se quoque habebunt ut lineae bm, cn, do, ep. Si itaque eadentis per al velocilates in b, c, d, c, locis se habent ut distantiae ab, ac, ad, ae, etc., ergo se quoque habebunt ut lineae bm, en, do, ep.

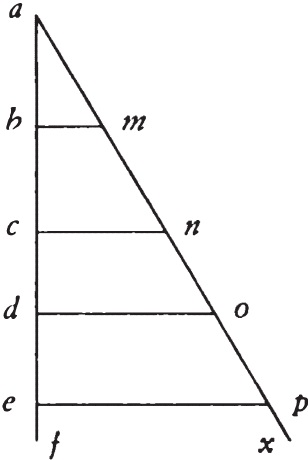
Quia vero velocitas augetur consequenter in omnibus punctis lineae ae, et non tantum in adnotatis b, c, d, ergo velocitates illae omnes sese respicient ut lineae quae ab omnibus dictis punctis lineae ae ipsis bm, cn, do aequidistanter producuntur. Istae autem infinitae sunt, et constituunt triangulum aep: ergo velocitates in omnibus punctis lineae ab ad velocitates in omnibus punctis lineae ac ita se habent ut triangulus abm ad triangulum acn, et sic de reliquis, hoc est in duplicata proportione linearum ab, ac.

Quia vero pro ratione incrementi accelerationis tempora quibus motus ipsi fiunt debent imminui, ergo tempus quo mobile permeat ab ad tempus quo permeat ac erit ut ab linea ad eam quae inter ab, ac media proportionalis existit».

226

И далее: «Положим [теперь], что начало насильственного движения – в точке В и оно завершается в точке А. И так как брошенное тело не идет дальше точки А, то, следовательно, импетус, полученный им в точке В, был таков, что он мог продвинуть тело вплоть до точки А. Импетус, который это же тело имеет в точке F, таков, что может продвинуть его до той же точки А. И когда это тело оказывается в точках E, D, C, оно будет соединено с импетусами, способными протолкнуть его к той же точке А – не больше и не меньше: следовательно, импетус действительно движется, ослабевая по мере того, как сокращается расстояние до точки А. Но когда то же самое тело падает от точки A, то движется с возрастающей скоростью сообразно тому же самому соотношению расстояния до точки А, как ранее предполагалось и показывалось прочими более ранними нашими наблюдениями и доказательствами. Таким образом, очевидно то, что мы хотели доказать».

227

См.: Duhem P. Études sur Léonard de Vinci. Vol. III. P. 570 sq.

228

Вот рассуждение Галилея (см.: Discorsi e dimostrazioni matematiche… // Le opere. Vol. VIII. P. 204; рус. пер.: Галилей Г. Избранные труды: В 2 т. Т. 2. С. 245), на заключение которого ссылаются Дюэм (Op. cit. P. 578) и Каверни (Caverni R. Storia del metodo sperimentale in Italia. Vol. IV. Bologna, 1895. P. 295): «Если бы скорости были пропорциональны пройденным или имеющим быть пройденными расстояниям, то такие расстояния проходились бы в равные промежутки времени; таким образом, если бы скорость, с которою падающее тело проходит расстояние в четыре локтя, была вдвое больше скорости, с которою оно проходит расстояние в два первых локтя (на том основании, что одно расстояние вдвое больше другого), то промежутки времени для прохождения того и другого расстояния должны были бы быть одинаковыми. Но прохождение одним и тем же телом четырех локтей и двух локтей в один и тот же промежуток времени могло бы иметь место лишь в том случае, если бы движение происходило мгновенно; мы же видим, что падающее тело совершает свое движение во времени и что два локтя оно проходит в меньший срок, нежели четыре локтя. Следовательно, утверждение, что скорости растут пропорционально пройденным путям, ложно». Это рассуждение содержит ошибку, аналогичную той, что допускается в рассуждении, о котором мы говорили чуть выше: Галилей применяет здесь к движению, скорость которого возрастает пропорционально пройденному расстоянию, вычисление, которое пригодно только для равномерно ускоряющегося движения (в отношении ко времени). См.: Mach E. Die Mechanik in ihrer Entwicklung. Leipzig, 1912. S. 245, и Tannery P. Mémoires scientifiques. Vol. VI. Paris, 1926. P. 400 sq.

229

Правильный вывод приведет Галилея к формулам, открытым Декартом.

230

На самом деле это была бы формула экспоненциальной функции.

231

Выражение, использованное Галилеем.

232

См. ниже, III.

233

Тем не менее Галилей никогда не примет теории Гильберта и никогда не будет пытаться использовать гильбертово понятие притяжения для формулировки теории свободного падения тел. Это можно легко объяснить: физика Гильберта анимистична; до Ньютона ни один ученый (даже Кеплер) не сумеет описать притяжение математически.

234

См.: Duhem P. De l’accélération… P. 907.

235

Впрочем, Декарт не утаивал своих талантов. См.: Журнал Исаака Бекмана. AT X. P. 331.

236

См. главным образом: Duhem P. Études sur Léonard de Vinci. Vol. III: Les Précurseurs Parisiens de Galilée. Paris, 1913. P. 566 sq., и Milhaud G. Descartes savant. Paris, 1920. P. 25 sq. См. также: Sirven J. Les années d’apprentissage de Descartes. Paris, 1928.

237

Работа Гильберта (Gilberti G. C. De Magnete. Лондон, 1600), в которой Земля превращается в магнит и свободное падение объясняется земным притяжением, имела широкий резонанс и сыграла первостепенную роль в развитии и преобразовании физических теорий. Ее также очень высоко оценивал Галилей, вслед за ним и Кеплер, Гассенди и Ньютон. Вероятно, созданная Гильбертом идея притяжения как некой чудесной силы, сравнимой с душой, была чужда духу новой науки и тем самым оказалась бесполезной для Галилея и Декарта. Но именно сюда будут устремлены усилия Гассенди и Ньютона – на преобразование гильбертова притяжения в силу, не направленную на предмет.

238

Журнал Исаака Бекмана, 1613 (AT X. P. 60, примеч. f): «Mota semel nunquam quiescunt, nisi impediantur. – Omnis res semel mota nunquain quiescit, nisi propter externum impedimentuin. Quoque impedimentum est imbecillius, eo diutius mota movetur: si enim aliquid in altum projiciatur simulque circulariter moveatur, ad sensuin non quiescet ante reditum in terram; et si quiescat tandem id non fit propter impedimentum aequabile, sed propter impedimentum inaequabile, quia alia atque alia pars aeris vicissim rem motam tangit». Не будем же путать, однако, как делает Бекман куда более часто, чем это делал, например, Дюэм (см.: Duhem P. De l’accélération… P. 904) и до него Вольвиль, закон сохранения движения с законом инерции. Закон инерции подразумевает устойчивость движения по прямой; закон сохранения движения ничего подобного не подразумевает. Также Бекман верит в сохранение кругового движения, и он объясняет устойчивость движения планет через движение, которое легко можно наблюдать, – движение подвешенного на веревке канделябра, поскольку он полагает, что закон сохранения применим к движению вообще (АТ X. P. 225): «eo modo quo in recto motu valeat hoc theorema: quod semel movetur semper eo modo movetur dum ab extrinseco impediatur. In vacuo vero nulla tales consideratio habenda; magnum enim corpus, parvum, grave, leve, magna aut parva superficie, hac sive illa figura, etc. semper eo modo quo semel motum est, pergit moveri, his accidentibus nihil impedimenti alterentibus. Praeterea cum candelabra eo modo moventur quo dico annuum motum terrae fieri, si abscisso fune fieri posse, ut candelabra in aere elevata manerent neque deciderent, sed ut astra in caelo, sic haec in aere vagarentur, nulla ratio videtur esse cur non pergerent circulariter moveri, usque dum sacpius aeri occursando impcdita». Случай Бекмана не единственный: Гоббс также будет верить в устойчивость кругового движения; так, ни ему, ни даже Галилею, но лишь Декарту достанется слава быть первым, кто вполне ясно представил и сформулировал закон инерции.

Эти строки были написаны и даже напечатаны, когда Корнелис де Ваард переопубликовал фрагменты журнала Бекмана (Correspondance du P. Marin Mersenne / Paul Tannery (éd.) par Cornélis de Waard. Vol. II. Paris, 1936. P. 118 sq., 123 sq., 235 sq., 280 sq., etc.), ощутимо изменив представление, которое сложилось (точнее, которое не сложилось) о голландских физиках, и заставил нас горько пожалеть о том, что его замечательный журнал оставался неопубликованным. В самом деле, Бекман – теперь это ясно – в полной мере заслуживает титула vir ingeniosissimus, которым наделили Декарта; и, более того, отныне он предстал для нас как звено первостепенной значимости в истории эволюции научных идей; наконец, его влияние на Декарта, по-видимому, было куда более глубоким, чем до сих пор можно было предполагать; в частности, многие законы движения и передачи движения, сформулированные Декартом в «Первоначалах философии», имеют в качестве образца законы, установленные Бекманом (см.: Correspondance du P. Mersenne. Vol. II. App. I. A. P. 633 sq.); кроме того, эрудированный и прекрасно разбирающийся в научной литературе того времени, он, конечно же, передал Декарту знание о работах, которые тот не читал сам.

Бекман принадлежал к философскому течению, которое можно определить как брунианско-гильбертианское. Подобно Бруно, он допускает бесконечность Вселенной и бесконечное число неподвижных звезд; он также допускает существование пустоты, которую он приравнивает к эфиру и тонкой материи; подобно Гильберту и Кеплеру, именно в эфире он видит источник действия и притяжения; задолго до Декарта и Паскаля он объясняет, что жидкость поднимается в закрытых пробирках благодаря атмосферному давлению; еще до Декарта он формулирует принцип сохранения движения и отказывается от понятия импетуса, найдя правильное решение проблемы движения снаряда. Так, в 1620 году он заявляет, что «motus a Deo semel creatus non minus quam corporeitas ipsa in aeternum conservatur», и если, не зная, как объяснить с этой точки зрения неоспоримый факт остановки (стало быть, устранения движения) при столкновении неупругих тел, он пишет (Correspondance du P. Mersenne. Vol. II. P. 123): «Hic ita positis, nunquam motus in vacuo potest intelligi ad celeriorem motum vergere, sed omnia tandem spectare ad quietem propter aequales occursus. Unde sequitur Deum opt. max. solum potuisse motum conservare movendo semel maxima corpora minima celeritate, quae deinceps reliqua ad quietem semprem spectantia perpetuo resuscitant vivificant», то в 1629 году он утверждает, что такое устранение не что иное, как видимость, и что движение сохраняется, распределяясь между частями и атомами, из которых составлены тела (см.: Ibid. P. 236 sq.). – В 1614 году он критикует идею импетуса (Ibid. P. 236): «Lapis, projectus in vacuo, perpetuo movetur; obstat autem ei aer, qui novus semper ei occurit atque ita efficit ut motus ejus minuatur. Quod vero philosophi dicunt vim lapidi imprimi, absque ratione videtur; quis nempe posse concipere, quid sit illa aut quomodo lapidem in moto contineat, quave in parte lapidis sedem figat? Facillime autem mente quis cincipiat in vacuo motun nunquam quiescere, quia nulla causa mutans motum, occurit; nihil enim mutatur absque aliqua causa mutationis», и в 1618 году в Короллариях тезисов, которые он защищал в Кане, он заявляет (Ibid. P. 237): «Lapis e manu emissus pergit moveri non propter vim aliquam ipsi accedentem, nec ab fugam vacui, sed quia non potest non perseverare in eo moto, quo in ipsa manu existens movebatur». – Заслуга Бекмана, как мы видим, огромна. Не будем тем не менее ее преувеличивать и приписывать ему, как это делает его ученый издатель, открытие принципа инерции (см.: Ibid. P. 122, 236, 272). Ибо когда Корнелис де Ваард пишет (p. 236): «в первой из этих записей он лишь по ошибке применяет его [принцип инерции] к движению небесному и круговому, но спустя недолгое время (июль 1613 – апрель 1614) он распространяет его [только] на прямолинейное движение: «Omnis res semel mota, nunquam quiescit nisi propter externum impedimentum: quoque impedimentum est imbecillus, eo diutius mota movetur…», он просто-напросто совершает ту же ошибку, что и сам Бекман, который утверждает (Ibid. P. 360) «Id quod semel moventur in vacuo, semper moventur, sive secundum lineam rectam seu circularem tam super centro suo, qualis est motus diurnus Terrae et annuus», не замечая – что мы ни в коем случае не ставим ему в упрек, – что сохранение кругового и прямолинейного движения строго несовместимы.

239

Пришлось ждать по крайней мере тридцать лет до «De motu impresso a motore translato» Гассенди (Paris, 1643) – и дольше! – чтобы найти настольно ясное представление механизма свободного падения. Мы особо выделяем заслуги Бекмана, поскольку считаем, что ими уж слишком пренебрегли.

240

Это, между прочим, опровергает позицию Дюэма в отношении широкого распространения формулы или правила Орема в XVI–XVII веках (см.: Duhem P. Études sur Léonard de Vinci. Vol. III. P. 580 sq. et passim). У нас, напротив, создалось впечатление, что это правило было довольно мало известным.

241

См.: Descartes R. et Beeckman I. Physico-mathematica. AT X. P. 75 sq.

242

Любопытно, что концепция Бекмана, в целом очень естественная для коперниканца и совершившая заметный прогресс по сравнению с идеями Бенедетти и молодого Галилея, с другой стороны, очень близка традиционным представлениям о свободном падении как движении, направленном к цели.

243

Как мы уже могли видеть и увидим вновь, Галилей рассуждает иначе. Он всегда исходит из архимедовой концепции движения и исследует движение свободного падения как определенный вид движения вообще. Он не исходит из частного случая.

244

См.: Журнал Исаака Бекмана (AT X. P. 58): «Lapis cadens in vacuo cur semper celerius cadat: Moventur res deorsum ad centrum terrae, vacuo intermedio spatio existente, hoc pacto; Primo momento, tantum spacium conficit, quantum per terrae tractionem fieri potest. Secundo, in hoc motu perseverando superadditur motus novus tractionis, ita ut duplex spacium secundo momento peragretur. Tertio momento, duplex spacium perseverat, cui superadditur ex tractione terrae tertium ut uno momento triplum spacii primi peragretur».

245

Этот фрагмент чрезвычайно важен, поскольку в нем хорошо раскрывается вся разница между понятием притяжения и понятием склонности: притяжение действует извне, оно тянет тело к земле. Таким образом, движение свободного падения – horribile dictu – это насильственное движение. По-видимому, Кеплер, приводя взаимное притягивание, приводит ситуацию, вызывающую куда меньше вопросов; однако Декарт будет решительно приравнивать естественное движение свободного падения к насильственному движению, произведенному ударом.

246

«Двойное расстояние удерживается» – duplex spatium perseverat – сохраняется двойная скорость – т. е. то, что позволяет за этот момент времени пройти двойное расстояние.

247

Журнал Исаака Бекмана (AT X. P. 58 sq.): «Lapis cadentis tempus supputatum: Cum autem momenta haec sint individua, habebit spacium per quod res una hora cadit ADE. Spatium per quod duabus horis cadit, duplicat proportionem temporis, id est ADE ad ACB, quae est duplicata proportio AD ad AC. Sit enim momentum spatij per quod res una hora cadit alicujus magnitudinis, videlicet ADEF. Duabus horis perficiet talia tria momenta, scilicet AFEGBHCD. Sed AFED constat ex ADE cum AFE; atque AFEGBHCD constat ex ACB cum AFE et EGB id est cum duplo AFE. Sic si momentum sit AIRS, erit proportio spatii ad spatium, ut ADE cum klmn, ad ACB cum klmnopqt, id est etiam duplum klmn. Ast klmn est multo minus quam AFE. Cum igitur proportio spatii peragrati ad spatium peragratum constet ex proportione trianguli ad triangulum, adjectis utrique termino aequalibus, cumque haec aequalia adjecta semper eo minora fiant quo momenta spatii minora sunt: sequitur haec adjecta nullius quantitatis fore quando momentum nullius quantitatis statuitur. Tale autem momentum est spatii per quod res cadit. Restat igitur spatium per quod res cadit una hora se habere ad spatium per quod cadit duabus horis, ut triangulum ADE ad triangulum ACB. Haec ita demonstravit M. Perron, cum ei ansam praebuissem, rogando an possit quis scire quantum spatium res cadendo conficeret unica hora, cum scitur quantum conficiat duabus horis, secundum mea fundamenta, viz. quod semel movetur, semper movetur, in vacuo et supponendo inter terram et lapidem cadentern esse vacuum. Si igitur experientia compertum sit, lapidem cecidisse duabus horis per mille pedes, continebit triangulum ABC1000 pedes. Hujus radix est 100 pro linea AC quae respondit horis duabus. Bisecata ea in D, respondet AD uni horae. Ut igitur se habet proportio AC ad AD duplicata, id est 4 ad 1, sic 1000 ad 250, id est ACB ad ADE».

248

Отметим между прочим, что, так же как и Галилей, Декарт представляет расстояние, пройденное падающим телом, не через прямую линию, а через площадь. Дело в том, что ни Галилей, ни Декарт не думали в первую очередь о пройденном расстоянии; они думали о совершенном движении. Неделимый «момент», о котором говорит Декарт, это не «мгновение» – это ровно то же самое, что «степень скорости», о которой говорит Галилей; это мгновенное движение или скорость, минимум или, если угодно, дифференциал движения. Движение как таковое с необходимостью имеет два измерения. Также фигура (треугольник или прямоугольник) буквально представляет сумму бесконечных «моментов» или «степеней скорости». Это то, чего, как нам кажется, Дюэм так и не понял.