Этюды о Галилее

249

См.: Duhem P. Études sur Léonard de Vinci. Vol. III. P. 570, и Milhaud G. Descartes savant. Paris, 1920. P. 27.

250

Descartes R. Cogitationes Privatae. AT X. P. 219 sq. (рус. пер.: Декарт Р. Частные мысли // Сочинения: В 2 т. Т. 1. С. 576): «Contigit mihi ante paucos dies familiaritate uti ingeniosissimi viri, qui talem mihi quaestionem proposuit: Lapis, aiebat, descendit ab A ad B na hora; attrahitur autem a terra perpetuo eadem vit, nec quid deperdit ab illa celeritate quae illi impressa est priori attractione. Quod emin in vacuo movetur semper moveri existimabat. Queritur quo tempore tale spatium percurrat».

251

Известно, что Декарт впоследствии будет отрицать, что Бекман когда-либо чему-то его научил. См. письмо Мерсенну от 4 ноября 1630 (AT I. P. 171 sq.) и письмо Бекману (AT I. P. 157 sq.).

252

Этьен Жильсон уже отмечал эту типичную черту мышления Декарта: его куда меньше заботит установление факта, чем его объяснение. См.: Gilson E. Études sur le rôle de la pensée médiévale dans la formation du système cartésien. Paris, 1930.

253

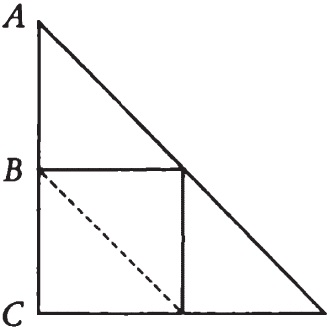
Descartes R. Cogitationes Privatae. AT X. P. 219: «Solvi quaestionem. In triangulo isoscelo rectangulo, ABC spatium [motum] repraesentat; inaequalitas spatii a puncto A ad basim BC, motus inaequalitatem. Igitur AD percurritur tempore, quod ADE repraesentat; DB vero tempore quod DEBC repraesentat: ubi est notandum minus spatium tardiorem motum repraesentare. Est autem AED tertia pars DEBC: ergo triplo tardius percurret AD quam DB. Aliter autem proponi potest haec quaestio, ita ut semper vis attractiva terrae aequalis sit illi quae primo momento fuit: nova producitur, priori remanente. Tunc quaestio solvetur in pyramide».

254

«Неравенство движения» – motus inequalitatem – т. е. изменение скорости.

255

Проблема разрешалась бы при помощи пирамиды – solvetur in pyramide – т. е. скорости возрастали бы в кубической, а не в квадратичной прогрессии.

256

Любопытно отметить, что у Бекмана, как и у Галилея (см. выше; Galile o G. Dialogo… // Le opere. Vol. VII. P. 251 (рус. пер.: Галилей Г. Избранные труды: В 2 т. Т. 1. М., 1964. C. 328); Discorsi…, Giornata III. Libro II. Prop. 1 и 2 // Le opere. Vol. VIII. P. 208–210 (рус. пер.: Галилей Г. Избранные труды: В 2 т. Т. 2. С. 248–250)), течение времени всегда представлено вертикальной линией, а не горизонтальной, как это привычно делать для нас. (Во-первых, у Койре содержится неточное указание на страницу итальянского издания Диалога – диаграмма движения падающего тела находится на с. 255; во‐вторых, в самом начале третьего дня «Бесед и математических доказательств», в трактате «О местном движении», теор. 1, Галилей изображает и пройденное расстояние, и время горизонтальными линиями. – Примеч. ред.)

257

Это решительное продвижение заключалось: а) в четком утверждении закона сохранения движения, которое таким образом освобождается от идеи импетуса; б) в устранении всякой внешней по отношению к движущемуся предмету причины. Впервые в истории естествознания изменчивый эффект может быть объяснен последовательным или длящимся действием постоянной силы.

258

Descartes R. et Beckman I. Physico-mathematica. AT X. P. 75 sq.: «In proposita quaestione, ubi imaginatur singulis temporibus novam addi vim qua corpus grave tendat deorsum, dico vim illam eodem pacto augeri, quo augentur lineae transversae de, fg, hi, et aliae infinitae transversae quae inter illas possunt imaginari. Quod ut demonstrem, assumam pro primo minimo vel puncto motus, quod causatur a primo quae imaginari potest attractiva vi terrae, quadratum aide. Pro secundo minimo motus, habebimus duplum, nempe dmgf: pergit enim ea vis quae erat in primo minimo, et alia nova accedit illi aequalis, Item in tertio minimo motus, erunt 3 vires; nempe primi, secundi et tertii minimi temporis, etc. Hic autem numerus est triangularis, ut alias forte fusius explicabo, et apparet hune figuram triangularem abc repraesentare. Immo, inquies, sunt partes protuberantes ale, emg, goi, etc. quae extra trianguli figuram exeunt. Ergo figura triangulari ilia progressio non debet explicari. Sed respondeo illas partes protuberantes oriri ex eo quod latitudinem dederimus minimis, quae indivisibilia debent imaginari et nullis partibus constantia. Quod ita demonstratur. Dividam illud minimum ad in duo aequalia in q; iamque arsq est [primum] minimum motus, et qted secundum minimum motus, in quo erunt duo minima virium. Eodem pacto dividamus df, fh, etc. Tunc habebimus partes protuberantes ars, ste, etc. Minores sunt parte protuberante ale, ut patet. Rursum, si pro minimo assumam minorem, ut aα, partes protubérantes erunt adhuc minores, ut αβγ, etc. Quod si denique pro illo minimo assumam verum minimum, nempe punctum, tum illae partes protuberantes nullae erunt, quia non possunt esse totum punctum, ut patet, sed tantum media pars minimi alde, atqui puncti media pars nulla est. Ex quibus patet, si imaginetur, verbi gratia lapis ex a ad b trahi a terra in vacuo per vim quae aequaliter ab ilia semper fluat, priori remanente, motum primum in a se habere ad ultimum qui est in b, ut punctum a se habet ad lineam bc. Mediam vero partem gb triplo celerius pertransiri a lapide, quam alia media pars ag, quia triplo majori vi a terra trahitur: spatium enim fgbc tripium est spatii afg, ut facile probatur. Et sic proportione dicendum de caeteris partibus».

259

Отметим по поводу «в каждый момент» – singulis temporibus; когда Декарт представляет «силу», он также представляет и «время».

260

Минимум движения или точка движения – minimun vel punctum motus – это совершенно то же самое, что Декарт называет «моментом» и что Декарт и его предшественники называли «степенью скорости».

261

П. Дюэм пишет на этот счет (Duhem P. Études sur Léonard de Vinci. Vol. III. P. 576): «Сказанное Бекманом [следовало бы, конечно же, сказать, «Декарт»] было более точно и ясно, нежели рассуждения механика из Пизы». Рассуждения «механика из Пизы» были не так плохи, как говорит Дюэм; они состояли, как мы видели и как мы еще увидим далее, в использовании геометрии неделимых Кавальери. Что касается декартовского рассуждения, мы находим очень похожие соображения у Гвидо Гранди (см.: Caverni R. Storia del metodo sperimentale in Italia. Vol. IV. Bologna, 1895. P. 306 sq.).

262

Эта теория совершенно верна, если только, как и Декарт, мы устраним время и представим, что сила действует вне времени или же мгновенно; тогда, как впоследствии скажет Ньютон (Newton I. Philosophiae naturalis principia mathematica. London, 1687. Axiomata sive leges. Lex II. P. 12; рус. пер.: Ньютон И. Математические начала натуральной философии. М., 1936. С. 40), нет сомнений в том, что «Si vis aliqua motum quamvis generit, dupla duplum, tripla triplum generabit, sive simul et semel, sive gradatuim et successive impressa fuerit». Про представление Декарта о мгновенном действии силы см. замечательный труд Жана Валя: Wahl J. Du rôle de l’idée de l’instant dans la philosophie de Descartes. Paris, 1920.

263

Мы уже говорили, что Бекман сам был далек от понимания того, что означал его «принцип». Это полностью подтверждают работы, опубликованные Корнелисом де Ваардом. Бекман считал, что он в каком-то смысле отрицает непрерывное ускорение при свободном падении и принимает теорию не непрерывного движения (см.: Correspondance de P. Mersenne. Vol. II. P. 291 sq.). Впрочем, он допускает, как и Аристотель, что тела, подброшенные в воздух, останавливаются перед тем, как упасть вниз. Сколь бы парадоксальным это ни могло показаться, очевидно, что для Бекмана это новое понятие движения отнюдь не ясно, и не кому иному, как Декарту, предстоит пролить на него свет и вывести из него все следствия. Но он придет к этому лишь десять, а то и пятнадцать лет спустя, в эпоху Regulae и Le Monde, когда решит рассматривать движение не иначе как математически.

264

Физика Декарта, увы, – это физика воображения, и довольно часто ясной идеей для него является не что иное, как идея, которую можно явно вообразить. См.: Brunschvicg L. Métaphysique et mathématique chez Descartes // Revue de métaphysique et de morale. 1927. Vol. 34. P. 277–324 и ниже, с. 177 и далее.

265

Ему нужно было лишь строго придерживаться параллели между силой и скоростью и продолжать мыслить в терминах причинности – т. е. учитывая время.

266

Descartes et Beeckman. Physico-mathematica. AT X. P. 77: «Aliter vero potest haec quaestio proponi difficilius, hoc pacto. Imaginetur lapis in puncto a manere, spatium inter a et b vacuum; iamque primum, verbi gratia, hodie hora nona Deus creet in b vim attractivam lapidis; et singulis postea momentis novam et novam vim creet, quae aequalis sit illi quam primo momento creavit; quae iuncta cum vi ante creata fortius lapidem trahat et fortius iterum, quia in vacuo quod semel motum est semper movetur; tandemque lapis, qui erat in a, perveniat ad b hora decima. Si petatur quanto tempore primant mediam partem spatii confecerit, nempe ag, et quanto reliquam: respondeo lapidem descendisse per lineam ag tempore ⅛ horae; per spatium gb, ⅞ horae (здесь, очевидно, ошибка: надо поменять местами цифры. – Примеч. Койре). Tunс enim debet fieri pyramis supra basim triangularem, cuius altitudo sit ab, quae quocunque pacto dividatur una cum tota pyramide per lineas transversas aeque distantes ab horizonte. Tanto celerius lapis inferiores partes lineae ab percurret, quanto majoribus insunt totius pyramidis sectionibus».

267

Линия (как и всегда для Декарта) представляет траекторию.

268

Т. е. пропорционально третьей силе. Это вторая гипотеза в «Cogitationes Privatae».

269

См.: Duhem P. Études sur Léonard de Vinci. Vol. III. P. 570.

270

См.: Milhaud G. Descartes savant. Paris, 1920. P. 28 sq.

271

Здесь в каком-то смысле повторяется ранее упомянутая история Леонардо да Винчи и Бенедетти.

272

См. письмо Мерсенну, 14 августа 1634 (AT I. P. 303; AM I. P. 265), где Декарт рассказывает, что полистал «Диалог…» Галилея, который одолжил ему Бекман с субботы до понедельника: «Господин Бекман пришел ко мне в субботу вечером и одолжил книгу Галилея; но он передал ее Дорту сегодня утром, так что она была у меня на руках каких-то 30 часов. Я не упустил возможности пролистать ее целиком, и я нахожу, что он весьма хорошо рассуждает о движении, хотя я нахожу полностью верными лишь очень немногие вещи, о которых он говорит; но что я успел заметить, это то, что он скорее ошибается там, где он следует уже полученным мнениям, нежели там, где он от них отдаляется. За исключением, однако, того, что он говорит о приливах и отливах, что я считаю немного притянутым за уши. Я также объясняю это в своем Le Monde движением Земли, но совершенно не так, как он.

Я хочу, впрочем, признаться, что встретил в его книге некоторые из моих собственных идей, в частности две идеи, о которых, мне думается, я писал вам однажды. Первая – это то, что пути, по которым проходят тяжелые тела, когда они падают, относятся друг к другу как квадраты времени, которое им потребовалось, чтобы опуститься, т. е. если мячу требуется три момента [времени], чтобы спуститься из точки А к точке В, то ему потребуется лишь один момент,

чтобы пройти далее от В до точки С и т. д. Вот что я говорил со множеством уточнений, поскольку в действительности это никогда не верно в полной мере, как кажется тому, кто доказывает». Ограничение Декарта любопытно, впрочем, оно вполне вписывается в его теорию; решение Галилея предполагает как существование пустоты, так и притяжение; с другой стороны, Декарт не признает ни того ни другого. Но здесь нас интересует не это, а тот факт, что Декарт считал, что нашел у Галилея свое собственное решение проблемы, которое на самом деле сильно отличается. Об этой разнице см. статью П. Таннери, которую мы цитировали выше.

273

Любопытно отметить, что П. Дюэм считал, что они одинаковы (см.: Duhem P. Op. cit. P. 569). Впрочем, чтобы понять рассуждения Декарта, Дюэм считал необходимым обратиться к рисунку, который их сопровождал (Ibid. P. 566).

274

Письмо Мерсенну, 13 ноября 1629 (AT I. P. 71; AM I. P. 85 sq.).

275

Отметим это уточнение: Бекман сказал лишь, что тело бесконечно и единообразно движется; Декарт уточняет, что оно движется с неизменной скоростью. Наверняка Бекман не подразумевал ничего иного, для него это само собой разумелось. Но это следовало уточнить, поскольку тело вполне может двигаться бесконечно, не оставляя свою скорость неизменной, и даже «единообразно двигаться», скажем, постоянно ускоряясь или, напротив, постоянно замедляясь. Закон сохранения движения, конечно, подразумевает сохранение скорости, но это необходимо объяснить. Декарту было достаточно прибавить к нему закон сохранения направления движения, чтобы сформулировать закон инерции. Это добавление достаточное, но также и совершенно необходимое. Также, вопреки мнению Дюэма (De l’accélération… P. 904) и де Ваарда (Correspondance du P. Mersenne. Vol. II. P. 236, 237), ни Декарт, ни Бекман ни в одном из процитированных нами текстов не формулируют принцип инерции.

276

Движение свободного падения в представлении Декарта оказывается быстрее, чем в действительности. На самом деле путь, пройденный за 3 и 4 «момента», равен 3² и 4², т. е. 9 и 16. Таким образом, неверно, что пройденное расстояние вдвое больше в течение четвертого «момента». Если бы Декарт помнил об этом расчете десять лет спустя, когда он читал «Диалог…», он не смог бы счесть, что его решение такое же, как у Галилея. Действительно, в то время как у Галилея пройденные расстояния в последовательные промежутки времени – sunt sicut numeri impares ab unitate, они не являются таковыми у Декарта. Но в то время, когда Декарт читал Галилея, он потерял всякую надежду на то, чтобы суметь дать точное числовое решение проблемы реального падения. И абстрактный случай падения в пустоте, рассмотренный Галилеем (и некогда самим Декартом), больше его не интересует: идея пустоты абсурдна, и для науки, построенной на ясных идеях, от нее не может быть никакого толка.

277

См. выше и далее.

278

Тяжесть последовательно порождает мгновенные силы, импетусы, которые заставляют тело двигаться и которые сохраняются в продолжение его движения. Здесь импетус, как и у Кардано и иногда у Галилея, отождествляется с движением и со скоростью – это пережиток старой идеи в новой науке. Что касается отхода от понятия притяжения, то это весьма типично для картезианского мышления; Декарт явно предпочитал этому неясному понятию (действие на расстоянии) понятие тяжести.

279

Разумеется, эти расстояния бесконечно малы.

280

В каком-то смысле это совершенно справедливо: ускорение действительно происходит в каждый момент движения.

281

Письмо Мерсенну, 18 декабря 1629 (AT I. P. 89; AM I. P. 97 sq.), в тексте на латыни.

282

В абсолютно пустом пространстве (лат.).

283

См.: «На заре классической науки» и далее.

284

Курсив Койре.

285

AT X. P. 349–488 (рус. пер.: Декарт Р. Правила для руководства ума // Соч.: В 2 т. Т. 1. С. 77–153).

286

См. знаменитые работы: Brunschvicg L. La сausalité physique et l’expérience humaine. Paris, 1925, и Brunschvicg L. Le Progrès de la conscience dans la philosophie occidentale. Paris, 1927.

287

См.: Bréhier E. Histoire de la philosophie. Vol. II. Paris, 1928. P. 93 sq.

288

См.: Meyerson E. Identité et Réalité. Paris, 1926. P. 282 sq. (рус. пер.: Мейерсон Э. Тождественность и действительность. СПб., 1912); Meyerson E. La déduction relativiste. Paris, 1925. P. 135 sq.

289

Письмо Мерcенну, 12 сентября 1638 (AT II. P. 355).

290

Письмо Мерcенну, 11 октября 1638 (AT II. P. 380): «В целом я нахожу, что он философствует гораздо лучше, чем толпа, – в том, что он оставляет как можно больше схоластических заблуждений и пытается изучать физические вопросы математическими средствами. В этом я полностью согласен с ним, и я считаю, что нет иного способа найти истину. Но я считаю, что он многое упускает, постоянно делая отступления и останавливаясь, чтобы истолковать предметы во всей полноте; это видно по тому, как он изучал их беспорядочно и, не рассмотрев первопричины природы, он лишь искал причины некоторых отдельных явлений, а также в том, что он строил без основания».

291

С определенной точки зрения Декарт справедливо критикует галилеевскую науку – если не фактически, то по крайней мере теоретически. По сути, Декарт упрекает Галилея за то, что тот создал математическую физику, которая противоречит здравому смыслу и повседневному опыту (см.: Le Monde // AT XI. P. 41; рус. пер.: Декарт Р. Соч.: В 2 т. Т. 1. С. 202), не имея на то права; т. е. не подкрепляя ее с помощью метафизики. Теоретически Декарт прав. Но фактически он ошибается: Галилей платоник.

292

Что есть тяжесть, легкость и длительность (лат.).

293

Письмо Мерcенну, октябрь–ноябрь 1631 (AT I. P. 228). В 1638 году (Письмо Мерcенну от 11 октября 1638, которое мы только что цитировали) Декарт писал (AT II. P. 386): «Он полагает, что скорость падающих тяжестей увеличивается всегда одинаково, так считал когда-то и я, подобно ему, но теперь, кажется, мне известно, благодаря доказательству, что это неверно», – лишь потому, что вывод Галилея основывается на понятии пустоты, и он пренебрегает (что невозможно) сопротивлением [среды] и движущей силой, обусловливающей ускорение. Наконец, в 1640 году Декарт писал (Письмо Мерcенну, 30 августа 1640, AT III. P. 164 sq.): «Я уже не раз писал вам, что отнюдь не допускаю, что скорость падающих тел всегда увеличивается in ratione duplicata temporum (в двойной пропорции ко времени (лат.)), однако я считаю, что скорость вполне может увеличиваться приблизительно таким образом, когда тело начинает падать, хотя это и не могло бы продолжаться дальше; и даже когда они достигают определенной скорости, они не могут далее ускоряться; и это подтверждается тем, что вы пишете про капли дождя и т. д.» Между тем отметим, что с тех пор, как он стал считать этот закон ложным, Декарт более не отстаивает своего авторства.

294

См.: Regulae ad directionem ingenii, XII (AT X. P. 419, 420) (рус. пер.: Декарт Р. Правила для руководства ума // Соч.: В 2 т. Т. 1. С. 123–125).

295

О движении (лат.).

296

Le Monde (AT XI. P. 39) (рус. пер.: Декарт Р. Соч.: В 2 т. Т. 1. С. 201).

297

Ibid. Р. 40 (рус. пер. с. 201).

298

Выделено авт.

299

Ibid. Р. 38 (рус. пер. с. 200).

300

Ibid. P. 38 (рус. пер. с. 200–201).

301

Следует отметить, что для Декарта и его последователей протяженность есть субстанция или сущностный атрибут, тогда как длительность они смешивают с бытием, так что время – это не что иное, как модус, причем субъективный.

302

Письмо Мерсенну, 16 октября 1639 (AT II. P. 593 sq.): «Чтобы понять, как тонкая материя, обращающаяся вокруг Земли, подгоняет тяжелые тела к центру [Земли], заполните несколько сосудов мелкими гранулами свинца и перемешайте со свинцом несколько кусочков дерева или другого вещества, более легкого, чем свинец, так чтобы эти кусочки были крупнее, чем гранулы свинца; затем, сильно взболтав этот сосуд, вы убедитесь в том, что те маленькие гранулы будут теснить все те кусочки дерева (или другой подобной материи) к центру сосуда, подобно тому как тонкая материя теснит земные тела и т. д.». О картезианской теории гравитации см. превосходное сочинение: Mouy P. Le développement de la physique cartésienne. Paris, 1934.

303

Письмо Мерсенну, 25 декабря 1639 (AT II. P. 635).

304

Письмо Мерсенну, октябрь–ноябрь 1631 (AT I. P. 230; AM I. P. 211).

305

См. ниже, III. На самом деле Декарт вовсе не отбрасывает понятие относительности, напротив, он его использует.

306

Почти в двойной пропорции (лат.).

307

Туаза – старинная французская мера длины, примерно соответствующая двум метрам. – Примеч. пер.

308

Письмо Мерсенну, 11 марта 1640 (AT III. P. 37 sq.). Ср. письмо Мерсенну, 11 июня 1640 (AT III. P. 79): «Причина, заставившая меня утверждать, что падающие тела менее теснимы тонкой материей в конце их движения, нежели в начале, не в чем ином, как в том, что [в конце движения тел] разница между их скоростью и скоростью этой тонкой материи меньше [чем в начале]. Так как, к примеру, если тело А, будучи неподвижным, сталкивается с телом В, которое движется к телу С с такой скоростью, что оно могло бы пройти один льё за четверть часа, [тогда тело А] будет двигаться, теснимое телом В – что не происходило бы, если бы оно уже само двигалось к телу С с такой скоростью, что могло бы пройти льё за полчаса, и оно и вовсе не будет теснимо им, если оно уже двигается настолько же быстро, как другое, т. е. так, что оно могло бы пройти льё за четверть часа».

309

Письмо Мерсенну, ноябрь–декабрь 1632 (AT I. P. 260; AM I. P. 234).

310

В природе вещей (лат.).

311

В пустоте (лат.).

312

В этом действительном воздухе (лат.). Ibid. (AT I. P. 231; AM I. P. 211). (Речь идет о другом письме, от октября или ноября 1631 года. – Примеч. ред.)

313

Галилей, как мы знаем, утверждал, что снаряд, брошенный горизонтально с высоты башни, коснется земли в тот же момент, что и другое тело, которое падало бы оттуда вертикально. См.: Galileo G. Dialogo sopra i due massimi sistemi del mondo tolemaico e copernicano // Le opere. Vol. VII. P. 181 (рус. пер.: Галилей Г. Диалог о двух главнейших системах мира – птолемеевой и коперниковой // Избранные труды: В 2 т. Т. 1. М., 1964. С. 254); и ниже: III, с. 188–189. Письмо Мерсенну, 19 августа 1634 (AT I. P. 305; AM I. P. 265. Ср.: P. 287).

314

Письмо Мерсенну, 22 июня 1637 (AT I. P. 392; AM I. P. 364). Ср. письмо Мерсенну, 12 сентября 1638 (AT II. P. 355): «Ибо невозможно сказать что-либо с толком и уверенностью в отношении скорости, не истолковав надлежащим образом, что есть тяжесть, а заодно и всю систему мира. Однако по причине, которую я не хотел бы развивать, я нашел средство опустить это соображение, отделив от него все прочие, так что я смог бы объяснить их без него. Ибо, хоть и не может существовать никакое движение, которое не обладало бы некоторой скоростью, все же мы можем рассматривать лишь возрастание и убывание этой скорости; говоря о движении предметов, мы полагаем, что оно осуществляется сообразно скорости, которая для него наиболее естественна, что то же самое, как если бы мы не учитывали ее вовсе».