Действуй, мозг! Квантовая модель разума

За это «сапиенсов» ждёт расплата: всякие новые технологии, о которых Харари рассуждает с недюжинной эрудицией на уровне самого осведомленного журналиста, преобразуют нас навсегда. В дурном, конечно, смысле.17

Составляя рецензию на эту работу, один научный критик проницательно назвал автора «восходящей рок-звездой лекционных выступлений» и отметил, что тот обладает «смутным мировоззрением, обремененным политкорректностью». 28

Дальше – больше.

Новым технологиям и, прежде всего, «всемогущим компьютерным алгоритмам» Юваль Харари всыпал по полной в следующей книге – «Ноmo Deus. Краткая история будущего».

Мыслитель решил, что «наука давно доказала» тождество «биохимических алгоритмов» и алгоритмов компьютерных программ. «Сейчас считается истиной в последней инстанции, что организмы – это алгоритмы, а алгоритмы могут быть представлены математическими формулами». А так как компьютеры развиваются быстрее, чем человеческий мозг, нам всем будет худо.

Заметно, что Харари тщательно нагнетает технофобию и наслаждается этим: «нейронные сети будут заменены умным „софтом“, не скованным органической химией и способным свободно ориентироваться как в виртуальном, так и в невиртуальном пространстве»; «алгоритм сможет предсказывать ваши мнения и желания лучше, чем ваши муж или жена!».

Очень забавно читать про то, как Харари, претендующий на роль исследователя-пионера, объясняет мозг. Автор «Ноmo Deus» выделяет в психике «переживающее „я“» и «комментирующее „я“». Первое – нечто рациональное (отражает объективные потребности), второе – иррациональное (выдумывает всякую субъективную ерунду). При этом Харари ссылается на нейробиолога Роджера Сперри, чьи работы 1970х гг. по изучению межполушарной асимметрии головного мозга трактует, как интернет-психолог, раскручивающий свой ютуб-канал: «правое полушарие отвечает за творчество, левое – за логику».

Книга насыщена дихотомиями и их оппозициями: наука против религии, механическое против живого, разум против чувства, интеллект против сознания. Последнее понятие – ключевое. Правда, по давней привычке пустословов и компиляторов, Юваль Харари забывает объяснить, что же это такое, таинственное «сознание». По скупым характеристикам можно лишь гадать: это нечто, позволяющее нам «заботиться, грезить, сомневаться».

Ближе к финалу произведения ожидаемо является теория заговора. Оказывается, злонамеренные «техногуманисты» мечтают совершить «вторую когнитивную революцию». В результате которой мы превратимся «в людей-винтиков» или станем «сильно увеличенными муравьями». А править нами будет, конечно, он – искусственный интеллект.16

В последней книге профессор окончательно разбушевался.

Стиль бомбардировки эмоциональными аргументами и сообщения скороговоркой устаревших (а порою – откровенно недостоверных) фактов вышел на новый уровень.

Тут вам: тоска и боль за будущее человечества; сенсационный «факт» о том, что учёные «взломали» мозг и расшифровали «хвалёную человеческую интуицию»; тревога из-за того, что компьютеры способны быстро объединяться в сети, вперемежку с «фактами» о том, как они уже диагнозы ставят и назначают лечение.

«Основное блюдо» всё то же: сопротивляйтесь! сражайтесь, а не то будет поздно! я вас предупредил!

В этом опусе учёный-гуманитарий, наконец-то, делится своим представлением о мозге: «…интеллект и сознание – совершенно разные вещи. Интеллект – это способность решать задачи. Сознание – способность чувствовать боль, радость, любовь или гнев. Мы часто путаем эти понятия, потому что у людей и других млекопитающих интеллект неразрывно связан с сознанием. Млекопитающие решают большинство задач посредством чувств. Но у компьютеров совсем другой подход». 18

Ах, ты ж, боже мой. А ведь автор про нехорошую и манипуляторскую «постправду» сочиняет…

«Говорящие головы» бесконечно далеки от проблем реальной жизни. Свои книги они пишут не для того, чтобы объяснять или – упаси бог! – просвещать. А для банального хайпа. Рецепт незамысловат: побольше апломба, полярных эмоций и утверждений с широко раскрытыми глазами. Знание тут – лишний ингредиент.

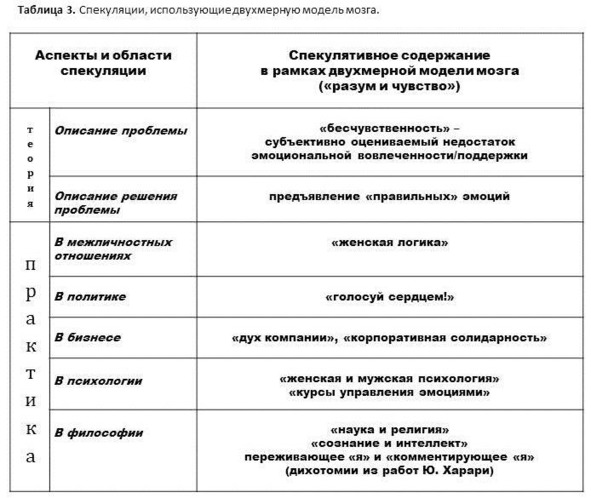
Так готовятся все современные спекуляции на двухмерном мозга. Человек, верящий в то, что его мозг сводится к «разумному» и «чувственному», уже подготовлен к суррогату. Лишь бы было покороче и позабористее (см. табл. 3).

Отдаю полный отчёт в том, что фанатов двойственной природы человека переубедить не удастся.

Большинство мелодраматических сюжетов ещё долго будут строиться вокруг гадания на ромашке «любит/не любит». А нынешним воротилам мысли и спекулянтам, глубокомысленно противопоставляющим «интеллект» и «сознание», не грозит ничего, кроме безбедного существования.

Однако преданность идее двухмерного разума, которую демонстрирует ставшая глобальной, интеллектуальная элита, изумляет.

Да, мы живём на стыке эпох. Да, все озабочены утратой старых смыслов.

Как-то вдруг всё перестало работать. Или работает натужно, со сбоями: демократия, религия, просвещение.

И даже, как грезится многим, сама мать-природа восстала против нас, грешников-потребителей, грозя неминуемой экологической и/или биологической катастрофой.

Но являются ли трудности переосмысления достаточным поводом, чтобы погрузиться в уныние, махнуть рукой? И, кряхтя под свалившимся на каждого из нас информационным грузом, рукоплескать обманчивой простоте «женской логики»? Которая не только пользует дихотомию «разумное/чувственное», но и сама есть её побочное, нелюбимое, дитя?

Как бы это ни величали – психофизиологическая проблема, основной вопрос философии или как-то ещё – ничего путного не выходит. Старая модель выдохлась, и никакие косметические ухищрения её уже не спасут.

От того, что сегодня мысли называются «когнициями», а чувства и эмоции камуфлируются в полумистическое понятие «квалиа», суть дела не меняется.

Как и две с половиной тысячи лет назад, мы ставим себя в рамки ложной оппозиции. Гадаем: тело или душа, разум или чувство, курица или яйцо.

Не надо считать дураками наших предков. Сочинивших очень сложную и красивую сказку, вдохновлявшую на творчество и любовь.

Но не надо считать дураками и самих себя. Не способными выдумать ничего лучше.

Чувствующий мозг – наше изощренное психологическое наследие. Не найдётся ли чего посовременнее?

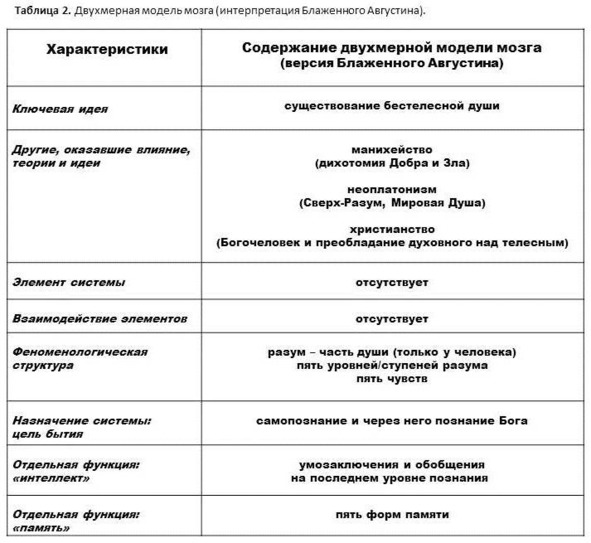
Таблицы к главе 2

Глава 3. Мозг-машина

Наши ноги —

поездов молниеносные проходы.

Наши руки —

пыль сдувающие веера полян.

Наши плавники – пароходы.

Наши крылья – аэроплан.

поэт Маяковский безбожно врёт

Я не нуждался в этой гипотезе

математик Лаплас, отвечая на вопрос о Боге, троллит общественность

Третье измерение

В конце XVII века сэр Исаак Ньютон своим фундаментальным трудом «Математические начала натуральной философии» заложил основы т.н. «естественнонаучной» картины мира.

Считается, что физик заочно полемизировал с другим выдающимся учёным, математиком Рене Декартом. Который в 1644 году опубликовал не менее крупную по своему онтологическому значению работу «Первоначала философии», где представил деистический взгляд на природу.

Декарт полагал, что духовное и телесное сосуществуют, и первое, безусловно, влиятельнее второго. Ньютон механически, с помощью дифференциальных уравнений, описал окружающий мир. Он невольно поместил Бога-Творца «за скобки», лишив его функции текущего ремонта.

При этом Ньютон критиковал гипотезу Декарта, согласно которой планеты движутся благодаря полумифическим эфирным вихрям, и с подозрением относился ко всяким попыткам отвлечённого философствования.16

Тем не менее, учёные сходились в главном. Вселенная есть большая и слаженно работающая машина. Если так, то и сам человек, и его разум подобны машине.

Ньютон на этом следствии останавливаться не стал: возможно, оно казалось ему чересчур мелким в сравнении с задачей моделирования мироздания. А, вот, Декарт прямо применил образ машины для объяснения мозга.

«Первоначала философии» начинаются с того, что автор повторяет формулу Блаженного Августина: человек = тело + душа. Про последнюю уточнялось: «…есть то, что мы именуем нашей душой или способностью мыслить».

Далее, развивая тезис, Декарт замечает, что «различие между душой и телом, или между вещью мыслящей и телесной» есть «наилучший путь к познанию природы ума и его отличия от тела».

И, наконец: «Под словом „мышление“ я понимаю всё то, что совершается в нас осознанно, поскольку мы это понимаем. Таким образом, не только понимать, хотеть, воображать, но также и чувствовать есть то же самое, что мыслить». 10

По Декарту, способность мыслить является неоспоримым доказательством существования Бога: его бесконечной мудрости и всемогущества.

Ведь, как рассуждал учёный, если сомневаешься, то совершенный затем через преодоление сомнения выбор, по определению, свободный. Не исключая выбор метафизический (воплощенный, например, в вопросе: есть ли Бог?).

А «свободный» (или, если угодно, «произвольный») значит «истинный». Не в том смысле, что соответствует истинному («объективному», как сказали бы сейчас) положению вещей, а в значении «искренний».

Выбор может быть ошибочным, но его ценность для познания от этого не становится меньше. Наоборот, способность заблуждаться делает человека человеком – лучшим и любимейшим творением Бога.

Из Августинова «Если ошибаюсь, я существую» (лат. Si fallor, sum) часто выводится Декартов принцип радикального сомнения, выраженный в его знаменитом «Я мыслю, значит, я существую» (фр. Je pense, donc je suis).

Создаётся обманчивое впечатление, что математик пошёл по стопам теолога. В предыдущей главе мы выяснили, что Блаженный Августин создал проработанную концепцию о двухмерном мозге. Рене Декарт, как будто, описывал ту же конструкцию. Некоторые нейроучёные до сих пор поддерживают точку зрения о том, что Декарт проповедовал дуализм: искусственно разделял рациональное и чувственное.31

Не берусь судить, насколько Декарт был дуалистом в отношении прочих явлений природы, но наш разум в прокрустово ложе антиномий он уж точно не помещал.

Подмеченное Августином свойство мозга сомневаться – в том числе, в бытии Бога – Декарт использовал, как представляется, для других целей.

У Отца Церкви это иллюстрация безграничной силы и доброты Творца по отношению к человеку. У математика – отражение особой, чисто человеческой, структуры: иного, не телесного и не душевного, измерения.

В трактовке Декарта третье измерение нашего мозга – способность взглянуть на себя (на свои мысли, чувства, идеи, поступки и т.д.) со стороны. То, что сейчас иногда зовётся самосознанием/саморефлексией.

Вне всяких сомнений, это новое слово в описании мозга.

Ещё раньше, до публикации «Первоначал философии», Декарт, отвечая на разнообразную критику, приводил следующий мысленный эксперимент.

Вообразите, что возле камина сидит человек. Он ощущает жар огня и думает о нём.

Огонь есть проявление материи. А мысль о наблюдаемом огне или ощущение жара (по Декарту, между ними нет существенной разницы) – проявление работы мыслящей души (или одухотворенного разума).

Однако есть кое-что ещё. А именно: обдумывание видения огня и обдумывание ощущения жара. В частности, имеет место быть размышление о природе связи между ощущением от действия огня и тем, что разум обозначает как «жар». Это мысль о мысли.12

Возникает резонный вопрос: чем «мысль о мысли» отличается от просто «мысли»? Не является ли это избыточным теоретическим усложнением?

Нет, не является.

В «Первоначалах философии» Декарт поясняет, что, по крайней мере, для человеческого мозга первичное восприятие следует отличать от вторичной обработки информации. «Нам присущи два модуса мышления – восприятие разума (perceptio intellectus) и действие воли (operatio voluntatis). Разумеется, все имеющиеся у нас модусы мышления сводятся к двум основным: один из них – восприятие, или действие разума, другой – воление, или действие воли».

Таким образом, ощущение жара и даже присвоение ему названия есть обычная перцепция, которой обладают животные. А, вот, соединение материального раздражителя и его восприятия, т.е. отношение этих величин, в форме абстрактного размышления – исключительно человеческое.

Причём оно основано на свободе выбора. Мы вольны размышлять о природе огня-жара так и этак, а можем вообще этого не делать, просто наслаждаясь теплом пылающих поленьев.

Именно воление, по Декарту, является причиной заблуждений. Оно же – источник верных догадок и конструктивных идей.

В связи с этим математик приводит замечательное рассуждение: «Что же до воли, то область её действия чрезвычайно обширна (что, несомненно, согласуется с её природой), и высшим совершенством человека является свобода волений; таким образом, он в некотором особом смысле хозяин своих поступков и сообразно с ними заслуживает хвалы. Ведь автоматы нельзя хвалить за то, что они аккуратно выполняют все движения, к которым предназначены, ибо они выполняют их так в силу необходимости; однако хвалят создавшего их мастера за то, что он сработал их с такой точностью, ибо он создал их не в силу необходимости, а по произволу». 10

Сегодня такое рассуждение не кажется оригинальным.

Говорят: «человеку свойственно ошибаться», а современный поэт выразил эту мысль ещё лучше: «Сомненье – лучший антисептик / От загнивания ума». 8

Однако сказать подобное в XVII веке – сенсация.

До Декарта двуединая природа человека была продуктом тщательной логической проработки (начало которой положил тот же Августин). Бессмертная душа и смертное тело – не просто красивые метафоры, но ещё системы целеполагания. Душа стремится к Богу, тело предрасположено к греху. На этом противопоставлении строится важнейшая христианская концепция «первородного греха». Причину которого, например, Фома Аквинский связывал с присущей человеку волей.25

Следовательно, доминировало убеждение, что всё истинное, непротиворечивое, ясное и простое – от души, а всё ошибочное, сомнительное, смутное, избыточно сложное – от тела.

И, вот, вся схема рушится. Или, во всяком случае, ставится под сомнение.

Возможно возражение со стороны тех, кто продолжает считать Декарта дуалистом: мол, ничего нового в разделении мозга на три части не было.

Вспомнить хотя бы Галена с его концепцией о трёх одухотворённых пневмах. Или, вот, Бонавентура, горячий поклонник трудов Блаженного Августина: он полагал человека триединым существом, наделённым ощущающей частью, душой и умом.15

Однако эти возражения несостоятельны.

У Галена разного рода пневмы, хоть и помещены в различные органы, ничем принципиально друг от друга не отличаются. А что касается Бонавентуры, в его интерпретации речь и вправду идёт о частях. Переплетенных и, при некоторых оговорках, взаимозаменяемых.

Декарт же описывал «действие воли» как самодостаточную категорию мозга. Третье, саморефлексирующее, измерение.

Которое не сводится ни к автоматическим движениям тела (когда мы, например, касаясь огня, одёргиваем руку), ни к мыслям-чувствам (идентифицируем «огонь-жар», глядя на него и/или ощущая его непосредственно).

Новизна Декартова рассуждения в том, что созерцание собственного мышления есть нечто независимое в человеческом мозге. У него свои законы, свои правила. И, между прочим, собственный локус. Орган, где телесно-механическое и душевно-мыслящее сходятся – шишковидная железа (эпифиз).11,37

Это то, что отличает нас от прочих живых существ. Ибо жить без самосознания можно, но, сознавая себя, нельзя не быть человеком. Поэтому: «Я мыслю, значит, я [как человек – Р.Б.] существую».

Как Декарт сумел додуматься до третьего измерения мозга? Почему он, а не, скажем, Андреас Везалий – блестящий врач, живший на сто лет раньше и своими анатомическими исследованиями во многом исправивший ошибки Галена?

Догадка Рене Декарта – не чудо и не случайность. Это закономерный результат его профессиональной деятельности. До конца жизни он оставался превосходным математиком.

Мнимые числа

Прежде чем совершить прорыв в теории мозга, Декарт совершил революцию в математике. Суть переворота заключалась в переосмыслении понятия «число».

По мнению сэра Майкла Атья, в истории математики такие учёные, как Ньютон и Лейбниц, знаменуют переход от алгебры к математическому анализу.29

Не углубляясь в предпосылки данного перехода, заметим, что существенной его чертой было появление дифференциального исчисления и термина «функция».

Думаю, сейчас все знают, что функция есть отношение двух величин (необязательно выраженных числом – существуют, например, векторные функции). Однако, чтобы прийти к современному пониманию числа и функции, человечество преодолело немалый путь.

Со школы каждому знакома двухмерная система координат (ось абсцисс – x и ось ординат – y с их числовой разметкой), в которой исследуются различные функции (всякие эллипсы, параболы, гиперболы и пр.).

Мало кто задумывался (я в школьные годы – точно нет), что графическое изображение функции есть удивительный пример человеческой фантазии, соединившей, казалось бы, мало сопоставимые вещи: геометрию и алгебру.

В данном случае фантазия принадлежала Рене Декарту. Его трактат «Геометрия», увидевший свет в 1637 году (за семь лет до «Первоначал философии»), продемонстрировал новый универсальный подход к решению математических задач.

А именно: любые объекты и их соотношения можно выразить через алгебраические уравнения. Декарт строил двухмерную систему координат (теперь говорят «декартовы координаты»), изображал два пересекающихся объекта (например, окружность и параболу), выражал каждый объект через уравнение, объединял получившиеся уравнения в систему и решал её. Полученные корни являлись координатами (по оси абсцисс) точек пересечения объектов.9

Для того чтобы понять, как Декарт от математики шагнул к оригинальной идее об устройстве мозга, предпримем попытку воспроизвести его логику.

В целях упрощения изложения рассмотрим в плоскости декартовых координат объекты: параболу (x2 = y) и несколько, пересекающих её, прямых (y = ¼; y = 1; y = 2; y = 3; y = 4).

Указанные объекты пересекаются в некоторых точках (геометрическая характеристика), имеющих соответствующие координаты и, в частности, определенные числовые значения на оси абсцисс (алгебраическая характеристика).

Среди этих значений есть, как отрицательные, так и положительные, числа: целые (—2; —1; 1; 2), в виде обыкновенной дроби (—½; ½) и т.н. «иррациональные» (—√3; —√2;√2;√3) (см. рис. 7).

Иррациональные числа были известны задолго до Декарта (скажем, число π).

Надо сказать, что большинству математиков они не нравились (при попытке их уточнения – попробуйте, например, извлечь квадратный корень из 2 или из 3 – выползает «некрасивая» десятичная дробь с длинным-предлинным бесконечным хвостом). Некоторые даже не считали их числами.

Рене Декарт покончил с этой своеобразной дискриминацией, расширив теоретическое представление о числе. В «Геометрии» он фактически объявил то, что спустя несколько десятилетий сформулировал Ньютон: число – отношение одной величины к другой.

В результате этого отношения могут получаться целые, дробные, иррациональные и даже отрицательные значения.

Важно не это, а то, что за каждым числом стоит некий смысл (скажем, π является постоянным значением отношения длины окружности к её диаметру; или, например, в медицине бессмысленно подсчитывать количество больных на данной территории, но полезно выяснить отношение больные/здоровые, больные/всё население и т.д.).

Только за одно это толкование понятия «число» мы, благодарные потомки, наставили бы Рене Декарту памятников. Но математику этого было мало: он стал рассуждать дальше.

Декарт задумался: насколько вообще допустимо совмещать геометрию и алгебру – это и вправду важно на практике или просто отвлечённая игра ума? получающиеся в координатной сетке точки пересечения объектов, как и сами объекты, реальны? или они, поскольку заданы абстрактными комбинациями цифр, суть умозрительные конструкции, часть из которых хоть и имеют какой-то смысл, но большинство, как почти все иррациональные числа, бесконечно непостижимы?

Поясним суть проблемы на нашем примере.

Возьмём параболу, заданную функцией x2 = y, и пересекающуюся с ней прямую, заданную функцией y = 1. По методу Декарта, составим систему уравнений и найдём корни: x1 = —1, x2 = 1. Получим координаты двух точек пересечения для данных объектов: (—1; 1), (1; 1).

Аналогичные операции проделаем для каждой другой пары параболы и прямой – получим соответствующие значения координат.

Заметим, что значения всех функций в точках пересечения объектов будут всегда положительными. Т.е. y – строго положительное число.

Обобщая, можно сказать, что совокупность уравнений, отражающих функции, есть правила, по которым строятся реальные (в том смысле, что допустимо создать их в физической реальности: в самом простом случае – нарисовать на бумаге) геометрические объекты. А совокупность числовых координат локусов пересечения объектов есть точки – тоже реальные (их можно вычислить по правилу) корни уравнений (см. рис. 8).

Пока вроде бы ничего сложного: всё яснее ясного.

Но Декарт решил усложнить себе жизнь и перевернуть параболу «вверх ногами» – рассмотреть зеркальное отображение объекта, заданного функцией x2 = y.

Или, иначе говоря, математик исследовал, в контексте приведённого выше обобщения, функцию x2 = ƒ, где ƒ – это строго отрицательное число.

Вероятно, идея пришла к нему из оптики, которой учёный активно занимался. А, может, его осенило, когда он смотрелся в зеркало: ведь «мнимое изображение», несмотря на всю условность своего существования, чем-то да является.

Как бы там ни было, перевёрнутая «вверх ногами» парабола – очень странный объект. Реальна ли описывающая его функция?

По методу Декарта, составим системы уравнений для параболы, заданной функцией x2 = ƒ, и двух пересекающихся с ней прямых, например, y = —1 и y = —3. Попытаемся найти корни.

Не выходит. Потому что получаются уравнения: x2 = —1; x2 = —3. И, значит, x = √—1; x = √—3.

Квадратный корень из отрицательного числа – это что?

Это мнимые числа.

Такие числа ранее математики уже вычисляли, решая некоторые сложные уравнения. Им не придавали особого значения, поскольку наряду с подобными, казавшимися абсурдными, результатами получались и «нормальные» корни.

Декарт тоже их игнорировал, однако, во-первых, взявшись написать о числах всё, что знал, включил их в общую классификацию (термин «мнимые числа» принадлежит ему), а, во-вторых, в его программе создания общего метода решения математических задач их надо было как-то объяснить.

Ведь, несмотря на алгебраическое затруднение, геометрические объекты x2 = ƒ, y = —1, y = —3 существуют. В системе координат их можно построить и легко найти координаты точек пересечения. По две точки для каждой пары соответственно: (—1; —1) и (1; —1); (—√3; —3) и (√3; —3).

Значит, геометрические объекты реальны.

Но, поскольку функция-правило, согласно которой строится один из объектов, скажем так, не совсем реальна (функция типа x2 = — y), координаты общих для этих объектов чисел-точек содержат «мнимые числа».

Т.е. данные точки нереальны (см. рис. 9).

Полагаю, будучи подлинным учёным, Декарт таким результатом нисколько не смутился. Что получилось, то получилось.

Свойство «мнимости» не помешало распространить логику соотношения величин и на эти, несподручные, числа.