The Book of Wonders

Back in seething Alexandria, where the building work is still going on and the streets are ever more crowded. By the end of Euclid’s life the great lighthouse at Pharos has been built (did the architects consult Euclid? It would be intriguing to think so); the library and Museum are nearing completion and the palace complex is grander than ever. The Elements is finished: thirteen rolls of papyrus covered with neat columns of text and diagrams. And Euclid is still teaching, still taking on new students.

One beginner is impatient, like the king before him. After he has understood the first proposition he bursts out, ‘What is my profit now that I have learned that?’

A glance of contempt, or perhaps of pity. Euclid calls for a servant. ‘Give him threepence, since he must always make a profit out of what he learns.’

Another romantic legend, perhaps: one that circulated later in Greece, during its period of Roman domination. Like the ‘royal road’ story, it helped to protect Euclid from the whiff of servility, of sycophancy that hung over anyone connected with Ptolemaic Alexandria and its institutions. It preserved and dramatised the idea that geometry was a leisured, cultured pursuit, part of the life of the mind. Not a profitable trade, but pure, truthful and beautiful for its own perfect sake.

Some 350 geometrical propositions in the driest of styles. It’s an odd thing, to have become one of the most enduring cultural artefacts of the Greek world. Ptolemaic Alexandria is largely dust today; a few wrecked statues are dug from the ground or pulled from the sea from time to time, but the splendour is all gone. Ptolemy’s dynasty died with Cleopatra. The library is scattered. But the books – the Elements among them – the books lived.

Elephantine

Pot shards

Elephantine island, Upper Egypt, in the reign of Ptolemy III (r.246–221 BC; grandson of Ptolemy I). A Greek garrison at the end of the world. One man, off duty, is writing.

He grabs the nearest thing to hand to write on: a few broken pieces of pot. Scratch, scribble. A quick diagram, a few lines of text. His hands are confident; only slightly less confident is his memory of the mathematics. Is this how it worked? Or this? Ah, that’s right.

And, his mind and hand refreshed, the potsherds, the cheapest available writing material – perhaps the cheapest possible – go into the rubbish heap where they belong.

Euclid’s original manuscripts do not survive, nor anything like them. The papyrus on which he wrote is durable enough, in the right conditions. Scrolls hundreds of years old were not terribly unusual in the ancient world, and they could remain smooth, pliable and legible for much longer. A story is told of a museum curator who used to display the strength and flexibility of papyrus by blithely rolling and unrolling an Egyptian sheet 3,000 years old (this was in the 1930s, when attitudes to museum artefacts were perhaps less reverent than today).

In the right conditions, that is. Most conditions are not right. If it gets too wet, papyrus rots; too dry and it crumbles. Insect larvae like papyrus, and the worms destroyed many a literary reputation in the ancient world. So did the rats. Plus, the long rolls tore easily and were thrown away when they did. The upshot is that large or complete papyri surviving from the ancient world are extremely rare. What more often survive are fragments: discarded rolls, pieces reused to make mummy cases, pieces recovered from rubbish dumps or ruined houses. Rough, dark and brittle with age, nearly all are from provincial locations in Middle and Upper Egypt, where the dry conditions preserved them. Finds have come from cemeteries along the Nile Valley and in the Faiyum Oasis, and from certain villages. From the big towns, by contrast, there is next to nothing: Alexandria itself, having a high water table, has no preserved papyri at all.

For all that, there are a lot of papyrus fragments. People have been systematically digging them out of the ground since the mid-nineteenth century, and hundreds of thousands are now amassed. And, yes, some of them contain fragments of Euclid’s Elements. Seven, in fact, totalling about sixty complete lines of the text and another sixty fragmentary lines.

What parts of the Elements do they preserve? They include, written around 100 BC: three propositions from book 1, with one summary proof (these come as citations in a philosophical treatise preserved – carbonised – in Herculaneum by the eruption of Vesuvius in AD 79: an exception to the normal generalisations about papyrus survival). An enunciation from book 2, with a rough figure, written in the Egyptian city of Oxyrhynchus around AD 100. Parts of two more propositions from book 1, written at Arsinoë (modern Faiyum) in the second half of the second century AD. A second-century copy of three figures and enunciations from book 1, carefully written with ruled diagrams. And a schoolteacher’s or pupil’s copy of the ten opening definitions, made in the third century AD.

It is not much: these are small pieces from the easy parts of the book, in one case from its very beginning. But they do reveal something about the way the Elements was spreading. It did not just stay in Alexandria: already, by the first few centuries after its composition, it – or parts of it – was being copied out by people hundreds of miles away around the Greek-speaking world. It was moving out from the cultural centre to the provinces.

Euclid’s Elements will have been published in the ancient sense: sent to a scribal copying house which produced multiple copies for sale. But most of the papyrus fragments are not from those copies; only the Faiyum fragment looks like the work of a professional scribe. Instead, they bear witness to the activity of individuals copying out parts of the text for their own use, teaching or learning.

So, the writers of these papyrus fragments represent the ‘public’ for Greek geometry: a tiny minority, in a world in which the literate themselves were already a minority. These were people who understood geometry, who accepted and shared its conventions, who knew enough of the basics and the methods to comprehend Euclid’s book. Their needs surely shaped what was written and how it was written. The very packaging of mathematics in a self-contained written form already presumes that they existed. But nothing more is known about them.

And this evidence can tell only about those places where it was dry enough to preserve papyrus fragments: for the rest of the Greek world – the islands and the mainland north of the Mediterranean, for instance – the lack of evidence reveals nothing, positive or negative. Surely the Elements went to Athens, for example: but it is centuries before there is evidence for that.

As well as papyrus there was a cheaper writing surface still: ostraka or pot shards. Literally, broken pieces of pot: waste, and therefore free. Ostraka were used in Egypt before the Ptolemies and up to the end of antiquity, in Athens from the seventh century BC: they were written on in ink or simply scratched, to form pictures or writing in Hieratic, Demotic, Greek, Coptic or Arabic as the case might be. Schoolboys, soldiers, priests and tax collectors all used them. (They were also used as voting tokens: if the word sounds familiar it is because ‘ostracism’ was a procedure for expelling a man from the country for ten years on suspicion of disloyalty: the votes were written on ostraka. It happened at Athens for most of the fifth century BC, and in other Greek cities too.)

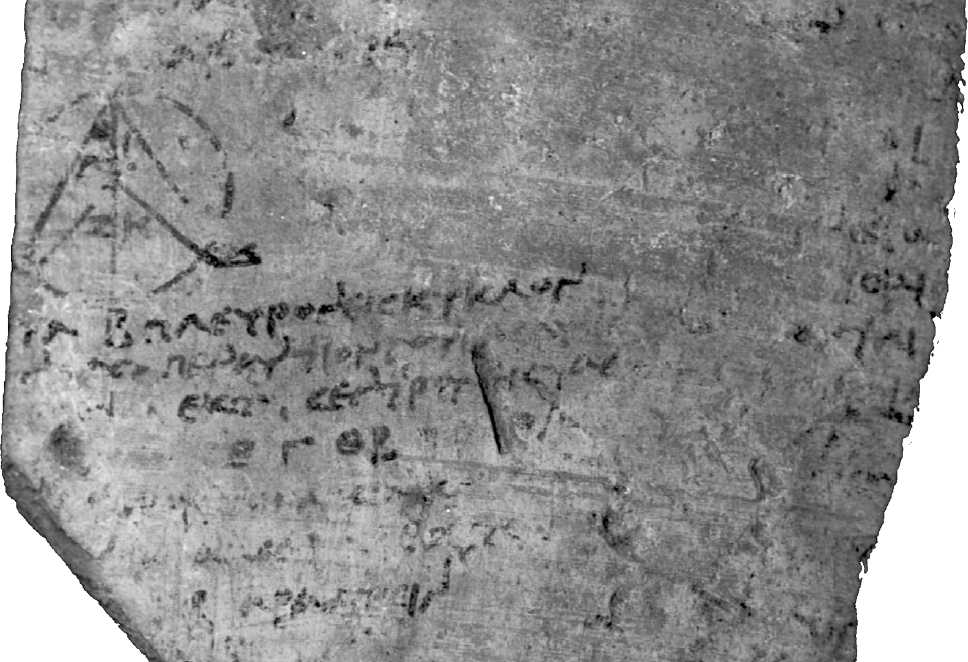
A Euclidean ostrakon.

Ostrakon, Elephantine, third century BC. Berliner Papyrusdatenbank P. 11999. (© bpk-Bildagentur)

A set of ostraka bearing geometrical writing, written at Elephantine, were preserved by the random sieve of history. They were dug up by German archaeologist Otto Rubensohn in the winters of 1906 and 1907, and they are now held with the papyrus collection at Berlin; their contents were transcribed and published in the 1930s. They are the oldest surviving physical evidence for any part of Euclid’s Elements.

Elephantine is more than 500 miles south of Alexandria: an island in the Nile at the northern end of the first cataract. In the third quarter of the third century BC, when the ostraka were written, it was the frontier of the Ptolemaic kingdom. Traditionally the ‘ivory island’ or ‘elephant island’, whose settlement stretched back into prehistory, it was the capital of the first Upper Egyptian administrative district or ‘nome’, controlling trade with the quarries of the cataract region and the trade route to Nubia. It was a garrison town, far removed from the centres of Greek culture, under threat from brigands.

It had temples, priests, fairly elaborate housing and a degree of bustle; by the Byzantine period the town had a public camel yard. But the documents that have survived – papyri again, mainly – are dominated by the characteristic anxieties of soldiers settled far from their widely diverse homelands. In the third century BC there were men at Elephantine from Greek cities and islands as far afield as Crete and Rhodes as well as Alexandria and the mainland at Euboea and Phocis: a veritable Homeric catalogue of soldiers. They kept aloof from the native Egyptians, referring to their town as ‘the fortress’, and the papyri show them making wills, marrying, appointing guardians, providing accounts to their superiors or petitioning them for justice. It seems a most unlikely setting for the earliest Euclidean evidence.

The ostraka – six of them, one clearly broken on all sides – bear a text concerned with constructing a regular polyhedron. It relates to propositions 10 and 16 in book 13 of the Elements: that is, from very near the end of the book. In those propositions a pentagon, hexagon and decagon are employed to build up an icosahedron: a regular solid with twenty sides, all of them equilateral triangles. The inevitable diagram is clearly present on one of the ostraka, with its letter labels, and the shards give a clear sense of someone doing what every Greek geometer did: draw a picture and tell a story about it.

The propositions in the Elements depend on one another in an elaborate, tree-like structure, each one referring implicitly to many that have come before. To be confident in something from this late in the book, a person would need to have studied much of what came before it: but the ostraka provide no direct evidence for that. The text is in a confident, flowing handwriting, too: that of an experienced writer whose grammar and spelling were unhesitating and correct.

Who was the writer? It is most frustrating not to know. Serafina Cuomo, historian of ancient mathematics, remarks of these ostraka that ‘while their contents denote a high level of education, both the humble material and the location (a remote outpost in the heart of “Egyptian” Egypt) seem to jar with that conclusion’. Priest, teacher, soldier or camp follower? It will never be known whose were the hands that scratched out this earliest surviving piece of Euclideana.

There is a further twist. The matter discussed on the ostraka came straight from Elements book 13, but their text is not the text that has been transmitted as part of the book. It is the same diagram, and the same ideas, but the words are not exactly the same. That is also true, albeit to a lesser degree, of the other early fragments that survive from the Elements, on papyrus: their versions of the text do not exactly match what has been preserved in later, more complete versions of the book.

This reinforces the sense that Greek geometry was essentially a performance, consisting of drawing a diagram and talking about it, to oneself or to an audience. What was written down was a transcript of the performance, an aide-memoire, a skeleton or a set of prompts, together with the finished, static version of a diagram that, in use, had been dynamic and growing. Those written traces could be of use for private study or a help for a teacher, who would need to perform the same proof several times. They could also, as in a book like the Elements, transmit the idea of the proof or construction to people far away in time or place.

And, as a result, reading a geometric proof is not like reading a novel or a poem. You can only really follow it by recreating the original live performance; by picking up a pen and some scrap paper, papyrus, or a shard of pot, and constructing the diagram as you read, so as to see how it grows.

So the written forms of Greek geometric propositions were not so much something one would learn and copy slavishly as prompts that said: here is something interesting; try it yourself. The Elements was not a dead repository of facts but a support for learning and practice; an invitation to perform for oneself, in the same way that rhetoric textbooks aimed to prepare students for rhetorical performance. With that in mind it becomes less surprising that the early fragments of the Elements surviving on pot and papyrus have quite ‘wild’ versions of the text. This set of ostraka, in particular, should probably be read in this way: as an attempt to recreate something the writer had read or seen performed.

It is fitting that the earliest evidence for the Euclidean Elements is so enigmatic, so shakily related to the Elements themselves, and so, literally, fragmented. The text and its ideas would travel about as widely as it is possible for a cultural artefact to travel, but they would be much changed by the journey; and, what is more, it is not clear that they were ever simple, single and stable, even at the very beginning. Euclid was not a master but a muse, an inspiration: he did not just reveal facts but offered a set of tasks. His readers knew they could always go deeper and create more, because although the Elements had already done everything, everything was still to be done.

Hypsicles

The fourteenth book

Back in Alexandria, and still under Ptolemy III. Another legend, this one reported by Galen, the Roman physician.

Ptolemy III’s interest in collecting ancient books mounts to an obsession, a mania, and he has ships arriving at the harbour searched for texts that might be of interest to the Alexandrian library. On one occasion he receives, on loan from Athens, the precious scrolls containing the plays of Aeschylus, Sophocles and Euripides, depositing the fantastic sum of fifteen silver talents as security on the understanding that he will have copies made and return the originals.

He has copies made, indeed, and on the best papyrus. But it is those copies that he sends back to Athens, retaining the originals for his library. The Athenians can do nothing; they had accepted the silver on the condition that it would be theirs if the scrolls were not returned. They keep the copies, and they keep the money.

Ptolemy I (who learned there was no royal road to geometry) had abdicated in 284 BC in favour of his son, but the cultural institutions he started continued to grow, as did the great, the fabulous city of Alexandria. Its library became the largest collection of books in the world, an unequalled symbol of literary culture, a vast stocktaking of Greekness that surpassed anything to be found in Greece itself. The Ptolemies’ hunger for books became a legend; so did the lengths to which they would go to secure good copies of important works: as in the fabulous story quoted above, where Ptolemy III in the next generation paid a king’s ransom for the original Athenian texts of the great tragedies. As well as plays, histories and epics, though, the library had books on cookery, magic and fishing: no subject was excluded.

Meanwhile in mathematics, Euclid’s Elements remained the acknowledged toolbox of standard techniques and results, in which later Greek geometers used to discover all kinds of new things. Where Euclid had dealt with points, straight lines and circles, they dealt with the shapes made by the intersections of cones and planes, and with the solids formed when those intersections were themselves rotated about an axis: weird forms, surely close to the limit of what the human mind can conceive without the aid of algebra or digital visualisation. Yet they used Euclid’s terminology and relied on his propositions constantly. As well, they extended the Greek geometrical style itself in new ways that reflected the cultural preoccupations of Alexandria, with twists and turns, elements of surprise and sudden flashes of intellectual light.

Perhaps a generation or less after Euclid, Archimedes (c.287–212 BC) earned a reputation as the most brilliant of the Greek geometers, the most skilled at suspense, surprise, and showy unexpected results. One of his best-known surprises was that if you take a sphere and a cylinder with the same height and the same diameter, their volumes are related in the ratio of 2:3.

The great geometer of the next generation was Apollonius (c.262–c.190 BC); he shared his name, confusingly, with an Alexandrian poet who was head of the library. One ancient report says he studied in Alexandria with the pupils of Euclid (the passage is in fact the same one – the only one – that places Euclid himself in Alexandria). He systematised the study of conic sections – curves derived from slicing up cones – and adopted, too, the Archimedean manner in which beautiful results emerge as surprises at the end of long arguments.

The tradition continued. In 235 BC Eratosthenes, an astronomer and geometer, became head of the library (in succession to Apollonius the poet, in fact): an important moment for the integration of geometry into the culture of the Museum. Eratosthenes would become famous for deducing, correctly, the size of the earth from astronomical observations.

The icosahedron and dodecahedron, in a Renaissance woodcut.

Luca Pacioli, Divina proportione (Venice, 1509), plates XXII and XXVIII. Getty Research Institute, 47289. (Internet Archive/Public Domain)

One of the geometrical tricks and puzzles these geometers worked on was this. Take a dodecahedron and an icosahedron of the same size: that is, so that the two spheres into which the two solids would just fit are the same size. The dodecahedron’s faces are pentagons; the icosahedron’s are triangles. And it turns out – though you really wouldn’t expect it – that the pentagons and the triangles are the same size as each other: that is, the circle into which one of the pentagons would just fit is the same size as the circle into which one of the triangles would just fit. It’s a fun fact: not one that matters, but a good display of a geometer’s mental dexterity. It was admired enough to pass from hand to hand over several generations, and eventually to be annexed to the Elements.

It was a geometer named Aristaeus who first made the discovery, and published it in a book on the five regular solids which surely took its inspiration from the discussion that closed the Elements. Apollonius treated the problem in a work dealing solely with the dodecahedron and the icosahedron. Next, one Basilides of Tyre came to Alexandria, discussed the matter with a colleague and found Apollonius’ account wanting. Apollonius issued a new version of his text, in which he achieved the remarkable feat of showing that the volumes of the equal-sized dodecahedron and icosahedron form the same ratio as do their surface areas. Finally a man named Hypsicles took up the subject and put together all of what he found valid in the previous accounts.

This was in the middle part of the second century BC, perhaps 150 years after Euclid. Much is uncertain, but it seems Hypsicles was an astronomer as well as a geometer; in addition to a now lost book on the harmony of the spheres, and possibly one on numbers, he wrote a work on the rising and setting of the stars. It was in the style of Euclid and showed how to find (approximately) the rising time of a given point in the heavens – say, of a particular star – at a given place on the earth’s surface. It was also notable for being the earliest Greek text to divide the circle into 360 parts, a practice that derived ultimately from Babylonia.

Hypsicles responded to Apollonius’ revised book with a text of his own on the comparison of the same-sized dodecahedron and icosahedron. He provided new proofs for the main results: that their faces fit into the same circle, and that their volumes have the same ratio as their areas (make a cube of the same size, by the way, and its side and the side of the icosahedron will make that same ratio again). It was a short book, with just five propositions plus three subsidiary results – ‘lemmas’ – and one alternative proof.

Little is certain about how such things circulated, but it is clear that the treatise of Hypsicles, despite or perhaps because of its recondite subject matter, acquired some currency and was read, cited and admired. But it would suffer a curious fate. A later, anonymous hand attached it to Euclid’s Elements; where Euclid had written thirteen books, the treatise of Hypsicles was labelled ‘book 14’ and came to be transmitted as part of the Elements. There was some editorial modification at the same time, changing how the ‘book’ started and ended and also adding an extra proposition to Euclid’s own book 13 to strengthen the link. Almost incredibly, the ‘fourteenth book’ would remain a widely accepted part of the Elements for a millennium and a half.

The fantastic collection of books and people at Alexandria, and the mathematical tradition that was becoming associated with the city, interacted in some strange ways and produced some unforeseeable results. The rooms full of boxes full of scrolls made for some unexpected juxtapositions, odd misattributions and unlikely amalgamations. The Elements was part of that process, becoming a site of research, controversy and improvement even as it was transmitted from generation to generation.

Theon of Alexandria

Editing the Elements

Alexandria in AD 370, or thereabouts. The city remains: Greek, proud and beautiful. But the world is changing: temples are closing, churches are being built. The library is gone, and the Museum’s final generation of scholars is at work.

Theon is one of the scholars; his daughter works with him. They teach in the city: geometry, astronomy and philosophy. To teach, you need books, and they prepare new versions of the classic texts: Claudius Ptolemy on astronomy; the Orphic hymns; works on divination; and on geometry, Euclid.

These are long books. The scratch of reed on papyrus is day-long; fingers ache.

Theon comes to Elements book 6, proposition 33, and finds that the proposition is not quite complete. He adds a section, extends the result. And so Euclid’s Elements becomes a little longer and – he hopes – a little better.

Alexandria at its height had been the largest, richest, grandest city of the Greek-speaking world, the Ptolemies the patrons of every art and science. But like all dynasties they had their troubles, and after the Battle of Actium, from 31 BC Egypt was ruled from Rome, made into a province on the Roman model. The city was still rich and splendid; architecturally, it remained perhaps the finest city of the Mediterranean world.