The Book of Wonders

THE BOOK OF WONDERS

The Many Lives of Euclid’s Elements

Benjamin Wardhaugh

Copyright

William Collins

An imprint of HarperCollinsPublishers

1 London Bridge Street

London SE1 9GF

WilliamCollinsBooks.com

This eBook first published in Great Britain by William Collins in 2020

Copyright © Benjamin Wardhaugh 2020

Cover images: God, the Divine Architect © Bridgeman Images; The Friday Mosque © Gerard Degeorge / Bridgeman Images

Benjamin Wardhaugh asserts the moral right to be identified as the author of this work

A catalogue record for this book is available from the British Library

All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the non-exclusive, non-transferable right to access and read the text of this e-book on-screen. No part of this text may be reproduced, transmitted, down-loaded, decompiled, reverse engineered, or stored in or introduced into any information storage and retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of HarperCollins

Source ISBN: 9780008299903

Ebook Edition © August 2020 ISBN: 9780008299927

Version: 2020-07-10

Dedication

For my parents

Contents

Cover

Title Page

Copyright

Dedication

Prologue

I: AUTHOR

Alexandria: The geometer and the king

Elephantine: Pot shards

Hypsicles: The fourteenth book

Theon of Alexandria: Editing the Elements

Stephanos the scribe: Euclid in Byzantium

Al-Hajjaj: Euclid in Baghdad

Adelard: The Latin Euclid

Erhard Ratdolt: Printing the Elements

Marget Seymer her hand: Owning the Elements

Edward Bernard: Minerva in Oxford

Interlude

II: SAGE

Plato: The philosopher and the slave

Proclus Diadochus: Minerva in Athens

Hroswitha of Gandersheim: Wisdom and her daughters

Rabbi Levi ben Gershom: Euclid in Hebrew

Christoph Clavius: The Jesuit Elements

Xu Guangqi: Euclid in China

Blame not our author: Geometry on stage

Baruch Spinoza: The geometrical manner

Anne Lister: Improving the mind

Interlude

III: HERO

Petechonsis: Taxing and overtaxing

Dividing the monochord

Hyginus: Surveying the land

Muhammad Abu al-Wafa al-Buzjani: Dividing the square

Lady Geometria: Depicting the liberal arts

Piero della Francesca: Seeing in perspective

Euclid Speidell: Teaching and learning

Isaac Newton: Mathematical principles

Interlude

IV: SHADOW AND MASK

Mary Fairfax: Euclid and the straitjacket

François Peyrard: Manuscript 190

Nicolai Ivanovich Lobachevskii: Parallels

Maggie and Tom: The torture of the mind

Simson in Urdu: The Euclidean empire

His modern rivals

Thomas Little Heath: The true con amore spirit

Max Ernst: Euclid’s mask

Euclidean designs

Lambda: Curved space, dark energy

Epilogue

Notes on Sources

Select Bibliography

Index

Acknowledgements

About the Author

Also by Benjamin Wardhaugh

About the Publisher

Prologue

Alexandria. Alexándreia. The reign of Ptolemy, first of the Alexandrians. Perhaps the tenth year of his reign: a little after 300 BC.

Arrive by sea, the Egyptian sun on the water. Cross the harbour; enter the city. Building upon building. Through the Gate of the Moon and up the boulevard, the Canopic Way. White marble; dust and hammering: building work everywhere. The grandest of cities. You can drive your carriage up the streets if you want to. Paved streets and white-faced buildings. The sea murmuring.

To the crossroads; turn left onto the Street of the Sema: long and cool, catching the wind. Into the palace quarter. Temples; museum; library.

One of the workers in the famous cultural quarter is a man named Euclid. One of his books, the Elements of Geometry. When Ptolemy’s glorious Alexandria is dust, it will live.

For twenty-three centuries the Elements of Geometry has been changing the world. A compendium of facts about space and its properties – lines and shapes, numbers and ratios – it has drawn countless readers into its limitless world of abstract beauties and pure ideas. And it has been on the most incredible journey. Few artefacts survive the collapse of the culture that produced them; few texts survive the abandonment of the language in which they are written. The Elements has survived both. Indeed, it seems to have positively thrived on its transplantation into a series of fantastically diverse situations. Its very austerity seems to have enabled readers to find in it qualities that made it interesting to them, characteristics that gave it meaning in their time and place.

The sculptors of the west facade of Chartres Cathedral depicted Euclid, and the scholars of Abbasid Baghdad translated his book. An American artist turned his diagrams into art, and an Athenian philosopher wrote a commentary on them. The Elements was implicated in the Scientific Revolution: the fateful decision to read the book of nature as if it was written in the language of mathematics.

In Beijing, between August 1606 and April the following year, the scholar Xu Guangqi and the Italian Jesuit Matteo Ricci worked to translate the Elements, one of the books Ricci had brought with him from the far west, into the language of the Mandarin scholar. They struggled with terminology, with the structure of the text, with the very different assumptions each brought to its subject matter. They revised the text three times before they were happy to release it for publication.

From May to November 1817, on the other side of the world, Anne Lister set aside her mornings for – in equal proportions – arithmetic and Euclid. By the autumn she had worked through more of the Elements than most university graduates.

A thousand years before, at Gandersheim in Lower Saxony, the canoness Hroswitha wrote into one of her plays Euclid’s definition of perfect numbers. It formed part of Wisdom’s mockery of the emperor Hadrian, who was seeking to torture her and her daughters.

Again and again, new generations in new places have encountered the Elements and done new things with it. It has travelled through worlds that could never have been imagined by the Greeks who first wrote and read the text.

What does it mean for a book to live 2,000 years and more? To survive the wreck of the civilisation that produced it? To find readers again and again, in place after place and time after time? How vast a range of meanings do readers have to find in it? How vast a range of readers does it have to find?

Come on a journey and find out.

I

Alexandria

The geometer and the king

Alexandria, around 300 BC.

A dinner, say: a symposium, in the palace quarter, perhaps in the Museum. Ptolemy himself in attendance: general, hero, king, deity. And the talk touches on geometry: why so hard? Why is there no easier way? The geometer – a dusty man, but pert – answers: Majesty, there is no royal road to geometry.

Ptolemy snubbed is one of the irresistible stories. The man had been a childhood friend of Alexander the Great; one of his bodyguard. Maybe his illegitimate half-brother. He was a trusted general (the name is said to mean ‘warlike’): level-headed but capable of the grand gesture; a man of no nonsense.

He was one of the great survivors, too. In the twenty years of chaos that followed Alexander’s death, when many abler men died, Ptolemy played and won. Of all the successors who eventually carved up Alexander’s brief, continent-spanning empire, he founded the longest dynasty, the stablest country. He chose Egypt, and he never risked it for a larger realm. Fourteen Ptolemaic rulers followed him, until Cleopatra lost it all at the Battle of Actium 250 years later. The first king, then, of the last Egyptian dynasty. Basileus to the Greeks, pharaoh to the Egyptians. Inheritor of 3,000 years of Egyptian kingship and, yes, a god too. In 306 BC he defeated an attack on Rhodes so soundly that altars were erected to him and he acquired the title ‘saviour’. By 278 BC there were Ptolemaic games in his honour: four-yearly, like the Olympics.

Ptolemy I Soter.

Silver stater of Ptolemy I, 305–285 BC. Cleveland Museum of Art 1916.994. (Creative Commons/Public Domain, CC0 1.0)

The geometer, by contrast – a man named Euclid; Eukleídēs – is utterly obscure, historically speaking. The story about the ‘royal road’ is moonshine, sadly; it is also told about another geometer (Menaechmus) and another king (Alexander), and there is little reason to suppose it really happened. Even his dates – sometime around 300 BC – are the mere surmise of authors writing centuries after him. Unlike the exceptionally well-documented Ptolemy, Euclid left no biographical traces whatever. He founded no dynasty, built no palaces. His legacy was solely intellectual.

But what a legacy. The line of his students at Alexandria outlasted his life. His book outlasted his civilisation.

What was this city, that produced such a man and such a book? Alexandria was the right setting for the Elements of Geometry. It was Ptolemy’s greatest achievement. Alexander himself decreed the city, on the site of what had been a village and, like a dozen others, it bore his name. He never saw a stone erected, but Ptolemy took it for his capital, moving the Egyptian royal seat from Memphis. It was a Greek polis in a profoundly un-Greek world, a new foundation in a land where cities were 2,000 years old. Ptolemy did everything to make it splendid; it had an assembly, a council, its own coinage and its own laws. There were broad boulevards, colonnades, avenues of trees, street lamps. In 322 BC he kidnapped Alexander’s corpse and put it on display in his new royal city.

It was indeed the most splendid site for a city, at the meeting place of two continents, just to the west of the mouths of the Nile. It would be a major commercial port for centuries, a strategic military site until the Second World War. Ptolemy laid the foundations of the famous lighthouse: fortress and beacon, it would be one of the seven wonders of the world when it was done, 400 feet high and topped by a statue of Zeus. It stood for 1,500 years. Blessed with such a city, people immigrated from all over the Greek world, and Alexandria became not just notoriously big and splendid but notoriously crowded and cosmopolitan, with Greeks, Macedonians, Egyptians, Jews, Syrians and more, its streets teeming like ant heaps. Within a few generations it would have more than a million inhabitants.

As well as town planning, and the sheer erection of building upon building, Ptolemy involved himself in cultural policy: and with his characteristic effectiveness. To make himself a convincing Egyptian pharaoh, he indulged in sculpture to match, and devised a new cult of ‘Serapis’, a blatantly invented figure with a hybrid iconography. Like all his achievements, it endured: the temple, the Serapeum at Alexandria, stood for 600 years.

And to please the Greek mind and heart there were pageants, festivals, and a palace with tapestries the gods would prize. As one contemporary put it, Alexandria had ‘wealth, wrestling schools, power, tranquillity, fame, spectacles, philosophers, gold, youths, the sanctuary of the sibling gods … the Museum, wine, every good thing [one] could desire’.

All of which was invaluable in projecting Greek power and an idea of Greekness in a profoundly alien environment; in saying, this is what we do in the great Greek world. This is our right to rule.

And so, the Museum. The Mouseion: the shrine of the Muses. It was royally subsidised, with scholars in discipline after discipline. Their head was a priest of the Muses, and they included poets, grammarians, historians, philosophers, doctors, natural philosophers, geographers, machine-builders, astronomers, and of course geometers. It was partly Ptolemy’s own impulse, partly the creation of Demetrios of Phaleron, a famous pupil of Aristotle brought over from Athens to oversee the creation of the new institution. It had courts, covered walks and gardens, a dining hall and an observatory. The staff numbered perhaps forty, and they spent their time researching, writing and sometimes teaching. They held learned symposia, some attended by the king. They were a remarkable collection of people, sometimes compared a little sourly with the collection of animals that Ptolemy also founded: ‘well-fed bookworms, arguing endlessly in the Muses’ birdcage’. If there were bookworms, there were certainly books, too; the library at Alexandria would become the most famous in the world, though it seems to have been organised a little later, under Ptolemy’s son.

All of which is how the famous Greek mathematician ended up working in Egypt. Was Euclid another part of Ptolemy’s collection, someone brought in to swell the ranks of the Museum? It is not certain whether he was native to Alexandria or an immigrant, although at this early date in the city’s life the latter is much the more likely. An immigrant from where? His austere prose gives no hint of an accent: unlike Archimedes, in the next generation, who wrote in the Doric dialect of Syracuse.

What came to Alexandria in Euclid’s person (and perhaps in the persons of other mathematicians; it is not clear whether or not he was the only one) was a well-established tradition of Greek geometry. Greeks liked to have things to think about. They liked hobbies. Some Greeks raced chariots, some talked about philosophy, some occupied themselves with politics. From perhaps the late fifth century BC onwards, some did geometry.

What was it like? Perhaps it is clearest to think of Greek geometry as an outgrowth of the Greek love of talk, of disputation. For its geometry was nothing if it was not a performance.

Draw a line, a square, a circle. Reason out loud as you draw; play to the inevitable audience. From such beginnings the long-lived game of geometrical reasoning took shape. The figure of the geometer drawing in the sand remains part of the image of ancient Greek mathematics to this day: raking in the ‘learned dust’, as the Roman orator Cicero put it. He memorably evoked Archimedes as a man of ‘dust and drawing-stick’. (Though have you ever tried to draw a detailed diagram in dry sand? Pieces of clay, wax tablets or, for showing to a larger audience, wooden boards seem more probable.)

The number of Greek mathematicians was never very large, and they had to write their ideas down to preserve what they had found out about their lines and circles; there weren’t enough of them, it seems, for a purely oral transmission to stand a chance. So a genre was born: a special style of mathematical writing. That style would come to define mathematics in the West for more than two millennia, as constraining as any poetic metre, and as long-lived. Its components were the statement (of something to be proved); the diagram, with its points labelled with letters; and a chain of reasoning from things already known to things newly proved. That chain ended with the proposed, intended result, and the section – the ‘proposition’ – was rounded off with the note that ‘this is what was to be proved’: hóper édei deîxai; quod erat demonstrandum; QED. In some cases it was ‘what was to be drawn’. Here is an example:

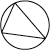
How to draw an equilateral triangle

Start with any straight line; call its ends A and B.

Now draw two circles, each with its radius equal to that line: one centred at A, the other centred at B.

The two circles will cross at two points. Pick one of them and call it C. Now join up A, B and C. They make an equilateral triangle.

Why?

Because of the way the distance from A to B was used to find C. C is that same distance from A, and C is also that same distance from B. In other words, all three of the triangle’s sides – AB, BC and CA – are the same length. So it’s an equilateral triangle. Which is what was to be drawn.

The same ancient sources that report when Euclid lived also report that there were written collections of geometrical learning in Greek by perhaps 400 BC: a century before him. They are quite informative about the subjects involved, and even some of the specific results and techniques. The written matter itself has not survived, though, throwing it all into doubt. There is a strong temptation to make up genealogies for mathematical ideas when real evidence is lacking. So yes, maybe the study of the circle was done by the Pythagoreans; likewise the work on numbers and their properties. Very probably the work on ratios was done by a geometer called Eudoxus early in the fourth century BC. Some work on the regular solids originated with another, named Theaetetus. The claim that there were, before Euclid, well-developed books called Elements of Geometry seems distinctly more doubtful.

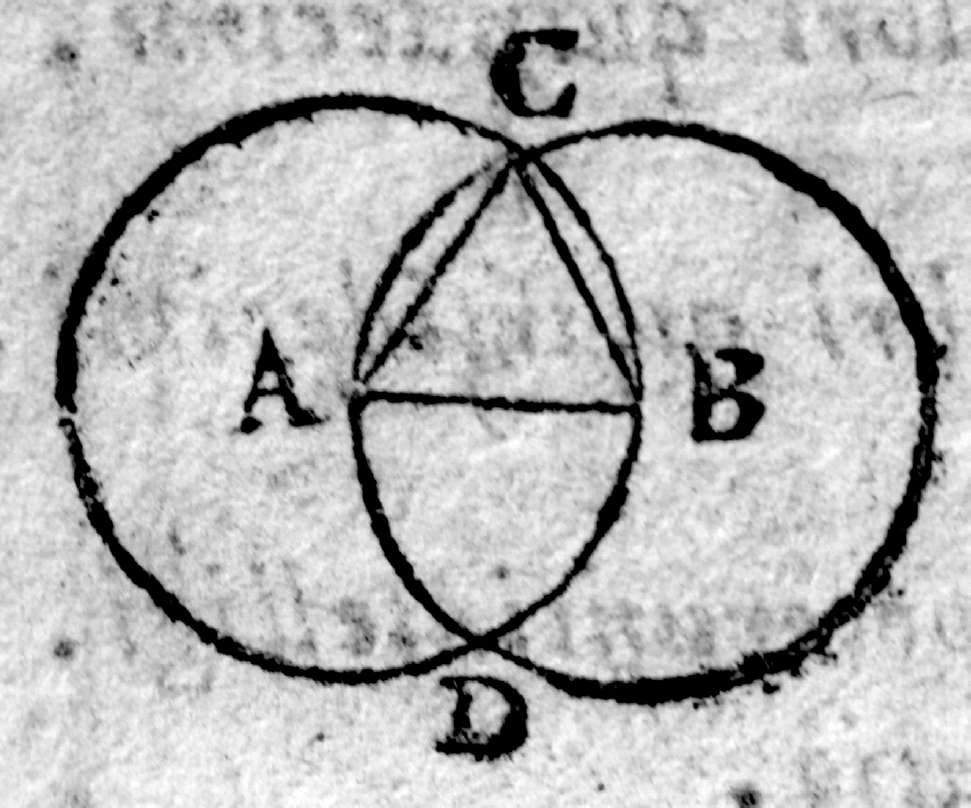
Constructing an equilateral triangle.

Christoph Clavius, Euclidis elementorum libri XV (Rome, 1574), fol. 21v. (Author’s collection. Image © Benjamin Wardhaugh)

What was Euclid’s role, then? He took all the easier material known to the Greek geometers of his day and put it all together in a single book. He organised it, both on the large scale and the small. Certainly he added some new matter of his own, though no one can now confidently identify what was new and what was not. Historians continue to argue – and they always will – about how much was compilation and how much composition in Euclid’s book. His was a work of collection, like Ptolemy’s; Euclid the Museum artefact became himself a curator, the Elements a smaller museum.

Yet this museum contained a world. It displayed the geometrical style of prose, in a relentless, ritualistic tramp of proposition after proposition: 400 of them, arranged in thirteen ‘books’ or chapters. Every verb was perfect, imperative and passive: ‘let a circle have been drawn’. There was something hypnotic about it; something infinitely calm. The book began with definitions: what was meant by a line? A point? A circle? It continued with the simplest manipulations of lines and shapes in two dimensions: how to draw different kinds of triangle; how to divide a line or an angle in two. The fact that, in a triangle, any two sides add up to more than the third. The Epicurean philosophers thought that last piece of geometrical information was ‘evident even to an ass’ since ‘if straw is placed at one extremity of the sides, an ass in quest of provender will make his way along the one side and not by way of the two others’.

Euclid did not care how obvious any of it was. He arranged and exemplified a toolbox of the basic techniques and results that he had inherited: ways of arguing, ways of proving; facts that geometers commonly assumed or used but seldom proved in full. At the end of the first book he placed ‘Pythagoras’ theorem’. Draw a triangle, with one of its angles a right angle. Using its shortest side as a base, draw a square, whose side is the same length as that side of the triangle. Repeat the procedure with the triangle’s two longer sides, so that you end up with three squares of different sizes, resting flush against the three sides of the triangle. Now, it turns out, the areas of the two smaller squares will add up to that of the larger one: a startling fact, not evident to any ass, which Euclid proved in his characteristically meticulous manner.

And so the ideas and the diagrams became harder and more complicated throughout the book. There were purely geometrical sections: a description of how to draw a regular pentagon or hexagon inside a given circle, for example. Parts of the book dealt not with geometry but with numbers and ratios, ranging from the most basic facts (‘if an odd number is multiplied by an odd number, then the product is odd’) to a procedure for finding the mysterious ‘perfect’ numbers, equal to the sum of their divisors.

Finally, Euclid turned to three-dimensional shapes. The last three books of the Elements – books 11, 12 and 13 – were concerned with spheres, cones and cylinders, with cubes and cuboids and with the regular polyhedra. These were beautiful solids whose faces were all the same regular polygon: triangles, squares or pentagons. There were just five regular polyhedra: the tetrahedron (four triangular faces), the cube, the octahedron (eight triangles), the dodecahedron (twelve pentagons) and the icosahedron (twenty triangles). He showed how to make such shapes, starting from, say, a given triangle or a given circle; he showed how to find their surface areas and their volumes. Euclid’s explorations in these final books were frequently ingenious, and sometimes applied an almost unbelievable amount of lateral thinking. Despite its gentle beginnings, and its incorporation of a lot that anyone could understand, the Elements as a whole was a virtuoso performance; a road that only the keenest of geometrical minds could follow all the way.

It added up to more than 20,000 lines of text in Greek. Euclid was careful, but he was no superman, and both joins and slips were sometimes visible. A few definitions (oblong, rhombus, rhomboid) seemed to have been carried across from older sources but never actually used. Quite a number of terms were used that were, conversely, not defined earlier on. Some words were ambiguous. A surprising amount was taken for granted about the properties of points and lines that Euclid never explicitly set out in his assumptions. Some propositions were merely special cases of others; some propositions were, strictly speaking, unnecessary because they were the mere logical consequences of others. But despite such wrinkles, the Elements was a fine, even an awe-inspiring monument to all that had been done in Greek geometry so far.

Euclid was by no means the author of just one book. The order of events is not clear, but it is certain that he wrote more. There were perhaps four other books on special topics in elementary geometry, and there were books on the applications of mathematics – to music, astronomy, optics and more – as well. In total nearly a dozen books are mentioned in the early evidence; eight actual texts survive, though most are disputed by historians.