Гравитация и эфир

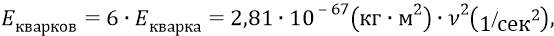
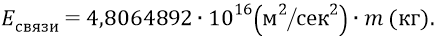
Соотношения энергий в этих «качелях» неведомы современным физикам. Однако физикам в этой их неопределённости не от чего оттолкнуться, и поэтому они измышляют разные варианты, не в силах их никак проверить. Одним из их предположений высказывается примерное равенство энергии кварков и «энергии глюонов», как тех «квантов энергии», которые скрепляют кварки внутри нуклона. Причём эти «глюоны» у физиков по своему статусу должны относиться к «безмассовым частицам», поскольку они движутся со скоростью света. Сам термин «безмассовая частица», доставшийся физикам тяжёлым грузом от СТО Эйнштейна, с точки зрения простой философии движения вещества в пространстве – смешон по своей сути. Мы, словно бы протестуя против этой въевшейся ржавчиной фиговины физиков, нагло приводим последнюю формулу, которую нарочно повторим ещё раз:

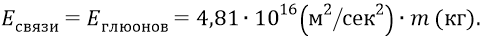
Здесь буковка «

» говорит именно о массе, выраженной в классических килограммах и говорящей о том – сколько килограммов «весят» эти «глюоны» физиков (несмотря на то, что эти «килограммы» – это, конечно же, их инерционная масса, зависящая от их скорости). Но поскольку и для физиков, и для нас очевидно, что эти «глюоны» движутся в пространстве только с единственной «скоростью света», то можно чётко вести речь о действительной (ньютоновой) массе этих частиц, выраженной в килограммах (кстати, в выражении закона всемирного тяготения, например, обе гравитирующие массы

, являясь по сути инерционными массами, выражены именно в килограммах).

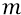
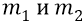
Так вот: имея нашу формулу, мы имеем и возможность напрочь отмести предположение физиков о возможном равенстве энергий кварков и глюонов в нуклоне. Потому что если эти энергии будут равны и составят, следовательно, величину половины энергии нуклона, добытой из опыта физиками

, то эти наши килограммы (

) зашкалят за ту величину, которая является табличной для физиков:

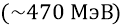
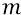
средняя «масса покоя» нуклона =

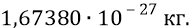
Напомним энергии нуклонов:

(соответствует «массе покоя»

),

(соответствует «массе покоя» –

).

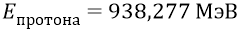
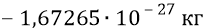
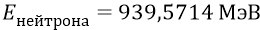
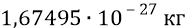
Тогда

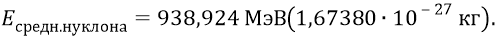
СТО Эйнштейна эквивалентит «килограммы» и «электронвольты» энергии частиц через свой любимый «коэффициентик» –

(он переводит килограммы сначала в джоули, а затем джоули преобразуются в электронвольты):

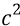
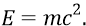
Этот «коэффициентик» как нельзя кстати пригодился в СТО именно для «безмассовых частиц» тогда, когда с помощью него находился импульс такой частицы. Мы же, в нашей классической квантовой физике, полностью свободны от СТО и пользуемся только нашими собственными формулами, во-первых, превосходящими по точности релятивистские формулы Эйнштейна, во-вторых, легко определяющими такие, например, характеристики как: скорость поступательного движения частицы (с чем у СТО возникают большие затруднения); собственные частоты вращения частиц (о чём СТО вообще не имеет ни малейшего понятия).

Итак, долго стоять у края очередной неопределённости (как ведут себя боязливые физики) мы не будем, но «нырнём» в какую-никакую, но нашу цифру, тем более, что ещё в главе 2-го тома «Неразгаданная тайна фотона» мы уже осторожно намекали о том, что собственная частота кварка в структуре нуклона должна иметь порядок

. Ни в коем случае не ошибаясь на порядки величин, но не ошибаясь даже в разы этих величин (но, может быть, лишь на проценты), мы выберем (для ровного счёта) суммарную энергию глюонов в «мгновенной» структуре нуклона, равную:

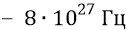
Тогда на долю 6-ти кварков будет приходиться (от средней энергии нуклона) следующая величина:

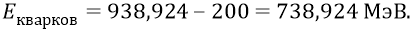
Энергия каждого из 6-ти кварков:

Но поскольку (с большой степенью точности, как мы уже упоминали выше) энергия поступательного движения кварка по орбите внутри нуклона равна 0,255 МэВ, то энергия вращательного движения кварка будет следующей:

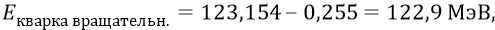
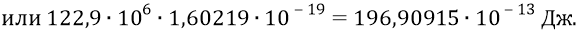
Тогда из нашей формулы определим собственную частоту вращения кварка, следующего поступательно по нуклонной орбите (при частоте там его «оборота» по орбите

):

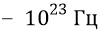
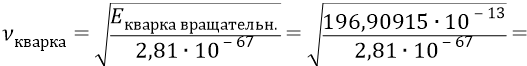
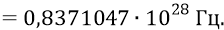
Далее, по графику

рисунка 14.4 второго тома Философии (глава «Философия нуклона») находим для энергии кварка

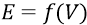
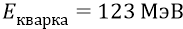
скорость его поступательного движения по окружности в конструкции нуклона:

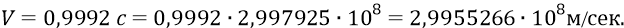
В соответствии с СТО Эйнштейна:

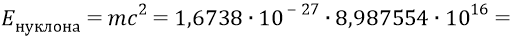
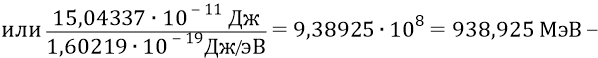
средняя величина между

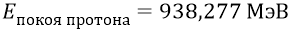
и

.

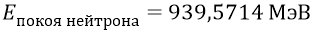
Итак, мы определили два фундаментальных параметра кварка-частицы в структуре нуклона:

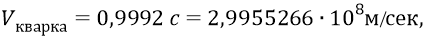
Мы утверждаем, что найденные величины параметров кварка в структуре нуклона могут отличаться от их истинных природных значений лишь на малые проценты номиналов величин.

Теперь вернёмся к глюонам. Неприглядным фактом для последователей-приверженцев СТО является то, что они, в угоду Эйнштейну, фактически продолжают называть эти материальные частицы какими-то противными здравому смыслу – «энергиями» (а ещё смешнее – «безмассовыми частицами»), вгоняя тем самым здравого школьника в полное недоумение. Мы же видим эти глюоны – как короткие потоки-импульсы квантов эфира (здесь, в нуклоне, – как кванты эфира высокочастотного его слоя, имеющие собственную длину волны, вдвое большую размера нуклона:

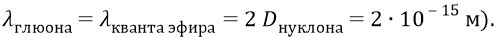
То есть каждый квант-частица эфира, из которых состоит глюон, делает на диаметре нуклона пол-оборота своей пространственной конструкции (а эта его конструкция, как мы помним, почти в точности повторяет конструкцию электрона).

Выразим теперь суммарную энергию глюонов (в каждое данное мгновение времени находящихся в полёте внутри нуклона, жёстко взаимодействуя при этом попарно – с каждыми двумя противоположными кварками и принимающими таким образом участие в общей инерции нуклона-частицы) в джоулях:

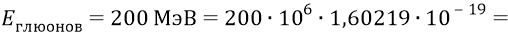
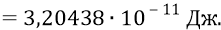
Тогда из нашей формулы для суммарной энергии глюонов найдём их ньютонову массу (чтобы никакой «безмассовостью» здесь не пахло):

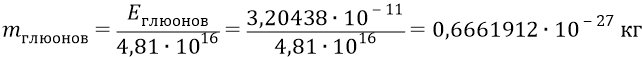
(напомним, что масса нуклона

).

Итак, в каждое мгновение времени, которое длится от момента излучения глюона кварком до момента приёма этого глюона «противоположным» кварком (нюансы этой «противоположности» смотри в главе 2-го тома «Философия нуклона»),

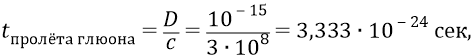
внутри конструкции нуклона действуют 6 пар глюонов (3 пары кварков «обстреливают» друг друга всего 12-ю глюонами). Следовательно, масса каждого из 12-ти глюонов составит величину:

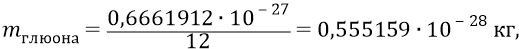
а его энергия

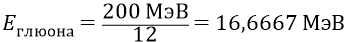
или

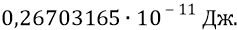
Проверим теперь величину энергии глюона по его классической массе, используя СТО Эйнштейна:

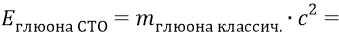
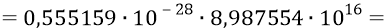
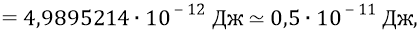
против наших

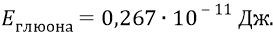
Мы видим, что СТО Эйнштейна почему-то завысила энергию глюона против нашей в

Это произошло потому, что СТО при высоких скоростях частиц занижает оценку их инерционной массы, а следовательно, оценку полной энергии частиц. Почему так происходит? Потому что СТО выбрала для высокоскоростных процессов неверную аппроксимацию инерционных масс частиц и их энергий с помощью корня Лоренца, стоящего в знаменателе формул СТО типа, например, следующих:

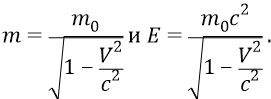
Здесь этот корень Лоренца уменьшает в квадрате значения величины

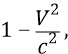
а следовательно, увеличивает в квадрате значения инерционных масс частиц

и их энергий

, при какой-то высокой скорости частиц

. Это не значит, что СТО с помощью корня ошибается именно на значение – «в квадрате» (на самом деле – ошибается для каждой данной высокой скорости

в своё определённое число раз, о чём мы скажем ниже). Но ошибка есть, и она существенна именно в области высоких скоростей частиц.

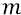
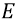
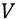
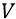
Однако даже и при этом корня квадратного недостаточно для того, чтобы этой теории вписаться в реалии высокоскоростных частиц. Для СТО надо было бы ещё круче уменьшать величину

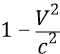
для того, чтобы она ещё круче увеличивала значения

и

при высоких скоростях. То есть надо было бы применить аппроксимацию между корнем кубическим и корнем квадратным. То есть надо было бы сделать так:

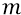
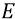
для высоких

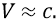
Тогда бы математический знаменатель был бы ещё меньше, а инерционные массы

и энергии

были бы выше и соответствовали бы действительности (как мы в том уверены).

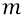
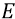
Заметим, что нигде ни в каких книгах и ни в каких статьях физиков и даже дилетантов мы не встречали подобного анализа теоретических формул СТО, какой мы делаем здесь, а также в главе «Философия нуклона» второго тома книги.

В главе «Философия нуклона» мы обращали внимание школьника на то, что приблизительное совпадение оценок масс и энергий двумя методами – нашим «классическим» и методом СТО – сохраняется лишь до скоростей частиц порядка

. Но уже начиная со скоростей порядка

оценка коэффициента увеличения инертной массы частицы, сделанная нашим «классическим» методом, более чем вдвое превышает оценку массы методом СТО. При скоростях же

величина нашей оценки на порядок превосходит оценку методом СТО. И наконец, для скорости частицы

наша оценка превосходит оценку массы методом СТО на 2 порядка величины (в 102,44 раза).

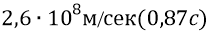
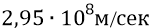
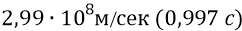
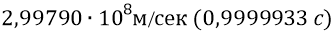
Именно поэтому, для того чтобы вписаться теорией СТО в нашу оценку энергии глюона

, этой теории надо было бы в её формуле

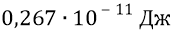
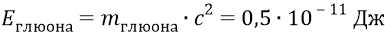
занизить массу

в 1,87 раза для того, чтобы получить оценку энергии

, сделанную нами.

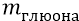
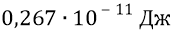
Ещё раз. Для того чтобы получить величину (в формуле

)

,

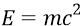
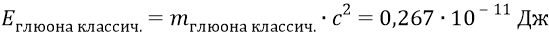
теории СТО надо сделать следующее:

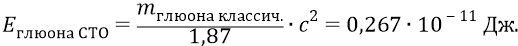
Итак, ещё раз. СТО при высоких скоростях частиц занижает оценку инерционных масс частиц, а следовательно, оценку их полных энергий. Каждый школьник это должен запомнить, а каждый физик-экспериментатор должен иметь в виду при постановке и проведении любых опытов с высокоскоростными частицами.

Но мы не нашли пока значение инерционной массы кварка, выраженной в килограммах. Помимо формулы полной энергии частицы, представленной суммой кинетических энергий поступательного и вращательного движения и уже приведённой выше по тексту, в главе «Масса физического тела» первого тома Философии мы вывели также чисто аппроксимирующую формулу для полной энергии частицы:

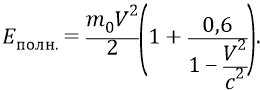
Из неё найдём инерционную массу кварка при его скорости

:

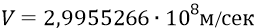
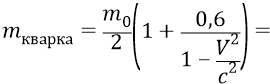
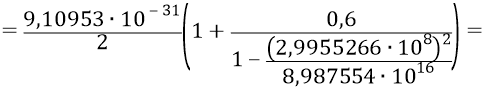
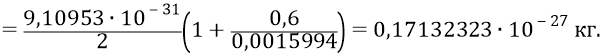
Тогда масса 6-ти кварков будет следующей:

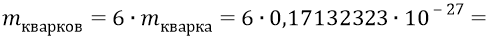
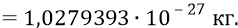
И если к этой массе кварков прибавить найденную нами ранее массу глюонов, то получим следующую «килограммовую» массу нуклона:

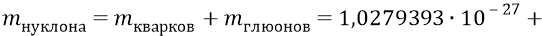
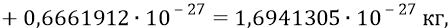
которая всего лишь в

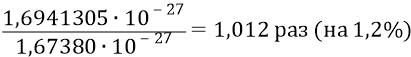
превышает классическую табличную массу нуклона.

И всё было бы хорошо, если бы последняя наша математическая формула не давала бы нам энергию кварка,

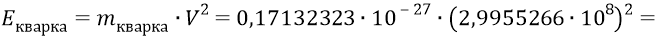
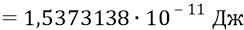
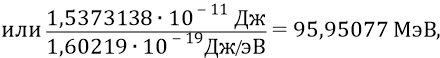
против нашего значения энергии кварка, принятого ранее –

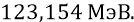
Какой цифре доверять больше? Мы больше обязаны доверять, конечно же, не чисто математической аппроксимирующей (подгоночной) формуле

с членами типа

, но чисто физической формуле, выведенной нами в главе «Масса физического тела» первого тома Философии:

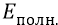
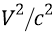
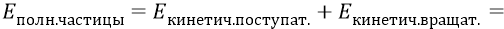
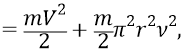
которая даёт, при прочих определённых параметрах кварка, его энергию

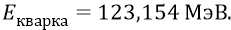
По поводу же некоторой нестыковки формул, которые дают разность в энергиях

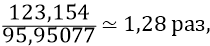
мы не будем особо страдать, тем более, что оценённые нами ранее эйнштейновские нестыковки подобного же рода составляют величину 1,87 раза. Любую чисто математическую аппроксимирующую формулу всегда можно подкорректировать реальным опытом. Было бы желание физиков.

Итак, «сухим остатком» из анализа некоторых параметров нуклона будем считать следующие ориентировочные цифры и утверждения:

инерционная масса и энергия нуклона принадлежит 6-ти кваркам и 12-ти глюонам его «конструкции»;

полная энергия кварка

;

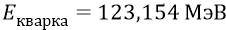
инерционная масса кварка

;

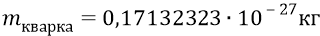
линейная орбитальная скорость поступательного движения кварка –

;

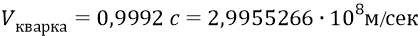
собственная частота вращения кварка вокруг оси симметрии его конструкции –

;

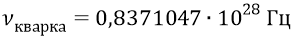
полная энергия глюона –

;

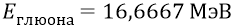
инерционная масса глюона –

;

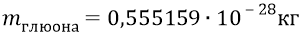
длина волны глюона –

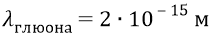
(определяется длиной волны квантов эфира высокочастотного слоя электромагнитного вакуума –

);

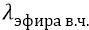
время пролёта глюона внутри конструкции нуклона –

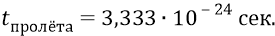
Полученные нами примерные характеристики нуклона можно и так и сяк крутить-вертеть, подгоняя их в будущих опытах под природную истину. То есть с ними уже можно как-то работать. Но физики до сих пор не имеют подобных характеристик, а следовательно, они не могут грамотно работать с нуклоном, а могут его только «бестолково» (извините – экспериментаторы) гонять (в «лице» протона) в своих, например, коллайдерах-приборах.

А также физики могут, размышляя о теме нуклонов, кварков и глюонов, измышлять всякие небылицы по поводу возможности существования так называемых «глюболов»-частиц, состоящих из одних лишь глюонов. Такие фантазии опасны потому, что отвлекают силы физиков на всякую ерунду. Уважаемые физики, Природа, создавая мир электромагнетизма, наверное, для того поделила все электромагнитные конструкции на класс «частиц» и класс «квантов» эфира, чтобы из «частиц» создавать далее сложную материю, но создавать с помощью квантов эфира. То есть кванты эфира, из которых состоят глюоны, Самой Природой (самой философией) не предназначены для того, чтобы из них создавать сложные конструкции (из них можно создавать только – короткие «линейные» – типа их короткой череды-потока в конструкции глюона).

«Хоть поверьте, хоть проверьте», но квант (частица) эфира отличается от кварков (электронов, позитронов и нейтрино) тем, что хотя и имеет такую же конструкцию как и у частиц (по типу двух ортогональных преонных колец), но активным в этой конструкции кванта является лишь одно кольцо из двух ортогональных. Второе же кольцо не активно потому, что оно одинаково равносильно реагирует на любое встречаемое им в пространстве кольцо частицы или кванта, одномоментно – и притягиваясь, и отталкиваясь этим встречным ему (любым) кольцом, то есть словно бы в результате – «никак его не замечая». То есть квант эфира хуже чем частица умеет, в результате сказанного, отклоняться в пространстве в ортогональном направлении, то есть хуже умеет искривлять свой прямолинейный путь в пространстве. Искривление же его пути при столкновении с частицей или квантом «лоб в лоб» крайне неэффективно. Поскольку такое столкновение между квантами эфира происходит с относительной скоростью равной двум единицам скорости света, то кванты эфира, налетая друг на друга, «почти не видят» друг друга в пространстве, проходя друг сквозь друга и отклоняясь в результате такого взаимодействия на чрезвычайно малую величину. Другое дело, когда частица эфира налетает на любую другую ортогонально к курсу этой другой, то есть с единичной взаимной скоростью света. Здесь взаимодействие будет максимально сильным – «резонансным».