Гравитация и эфир

Кварки в нуклоне потому имеют хорошую возможность закручиваться в конструкцию нуклона, что имеют оба активных ортогональных кольца. И поэтому тогда, когда кварк летит по орбите нуклона по касательной к этой орбите, то, имея очень большую частоту собственного вращения, он много-много раз подставляется своим ортогональным кольцом под поток тех квантов (глюонов), который следует фактически со стороны виртуального центра нуклона, а точнее – со стороны противоположного ему «антикварка». То есть, выражаясь терминами электродинамики, поле глюонов является для кварка магнитным полем, налетающим на кварк всегда с ортогонального направления курса его линейного движения по орбите. Квант-частица эфира тоже может так же отклоняться, как и кварк – тогда, когда её активное кольцо «смотрит» на виртуальный центр нуклона. Но она может так отклоняться (если случайно залетит в нуклон извне его конструкции – по касательной к орбите) только один раз за период своего вращения-волчка на орбите. Частица же (электрон-кварк) – подставляется под ортогональные глюоны дважды за период своей собственной частоты-волчка. Поэтому, для того чтобы получить «глюболу» с размерами нуклона, этим квантам потребовалось бы поле глюонов вдвое большее, чем для частиц-кварков, а такого поля в нуклоне нет. По поводу же возможной «глюболы» с очень большими размерами по отношению к нуклону, мы фантазировать не будем. А физики могут потренировать свой ум в соответствующих расчётах, а также в проведении соответствующих опытов.

Пусть в этом им поможет их мечта по сооружению, например, так называемого «фемтоскопа» – очень дорогостоящего прибора типа коллайдера. Сама задумка такого прибора – великолепна по своей мечте. Так, например, есть сведения о том, что в США лаборатория имени Джефферсона и Брукхейвенская лаборатория ищут средства и одобрение правительства на сооружение этого самого «фемтоскопа». Там исследователи собираются электроны сталкивать с поляризованными протонами и ядрами свинца. Но лучше будет, если будут одинаково поляризованы и протоны, и электроны. Причём не обязательно электроны разгонять (при этом) почти до скорости света, но наверное достаточно будет их разогнать (как следует из наших прикидок) до скорости

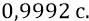
Причём для достижения максимальной эффективности прибора надо будет обязательно предусмотреть «покачивание» плоскости поляризации потока электронов относительно плоскости поляризации потока протонов. При этом «покачивании» очевидным будет резонанс – точное слияние этих плоскостей, когда выход количества полезных реакций резко возрастёт. Именно классическая квантовая физика заставит, наконец, исследователей применять чуть ли не во всех своих будущих опытах умные поляризаторы – как продукт резкого «поумнения» самих физиков тогда, когда они займутся фактически забытой ими классикой в деле исследования микро-мира вещества.

Вот и получается: вместо того чтобы строить очередную плавающую железяку типа авианосца, на фиг не нужную простому люду, лучше бы построили прибор – «фемтоскоп».

Сделаем теперь промежуточный вывод внутри темы о поиске плотности эфира (через поиск структуры нуклона):

когда тупые политики и те «серые» (тоже тупые), которые тех тупых дёргают за верёвочки, когда все они возьмутся, наконец, за ум, тогда будет интересно жить двум категориям любознательных людей: физикам и школьникам.

* * *

Только теперь, после того как определили энергию глюона, мы получаем возможность расчёта плотности распределения квантов-частиц эфира Метагалактики. Для этого будем пользоваться методом обратного счёта. Исходной цифрой здесь станет требуемая частота следования квантов-частиц в последовательной цепочке квантов, несущих энергию единичного глюона.

Ещё в главе «Неразгаданная тайна фотона» второго тома Философии мы обосновали и рассчитали фундаментальную величину всей современной квантовой физики – «элементарный квант действия»:

,

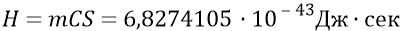
где m – ньютонова масса (количество вещества) кванта-частицы эфира, равная массе электрона – 9,10953∙

кг,

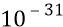
С – скорость света – 2,997925∙

м/сек,

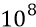
S – та дистанция, на которой происходит непосредственное взаимодействие кванта эфира и медленной частицы (в том числе – это тот путь, по которому квант эфира прошивает движущуюся частицу ортогонально к её курсу); в этой формуле величина S принята равной 2,5

м,

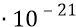
дополнительным параметром здесь является время взаимодействия частиц –

сек.

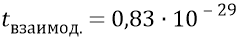
На рисунке 20.8 представлен процесс формирования глюона одним из кварков нуклона (кварк – излучатель 4) и далее – процесс передачи этого глюона от кварка 4 в сторону противоположного ему кварка (кварк-приёмник 1). Всю картину, представленную на рисунке, надо рассматривать как вертикальную, в которой ось Z – вертикальна плоскости XOY. Шести-угольная трасса-конструкция кварков 1–6 в нуклоне расположена вертикально плоскости XOY и сечёт эту плоскость ортогонально плоскости поляризации нуклона (кварки 5 и 6 находятся над горизонтом XOY, а кварки 2 и 3 – под горизонтом).

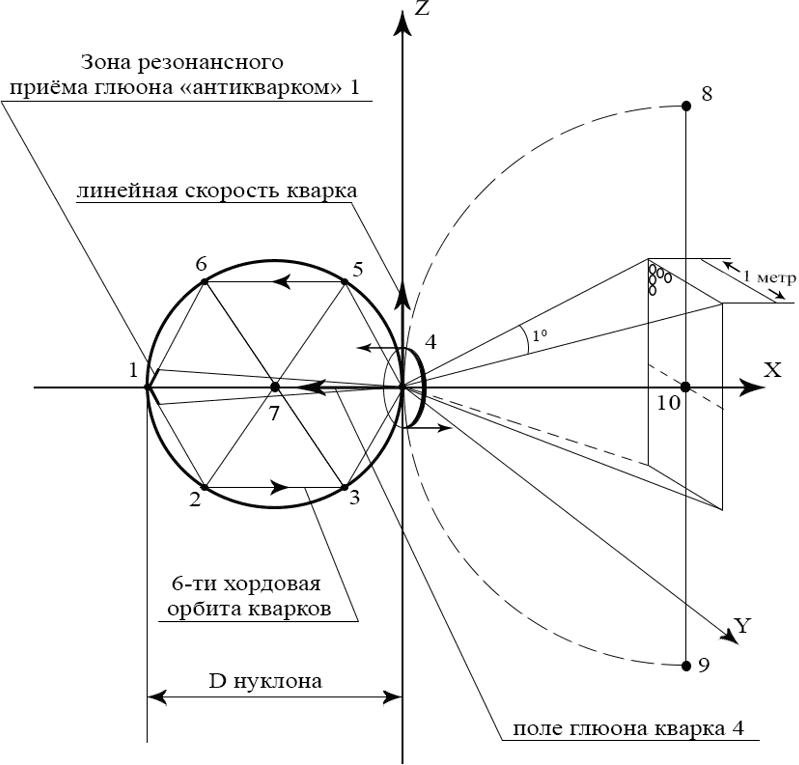
Рис. 21.8

В данное мгновение кварк 4 находится в вершине 6-ти угольника и переходит с хорды 3–4 на направление хорды 4–5. В это мгновение скорость кварка V касательна к той окружности, в которую вписан 6-ти угольник. Направление собственного вращения всех кварков, следующих по хордам, – левое (против часовой стрелки). Направление движения кварков по 6-ти хордовому пути – тоже левое (против часовой стрелки). Поскольку в данное мгновение активное кольцо кварка 4 (на рисунке показано только одно кольцо из двух – ортогональных) строго вертикально, то кварк принимает эффективно резонирующие с ним кванты эфира с узкого пространственного «конуса» с раскрывом в

и центральной осью конуса, совпадающей в это мгновение с направлением оси X (направление 4–10). Плоскость собирания квантов эфира в этом конусе (ортогональную оси X), вообще говоря, можно располагать на любом удалении от кварка 4. Но поскольку нашей задачей является вычисление плотности распределения квантов эфира (которая нормирована к одному кубометру), то сразу же отнесём эту плоскость от кварка на то расстояние r, на котором размеры сечения «конуса» будут равны квадратному метру. И поскольку эта плоскость видится со стороны кварка под углом

то мысленно проведём на расстоянии r радиусом 4–10 окружность длинной L, вдоль которой, следовательно, будут укладываться одна к одной площадки в 1

. Всего таких площадок вдоль окружности будет 360 штук (по одному градусу дуги L на площадку):

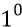
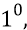
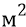
откуда расстояние r (4–10),

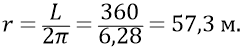
Если мы теперь на этой площадке разместим (одна к одной) конструкции квантов-частиц (они имеют размеры такие же как у электрона –

), то можем вычислить количество квантов-частиц, с их плотностью распределения на площадке – «одна к одной», которые будут постоянно собираться из эфира по конусу с раскрывом в

, параллельно к плоскости поляризации кварка 4. При любых вращениях кварка 4 (при вращениях – как вокруг собственной оси, так и по хордовой орбите внутри нуклона, эту плоскость можно считать как бы «приклеенной» к плоскости поляризации кварка. То есть она будет быстро вращаться вместе с вращением кварка, собирая кванты в конусе каждый раз с того направления, куда в данное мгновение будет «смотреть» кварк 4.

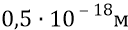
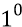
Итак, на площадке одного квадратного метра разместится следующее количество квантов эфира:

квантов эфира.

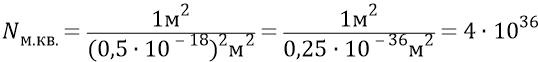
Эта цифра пока ещё ни о чём не говорит, то есть никак пока не говорит о возможной реальной плотности квантов эфира, размещаемых в реальном вакууме на площади квадратного метра. Она, эта цифра, должна быть в результате той, которую мы «сошьём» с энергией глюона, излучаемого квантом 4 из собираемых им квантов конуса. Если на площадке квадратного метра расположен единичный квант (из их количества там

штук), то это не значит, что этот квант «сейчас» полетит точно на кварк 4. Квант площадки, как реальный квант-частица эфира, оказавшийся в данное мгновение в пределах этой площадки, может лететь в левую сторону от неё – в направление кварка – по любому лучу левой полусферы радиуса r. Поэтому сейчас нам придётся подсчитать вероятность того события, когда квант площадки, двигаясь справа-налево, попадёт точно на размер кварка.

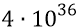
Площадь левой полусферы 8–4–9 с её осью 4–10 (формула площади полной сферы S=4π

:

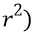
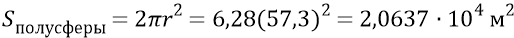
Количество частиц, которые можно разместить на этой полусфере «одна к одной»:

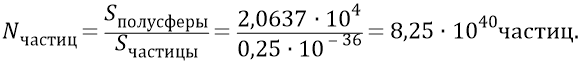
Итак, если предположить, для начала, что любой из квантов эфира площадки S должен попадать точно по центру масс кварка 4, то вероятность такого события для каждого кванта эфира площадки будет:

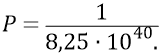
Но, кроме того, для эффективного взаимодействия кванта и кварка 4, их поляризации должны совпадать (в данном случае их поляризации должны быть «вертикальными»). Это уменьшает общую вероятность эффективного взаимодействия кванта и кварка вдвое. И, кроме того, из всех квантов площадки S нам годятся только те кванты-частицы, которые совпадают с данным кварком (4) по знаку заряда этого кварка. Если этот кварк, например, – электрон, то мы отбираем с площадки S только «отрицательные» кванты, которые, взаимодействуя с электроном, излучатся «из него» квантами «отрицательного» поля электрона. Поэтому вероятность нужных нам квантов площадки S придётся ещё раз ополовинеть.

Но ещё и кроме того: любой квант площадки S обязан подлететь к кванту 4 «кольцо к кольцу» по своей пространственной фазе. Причём они должны встретится именно соответствующими сторонами из колец (конструктивные вопросы эффективных взаимодействий электромагнитных квантов на их преонном уровне, в данном издании нашей книги мы пока не рассматриваем; но заранее утверждаем при этом, что, например, электрон только тогда может эффективно провзаимодействовать с налетающим на него «отрицательным» квантом, когда этот квант налетает только одной определённой стороной своего кольца; если же он налетит, хотя и точно по цели, но другой стороной кольца, то из такого кванта не получится поля электрона, но он для последнего будет представлять обычный эфирный квант, никак не взаимодействующий с электроном). Итак, по этому признаку нам придётся уменьшить вероятность отбора нужных квантов с площадки S для поля кварка 3 ещё в 360 раз. Итого вероятность отбора квантов для кварка 4 определится величиной:

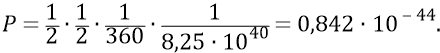
Обращаем внимание, что при вычислении данной вероятности мы не учитываем возможное уменьшение последней цифры ещё в 360 раз (за счёт распределения возможного углового положения самого кольца кварка 4), поскольку это его вертикальное положение у нас изначально нормировано. То есть при любом повороте кольца кварка 4 от вертикали, вместе с ним будет смещаться площадка S по периметру L (мы об этом уже говорили).

Итак, уже сейчас – на этом этапе, мы можем в первом приближении оценить плотность распределения квантов реального эфира на площадке одного квадратного метра, которая должна быть такой, что умноженная на полученную вероятность, должна дать значение не менее единицы:

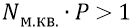
И поскольку природа вещей не любит излишеств, то выберем значение N равным:

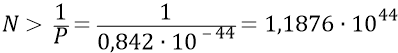
Однако (для ровного счёта) мы округлим цифру количества частиц на площадке квадратного метра в меньшую сторону:

частиц

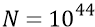
на площадке квадратного метра, со сторонами из количества частиц по каждой стороне квадрата (частиц с собственными размерами

), уплотнённых по расстояниям между их центрами масс – «один к одному» –

частиц.

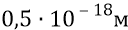
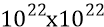
Шаг центров масс частиц по стороне квадрата 1 м:

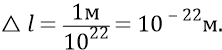
То есть получили уплотнение частиц в эфире настолько сильным, что на размере-диаметре одной частицы (

размещаются

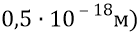
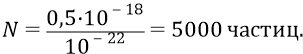
В такую возможную плотность эфира трудно поверить и к ней трудно привыкнуть. Однако она может испугать кого угодно (из физиков), но только не нас. Кстати, Максвелл ещё полтора века тому назад представлял себе эфир в виде сцепляющихся друг с другом «колечек». Человек умел думать. Ещё раз убеждаешься в том, что все великие учёные имеют могучую интуицию, которая не позволяет им делать ошибок не в их «точной» теории, но в их философии.

Эту плотность эфира мы теперь попробуем «приспособить» к значениям энергий частиц, довольно точно рассчитываемым классическим методом исследования процессов.

Итак, в каждое мгновение времени хотя бы одна частица на площадке квадратного метра (из

других там частиц) уже имеет те характеристики и то направление её движения, которые позволят ей двигаться в узком конусе

и через некоторое время точно ударить по кварку 4. В следующее мгновение времени тоже самое будет готова делать следующая (одна) частица из следующего квадрата (1

), расположенного (справа) от первой площадки на шаг расстояния между площадками квадратных метров (шаг «горизонтальной» плотности распределения частиц):

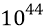
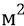
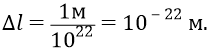
Таким образом, на кварк 4 всегда будет налетать поток – череда последовательных частиц, следующих одна за одной через период времени:

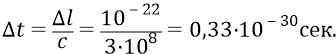
Частота следования квантов-частиц эфира в этом потоке:

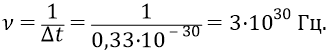
Все частицы этого потока будут заведомо эффективно взаимодействовать с кварком 4: так, что после кварка, вступив с ним в пространственный резонанс, они превратяться в поле этого кварка. Мы со школьниками уже знаем, что поле – это поток квантов, направленных в пространстве (или – «направленный поток квантов»).

Здесь же отметим важное обстоятельство. Мы утверждаем, что в пространственном резонансе двух электромагнитных частиц они обе («долго» взаимодействуя друг с другом своими преонными полями, при их встрече с согласованнымим характеристиками) очень сильно подстраивают положения их конструкций друг под друга. Чем тяжелее частица (чем она инерционнее), тем легче она подстраивает «под себя» встречаемою частицу. Кварк нуклона на много порядков «тяжелее» кванта – частицы эфира. Поэтому именно кварк подстраивает под себя каждый квант эфира. И поэтому после кварка квант эфира полетит именно туда, куда «смотрел» кварк плоскостью своей поляризации в момент их взаимодействия. «Коэффициент усиления» (коэффициент «направления» в пространстве) кварком кванта эфира вполне может достигать величины двух-трёх порядков. То есть если кварк принимал поток частиц из конуса

, то после себя он направит кванты своего поля под углом в одну тысячную градуса, что позволит этим квантам попадать по центрам масс точно на противоположной кварк 1, с которым все они заведомо согласованы в конструкции нуклона по своим фазам (вращаясь в пространстве на пути диаметра нуклона на пол-оборота, то есть на

, они имеют рассогласование по фазе их вращения не более одного градуса; смотри чуть ниже).

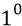
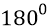
Теперь рассмотрим взаимную «геометрию» кварка 4 (с его полем-глюоном, состоящем из направленного им потока квантов – частиц эфира) и противоположного кварка 1. Зону резонансного приёма антикварком 1 глюона, излучённого кварком 4, мы определим по расфазировке каждого кванта-частицы состава глюона на пространственный угол

Мы утверждаем, что в конструкции нуклона каждый квант-частица эфира из состава поля глюона делает вдоль диаметра нуклона половину своего пространственного оборота («рисует» в пространстве половину своей длины волны). Поэтому, при расфазировке между противоположными кварками на

, расстояние этого поворота, преодолеваемое по диаметру со скоростью света, составит величину:

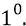
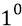
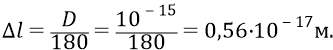
Время прошивания этой зоны квантами эфира структуры глюона:

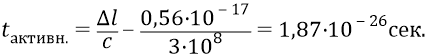
В течение этого времени каждый из квантов эфира, излучённый кварком 4 и подлетевший к кварку 1, имеет возможность эффективно (резонансно) взаимодействовать с кварком 1.

За это же время кварк 1, двигаясь почти со скоростью света по хордам 6–1 и 1–2 в районе вершины 1 6-ти гранника, проходит расстояние:

·

(эта дистанция в районе точки 1 отмечена на рисунке 20.8 жирными отрезками).

А также, за это же время на этой дистанции кварк 1, вращаясь с собственной частотой

делает следующее количество оборотов:

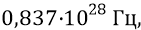
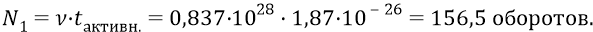
На каждом таком обороте кварк 1 подставляется активной стороной своего кольца под кванты эфира (кванты в структуре глюона) поля кварка – излучателя 4 (мы говорим: кварк 1 «смотрит» на кварк 4).

Ещё раз. Поскольку каждый квант эфира, излучаемый кварком 4, достигая кварка 1, заведомо точно сфазирован по своей пространственной фазе (на угол плюс минус

что является первичным условием для наших расчётов), а также поскольку этот каждый квант эфира пересекает резонансную зону кварка 1 достаточно «медленно» (за

то, следовательно, в этот промежуток времени он продолжает оставаться точно сфазированным со всеми 156,5 теми положениями кварка 1, когда в этих положениях последний на каждом из своих оборотов точно «смотрит» на кварк – излучатель 4.

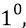
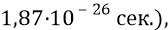
Итак, за время резонансного взаимодействия между двумя противоположными кварками каждый из квантов эфира, излучённый кварком – излучателем, достигает кварка – приёмника 1 и эффективно взаимодействует с ним, поворачивая этот кварк – приемник на соответствующий угол, а в сумме – на угол его поворота с одной хорды на другую – следующую (этот угол в 6-ти граннике равен

).

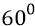
Фактически мы только что «разбили» единый глюон кварка 4 на 156 квантов – «импульсов» эфира (примем эту цифру – 156), заполняющих структуру «полного» глюона. Таким образом, можно считать, что каждый из 156-ти квантов (излучённых кварком 4) должен обладать следующей энергией (при том, что каждый из этих 156-ти квантов может содержать сразу несколько единичных квантов эфира):

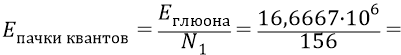
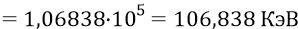
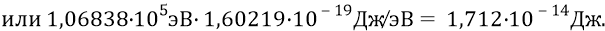
Теперь подойдём к этому же процессу формирования глюона из квантов эфира с чисто энергетической стороны. Формула Планка (с нашим в ней значением «кванта действия – Н) говорит о том, что нам необходима следующая частота следования квантов в пачке – структуре глюона:

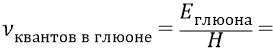
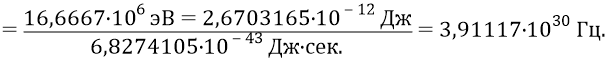
То есть период следования квантов эфира в структуре глюона должен быть следующим:

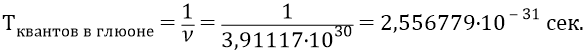
Такой частоты исследования квантов эфира с таким их периодом было бы достаточно, если бы эти кванты излучались кварком 4 в сторону кварка 1 непрерывным потоком – «частоколом». Однако кварк 4 вращается с собственной частотой

и периодом Т =

. При таком вращении он излучает в сторону кварка 1 кванты: не в течение всего его периода вращения, но только тогда, когда он «смотрит» в сторону кварка 1, движущегося в активной зоне приёма им квантов кварка 4. Но поскольку в одном глюоне 156 пачек квантов эфира (за период излучения-приёма глюона оба кварка 4 и 1 «смотрят» друг в сторону друга 156 раз), то частота излучения этих пачек будет эквивалентна частоте вращения кварка, умноженной на 156:

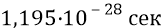
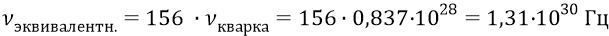
Мы видим, что оценка частоты потока квантов в структуры глюона сделанная разными методами, «крутится» около одной и той же цифры –

.