Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

А вообще в музыке для этого явления существует специальный термин:

э н г а р м о н и з м.

Это только на первый взгляд термин отпугивающе непонятный. Но зрение ума ведь не раз приводило нас в глубины смыслов всяких терминов, – и смыслы озарялись светом понимания.

Энциклопедия:

Энгармонизм – от греч. en – «в» («внутри») и harmonia – гармония.

Гармония – со/звучие, со/существование в со/гласии.

В ТОНАЛЬНОСТИ могут сосуществовать два возможных её проявления: бемольное и диезное. Тональность внутри тональности.

Бемольное проявление – к НИЗУ, плотности, плоти, сгущению, затемнённости. Диезное – к ВЫСИ, пространству, свету.

Как и мы: то в заботах земных ( о теле и его комфорте), то в душевных порывах ввысь, к духу, умозрениям всяким… Но при этом мы остаёмся собою. С двумя возможностями проявлений себя. К тому же эти возможности мы можем проявлять «мажорно» и «минорно» («мажор» – «большой», «минор» – «малый»; разный размах, масштаб, мера активности…).

Энгармонизм позволяет быстро и даже неожиданно поменять направление модуляций – от бемольного к диезному и наоборот. Ведь любую бемольную тональность можно тут же превратить в диезную, а диезную в бемольную, – что заставит трезвучия вращаться по-новому, в новых направлениях. Достаточно вдруг увидеть новым взглядом за бемолями диезы, а за диезами – бемоли.

Обязаны ли бемольные тональности быть привязанными только к направлению ВНИЗ, а диезные – к направлению ВВЕРХ?

Вовсе нет!

Любое земное дело можно делать с душой и смыслом. Это возвышает земные заботы. Так домостроительство превращается в искусство архитектуры, заботы о еде – в искусство кулинарии, заботы о комфорте – в искусную инженерию и т.п. Высокие замыслы – продукты наук и искусств – воплощаются, реализуются в предметах, которые делают наше земное существование более комфортным и исполненным красоты.

В космосе тёмную материю пронизывают фотоны, а в центрах сияющих галактик – сверхплотные чёрные дыры…

В каждом человеке – женские и мужские гормоны (вещества, определяющие пол; дело в том, какие «победили»).

Взаимопроникновение противоположностей.

Хорошо знакомая всем и ныне невероятно популярная древнекитайская эмблема-символ ИНЬ и ЯНЬ – об этом.

Вот и бемольные тональности могут подниматься ввысь, по о б р а т н ы м квинтам (обращённым), иначе – по квартам:

Рис. автора.

А диезные тональности могут спускаться вниз, тоже по квартам:

Рис. автора.

Если ты проявил любопытство экспериментатора и проиграл всё это на пианино, у тебя, скорее всего, могло возникнуть чувство какого-то несовершенства, незавершённости: словно модуляции не совсем настоящие, переход в тональности слишком быстрый и зыбкий, – не успеваешь его ощутить. Может быть, в данном случае не хватает второго обращения трезвучия?

Как бы там ни было, но в музыке субдоминантовая функция, которая связана с квартой, используется именно для передачи ощущения незавершённости в музыкальном предложении.Когда предложение оканчивается неопределённо, с сомнением, такое окончание называют н е с о в е р ш е н н ы м кадансом (от лат. cado – «оканчиваюсь»).

Кварты у нас вообще показывают равновесие в октаве. Они не желают выходить за её пределы. А значит, и в тональности они будут «голосовать» за старую добрую Тонику. Субдоминантовая функция кварт – за неё. Ну могут кварты-Субдоминанты «выглянуть в окошко» другой тональности, однако предпочтут остаться дома, к Тонике поближе:

Рис. автора.

И даже в этом примере ты ещё не услышишь окончательного совершенства. Потому что… как же без Доминанты? Зачем тогда и в окошко выглядывать, если не манят бескрайние просторы, само бесконечное пространство, – воздух, солнечный свет, космическое небо?.. С квинт-Доминант и жизнь-то начинается! Да, у нас есть дом, но мы выходим из него – чтобы вернуться.

Получается что-то вроде этого:

Рис. автора.

Модуль-октава и функциональный модуль нашей жизни.

Здесь вот что интересно: появление в аккорде доминантовой функции того же звука, что и в тональности, в которую мы «выглянули в окошко» (из Фа в Си-бемоль). Этот звук устанавливает связь с поманившей тональностью (Си-бемоль). Но он возможен только если доминантовая функция явится нам не трезвучием, а четырёхзвучием (ДО-МИ-СОЛЬ-СИ-бемоль и его обращения).

Можно говорить и «четырезвучие» (так у Римского-Корсакова).

Есть один важный нюанс в обращениях четырезвучий. В этих обращениях появляется д и с с о н а н с – интервал с е к у н д а (она же – обращённая септима по краям начального аккорда).

А как же не появиться этому диссонансному настроению?! – Мир манит, а тебе велено – домой! Квинты-доминанты рождены для бесконечности, а тут – конец свободе. О г р а н и ч е н и е, границы. Отдельность, отделённость от бесконечности. Вот она, дискретность. Так велит модуль-октава. И вписанная в этот модуль ТОНАЛЬНОСТЬ. Мир отделённых друг от друга форм. Мы ведь, телесно, – тоже отдельная форма. Лишь мысль странствует бесконечно.

Человеческая мысль добралась и до космических бездн, а жить нам – на Земле.

Хотя… Пространство проникает в нас беспрестанно. Мы вдыхаем воздух ( вдыхаем небо! его кислород – в каждом нашем сосуде, в каждой клеточке ), наши тела – по большей части вода (а для многих земных существ она – пространство жизни), магнитные потоки пронизывают нас. Мы не видим этого круженья, этой связности, но что же это, если не квинты-доминанты?

Совершенство непременно требует доминант связности даже в дискретных формах. Сложно?

А в модуле-октаве всё это есть. И в каждой тональности это есть. И мы столько раз это видели! И слышали!

Ещё чуть-чуть об аккордах.

Да, выходит, что они бывают не только трезвучиями, но и четырезвучиями. И даже пятизвучиями. Шестизвучия не принято использовать. Они при вращении-обращении производят слишком много диссонансов – хаос.

Итак: три – четыре – пять.

Три эти числа и ограничивают возможности аккордов.

Тебе эти числа ничего не напоминают? – Например, из математики, из геометрии…

Рис. автора.

Египетский треугольник – дитя окружности, поделённой на 12 частей.

Египетский треугольник, имеющий связь с Золотым сечением, с квинтами.

?

Опять эта симметрия самоподобия проникает всюду. И ведёт к вращательной симметрии пространства…

Пятизвучие называют нонаккордом, потому что оно вписывается в интервал нону.

Четырезвучие называют септаккордом, потому что оно вписывается в интервал септиму.

По аналогии трезвучие хочется назвать квинтаккордом, потому что оно вписывается в квинту. Но его так не принято называть. Можно перепутать с квинтсекст-аккордом, обращением септаккорда, четырезвучия.

Просто основное трезвучие. И всё.

Оно может явиться нам в виде четырёх звуков: ДО-МИ-СОЛЬ-ДО. Но всё равно останется трезвучием, так как его прима и октавный звук – по сути, один и тот же звук, только удвоенный. Поскольку такое трезвучие охватывает всю октаву, его называют полным тоническим трезвучием.

Когда музыкальное предложение заканчивается тоническим трезвучием, мы слышим совершенный каданс (или совершенную каденцию).

Всё согласовалось: модуль-октава, в этом модуле – тональность, в тональности – главные функции: тоника Т – субдоминанта S – доминанта D – и возвращение в тонику T. Полнота проявлений земного и небесного, предметного и пространственного миров, дискретность и связанность. Совершенство!

Вот интересно, если ТОНАЛЬНОСТЬ не решится поддаться смелым призывам Доминанты отправиться в головокружительную бесконечность по квинтам со сменой своих образов, а предпочтёт всё-таки остаться дома, в своём модуле-октаве – поддавшись влиянию Субдоминанты (субдоминантовой функции), которая всегда за Тонику, за стабильность, – будет ли у неё при этом возможность изменяться, модулировать?

Я думаю, что мы похожи (мы с ТОНАЛЬНОСТЬЮ). Знаешь, чем? – Внутренним сходством. Мы можем изменяться в н у т р и себя, то есть тоже модулировать, но исходя из своих внутренних ресурсов, разных способностей.

У всех живых существ способности зашифрованы в генах.

(Ты, наверное, знаешь в общих чертах, что гены – это такие вещественные образования в нашем организме, которые в определённом порядке упаковываются в другое красивое вещественное образование в виде двойной спирали под названием ДНК, а ДНК упаковывается в хромосомы, те – в ядра клеток, а из клеток состоим мы.)

Гены передаются нам по наследству, от родственников (греч. γένοζ – «род»).

У любой тональности всегда найдётся как минимум шесть ближайших родственников, чьи гены в неё упакованы (как у нас ближайшие шесть родственников: мама, папа, две бабушки, два дедушки).

Об этом можно почитать в чудесной и умной книге, написанной всемирно известным русским композитором Николаем Андреевичем Римским-Корсаковым. Называется эта книга «Практический учебник гармонии». Этот учебник написан для студентов Санкт-Петербургской консерватории, но написан так ясно, что при желании любой пытливый ум сумеет постичь смысл его содержания.)

Строями Р.-К (Римский-Корсаков) называет тональности. Названия мажоров пишутся с прописных букв (больших, мажорных), а названия миноров – со строчных букв (малых, минорных).

Помещена эта страничка в раздел «Модуляция».

Приведённые примеры показывают, что практически каждый звук октавы-тональности готов проявить себя как родственная тональность со своей неповторимой особенностью-способностью. Каждый музыкальный ген может прийти в активное состояние, и тогда основная тональность, изначальная, почувствует в себе изменение – то есть осуществление модуляции. Какие «гены» будут активированы и задействованы – зависит от неповторимой мелодии. Как применять определённые аккорды для гармонизации мелодии – об этом тоже пишет в своём учебнике Р.-К.

Мелодия влечёт за собою и модуляции в родственные тональности.

И эти модуляции тоже происходят благодаря способности аккордов вращаться-обращаться, связывая между собою нужные тональности.

Не обязательно будут задействованы в с е возможные тональности, нет.

Неповторимая мелодия изольётся из души и сделает выбор.

В этом есть свобода и непредсказуемость.

Но есть и правила взаимоотношений между Тоникой, Субдоминантой и Доминантой в тональности – распределение функций, обязанностей согласования действий. Как же совместить свободу и непредсказуемость с правилами поведения?

Есть один секрет.

Он заключается в том, что к а ж д ы й аккорд каждой родственной тональности присоединяется к Субдоминанте или Доминанте, тем самым выражая своё согласие исполнять их функции ( Тоника в данном случае – главная, а речь – о родственниках): удерживать поближе к Тонике (Субдоминанта) или осуществлять порыв к новизне, к выходу за пределы (Доминанта).

Субдоминантовую функцию исполняет, во-первых, сама же Субдоминанта (аккорд IV ступени). А к ней присоединяются и начинают исполнять её роль аккорды (а соответственно, и тональности) II и VI ступеней.

Например, в До-мажоре – это ре-минор и ля-минор.

На основании чего это они решили присоединиться именно к Субдоминанте?

А по закону тяготения, притяжения, гравитации. Их притягивают друг к другу общие звуки:

Рис. автора.

Видишь, у Субдоминанты довольно прочные связи с Тоникой. Именно Тоника тонического трезвучия их взаимно притягивает.

У Доминанты тоже есть связь с тоническим трезвучием, но… с его квинтой.

А квинта, мы знаем, всегда может увлечь в дальний путь без пределов…

Доминант-септаккорд с его обращениями возвращает к Тонике. Однако Доминанта всегда остаётся неустойчивой.

Рис. автора.

Все подробности о правилах поведения «родственников» главной тональности, их взаимных связях при модуляциях ты можешь узнать из того же «Практического учебника гармонии». Эти правила строги, как законы физики и математики, но удивительным образом они способствуют рождению невероятного числа таких непохожих произведений!

К слову, мы ведь тоже неповторимы, несмотря на действие общих для нас законов физики и генетики…

Думаю, тебя несколько удивит необычное расположение аккордов в примерах из учебника. Звуки этих аккордов раскинулись по гигантским вертикалям, на всё пространство обоих ключей.

Рис. автора.

Зачем так?

…Оргáнный масштаб: тысячеголосый хор флейт, – п р о с т р а н с т в о,

много пространства для дыхания тысяч труб, для свободного полёта звуков с их обертонами. Каждому звуку аккорда есть место развернуть с в о ю мелодию, и эти мелодии, встречаясь, связываясь друг с другом, сольются в новые аккорды… Полифония – многозвучие, многоголосие. Римский-Корсаков звукам аккордов даёт имена человеческих голосов. Снизу вверх (по правилам поведения звука): бас, тенор, альт, сопрано.

Когда мы поём, мы выдыхаем воздух-пространство; когда поёт оргáн, его трубы тоже выдыхают воздух-пространство.

Трудно на первый взгляд распознать порядок в этих разбросанных звуках, и тем удивительнее его обнаруживать – обнаруживать связанность звуков. Так удивительно, наверное, открывать связанность звёзд в космических безднах силами гравитации, общей сетью… Когда попривыкнешь ориентироваться, даже захватывает дух от открывающихся возможностей.

А сами ключи? Это же всё происходит в их владениях – всё это связанное непрерывное круженье-звучание. Как бы они удерживали всё это в своей власти, не будучи сами связанными?

Давай экспериментировать! Думать и экспериментировать.

Вернёмся к геометрии в пространстве. Вспомним, что басовый ключ у нас – левый узел (вяжется справа налево, по движению линии ключа), а скрипичный ключ – правый узел (получился в результате эксперимента).

Левый узел – ключ «ФА» – показывает квинту влево (на клавиатуре); правый узел – ключ «СОЛЬ» – показывает квинту вправо (тоже на клавиатуре). Место их встречи, или их общее начало, – ДО.

Мы можем представить себе отношения «ФА» и «СОЛЬ» в системе координат:

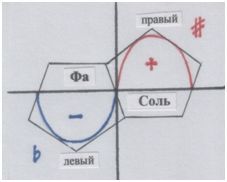
Рис. автора.

Конечно, мы подразумеваем, что где-то между ними «нулевая точка отсчёта» ДО. Но ведь в музыкальной системе, которая измеряет пространство-время не точками, а квинтами (самых разных масштабов), ДО измеряется тою же мерой. ДО – квинта вверх по отношению к ФА и квинта вниз по отношению к СОЛЬ. Относительность в действии! У ДО двойная роль: + и –, бемоль-диез в наложении друг на друга. В результате – нейтралитет. Вот смысл её «нуля». Если промоделировать это квинтами-узлами, они неизбежно выведут нас из прямоугольной системы координат, существующей на плоскости, в пространство. Вот как узлы покажут смысл ДО:

Модель автора.

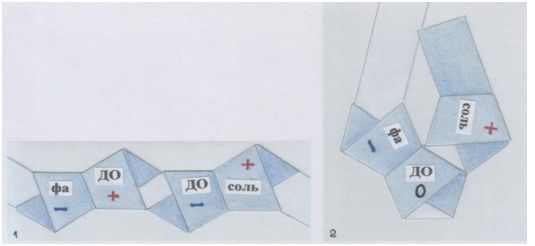
Рис. автора.

Остаётся довершить это стремление к соединению:

Рис. автора.

Оказавшись на свободе в пространстве, эта фигура продемонстрирует свойства ленты Мёбиуса: закольцованная бесконечность, в которой два сливаются в одно – две поверхности становятся одной, и, двигаясь в одном направлении, подобно звуку и Времени, мы охватываем две противоположности – низ и верх (глубину и высоту, «что было» и «что будет»).

К этому волшебству ты можешь прикоснуться, сделав эту простенькую модель.

Это волшебство двух ключей.

Какая же «печать» в нотной записи запечатлевает его?

О, она тебе так хорошо знакома, что ты, наверняка, даже не замечаешь её, когда открываешь ноты.

Акколада

– от франц.

accolade

– «

объятие

».

Тактовая черта, «пульсируя» на протяжении всего музыкального произведения, беспрестанно напоминает нам об акколаде-объятии.

А вот ключи и акколада в виде непрерывности, связанности:

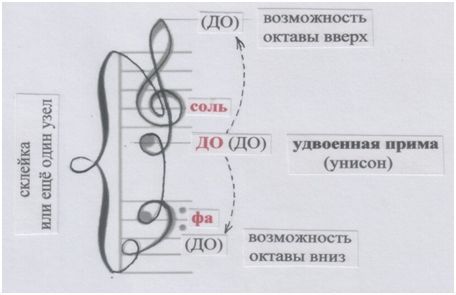
Рисунок и пометки автора.

Небо, открывающее нас.(На границе, где встречаются объективная реальность и сознание. Музыка и квантовая теория. Музыкальная модель мироздания на новом витке.)

Где живёт музыка?

…В небе.

Где живём мы?

…В небе.

?!

Ну с музыкой понятно: воздушные потоки (волны, вихри), которые обретают звучание внутри нас.

А мы?

…А где начинается небо? – У самой земли. И даже уходит в глубину, взрыхляя землю молекулами воздушными (углекислый газ, кислород, азот).

Это наше родное земное небо. В нём и электричество гроз, и магнитные потоки, «сшивающие» гигантскими петлями Землю с космосом, и звёздные фотоны (свет). Оно связывает Землю со Вселенной и размыкает «диапазон жизни» (атмосфера) на Земле.

Наверное, это самое удивительное и самое уникальное небо из всех небес Вселенной. Возможно, что другого такого больше нигде не существует, – как не существует и никогда не будет существовать точных копий каждого из нас (клоны не жизнеспособны).

Мы только опираемся на землю, но каждое утро поднимаемся вертикалью своей в небо, движемся в его пространстве и заполняем его пространством себя, когда дышим, когда впускаем свет в свои глаза и пульсирующий воздух в свои уши.

Небо открывает нас к жизни своими таинственными прозрачными ключами.

Самое удивительное в том, что они, эти ключи, так подходят к нам!

Возможно, что секрет этих ключей – в так уже хорошо знакомых нам квинтах-доминантах, организующих мир нашей жизни по подобиям – бесчисленным подобиям в самых разных масштабах и образах.

Музыка, её строй, явленный когда-то из догадок-интуиций (а потом и расчётов) первыми учёными-астрономами – строй, дарованный космическими небесами… Сколько ещё открытий он может подарить нам?

Ну пусть наши открытия не великие научные в строгом смысле.

В конце концов, у нас – игра. И мы моделируем наши открытия, играя бумажными полосками и … умозрением.

Небо открывает нас, чтобы мы открывали мир!

Давай-ка вернёмся к Квинтовому кругу тональностей. Подозреваю, что ещё не все его секреты нами разгаданы.

Пусть тональности этого Круга следуют по квинтам-узлам (из бумажной ленты). Вправо от ДО – правые узлы, диезные тональности; влево – левые узлы, бемольные тональности. ДО при этом сохраняет нейтралитет – то есть является удвоенным узлом, лево-правым. Так в унисоне ДО таятся две возможности проявить себя «втóрой» – октавным звуком.

Одна поверхность ленты у нас будет золотисто-жёлтой – мажорной; другая, параллельная (толщина листа создаёт параллель: верхняя поверхность – нижняя поверхность), – будет голубой, минорной.

В соответствии с Квинтовым к р у г о м мы будем вязать узлы по к р у г у. Если мы начнём с диезных тональностей, мы будем вязать только правые узлы.

Начнём!

…И что обнаружится?

За мажорным узлом неизбежно является минорный! Вот она, неизбежность параллельных миноров.

Следующая квинта-узел (следующая тональность) – опять мажор. Затем опять параллельный минор… Чередование!

Вспомним родственные тональности: родственники мажорных субдоминант и доминант – миноры, а минорных – мажоры. Тоже чередование. Как в звукоряде на нотном стане, в нотной геометрии – чередование звуков на линейках и между линейками. Свойства вращательной симметрии пространства. Она связана с чередованием.

Вяжем дальше. Мажоры-миноры, мажоры-миноры…

Интересно это место тем, что здесь очень явно даёт о себе знать энгармонизм – наличие диезных и бемольных способностей, таящихся в каждой тональности. То есть в этом месте появляется демонстрация того же нейтралитета, который присущ ДО. Да и располагается это место как раз напротив ДО, по отвесу.

Здесь мы можем поступить так. Либо от ДО вязать бемольные левые узлы до встречи в этом месте явного энгармонизма. Либо от этого места продолжить путь к ДО, поменяв «плюс» на «минус» – то есть правые диезные узлы на левые бемольные.

У меня получилась довольно любопытная модель музыкального строя.

Ты, конечно же, можешь сделать такую самостоятельно. Этот процесс создания модели даёт возможность о щ у т и т ь процесс сотворения музыкального строя, который сам по себе н е о щ у т и м.

В сложенном виде модель выглядит так:

Модели автора.

На что это похоже? Чему подобна эта фигура?

Сразу как-то вспоминается тот символ бесконечности (восьмёрка ∞), который получился в результате опыта, поясняющего истинную вращательную симметрию пространства.

Ещё это похоже на развёртку додекаэдра на плоскости:

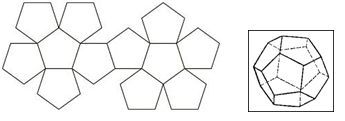
Рис. автора.

Только две противолежащие грани в таком додекаэдре оказались бы сквозными («невещественными»), да к тому же правым-левым узлом…

Сочетание правых-левых узлов (двойные узлы) в месте нейтрального ДО и в месте энгармонизмов в нашей модели спирали из узлов-квинт (тональностей) замыкают в кольцо. Причудливое кольцо. Из спиралей. Что же оно напоминает?

Подвесь-ка нашу модель на пальце в месте нейтрального ДО.

Какую фигуру мы увидим?

А очень даже знакомую фигуру.

(Но вначале посмотри на модели страничкой ниже.)

Это – уже представленная тебе модель в подвешенном состоянии:

Модели автора.

А ниже – знакомая модель музыкального строя в виде свёртывающейся винтом ленты правых и левых узлов, т.е. диезных и бемольных тональностей. Линия диезных тональностей показана красной нитью (соединяющей красные вершины узлов диезных тональностей), линия бемольных тональностей показана синей нитью (соединяющей синие вершины узлов бемольных тональностей).

Модели автора.