The Canterbury Puzzles, and Other Curious Problems

This little jest on the part of Major Trenchard is another trick puzzle, and the face of the roguish boy on the extreme right, with the figure 9 on his back, showed clearly that he was in the secret, whatever that secret might be. I have no doubt (bearing in mind the Major's hint as to the numbers being "properly regarded") that his answer was that depicted in the illustration, where boy No. 9 stands on his head and so converts his number into 6. This makes the total 36—an even number—and by making boys 3 and 4 change places with 7 and 8, we get 1278 and 5346, the figures of which, in each case, add up to 18. There are just three other ways in which the boys may be grouped: 1368—2457, 1467—2358, and 2367—1458.

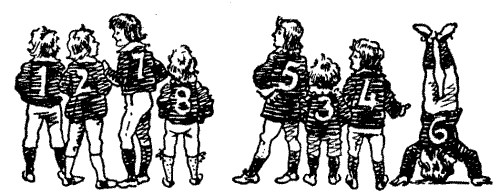
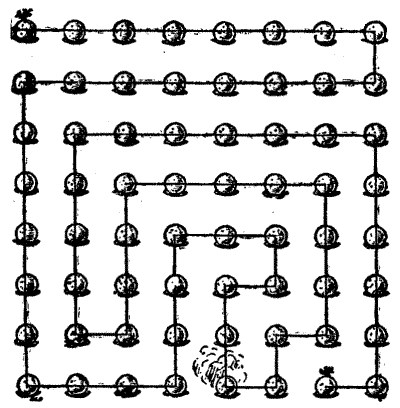
59.—Tasting the Plum Puddings

The diagram will show how this puzzle is to be solved. It is the only way within the conditions laid down. Starting at the pudding with holly at the top left-hand corner, we strike out all the puddings in twenty-one straight strokes, taste the steaming hot pudding at the end of the tenth stroke, and end at the second sprig of holly.

Here we have an example of a chess rook's path that is not re-entrant, but between two squares that are at the greatest possible distance from one another. For if it were desired to move, under the condition of visiting every square once and once only, from one corner square to the other corner square on the same diagonal, the feat is impossible.

There are a good many different routes for passing from one sprig of holly to the other in the smallest possible number of moves—twenty-one—but I have not counted them. I have recorded fourteen of these, and possibly there are more. Any one of these would serve our purpose, except for the condition that the tenth stroke shall end at the steaming hot pudding. This was introduced to stop a plurality of solutions—called by the maker of chess problems "cooks." I am not aware of more than one solution to this puzzle; but as I may not have recorded all the tours, I cannot make a positive statement on the point at the time of writing.

60.—Under the Mistletoe Bough

Everybody was found to have kissed everybody else once under the mistletoe, with the following additions and exceptions: No male kissed a male; no man kissed a married woman except his own wife; all the bachelors and boys kissed all the maidens and girls twice; the widower did not kiss anybody, and the widows did not kiss each other. Every kiss was returned, and the double performance was to count as one kiss. In making a list of the company, we can leave out the widower altogether, because he took no part in the osculatory exercise.

Now, if every one of these 39 persons kissed everybody else once, the number of kisses would be 741; and if the 12 bachelors and boys each kissed the 10 maidens and girls once again, we must add 120, making a total of 861 kisses. But as no married man kissed a married woman other than his own wife, we must deduct 42 kisses; as no male kissed another male, we must deduct 171 kisses; and as no widow kissed another widow, we must deduct 3 kisses. We have, therefore, to deduct 42+171+3=216 kisses from the above total of 861, and the result, 645, represents exactly the number of kisses that were actually given under the mistletoe bough.

61.—The Silver Cubes

There is no limit to the number of different dimensions that will give two cubes whose sum shall be exactly seventeen cubic inches. Here is the answer in the smallest possible numbers. One of the silver cubes must measure 2-23278/40831 inches along each edge, and the other must measure 11663/40831 inch. If the reader likes to undertake the task of cubing each number (that is, multiply each number twice by itself), he will find that when added together the contents exactly equal seventeen cubic inches. See also No. 20, "The Puzzle of the Doctor of Physic."

THE ADVENTURES OF THE PUZZLE CLUB

62.—The Ambiguous Photograph

One by one the members of the Club succeeded in discovering the key to the mystery of the Ambiguous Photograph, except Churton, who was at length persuaded to "give it up." Herbert Baynes then pointed out to him that the coat that Lord Marksford was carrying over his arm was a lady's coat, because the buttons are on the left side, whereas a man's coat always has the buttons on the right-hand side. Lord Marksford would not be likely to walk about the streets of Paris with a lady's coat over his arm unless he was accompanying the owner. He was therefore walking with the lady.

As they were talking a waiter brought a telegram to Baynes.

"Here you are," he said, after reading the message. "A wire from Dovey: 'Don't bother about photo. Find lady was the gentleman's sister, passing through Paris.' That settles it. You might notice that the lady was lightly clad, and therefore the coat might well be hers. But it is clear that the rain was only a sudden shower, and no doubt they were close to their destination, and she did not think it worth while to put the coat on."

63.—The Cornish Cliff Mystery

Melville's explanation of the Cornish Cliff Mystery was very simple when he gave it. Yet it was an ingenious trick that the two criminals adopted, and it would have completely succeeded had not our friends from the Puzzle Club accidentally appeared on the scene. This is what happened: When Lamson and Marsh reached the stile, Marsh alone walked to the top of the cliff, with Lamson's larger boots in his hands. Arrived at the edge of the cliff, he changed the boots and walked backwards to the stile, carrying his own boots.

This little manœuvre accounts for the smaller footprints showing a deeper impression at the heel, and the larger prints a deeper impression at the toe; for a man will walk more heavily on his heels when going forward, but will make a deeper impression with the toes in walking backwards. It will also account for the fact that the large footprints were sometimes impressed over the smaller ones, but never the reverse; also for the circumstance that the larger footprints showed a shorter stride, for a man will necessarily take a smaller stride when walking backwards. The pocket-book was intentionally dropped, to lead the police to discover the footprints, and so be put on the wrong scent.

64.—The Runaway Motor-Car

Russell found that there are just twelve five-figure numbers that have the peculiarity that the first two figures multiplied by the last three—all the figures being different, and there being no 0—will produce a number with exactly the same five figures, in a different order. But only one of these twelve begins with a 1—namely, 14926. Now, if we multiply 14 by 926, the result is 12964, which contains the same five figures. The number of the motor-car was therefore 14926.

Here are the other eleven numbers:—24651, 42678, 51246, 57834, 75231, 78624, 87435, 72936, 65281, 65983, and 86251.

Compare with the problems in "Digital Puzzles," section of A. in M., and with Nos. 93 and 101 in these pages.

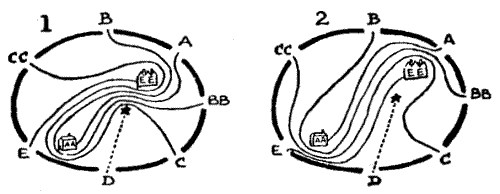
65.—The Mystery of Ravensdene Park

The diagrams show that there are two different ways in which the routes of the various persons involved in the Ravensdene Mystery may be traced, without any path ever crossing another. It depends whether the butler, E, went to the north or the south of the gamekeeper's cottage, and the gamekeeper, A, went to the south or the north of the hall. But it will be found that the only persons who could have approached Mr. Cyril Hastings without crossing a path were the butler, E, and the man, C. It was, however, a fact that the butler retired to bed five minutes before midnight, whereas Mr. Hastings did not leave his friend's house until midnight. Therefore the criminal must have been the man who entered the park at C.

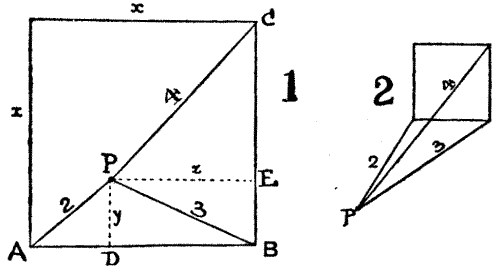
66.—The Buried Treasure

The field must have contained between 179 and 180 acres—to be more exact, 179.37254 acres. Had the measurements been 3, 2, and 4 furlongs respectively from successive corners, then the field would have been 209.70537 acres in area.

One method of solving this problem is as follows. Find the area of triangle APB in terms of x, the side of the square. Double the result=xy. Divide by x and then square, and we have the value of y2 in terms of x. Similarly find value of z2 in terms of x; then solve the equation y2+z2=32, which will come out in the form x4-20x2=-37. Therefore x2=10+(sqrt{63})=17.937254 square furlongs, very nearly, and as there are ten acres in one square furlong, this equals 179.37254 acres. If we take the negative root of the equation, we get the area of the field as 20.62746 acres, in which case the treasure would have been buried outside the field, as in Diagram 2. But this solution is excluded by the condition that the treasure was buried in the field. The words were, "The document … states clearly that the field is square, and that the treasure is buried in it."

THE PROFESSOR'S PUZZLES

67.—The Coinage Puzzle

The point of this puzzle turns on the fact that if the magic square were to be composed of whole numbers adding up 15 in all ways, the two must be placed in one of the corners. Otherwise fractions must be used, and these are supplied in the puzzle by the employment of sixpences and half-crowns. I give the arrangement requiring the fewest possible current English coins—fifteen. It will be seen that the amount in each corner is a fractional one, the sum required in the total being a whole number of shillings.

68.—The Postage Stamps Puzzles

The first of these puzzles is based on a similar principle, though it is really much easier, because the condition that nine of the stamps must be of different values makes their selection a simple matter, though how they are to be placed requires a little thought or trial until one knows the rule respecting putting the fractions in the corners. I give the solution.

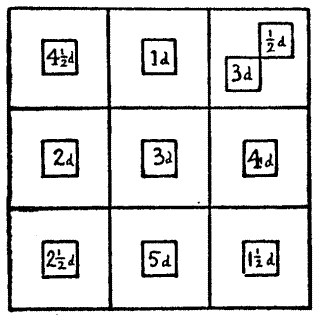
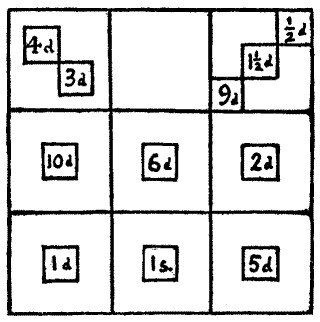
I also show the solution to the second stamp puzzle. All the columns, rows, and diagonals add up 1s. 6d. There is no stamp on one square, and the conditions did not forbid this omission. The stamps at present in circulation are these:—½d., 1d., 1-½d., 2d., 2-½d., 3d., 4d., 5d., 6d., 9d., 10d., 1s., 2s. 6d., 5s., 10s., £1, and £5. In the first solution the numbers are in arithmetical progression—1, 1-½, 2, 2-½, 3, 3-½, 4, 4-½, 5. But any nine numbers will form a magic square if we can write them thus:—

where the horizontal differences are all alike and the vertical differences all alike, but not necessarily the same as the horizontal. This happens in the case of the second solution, the numbers of which may be written:—

Also in the case of the solution to No. 67, the Coinage Puzzle, the numbers are, in shillings:—

If there are to be nine different numbers, 0 may occur once (as in the solution to No. 22). Yet one might construct squares with negative numbers, as follows:—

69.—The Frogs and Tumblers

It is perfectly true, as the Professor said, that there is only one solution (not counting a reversal) to this puzzle. The frogs that jump are George in the third horizontal row; Chang, the artful-looking batrachian at the end of the fourth row; and Wilhelmina, the fair creature in the seventh row. George jumps downwards to the second tumbler in the seventh row; Chang, who can only leap short distances in consequence of chronic rheumatism, removes somewhat unwillingly to the glass just above him—the eighth in the third row; while Wilhelmina, with all the sprightliness of her youth and sex, performs the very creditable saltatory feat of leaping to the fourth tumbler in the fourth row. In their new positions, as shown in the accompanying diagram, it will be found that of the eight frogs no two are in line vertically, horizontally, or diagonally.

70.—Romeo and Juliet

This is rather a difficult puzzle, though, as the Professor remarked when Hawkhurst hit on the solution, it is "just one of those puzzles that a person might solve at a glance" by pure luck. Yet when the solution, with its pretty, symmetrical arrangement, is seen, it looks ridiculously simple.

It will be found that Romeo reaches Juliet's balcony after visiting every house once and only once, and making fourteen turnings, not counting the turn he makes at starting. These are the fewest turnings possible, and the problem can only be solved by the route shown or its reversal.

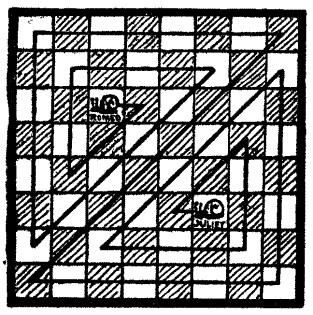
71.—Romeo's Second Journey

In order to take his trip through all the white squares only with the fewest possible turnings, Romeo would do well to adopt the route I have shown, by means of which only sixteen turnings are required to perform the feat. The Professor informs me that the Helix Aspersa, or common or garden snail, has a peculiar aversion to making turnings—so much so that one specimen with which he made experiments went off in a straight line one night and has never come back since.

72.—The Frogs who would a-wooing go

This is one of those puzzles in which a plurality of solutions is practically unavoidable. There are two or three positions into which four frogs may jump so as to form five rows with four in each row, but the case I have given is the most satisfactory arrangement.

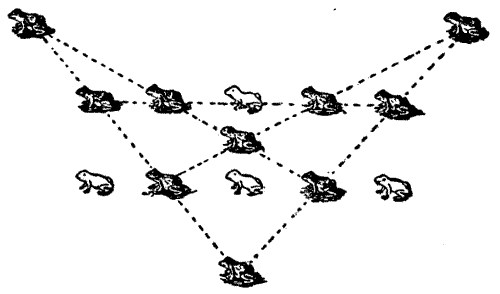
The frogs that have jumped have left their astral bodies behind, in order to show the reader the positions which they originally occupied. Chang, the frog in the middle of the upper row, suffering from rheumatism, as explained above in the Frogs and Tumblers solution, makes the shortest jump of all—a little distance between the two rows; George and Wilhelmina leap from the ends of the lower row to some distance N. by N.W. and N. by N.E. respectively; while the frog in the middle of the lower row, whose name the Professor forgot to state, goes direct S.

73.—The Game of Kayles

To win at this game you must, sooner or later, leave your opponent an even number of similar groups. Then whatever he does in one group you repeat in a similar group. Suppose, for example, that you leave him these groups: o.o.ooo.ooo. Now, if he knocks down a single, you knock down a single; if he knocks down two in one triplet, you knock down two in the other triplet; if he knocks down the central kayle in a triplet, you knock down the central one in the other triplet. In this way you must eventually win. As the game is started with the arrangement o.ooooooooooo, the first player can always win, but only by knocking down the sixth or tenth kayle (counting the one already fallen as the second), and this leaves in either case o.ooo.ooooooo, as the order of the groups is of no importance. Whatever the second player now does, this can always be resolved into an even number of equal groups. Let us suppose that he knocks down the single one; then we play to leave him oo.ooooooo. Now, whatever he does we can afterwards leave him either ooo.ooo or o.oo.ooo. We know why the former wins, and the latter wins also; because, however he may play, we can always leave him either o.o, or o.o.o.o, or oo.oo, as the case may be. The complete analysis I can now leave for the amusement of the reader.

74.—The Broken Chessboard

The illustration will show how the thirteen pieces can be put together so as to construct the perfect board, and the reverse problem of cutting these particular pieces out will be found equally entertaining.

Compare with Nos. 293 and 294 in A. in M.

75.—The Spider and the Fly

Though this problem was much discussed in the Daily Mail from 18th January to 7th February 1905, when it appeared to create great public interest, it was actually first propounded by me in the Weekly Dispatch of 14th June 1903.

Imagine the room to be a cardboard box. Then the box may be cut in various different ways, so that the cardboard may be laid flat on the table. I show four of these ways, and indicate in every case the relative positions of the spider and the fly, and the straightened course which the spider must take without going off the cardboard. These are the four most favourable cases, and it will be found that the shortest route is in No. 4, for it is only 40 feet in length (add the square of 32 to the square of 24 and extract the square root). It will be seen that the spider actually passes along five of the six sides of the room! Having marked the route, fold the box up (removing the side the spider does not use), and the appearance of the shortest course is rather surprising. If the spider had taken what most persons will consider obviously the shortest route (that shown in No. 1), he would have gone 42 feet! Route No. 2 is 43.174 feet in length, and Route No. 3 is 40.718 feet.

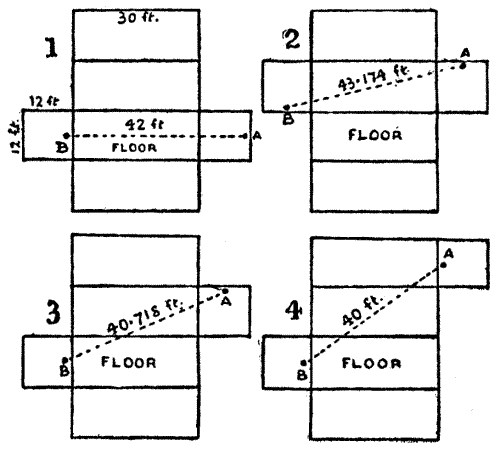
I will leave the reader to discover which are the shortest routes when the spider and the fly are 2, 3, 4, 5, and 6 feet from the ceiling and the floor respectively.

76.—The Perplexed Cellarman

Brother John gave the first man three large bottles and one small bottleful of wine, and one large and three small empty bottles. To each of the other two men he gave two large and three small bottles of wine, and two large and one small empty bottle. Each of the three then receives the same quantity of wine, and the same number of each size of bottle.

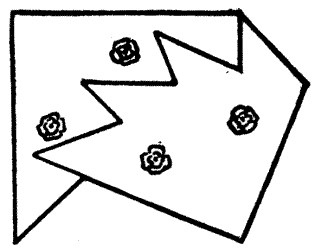
77.—Making a Flag

The diagram shows how the piece of bunting is to be cut into two pieces. Lower the piece on the right one "tooth," and they will form a perfect square, with the roses symmetrically placed.

It will be found interesting to compare this with No. 154 in A. in M.

78.—Catching the Hogs

A very short examination of this puzzle game should convince the reader that Hendrick can never catch the black hog, and that the white hog can never be caught by Katrün.

Each hog merely runs in and out of one of the nearest corners and can never be captured. The fact is, curious as it must at first sight appear, a Dutchman cannot catch a black hog, and a Dutchwoman can never capture a white one! But each can, without difficulty, catch one of the other colour.

So if the first player just determines that he will send Hendrick after the white porker and Katrün after the black one, he will have no difficulty whatever in securing both in a very few moves.

It is, in fact, so easy that there is no necessity whatever to give the line of play. We thus, by means of the game, solve the puzzle in real life, why the Dutchman and his wife could not catch their pigs: in their simplicity and ignorance of the peculiarities of Dutch hogs, each went after the wrong animal.

The little principle involved in this puzzle is that known to chess-players as "getting the opposition." The rule, in the case of my puzzle (where the moves resemble rook moves in chess, with the added condition that the rook may only move to an adjoining square), is simply this. Where the number of squares on the same row, between the man or woman and the hog, is odd, the hog can never be captured; where the number of squares is even, a capture is possible. The number of squares between Hendrick and the black hog, and between Katrün and the white hog, is 1 (an odd number), therefore these individuals cannot catch the animals they are facing. But the number between Hendrick and the white hog, and between Katrün and the black one, is 6 (an even number), therefore they may easily capture those behind them.

79.—The Thirty-one Game

By leading with a 5 the first player can always win. If your opponent plays another 5, you play a 2 and score 12. Then as often as he plays a 5 you play a 2, and if at any stage he drops out of the series, 3, 10, 17, 24, 31, you step in and win. If after your lead of 5 he plays anything but another 5, you make 10 or 17 and win. The first player may also win by leading a 1 or a 2, but the play is complicated. It is, however, well worth the reader's study.

80.—The Chinese Railways

This puzzle was artfully devised by the yellow man. It is not a matter for wonder that the representatives of the five countries interested were bewildered. It would have puzzled the engineers a good deal to construct those circuitous routes so that the various trains might run with safety. Diagram 1 shows directions for the five systems of lines, so that no line shall ever cross another, and this appears to be the method that would require the shortest possible mileage.

The reader may wish to know how many different solutions there are to the puzzle. To this I should answer that the number is indeterminate, and I will explain why. If we simply consider the case of line A alone, then one route would be Diagram 2, another 3, another 4, and another 5. If 3 is different from 2, as it undoubtedly is, then we must regard 5 as different from 4. But a glance at the four diagrams, 2, 3, 4, 5, in succession will show that we may continue this "winding up" process for ever; and as there will always be an unobstructed way (however long and circuitous) from stations B and E to their respective main lines, it is evident that the number of routes for line A alone is infinite. Therefore the number of complete solutions must also be infinite, if railway lines, like other lines, have no breadth; and indeterminate, unless we are told the greatest number of parallel lines that it is possible to construct in certain places. If some clear condition, restricting these "windings up," were given, there would be no great difficulty in giving the number of solutions. With any reasonable limitation of the kind, the number would, I calculate, be little short of two thousand, surprising though it may appear.