The Canterbury Puzzles, and Other Curious Problems

15.—The Cook's Puzzle

There were four portions of warden pie and four portions of venison pasty to be distributed among eight out of eleven guests. But five out of the eleven will only eat the pie, four will only eat the pasty, and two are willing to eat of either. Any possible combination must fall into one of the following groups. (i.) Where the warden pie is distributed entirely among the five first mentioned; (ii.) where only one of the accommodating pair is given pie; (iii.) where the other of the pair is given pie; (iv.) where both of the pair are given pie. The numbers of combinations are: (i.) = 75, (ii.) = 50, (iii.) = 10, (iv.) = 10—making in all 145 ways of selecting the eight participants. A great many people will give the answer as 185, by overlooking the fact that in forty cases in class (iii.) precisely the same eight guests would be sharing the meal as in class (ii.), though the accommodating pair would be eating differently of the two dishes. This is the point that upset the calculations of the company.

16.—The Sompnour's Puzzle

The number that the Sompnour confided to the Wife of Bath was twenty-nine, and she was told to begin her count at the Doctor of Physic, who will be seen in the illustration standing the second on her right. The first count of twenty-nine falls on the Shipman, who steps out of the ring. The second count falls on the Doctor, who next steps out. The remaining three counts fall respectively on the Cook, the Sompnour, and the Miller. The ladies would, therefore, have been left in possession had it not been for the unfortunate error of the good Wife. Any multiple of 2,520 added to 29 would also have served the same purpose, beginning the count at the Doctor.

17.—The Monk's Puzzle

The Monk might have placed dogs in the kennels in two thousand nine hundred and twenty-six different ways, so that there should be ten dogs on every side. The number of dogs might vary from twenty to forty, and as long as the Monk kept his animals within these limits the thing was always possible.

The general solution to this puzzle is difficult. I find that for n dogs on every side of the square, the number of different ways is (n4 + 10n3 + 38n2 + 62n + 33) / 48, where n is odd, and ((n4 + 10n3 + 38n2 + 68n) / 48) + 1, where n is even, if we count only those arrangements that are fundamentally different. But if we count all reversals and reflections as different, as the Monk himself did, then n dogs (odd or even) may be placed in ((n4 + 6n3 + 14n2 + 15n) / 6) + 1 ways. In order that there may be n dogs on every side, the number must not be less than 2n nor greater than 4n, but it may be any number within these limits.

An extension of the principle involved in this puzzle is given in No. 42, "The Riddle of the Pilgrims." See also "The Eight Villas" and "A Dormitory Puzzle" in A. in M.

18.—The Shipman's Puzzle

There are just two hundred and sixty-four different ways in which the ship Magdalen might have made her ten annual voyages without ever going over the same course twice in a year. Every year she must necessarily end her tenth voyage at the island from which she first set out.

19.—The Puzzle of the Prioress

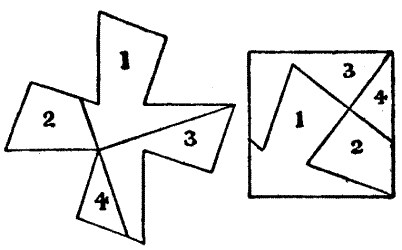
The Abbot of Chertsey was quite correct. The curiously-shaped cross may be cut into four pieces that will fit together and form a perfect square. How this is done is shown in the illustration.

See also p. 31 in A. in M.

20.—The Puzzle of the Doctor of Physic

Here we have indeed a knotty problem. Our text-books tell us that all spheres are similar, and that similar solids are as the cubes of corresponding lengths. Therefore, as the circumferences of the two phials were one foot and two feet respectively and the cubes of one and two added together make nine, what we have to find is two other numbers whose cubes added together make nine. These numbers clearly must be fractional. Now, this little question has really engaged the attention of learned men for two hundred and fifty years; but although Peter de Fermat showed in the seventeenth century how an answer may be found in two fractions with a denominator of no fewer than twenty-one figures, not only are all the published answers, by his method, that I have seen inaccurate, but nobody has ever published the much smaller result that I now print. The cubes of (415280564497 / 348671682660) and (676702467503 / 348671682660) added together make exactly nine, and therefore these fractions of a foot are the measurements of the circumferences of the two phials that the Doctor required to contain the same quantity of liquid as those produced. An eminent actuary and another correspondent have taken the trouble to cube out these numbers, and they both find my result quite correct.

If the phials were one foot and three feet in circumference respectively, then an answer would be that the cubes of (63284705 / 21446828) and (28340511 / 21446828) added together make exactly 28. See also No. 61, "The Silver Cubes."

Given a known case for the expression of a number as the sum or difference of two cubes, we can, by formula, derive from it an infinite number of other cases alternately positive and negative. Thus Fermat, starting from the known case 13 + 23 = 9 (which we will call a fundamental case), first obtained a negative solution in bigger figures, and from this his positive solution in bigger figures still. But there is an infinite number of fundamentals, and I found by trial a negative fundamental solution in smaller figures than his derived negative solution, from which I obtained the result shown above. That is the simple explanation.

We can say of any number up to 100 whether it is possible or not to express it as the sum of two cubes, except 66. Students should read the Introduction to Lucas's Théorie des Nombres, p. xxx.

Some years ago I published a solution for the case of

of which Legendre gave at some length a "proof" of impossibility; but I have since found that Lucas anticipated me in a communication to Sylvester.

21.—The Ploughman's Puzzle

The illustration shows how the sixteen trees might have been planted so as to form as many as fifteen straight rows with four trees in every row. This is in excess of what was for a long time believed to be the maximum number of rows possible; and though with our present knowledge I cannot rigorously demonstrate that fifteen rows cannot be beaten, I have a strong "pious opinion" that it is the highest number of rows obtainable.

22.—The Franklin's Puzzle

The answer to this puzzle is shown in the illustration, where the numbers on the sixteen bottles all add up to 30 in the ten straight directions. The trick consists in the fact that, although the six bottles (3, 5, 6, 9, 10, and 15) in which the flowers have been placed are not removed, yet the sixteen need not occupy exactly the same position on the table as before. The square is, in fact, formed one step further to the left.

23.—The Squire's Puzzle

The portrait may be drawn in a single line because it contains only two points at which an odd number of lines meet, but it is absolutely necessary to begin at one of these points and end at the other. One point is near the outer extremity of the King's left eye; the other is below it on the left cheek.

24.—The Friar's Puzzle

The five hundred silver pennies might have been placed in the four bags, in accordance with the stated conditions, in exactly 894,348 different ways. If there had been a thousand coins there would be 7,049,112 ways. It is a difficult problem in the partition of numbers. I have a single formula for the solution of any number of coins in the case of four bags, but it was extremely hard to construct, and the best method is to find the twelve separate formulas for the different congruences to the modulus 12.

25.—The Parson's Puzzle

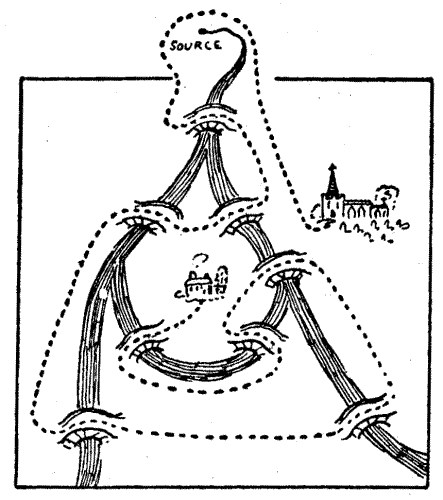
A very little examination of the original drawing will have shown the reader that, as he will have at first read the conditions, the puzzle is quite impossible of solution. We have therefore to look for some loophole in the actual conditions as they were worded. If the Parson could get round the source of the river, he could then cross every bridge once and once only on his way to church, as shown in the annexed illustration. That this was not prohibited we shall soon find. Though the plan showed all the bridges in his parish, it only showed "part of" the parish itself. It is not stated that the river did not take its rise in the parish, and since it leads to the only possible solution, we must assume that it did. The answer would be, therefore, as shown. It should be noted that we are clearly prevented from considering the possibility of getting round the mouth of the river, because we are told it "joined the sea some hundred miles to the south," while no parish ever extended a hundred miles!

26.—The Haberdasher's Puzzle

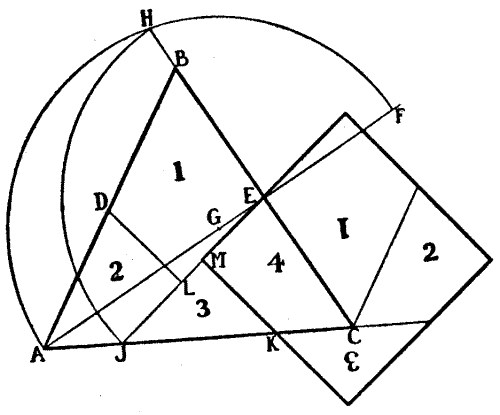
The illustration will show how the triangular piece of cloth may be cut into four pieces that will fit together and form a perfect square. Bisect AB in D and BC in E; produce the line AE to F making EF equal to EB; bisect AF in G and describe the arc AHF; produce EB to H, and EH is the length of the side of the required square; from E with distance EH, describe the arc HJ, and make JK equal to BE; now, from the points D and K drop perpendiculars on EJ at L and M. If you have done this accurately, you will now have the required directions for the cuts.

I exhibited this problem before the Royal Society, at Burlington House, on 17th May 1905, and also at the Royal Institution in the following month, in the more general form:—"A New Problem on Superposition: a demonstration that an equilateral triangle can be cut into four pieces that may be reassembled to form a square, with some examples of a general method for transforming all rectilinear triangles into squares by dissection." It was also issued as a challenge to the readers of the Daily Mail (see issues of 1st and 8th February 1905), but though many hundreds of attempts were sent in there was not a single solver. Credit, however, is due to Mr. C. W. M'Elroy, who alone sent me the correct solution when I first published the problem in the Weekly Dispatch in 1902.

I add an illustration showing the puzzle in a rather curious practical form, as it was made in polished mahogany with brass hinges for use by certain audiences. It will be seen that the four pieces form a sort of chain, and that when they are closed up in one direction they form the triangle, and when closed in the other direction they form the square.

27.—The Dyer's Puzzle

The correct answer is 18,816 different ways. The general formula for six fleurs-de-lys for all squares greater than 22 is simply this: Six times the square of the number of combinations of n things, taken three at a time, where n represents the number of fleurs-de-lys in the side of the square. Of course where n is even the remainders in rows and columns will be even, and where n is odd the remainders will be odd.

For further solution, see No. 358 in A. in M.

28.—The Great Dispute between the Friar and the Sompnour

In this little problem we attempted to show how, by sophistical reasoning, it may apparently be proved that the diagonal of a square is of precisely the same length as two of the sides. The puzzle was to discover the fallacy, because it is a very obvious fallacy if we admit that the shortest distance between two points is a straight line. But where does the error come in?

Well, it is perfectly true that so long as our zigzag path is formed of "steps" parallel to the sides of the square that path must be of the same length as the two sides. It does not matter if you have to use the most powerful microscope obtainable; the rule is always true if the path is made up of steps in that way. But the error lies in the assumption that such a zigzag path can ever become a straight line. You may go on increasing the number of steps infinitely—that is, there is no limit whatever theoretically to the number of steps that can be made—but you can never reach a straight line by such a method. In fact it is just as much a "jump" to a straight line if you have a billion steps as it is at the very outset to pass from the two sides to the diagonal. It would be just as absurd to say we might go on dropping marbles into a basket until they become sovereigns as to say we can increase the number of our steps until they become a straight line. There is the whole thing in a nutshell.

29.—Chaucer's Puzzle

The surface of water or other liquid is always spherical, and the greater any sphere is the less is its convexity. Hence the top diameter of any vessel at the summit of a mountain will form the base of the segment of a greater sphere than it would at the bottom. This sphere, being greater, must (from what has been already said) be less convex; or, in other words, the spherical surface of the water must be less above the brim of the vessel, and consequently it will hold less at the top of a mountain than at the bottom. The reader is therefore free to select any mountain he likes in Italy—or elsewhere!

30.—The Puzzle of the Canon's Yeoman

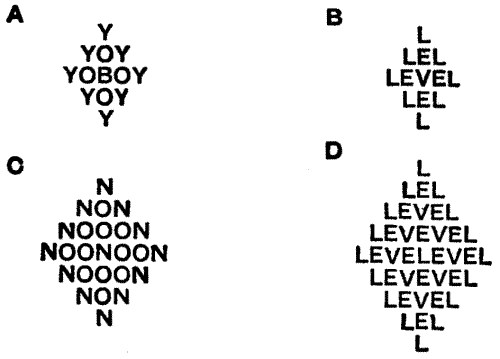
The number of different ways is 63,504. The general formula for such arrangements, when the number of letters in the sentence is 2n + 1, and it is a palindrome without diagonal readings, is [4(2n – 1)]2.

I think it will be well to give here a formula for the general solution of each of the four most common forms of the diamond-letter puzzle. By the word "line" I mean the complete diagonal. Thus in A, B, C, and D, the lines respectively contain 5, 5, 7, and 9 letters. A has a non-palindrome line (the word being BOY), and the general solution for such cases, where the line contains 2n + 1 letters, is 4(2n – 1). Where the line is a single palindrome, with its middle letter in the centre, as in B, the general formula is [4(2n – 1)]2. This is the form of the Rat-catcher's Puzzle, and therefore the expression that I have given above. In cases C and D we have double palindromes, but these two represent very different types. In C, where the line contains 4n-1 letters, the general expression is 4(22n-2). But D is by far the most difficult case of all.

I had better here state that in the diamonds under consideration (i.) no diagonal readings are allowed—these have to be dealt with specially in cases where they are possible and admitted; (ii.) readings may start anywhere; (iii.) readings may go backwards and forwards, using letters more than once in a single reading, but not the same letter twice in immediate succession. This last condition will be understood if the reader glances at C, where it is impossible to go forwards and backwards in a reading without repeating the first O touched—a proceeding which I have said is not allowed. In the case D it is very different, and this is what accounts for its greater difficulty. The formula for D is this:

where the number of letters in the line is 4n + 1. In the example given there are therefore 400 readings for n = 2.

See also Nos. 256, 257, and 258 in A. in M.

31.—The Manciple's Puzzle

The simple Ploughman, who was so ridiculed for his opinion, was perfectly correct: the Miller should receive seven pieces of money, and the Weaver only one. As all three ate equal shares of the bread, it should be evident that each ate 8/3 of a loaf. Therefore, as the Miller provided 15/3 and ate 8/3, he contributed 7/3 to the Manciple's meal; whereas the Weaver provided 9/3, ate 8/3, and contributed only 1/3. Therefore, since they contributed to the Manciple in the proportion of 7 to 1, they must divide the eight pieces of money in the same proportion.

PUZZLING TIMES AT SOLVAMHALL CASTLE

SIR HUGH EXPLAINS HIS PROBLEMS

The friends of Sir Hugh de Fortibus were so perplexed over many of his strange puzzles that at a gathering of his kinsmen and retainers he undertook to explain his posers.

"Of a truth," said he, "some of the riddles that I have put forth would greatly tax the wit of the unlettered knave to rede; yet will I try to show the manner thereof in such way that all may have understanding. For many there be who cannot of themselves do all these things, but will yet study them to their gain when they be given the answers, and will take pleasure therein."

32.—The Game of Bandy-Ball

Sir Hugh explained, in answer to this puzzle, that as the nine holes were 300, 250, 200, 325, 275, 350, 225, 375, and 400 yards apart, if a man could always strike the ball in a perfectly straight line and send it at will a distance of either 125 yards or 100 yards, he might go round the whole course in 26 strokes. This is clearly correct, for if we call the 125 stroke the "drive" and the 100 stroke the "approach," he could play as follows:—The first hole could be reached in 3 approaches, the second in 2 drives, the third in 2 approaches, the fourth in 2 approaches and 1 drive, the fifth in 3 drives and 1 backward approach, the sixth in 2 drives and 1 approach, the seventh in 1 drive and 1 approach, the eighth in 3 drives, and the ninth hole in 4 approaches. There are thus 26 strokes in all, and the feat cannot be performed in fewer.

33.—Tilting at the Ring

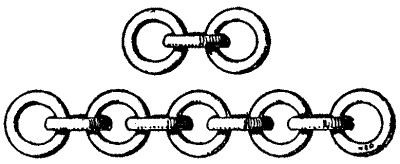
"By my halidame!" exclaimed Sir Hugh, "if some of yon varlets had been put in chains, which for their sins they do truly deserve, then would they well know, mayhap, that the length of any chain having like rings is equal to the inner width of a ring multiplied by the number of rings and added to twice the thickness of the iron whereof it is made. It may be shown that the inner width of the rings used in the tilting was one inch and two-thirds thereof, and the number of rings Stephen Malet did win was three, and those that fell to Henry de Gournay would be nine."

The knight was quite correct, for 1-2/3 in. × 3 + 1 in. = 6 in., and 1-2/3 in. x 9 + 1 in. = 16 in. Thus De Gournay beat Malet by six rings. The drawing showing the rings may assist the reader in verifying the answer and help him to see why the inner width of a link multiplied by the number of links and added to twice the thickness of the iron gives the exact length. It will be noticed that every link put on the chain loses a length equal to twice the thickness of the iron.

34.—The Noble Demoiselle

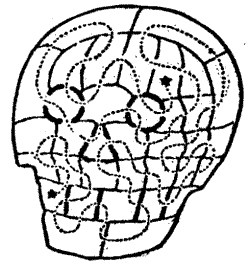
"Some here have asked me," continued Sir Hugh, "how they may find the cell in the Dungeon of the Death's-head wherein the noble maiden was cast. Beshrew me! but 'tis easy withal when you do but know how to do it. In attempting to pass through every door once, and never more, you must take heed that every cell hath two doors or four, which be even numbers, except two cells, which have but three. Now, certes, you cannot go in and out of any place, passing through all the doors once and no more, if the number of doors be an odd number. But as there be but two such odd cells, yet may we, by beginning at the one and ending at the other, so make our journey in many ways with success. I pray you, albeit, to mark that only one of these odd cells lieth on the outside of the dungeon, so we must perforce start therefrom. Marry, then, my masters, the noble demoiselle must needs have been wasting in the other."

The drawing will make this quite clear to the reader. The two "odd cells" are indicated by the stars, and one of the many routes that will solve the puzzle is shown by the dotted line. It is perfectly certain that you must start at the lower star and end at the upper one; therefore the cell with the star situated over the left eye must be the one sought.

35.—The Archery Butt

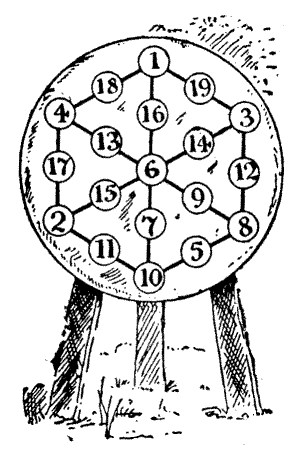
"It hath been said that the proof of a pudding is ever in the eating thereof, and by the teeth of Saint George I know no better way of showing how this placing of the figures may be done than by the doing of it. Therefore have I in suchwise written the numbers that they do add up to twenty and three in all the twelve lines of three that are upon the butt."

I think it well here to supplement the solution of De Fortibus with a few remarks of my own. The nineteen numbers may be so arranged that the lines will add up to any number we may choose to select from 22 to 38 inclusive, excepting 30. In some cases there are several different solutions, but in the case of 23 there are only two. I give one of these. To obtain the second solution exchange respectively 7, 10, 5, 8, 9, in the illustration, with 13, 4, 17, 2, 15. Also exchange 18 with 12, and the other numbers may remain unmoved. In every instance there must be an even number in the central place, and any such number from 2 to 18 may occur. Every solution has its complementary. Thus, if for every number in the accompanying drawing we substitute the difference between it and 20, we get the solution in the case of 37. Similarly, from the arrangement in the original drawing, we may at once obtain a solution for the case of 38.

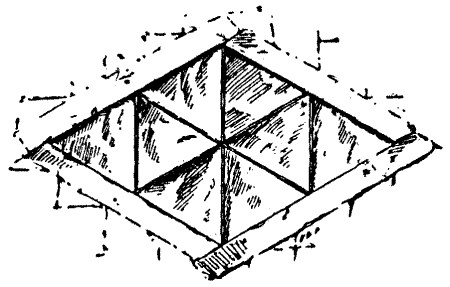
36.—The Donjon Keep Window

In this case Sir Hugh had greatly perplexed his chief builder by demanding that he should make a window measuring one foot on every side and divided by bars into eight lights, having all their sides equal. The illustration will show how this was to be done. It will be seen that if each side of the window measures one foot, then each of the eight triangular lights is six inches on every side.

"Of a truth, master builder," said De Fortibus slyly to the architect, "I did not tell thee that the window must be square, as it is most certain it never could be."

37.—The Crescent and the Cross

"By the toes of St. Moden," exclaimed Sir Hugh de Fortibus when this puzzle was brought up, "my poor wit hath never shaped a more cunning artifice or any more bewitching to look upon. It came to me as in a vision, and ofttimes have I marvelled at the thing, seeing its exceeding difficulty. My masters and kinsmen, it is done in this wise."