The Canterbury Puzzles, and Other Curious Problems

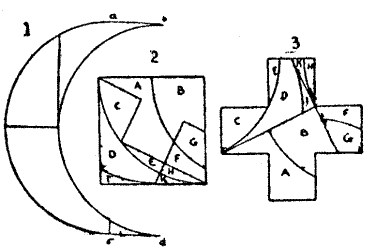
The worthy knight then pointed out that the crescent was of a particular and somewhat irregular form—the two distances a to b and c to d being straight lines, and the arcs ac and bd being precisely similar. He showed that if the cuts be made as in Figure 1, the four pieces will fit together and form a perfect square, as shown in Figure 2, if we there only regard the three curved lines. By now making the straight cuts also shown in Figure 2, we get the ten pieces that fit together, as in Figure 3, and form a perfectly symmetrical Greek cross. The proportions of the crescent and the cross in the original illustration were correct, and the solution can be demonstrated to be absolutely exact and not merely approximate.

I have a solution in considerably fewer pieces, but it is far more difficult to understand than the above method, in which the problem is simplified by introducing the intermediate square.

38.—The Amulet

The puzzle was to place your pencil on the A at the top of the amulet and count in how many different ways you could trace out the word "Abracadabra" downwards, always passing from a letter to an adjoining one.

"Now, mark ye, fine fellows," said Sir Hugh to some who had besought him to explain, "that at the very first start there be two ways open: whichever B ye select, there will be two several ways of proceeding (twice times two are four); whichever R ye select, there be two ways of going on (twice times four are eight); and so on until the end. Each letter in order from A downwards may so be reached in 2, 4, 8, 16, 32, etc., ways. Therefore, as there be ten lines or steps in all from A to the bottom, all ye need do is to multiply ten 2's together, and truly the result, 1024, is the answer thou dost seek."

39.—The Snail on the Flagstaff

Though there was no need to take down and measure the staff, it is undoubtedly necessary to find its height before the answer can be given. It was well known among the friends and retainers of Sir Hugh de Fortibus that he was exactly six feet in height. It will be seen in the original picture that Sir Hugh's height is just twice the length of his shadow. Therefore we all know that the flagstaff will, at the same place and time of day, be also just twice as long as its shadow. The shadow of the staff is the same length as Sir Hugh's height; therefore this shadow is six feet long, and the flagstaff must be twelve feet high. Now, the snail, by climbing up three feet in the daytime and slipping back two feet by night, really advances one foot in a day of twenty-four hours. At the end of nine days it is three feet from the top, so that it reaches its journey's end on the tenth day.

The reader will doubtless here exclaim, "This is all very well; but how were we to know the height of Sir Hugh? It was never stated how tall he was!" No, it was not stated in so many words, but it was none the less clearly indicated to the reader who is sharp in these matters. In the original illustration to the donjon keep window Sir Hugh is shown standing against a wall, the window in which is stated to be one foot square on the inside. Therefore, as his height will be found by measurement to be just six times the inside height of the window, he evidently stands just six feet in his boots!

40.—Lady Isabel's Casket

The last puzzle was undoubtedly a hard nut, but perhaps difficulty does not make a good puzzle any the less interesting when we are shown the solution. The accompanying diagram indicates exactly how the top of Lady Isabel de Fitzarnulph's casket was inlaid with square pieces of rare wood (no two squares alike) and the strip of gold 10 inches by a quarter of an inch. This is the only possible solution, and it is a singular fact (though I cannot here show the subtle method of working) that the number, sizes, and order of those squares are determined by the given dimensions of the strip of gold, and the casket can have no other dimensions than 20 inches square. The number in a square indicates the length in inches of the side of that square, so the accuracy of the answer can be checked almost at a glance.

Sir Hugh de Fortibus made some general concluding remarks on the occasion that are not altogether uninteresting to-day.

"Friends and retainers," he said, "if the strange offspring of my poor wit about which we have held pleasant counsel to-night hath mayhap had some small interest for ye, let these matters serve to call to mind the lesson that our fleeting life is rounded and beset with enigmas. Whence we came and whither we go be riddles, and albeit such as these we may never bring within our understanding, yet there be many others with which we and they that do come after us will ever strive for the answer. Whether success do attend or do not attend our labour, it is well that we make the attempt; for 'tis truly good and honourable to train the mind, and the wit, and the fancy of man, for out of such doth issue all manner of good in ways unforeseen for them that do come after us."

THE MERRY MONKS OF RIDDLEWELL

41.—The Riddle of the Fish-pond

Number the fish baskets in the illustration from 1 to 12 in the direction that Brother Jonathan is seen to be going. Starting from 1, proceed as follows, where "1 to 4" means, take the fish from basket No. 1 and transfer it to basket No. 4:—

1 to 4, 5 to 8, 9 to 12, 3 to 6, 7 to 10, 11 to 2, and complete the last revolution to 1, making three revolutions in all. Or you can proceed this way:—

4 to 7, 8 to 11, 12 to 3, 2 to 5, 6 to 9, 10 to 1.

It is easy to solve in four revolutions, but the solutions in three are more difficult to discover.

42.—The Riddle of the Pilgrims

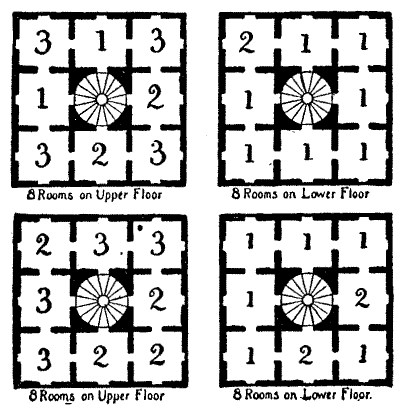
If it were not for the Abbot's conditions that the number of guests in any room may not exceed three, and that every room must be occupied, it would have been possible to accommodate either 24, 27, 30, 33, 36, 39, or 42 pilgrims. But to accommodate 24 pilgrims so that there shall be twice as many sleeping on the upper floor as on the lower floor, and eleven persons on each side of the building, it will be found necessary to leave some of the rooms empty. If, on the other hand, we try to put up 33, 36, 39 or 42 pilgrims, we shall find that in every case we are obliged to place more than three persons in some of the rooms. Thus we know that the number of pilgrims originally announced (whom, it will be remembered, it was possible to accommodate under the conditions of the Abbot) must have been 27, and that, since three more than this number were actually provided with beds, the total number of pilgrims was 30. The accompanying diagram shows how they might be arranged, and if in each instance we regard the upper floor as placed above the lower one, it will be seen that there are eleven persons on each side of the building, and twice as many above as below.

43.—The Riddle of the Tiled Hearth

The correct answer is shown in the illustration on page 196. No tile is in line (either horizontally, vertically, or diagonally) with another tile of the same design, and only three plain tiles are used. If after placing the four lions you fall into the error of placing four other tiles of another pattern, instead of only three, you will be left with four places that must be occupied by plain tiles. The secret consists in placing four of one kind and only three of each of the others.

44.—The Riddle of the Sack of Wine

The question was: Did Brother Benjamin take more wine from the bottle than water from the jug? Or did he take more water from the jug than wine from the bottle? He did neither. The same quantity of wine was transferred from the bottle as water was taken from the jug. Let us assume that the glass would hold a quarter of a pint. There was a pint of wine in the bottle and a pint of water in the jug. After the first manipulation the bottle contains three-quarters of a pint of wine, and the jug one pint of water mixed with a quarter of a pint of wine. Now, the second transaction consists in taking away a fifth of the contents of the jug—that is, one-fifth of a pint of water mixed with one-fifth of a quarter of a pint of wine. We thus leave behind in the jug four-fifths of a quarter of a pint of wine—that is, one-fifth of a pint—while we transfer from the jug to the bottle an equal quantity (one-fifth of a pint) of water.

45.—The Riddle of the Cellarer

There were 100 pints of wine in the cask, and on thirty occasions John the Cellarer had stolen a pint and replaced it with a pint of water. After the first theft the wine left in the cask would be 99 pints; after the second theft the wine in the cask would be 9801/100 pints (the square of 99 divided by 100); after the third theft there would remain 970299/10000 (the cube of 99 divided by the square of 100); after the fourth theft there would remain the fourth power of 99 divided by the cube of 100; and after the thirtieth theft there would remain in the cask the thirtieth power of 99 divided by the twenty-ninth power of 100. This by the ordinary method of calculation gives us a number composed of 59 figures to be divided by a number composed of 58 figures! But by the use of logarithms it may be quickly ascertained that the required quantity is very nearly 73-97/100 pints of wine left in the cask. Consequently the cellarer stole nearly 26.03 pints. The monks doubtless omitted the answer for the reason that they had no tables of logarithms, and did not care to face the task of making that long and tedious calculation in order to get the quantity "to a nicety," as the wily cellarer had stipulated.

By a simplified process of calculation, I have ascertained that the exact quantity of wine stolen would be

26.0299626611719577269984907683285057747323737647323555652999

pints. A man who would involve the monastery in a fraction of fifty-eight decimals deserved severe punishment.

46.—The Riddle of the Crusaders

The correct answer is that there would have been 602,176 Crusaders, who could form themselves into a square 776 by 776; and after the stranger joined their ranks, they could form 113 squares of 5,329 men—that is, 73 by 73. Or 113 × 732 – 1 = 7762. This is a particular case of the so-called "Pellian Equation," respecting which see A. in M., p. 164.

47.—The Riddle of St. Edmondsbury

The reader is aware that there are prime numbers and composite whole numbers. Now, 1,111,111 cannot be a prime number, because if it were the only possible answers would be those proposed by Brother Benjamin and rejected by Father Peter. Also it cannot have more than two factors, or the answer would be indeterminate. As a matter of fact, 1,111,111 equals 239 x 4649 (both primes), and since each cat killed more mice than there were cats, the answer must be 239 cats. See also the Introduction, p. 18.

Treated generally, this problem consists in finding the factors, if any, of numbers of the form (10n – 1)/9.

Lucas, in his L'Arithmétique Amusante, gives a number of curious tables which he obtained from an arithmetical treatise, called the Talkhys, by Ibn Albanna, an Arabian mathematician and astronomer of the first half of the thirteenth century. In the Paris National Library are several manuscripts dealing with the Talkhys, and a commentary by Alkalaçadi, who died in 1486. Among the tables given by Lucas is one giving all the factors of numbers of the above form up to n = 18. It seems almost inconceivable that Arabians of that date could find the factors where n = 17, as given in my Introduction. But I read Lucas as stating that they are given in Talkhys, though an eminent mathematician reads him differently, and suggests to me that they were discovered by Lucas himself. This can, of course, be settled by an examination of Talkhys, but this has not been possible during the war.

The difficulty lies wholly with those cases where n is a prime number. If n = 2, we get the prime 11. The factors when n = 3, 5, 11, and 13 are respectively (3 . 37), (41 . 271), (21,649 . 513,239), and (53 . 79 . 265371653). I have given in these pages the factors where n = 7 and 17. The factors when n= 19, 23, and 37 are unknown, if there are any.2 When n = 29, the factors are (3,191 . 16,763 . 43,037. 62,003 . 77,843,839,397); when n = 31, one factor is 2,791; and when n = 41, two factors are (83 . 1,231).

As for the even values of n, the following curious series of factors will doubtless interest the reader. The numbers in brackets are primes.

n = 2 = (11)

n = 6 = (11) × 111 × 91

n = 10 = (11) × 11,111 × (9,091)

n = 14 = (11) × 1,111,111 × (909,091)

n = 18 = (11) × 111,111,111 × 90,909,091

Or we may put the factors this way:—

n = 2 = (11)

n = 6 = 111 × 1,001

n = 10 = 11,111 × 100,001

n = 14 = 1,111,111 × 10,000,001

n = 18 = 111,111,111 × 1,000,000,001

In the above two tables n is of the form 4m + 2. When n is of the form 4m the factors may be written down as follows:—

n= 4 = (11) × (101)

n = 8 = (11) × (101) × 10,001

n = 12 = (11) × (101) × 100,010,001

n = 16 = (11) × (101) × 1,000,100,010,001.

When n = 2, we have the prime number 11; when n = 3, the factors are 3 . 37; when n = 6, they are 11 . 3 . 37 . 7. 13; when n = 9, they are 32 . 37 . 333,667. Therefore we know that factors of n = 18 are 11. 32 . 37 . 7 . 13 . 333,667, while the remaining factor is composite and can be split into 19 . 52579. This will show how the working may be simplified when n is not prime.

48.—The Riddle of the Frogs' Ring

The fewest possible moves in which this puzzle can be solved are 118. I will give the complete solution. The black figures on white discs move in the directions of the hands of a clock, and the white figures on black discs the other way. The following are the numbers in the order in which they move. Whether you have to make a simple move or a leaping move will be clear from the position, as you never can have an alternative. The moves enclosed in brackets are to be played five times over: 6, 7, 8, 6, 5, 4, 7, 8, 9, 10, 6, 5, 4, 3, 2, 7, 8, 9, 10, 11 (6, 5, 4, 3, 2, 1), 6, 5, 4, 3, 2, 12, (7, 8, 9, 10, 11, 12), 7, 8, 9, 10, 11, 1, 6, 5, 4, 3, 2, 12, 7, 8, 9, 10, 11, 6, 5, 4, 3, 2, 8, 9, 10, 11, 4, 3, 2, 10, 11, 2. We thus have made 118 moves within the conditions, the black frogs have changed places with the white ones, and 1 and 12 are side by side in the positions stipulated.

The general solution in the case of this puzzle is 3n2 + 2n – 2 moves, where the number of frogs of each colour is n. The law governing the sequence of moves is easily discovered by an examination of the simpler cases, where n = 2, 3, and 4.

If, instead of 11 and 12 changing places, the 6 and 7 must interchange, the expression is n2 + 4n + 2 moves. If we give n the value 6, as in the example of the Frogs' Ring, the number of moves would be 62.

For a general solution of the case where frogs of one colour reverse their order, leaving the blank space in the same position, and each frog is allowed to be moved in either direction (leaping, of course, over his own colour), see "The Grasshopper Puzzle" in A. in M., p. 193.

THE STRANGE ESCAPE OF THE KING'S JESTER

Although the king's jester promised that he would "thereafter make the manner thereof plain to all," there is no record of his having ever done so. I will therefore submit to the reader my own views as to the probable solutions to the mysteries involved.

49.—The Mysterious Rope

When the jester "divided his rope in half," it does not follow that he cut it into two parts, each half the original length of the rope. No doubt he simply untwisted the strands, and so divided it into two ropes, each of the original length, but one-half the thickness. He would thus be able to tie the two together and make a rope nearly twice the original length, with which it is quite conceivable that he made good his escape from the dungeon.

50.—The Underground Maze

How did the jester find his way out of the maze in the dark? He had simply to grope his way to a wall and then keep on walking without once removing his left hand (or right hand) from the wall. Starting from A, the dotted line will make the route clear when he goes to the left. If the reader tries the route to the right in the same way he will be equally successful; in fact, the two routes unite and cover every part of the walls of the maze except those two detached parts on the left-hand side—one piece like a U, and the other like a distorted E. This rule will apply to the majority of mazes and puzzle gardens; but if the centre were enclosed by an isolated wall in the form of a split ring, the jester would simply have gone round and round this ring.

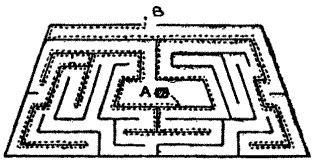
See the article, "Mazes, and How to Thread Them," in A. in M.

51.—The Secret Lock

This puzzle entailed the finding of an English word of three letters, each letter being found on a different dial. Now, there is no English word composed of consonants alone, and the only vowel appearing anywhere on the dials is Y. No English word begins with Y and has the two other letters consonants, and all the words of three letters ending in Y (with two consonants) either begin with an S or have H, L, or R as their second letter. But these four consonants do not appear. Therefore Y must occur in the middle, and the only word that I can find is "PYX," and there can be little doubt that this was the word. At any rate, it solves our puzzle.

52.—Crossing the Moat

No doubt some of my readers will smile at the statement that a man in a boat on smooth water can pull himself across with the tiller rope! But it is a fact. If the jester had fastened the end of his rope to the stern of the boat and then, while standing in the bows, had given a series of violent jerks, the boat would have been propelled forward. This has often been put to a practical test, and it is said that a speed of two or three miles an hour may be attained. See W. W. Rouse Ball's Mathematical Recreations.

53.—The Royal Gardens

This puzzle must have struck many readers as being absolutely impossible. The jester said: "I had, of a truth, entered every one of the sixteen gardens once, and never more than once." If we follow the route shown in the accompanying diagram, we find that there is no difficulty in once entering all the gardens but one before reaching the last garden containing the exit B. The difficulty is to get into the garden with a star, because if we leave the B garden we are compelled to enter it a second time before escaping, and no garden may be entered twice. The trick consists in the fact that you may enter that starred garden without necessarily leaving the other. If, when the jester got to the gateway where the dotted line makes a sharp bend, his intention had been to hide in the starred garden, but after he had put one foot through the doorway, upon the star, he discovered it was a false alarm and withdrew, he could truly say: "I entered the starred garden, because I put my foot and part of my body in it; and I did not enter the other garden twice, because, after once going in I never left it until I made my exit at B." This is the only answer possible, and it was doubtless that which the jester intended.

See "The Languishing Maiden," in A. in M.

54.—Bridging the Ditch

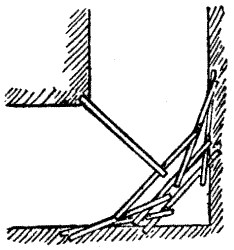
The solution to this puzzle is best explained by the illustration. If he had placed his eight planks, in the manner shown, across the angle of the ditch, he would have been able to cross without much trouble. The king's jester might thus have well overcome all his difficulties and got safely away, as he has told us that he succeeded in doing.

THE SQUIRE'S CHRISTMAS PUZZLE PARTY

HOW THE VARIOUS TRICKS WERE DONE

The record of one of Squire Davidge's annual "Puzzle Parties," made by the old gentleman's young lady relative, who had often spent a merry Christmas at Stoke Courcy Hall, does not contain the solutions of the mysteries. So I will give my own answers to the puzzles and try to make them as clear as possible to those who may be more or less novices in such matters.

55.—The Three Teacups

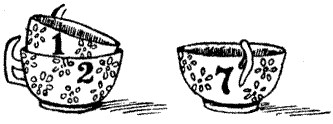
Miss Charity Lockyer clearly must have had a trick up her sleeve, and I think it highly probable that it was conceived on the following lines. She proposed that ten lumps of sugar should be placed in three teacups, so that there should be an odd number of lumps in every cup. The illustration perhaps shows Miss Charity's answer, and the figures on the cups indicate the number of lumps that have been separately placed in them. By placing the cup that holds one lump inside the one that holds two lumps, it can be correctly stated that every cup contains an odd number of lumps. One cup holds seven lumps, another holds one lump, while the third cup holds three lumps. It is evident that if a cup contains another cup it also contains the contents of that second cup.

There are in all fifteen different solutions to this puzzle. Here they are:—

The first two numbers in a triplet represent respectively the number of lumps to be placed in the inner and outer of the two cups that are placed one inside the other. It will be noted that the outer cup of the pair may itself be empty.

56.—The Eleven Pennies

It is rather evident that the trick in this puzzle was as follows:—From the eleven coins take five; then add four (to those already taken away) and you leave nine—in the second heap of those removed!

57.—The Christmas Geese

Farmer Rouse sent exactly 101 geese to market. Jabez first sold Mr. Jasper Tyler half of the flock and half a goose over (that is, 50-½ + ½, or 51 geese, leaving 50); he then sold Farmer Avent a third of what remained and a third of a goose over (that is, 16-2/3 + 1/3, or 17 geese, leaving 33); he then sold Widow Foster a quarter of what remained and three-quarters of a goose over (that is, 8-1/4 + 3/4 or 9 geese, leaving 24); he next sold Ned Collier a fifth of what he had left and gave him a fifth of a goose "for the missus" (that is, 4-4/5 + 1/5 or 5 geese, leaving 19). He then took these 19 back to his master.

58.—The Chalked Numbers