The Canterbury Puzzles, and Other Curious Problems

81.—The Eight Clowns

This is a little novelty in magic squares. These squares may be formed with numbers that are in arithmetical progression, or that are not in such progression. If a square be formed of the former class, one place may be left vacant, but only under particular conditions. In the case of our puzzle there would be no difficulty in making the magic square with 9 missing; but with 1 missing (that is, using 2, 3, 4, 5, 6, 7, 8, and 9) it is not possible. But a glance at the original illustration will show that the numbers we have to deal with are not actually those just mentioned. The clown that has a 9 on his body is portrayed just at the moment when two balls which he is juggling are in mid-air. The positions of these balls clearly convert his figure into the recurring decimal .̍9. Now, since the recurring decimal .̍9 is equal to 9/9, and therefore to 1, it is evident that, although the clown who bears the figure 1 is absent, the man who bears the figure 9 by this simple artifice has for the occasion given his figure the value of the number 1. The troupe can consequently be grouped in the following manner:—

Every column, every row, and each of the two diagonals now add up to 12. This is the correct solution to the puzzle.

82.—The Wizard's Arithmetic

This puzzle is both easy and difficult, for it is a very simple matter to find one of the multipliers, which is 86. If we multiply 8 by 86, all we need do is to place the 6 in front and the 8 behind in order to get the correct answer, 688. But the second number is not to be found by mere trial. It is 71, and the number to be multiplied is no less than 1639344262295081967213114754098360655737704918032787. If you want to multiply this by 71, all you have to do is to place another 1 at the beginning and another 7 at the end—a considerable saving of labour! These two, and the example shown by the wizard, are the only two-figure multipliers, but the number to be multiplied may always be increased. Thus, if you prefix to 41096 the number 41095890, repeated any number of times, the result may always be multiplied by 83 in the wizard's peculiar manner.

If we add the figures of any number together and then, if necessary, again add, we at last get a single-figure number. This I call the "digital root." Thus, the digital root of 521 is 8, and of 697 it is 4. This digital analysis is extensively dealt with in A. in M. Now, it is evident that the digital roots of the two numbers required by the puzzle must produce the same root in sum and product. This can only happen when the roots of the two numbers are 2 and 2, or 9 and 9, or 3 and 6, or 5 and 8. Therefore the two-figure multiplier must have a digital root of 2, 3, 5, 6, 8, or 9. There are ten such numbers in each case. I write out all the sixty, then I strike out all those numbers where the second figure is higher than the first, and where the two figures are alike (thirty-six numbers in all); also all remaining numbers where the first figure is odd and the second figure even (seven numbers); also all multiples of 5 (three more numbers). The numbers 21 and 62 I reject on inspection, for reasons that I will not enter into. I then have left, out of the original sixty, only the following twelve numbers: 83, 63, 81, 84, 93, 42, 51, 87, 41, 86, 53, and 71. These are the only possible multipliers that I have really to examine.

My process is now as curious as it is simple in working. First trying 83, I deduct 10 and call it 73. Adding 0's to the second figure, I say if 30000, etc., ever has a remainder 43 when divided by 73, the dividend will be the required multiplier for 83. I get the 43 in this way. The only multiplier of 3 that produces an 8 in the digits place is 6. I therefore multiply 73 by 6 and get 438, or 43 after rejecting the 8. Now, 300,000 divided by 73 leaves the remainder 43, and the dividend is 4,109. To this 1 add the 6 mentioned above and get 41,096 x 83, the example given on page 129.

In trying the even numbers there are two cases to be considered. Thus, taking 86, we may say that if 60000, etc., when divided by 76 leaves either 22 or 60 (because 3×6 and 8×6 both produce 8), we get a solution. But I reject the former on inspection, and see that 60 divided by 76 is 0, leaving a remainder 60. Therefore 8 x 86 = 688, the other example. It will be found in the case of 71 that 100000, etc., divided by 61 gives a remainder 42, (7 × 61 = 427) after producing the long dividend at the beginning of this article, with the 7 added.

The other multipliers fail to produce a solution, so 83, 86, and 71 are the only three possible multipliers. Those who are familiar with the principle of recurring decimals (as somewhat explained in my next note on No. 83, "The Ribbon Problem") will understand the conditions under which the remainders repeat themselves after certain periods, and will only find it necessary in two or three cases to make any lengthy divisions. It clearly follows that there is an unlimited number of multiplicands for each multiplier.

83.—The Ribbon Problem

The solution is as follows: Place this rather lengthy number on the ribbon, 0212765957446808510638297872340425531914393617. It may be multiplied by any number up to 46 inclusive to give the same order of figures in the ring. The number previously given can be multiplied by any number up to 16. I made the limit 9 in order to put readers off the scent. The fact is these two numbers are simply the recurring decimals that equal 1/17 and 1/47 respectively. Multiply the one by seventeen and the other by forty-seven, and you will get all nines in each case.

In transforming a vulgar fraction, say 1/17, to a decimal fraction, we proceed as below, adding as many noughts to the dividend as we like until there is no remainder, or until we get a recurring series of figures, or until we have carried it as far as we require, since every additional figure in a never-ending decimal carries us nearer and nearer to exactitude.

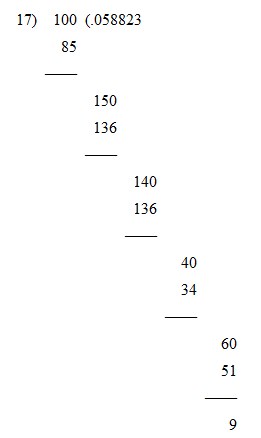
Now, since all powers of 10 can only contain factors of the powers of 2 and 5, it clearly follows that your decimal never will come to an end if any other factor than these occurs in the denominator of your vulgar fraction. Thus, ½, 1/4, and 1/8 give us the exact decimals, .5, .25, and .125; 1/5 and 1/25 give us .2 and .04; 1/10 and 1/20 give us .1 and .05: because the denominators are all composed of 2 and 5 factors. But if you wish to convert 1/3, 1/6, or 1/7, your division sum will never end, but you will get these decimals, .33333, etc., .166666, etc., and .142857142857142857, etc., where, in the first case, the 3 keeps on repeating for ever and ever; in the second case the 6 is the repeater, and in the last case we get the recurring period of 142857. In the case of 1/17 (in "The Ribbon Problem") we find the circulating period to be .0588235294117647.

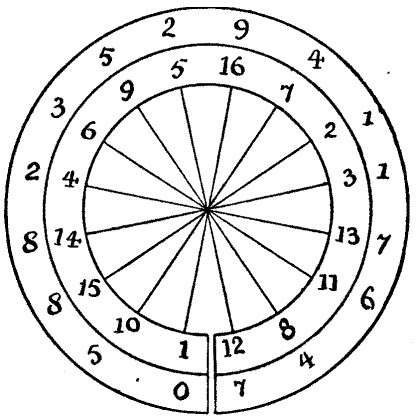
Now, in the division sum above, the successive remainders are 1, 10, 15, 14, 4, 6, 9, etc., and these numbers I have inserted around the inner ring of the diagram. It will be seen that every number from 1 to 16 occurs once, and that if we multiply our ribbon number by any one of the numbers in the inner ring its position indicates exactly the point at which the product will begin. Thus, if we multiply by 4, the product will be 235, etc.; if we multiply by 6, 352, etc. We can therefore multiply by any number from 1 to 16 and get the desired result.

The kernel of the puzzle is this: Any prime number, with the exception of 2 and 5, which are the factors of 10, will exactly divide without remainder a number consisting of as many nines as the number itself, less one. Thus 999999 (six 9's) is divisible by 7, sixteen 9's are divisible by 17, eighteen 9's by 19, and so on. This is always the case, though frequently fewer 9's will suffice; for one 9 is divisible by 3, two by 11, six by 13, when our ribbon rule for consecutive multipliers breaks down and another law comes in. Therefore, since the 0 and 7 at the ends of the ribbon may not be removed, we must seek a fraction with a prime denominator ending in 7 that gives a full period circulator. We try 37, and find that it gives a short period decimal, .027, because 37 exactly divides 999; it, therefore, will not do. We next examine 47, and find that it gives us the full period circulator, in 46 figures, at the beginning of this article.

If you cut any of these full period circulators in half and place one half under the other, you will find that they will add up all 9's; so you need only work out one half and then write down the complements. Thus, in the ribbon above, if you add 05882352 to 94117647 the result is 99999999, and so with our long solution number. Note also in the diagram above that not only are the opposite numbers on the outer ring complementary, always making 9 when added, but that opposite numbers in the inner ring, our remainders, are also complementary, adding to 17 in every case. I ought perhaps to point out that in limiting our multipliers to the first nine numbers it seems just possible that a short period circulator might give a solution in fewer figures, but there are reasons for thinking it improbable.

84.—The Japanese Ladies and the Carpet

If the squares had not to be all the same size, the carpet could be cut in four pieces in any one of the three manners shown. In each case the two pieces marked A will fit together and form one of the three squares, the other two squares being entire. But in order to have the squares exactly equal in size, we shall require six pieces, as shown in the larger diagram. No. 1 is a complete square, pieces 4 and 5 will form a second square, and pieces 2, 3, and 6 will form the third—all of exactly the same size.

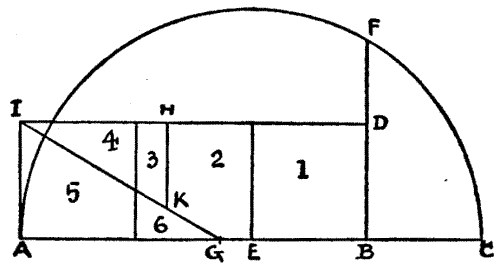
If with the three equal squares we form the rectangle IDBA, then the mean proportional of the two sides of the rectangle will be the side of a square of equal area. Produce AB to C, making BC equal to BD. Then place the point of the compasses at E (midway between A and C) and describe the arc AC. I am showing the quite general method for converting rectangles to squares, but in this particular case we may, of course, at once place our compasses at E, which requires no finding. Produce the line BD, cutting the arc in F, and BF will be the required side of the square. Now mark off AG and DH, each equal to BF, and make the cut IG, and also the cut HK from H, perpendicular to ID. The six pieces produced are numbered as in the diagram on last page.

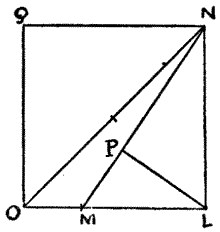
It will be seen that I have here given the reverse method first: to cut the three small squares into six pieces to form a large square. In the case of our puzzle we can proceed as follows:—

Make LM equal to half the diagonal ON. Draw the line NM and drop from L a perpendicular on NM. Then LP will be the side of all the three squares of combined area equal to the large square QNLO. The reader can now cut out without difficulty the six pieces, as shown in the numbered square on the last page.

85.—Captain Longbow and the Bears

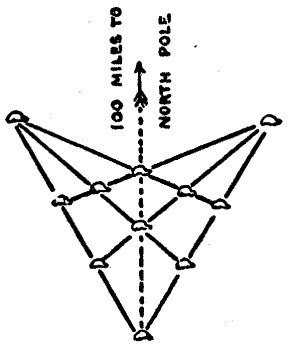
It might have struck the reader that the story of the bear impaled on the North Pole had no connection with the problem that followed. As a matter of fact it is essential to a solution. Eleven bears cannot possibly be arranged to form of themselves seven rows of bears with four bears in every row. But it is a different matter when Captain Longbow informs us that "they had so placed themselves that there were" seven rows of four bears. For if they were grouped as shown in the diagram, so that three of the bears, as indicated, were in line with the North Pole, that impaled animal would complete the seventh row of four, which cannot be obtained in any other way. It obviously does not affect the problem whether this seventh row is a hundred miles long or a hundred feet, so long as they were really in a straight line—a point that might perhaps be settled by the captain's pocket compass.

86.—The English Tour

It was required to show how a resident at the town marked A might visit every one of the towns once, and only once, and finish up his tour at Z. This puzzle conceals a little trick. After the solver has demonstrated to his satisfaction that it cannot be done in accordance with the conditions as he at first understood them, he should carefully examine the wording in order to find some flaw. It was said, "This would be easy enough if he were able to cut across country by road, as well as by rail, but he is not."

Now, although he is prohibited from cutting across country by road, nothing is said about his going by sea! If, therefore, we carefully look again at the map, we shall find that two towns, and two only, lie on the sea coast. When he reaches one of these towns he takes his departure on board a coasting vessel and sails to the other port. The annexed illustration shows, by a dark line, the complete route.

This problem should be compared with No. 250, "The Grand Tour," in A. in M. It can be simplified in practically an identical manner, but as there is here no choice on the first stage from A, the solutions are necessarily quite different. See also solution to No. 94.

87.—The Chifu-Chemulpo Puzzle

The solution is as follows. You may accept the invitation to "try to do it in twenty moves," but you will never succeed in performing the feat. The fewest possible moves are twenty-six. Play the cars so as to reach the following positions:—

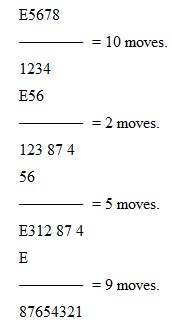
Twenty-six moves in all.

88.—The Eccentric Market-woman

The smallest possible number of eggs that Mrs. Covey could have taken to market is 719. After selling half the number and giving half an egg over she would have 359 left; after the second transaction she would have 239 left; after the third deal, 179; and after the fourth, 143. This last number she could divide equally among her thirteen friends, giving each 11, and she would not have broken an egg.

89.—The Primrose Puzzle

The two words that solve this puzzle are BLUEBELL and PEARTREE. Place the letters as follows: B 3-1, L 6-8, U 5-3, E 4-6, B 7-5, E 2-4, L 9-7, L 9-2. This means that you take B, jump from 3 to 1, and write it down on 1; and so on. The second word can be inserted in the same order. The solution depends on finding those words in which the second and eighth letters are the same, and also the fourth and sixth the same, because these letters interchange without destroying the words. MARITIMA (or sea-pink) would also solve the puzzle if it were an English word.

Compare with No. 226 in A. in M.

90.—The Round Table

Here is the way of arranging the seven men:—

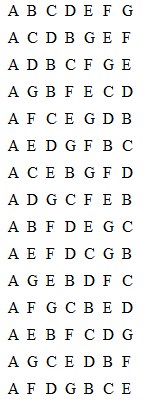
Of course, at a circular table, A will be next to the man at the end of the line.

I first gave this problem for six persons on ten days, in the Daily Mail for the 13th and 16th October 1905, and it has since been discussed in various periodicals by mathematicians. Of course, it is easily seen that the maximum number of sittings for n persons is (n – 1)(n – 2)/2 ways. The comparatively easy method for solving all cases where n is a prime+1 was first discovered by Ernest Bergholt. I then pointed out the form and construction of a solution that I had obtained for 10 persons, from which E. D. Bewley found a general method for all even numbers. The odd numbers, however, are extremely difficult, and for a long time no progress could be made with their solution, the only numbers that could be worked being 7 (given above) and 5, 9, 17, and 33, these last four being all powers of 2+1. At last, however (though not without much difficulty), I discovered a subtle method for solving all cases, and have written out schedules for every number up to 25 inclusive. The case of 11 has been solved also by W. Nash. Perhaps the reader will like to try his hand at 13. He will find it an extraordinarily hard nut.

The solutions for all cases up to 12 inclusive are given in A. in M., pp. 205, 206.

91.—The Five Tea Tins

There are twelve ways of arranging the boxes without considering the pictures. If the thirty pictures were all different the answer would be 93,312. But the necessary deductions for cases where changes of boxes may be made without affecting the order of pictures amount to 1,728, and the boxes may therefore be arranged, in accordance with the conditions, in 91,584 different ways. I will leave my readers to discover for themselves how the figures are to be arrived at.

92.—The Four Porkers

The number of ways in which the four pigs may be placed in the thirty-six sties in accordance with the conditions is seventeen, including the example that I gave, not counting the reversals and reflections of these arrangements as different. Jaenisch, in his Analyse Mathématique au jeu des Échecs (1862), quotes the statement that there are just twenty-one solutions to the little problem on which this puzzle is based. As I had myself only recorded seventeen, I examined the matter again, and found that he was in error, and, doubtless, had mistaken reversals for different arrangements.

Here are the seventeen answers. The figures indicate the rows, and their positions show the columns. Thus, 104603 means that we place a pig in the first row of the first column, in no row of the second column, in the fourth row of the third column, in the sixth row of the fourth column, in no row of the fifth column, and in the third row of the sixth column. The arrangement E is that which I gave in diagram form:—

It will be found that forms N and Q are semi-symmetrical with regard to the centre, and therefore give only two arrangements each by reversal and reflection; that form H is quarter-symmetrical, and gives only four arrangements; while all the fourteen others yield by reversal and reflection eight arrangements each. Therefore the pigs may be placed in (2 × 2) + (4 × 1) + (8 × 14) = 120 different ways by reversing and reflecting all the seventeen forms.

Three pigs alone may be placed so that every sty is in line with a pig, provided that the pigs are not forbidden to be in line with one another; but there is only one way of doing it (if we do not count reversals as different), as follows: 105030.

93.—The Number Blocks

Arrange the blocks so as to form the two multiplication sums 915 × 64 and 732 × 80, and the product in both cases will be the same: 58,560.

94.—Foxes and Geese

The smallest possible number of moves is twenty-two—that is, eleven for the foxes and eleven for the geese. Here is one way of solving the puzzle:

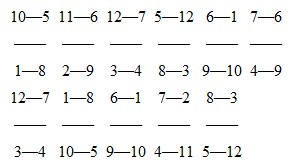
Of course, the reader will play the first move in the top line, then the first move in the second line, then the second move in the top line, and so on alternately.

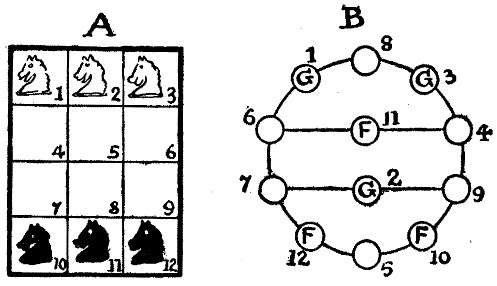
In A. in M., p. 230, I have explained fully my "buttons and string" method of solving puzzles on chequered boards. In Diagram A is shown the puzzle in the form in which it may be presented on a portion of the chessboard with six knights. A comparison with the illustration on page 141 will show that I have there dispensed with the necessity of explaining the knight's move to the uninstructed reader by lines that indicate those moves. The two puzzles are the same thing in different dress. Now compare page 141 with Diagram B, and it will be seen that by disentangling the strings I have obtained a simplified diagram without altering the essential relations between the buttons or discs. The reader will now satisfy himself without any difficulty that the puzzle requires eleven moves for the foxes and eleven for the geese. He will see that a goose on 1 or 3 must go to 8, to avoid being one move from a fox and to enable the fox on 11 to come on to the ring. If we play 1—8, then it is clearly best to play 10—5 and not 12—5 for the foxes. When they are all on the circle, then they simply promenade round it in a clockwise direction, taking care to reserve 8—3 and 5—12 for the final moves. It is thus rendered ridiculously easy by this method. See also notes on solutions to Nos. 13 and 85.

95.—Robinson Crusoe's Table

The diagram shows how the piece of wood should be cut in two pieces to form the square table-top. A, B, C, D are the corners of the table. The way in which the piece E fits into the piece F will be obvious to the eye of the reader. The shaded part is the wood that is discarded.

96.—The Fifteen Orchards

The number must be the least common multiple of 1, 2, 3, etc., up to 15, that, when divided by 7, leaves the remainder 1, by 9 leaves 3, by 11 leaves 10, by 13 leaves 3, and by 14 leaves 8. Such a number is 120. The next number is 360,480, but as we have no record of a tree—especially a very young one—bearing anything like such a large number of apples, we may take 120 to be the only answer that is acceptable.

97.—The Perplexed Plumber

The rectangular closed cistern that shall hold a given quantity of water and yet have the smallest possible surface of metal must be a perfect cube—that is, a cistern every side of which is a square. For 1,000 cubic feet of water the internal dimensions will be 10 ft. × 10 ft. × 10 ft., and the zinc required will be 600 square feet. In the case of a cistern without a top the proportions will be exactly half a cube. These are the "exact proportions" asked for in the second case. The exact dimensions cannot be given, but 12.6 ft. × 12.6 ft. × 6.3 ft. is a close approximation. The cistern will hold a little too much water, at which the buyer will not complain, and it will involve the plumber in a trifling loss not worth considering.

98.—The Nelson Column

If you take a sheet of paper and mark it with a diagonal line, as in Figure A, you will find that when you roll it into cylindrical form, with the line outside, it will appear as in Figure B.

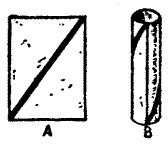
It will be seen that the spiral (in one complete turn) is merely the hypotenuse of a right-angled triangle, of which the length and width of the paper are the other two sides. In the puzzle given, the lengths of the two sides of the triangle are 40 ft. (one-fifth of 200 ft.) and 16 ft. 8 in. Therefore the hypotenuse is 43 ft. 4 in. The length of the garland is therefore five times as long—216 ft. 8 in. A curious feature of the puzzle is the fact that with the dimensions given the result is exactly the sum of the height and the circumference.