The Way To Geometry

On the same part or side it is sayd, least any man might understand right lines knit together by opposite bounds as here.

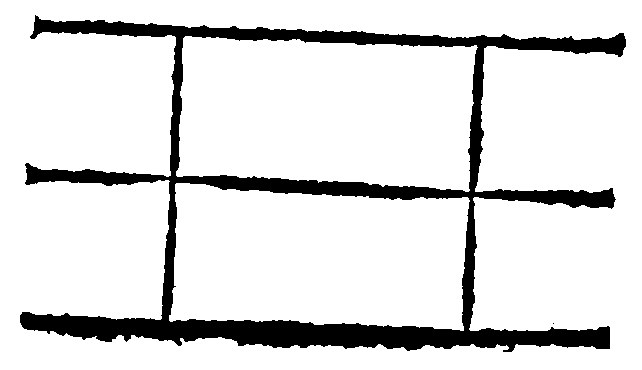
28. If right lines be cut joyntly by many parallell right lines, the segments betweene those lines shall bee proportionall one to another, out of the 2 p vj and 17 p xj.

Thus much of the Perpendicle, and parallell equality of plaine right lines: Their Proportion is the last thing to be considered of them.

The truth of this element dependeth upon the nature of the parallells: And that throughout all kindes of equality and inequality, both greater and lesser. For if the lines thus cut be perpendiculars, the portions intercepted betweene the two parallels shall be equall: for common perpendiculars doe make parallell equality, as before hath beene taught, and here thou seest.

If the lines cut be not parallels, but doe leane one toward another, the portions cut or intercepted betweene them will not be equall, yet shall they be proportionall one to another. And looke how much greater the line thus cut is: so much greater shall the intersegments or portions intercepted be. And contrariwise, Looke how much lesse: so much lesser shall they be.

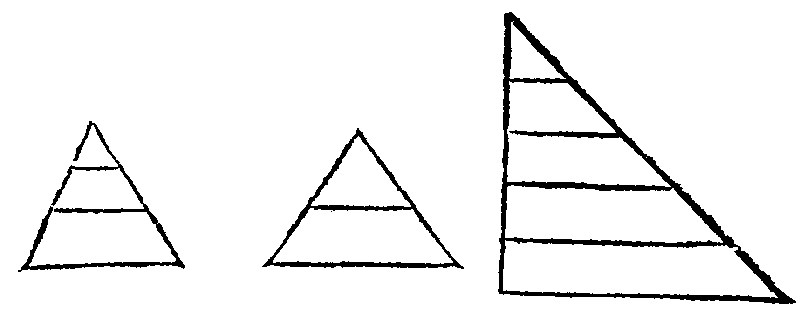
The third parallell in the toppe is not expressed, yet must it be understood.

This element is very fruitfull: For from hence doe arise and issue, First the manner of cutting a line according to any rate or proportion assigned: And then the invention or way to finde out both the third and fourth proportionalls.

29. If a right line making an angle with another right line, be cut according to any reason [or proportion] assigned, parallels drawne from the ends of the segments, unto the end of the sayd right line given and unto some contingent point in the same, shall cut the line given according to the reason given.

Schoner hath altered this Consectary, and delivereth it thus: If a right line making an angle with a right line given, and knit unto it with a base, be cut according to any rate assigned, a parallell to the base from the ends of the segments, shall cut the line given according to the rate assigned. 9 and 10 p vj.

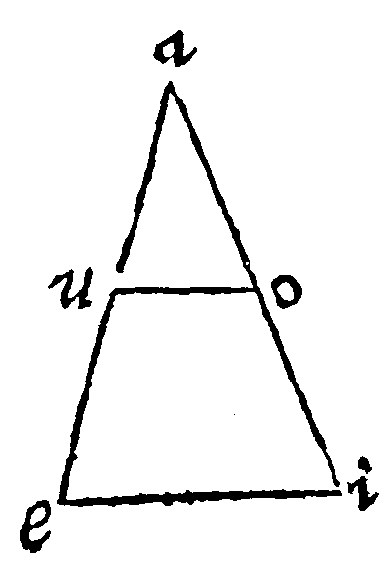
Punctum contingens, A contingent point, that is falling or lighting in some place at al adventurs, not given or assigned.

This is a marvelous generall consectary, serving indifferently for any manner of section of a right line, whether it be to be cut into two parts, or three parts, or into as many parts, as you shall thinke good, or generally after what manner of way soever thou shalt command or desire a line to be cut or divided.

Let the assigned Right line to be cut into two equall parts be ae. And the right line making an angle with it, let it be the infinite right line ai. Let ao, one portion thereof be cut off. And then by the 7 e, let oi, another part thereof be taken equall to it. And lastly, by the 24 e, draw parallels from the points i, and o, unto e, the end of the line given, and to u; a contingent point therein. Now the third parallell is understood by the point a, neither is it necessary that it should be expressed. Therefore the line ae, by the 28, is cut into two equall portions: And as ao, is to oi: So is au, to ue. But ao, and oi, are halfe parts. Therefore au, and ue, are also halfe parts.

And here also is the 12 e comprehended, although not in the same kinde of argument, yet in effect the same. But that argument was indeed shorter, although this be more generall.

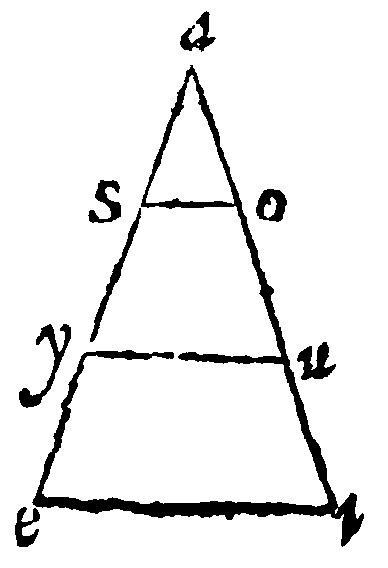
Now let ae be cut into three parts, of which the first let it bee the halfe of the second: And the second, the halfe of the third: And the conterminall or right line making an angle with the sayd assigned line, let it be cut one part ao: Then double this in ou: Lastly let ui be taken double to ou, and let the whole diagramme be made up with three parallels ie, uy, and os, The fourth parallell in the toppe, as afore-sayd, shall be understood. Therefore that section which was made in the conterminall line, by the 28 e, shall be in the assigned line: Because the segments or portions intercepted are betweene the parallels.

And

30. If two right lines given, making an angle, be continued, the first equally to the second, the second infinitly, parallels drawne from the ends of the first continuation, unto the beginning of the second, and some contingent point in the same, shall intercept betweene them the third proportionall. 11. p vj.

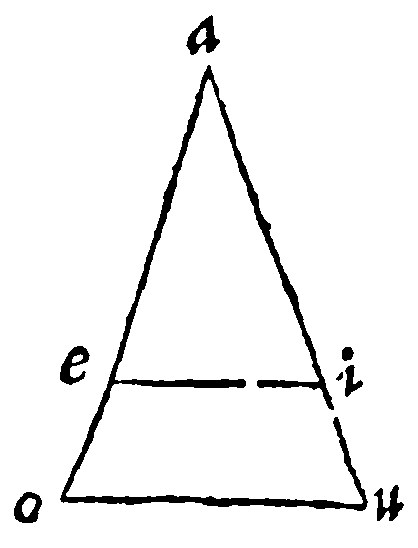
Let the right lines given, making an angle, be ae, and ai: and ae, the first, let it be continued equally to the same ai, and the same ai, let it be drawne out infinitly: Then the parallels ei, and ou, drawne from the ends of the first continuation, unto i, the beginning of the second: and u, a contingent point in the second, doe cut off iu, the third proportionall sought. For by the 28 e, as ae, is unto eo, so is ai, unto iu.

And

31. If of three right lines given, the first and the third making an angle be continued, the first equally to the second, and the third infinitly; parallels drawne from the ends of the first continuation, unto the beginning of the second, and some contingent point, the same shall intercept betweene them the fourth proportionall. 12. p vj.

Let the lines given be these: The first ae, the second ei, the third ao, and let the whole diagramme be made up according to the prescript of the consectary. Here by 28. e, as ae, is to ei so is ao, to ou. Thus farre Ramus.

Lazarus Schonerus, who, about some 25. yeares since, did revise and augment this worke of our Authour, hath not onely altered the forme of these two next precedent consectaries: but he hath also changed their order, and that which is here the second, is in his edition the third: and the third here, is in him the second. And to the former declaration of them, hee addeth these words: From hence, having three lines given, is the invention of the fourth proportionall; and out of that, having two lines given, ariseth the invention of the third proportionall.

2 Having three right lines given, if the first and the third making an angle, and knit together with a base, be continued, the first equally to the second; the third infinitly; a parallel from the end of the second, unto the continuation of the third, shall intercept the fourth proportionall. 12. p vj.

The Diagramme, and demonstration is the same with our 31. e or 3 c of Ramus.

3 If two right lines given making an angle, and knit together with a base, be continued, the first equally to the second, the second infinitly; a parallell to the base from the end of the first continuation unto the second, shall intercept the third proportionall. 11. p vj.

The Diagramme here also, and demonstration is in all respects the same with our 30 e, or 2 c of Ramus.

Thus farre Ramus: And here by the judgement of the learned Finkius, two elements of Ptolomey are to be adjoyned.

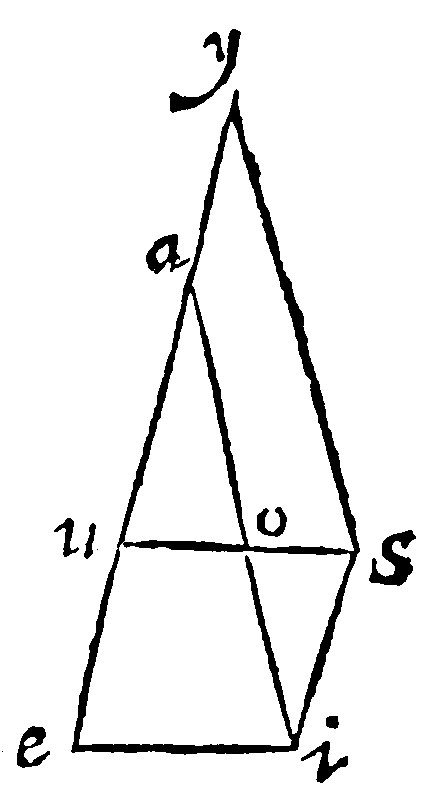
32 If two right lines cutting one another, be againe cut with many parallels, the parallels are proportionall unto their next segments.

It is a consectary out of the 28 e. For let the right lines ae. and ai, cut one another at a, and let two parallell lines uo, and ei, cut them; I say, as au, is to uo, so ae, is to ei. For from the end i, let is, be erected parallell to ae, and let uo, be drawne out untill it doe meete with it. Then from the end s, let sy, be made parallell to ai: and lastly, let ea, be drawne out, untill it doe meete with it. Here now ay, shall be equall to the right line is, that is, by the 26. e, to ue: and at length, by the 28. e, as ua, is to uo; so is ay, that is, ue, to os. Therefore, by composition or addition of proportions, as ua, is unto uo, so ua, and ue, shall be unto uo, and os, that is, ei, by the 27. e.

The same demonstration shall serve, if the lines do crosse one another, or doe vertically cut one another, as in the same diagramme appeareth. For if the assigned ai, and us, doe cut one another vertically in o, let them be cut with the parallels au, and si: the precedent fabricke or figure being made up, it shall be by 28. e. as au, is unto ao, the segment next unto it: so ay, that is, is, shall be unto oi, his next segment.

The 28. e teacheth how to finde out the third and fourth proportionall: This affordeth us a meanes how to find out the continually meane proportionall single or double.

Therefore

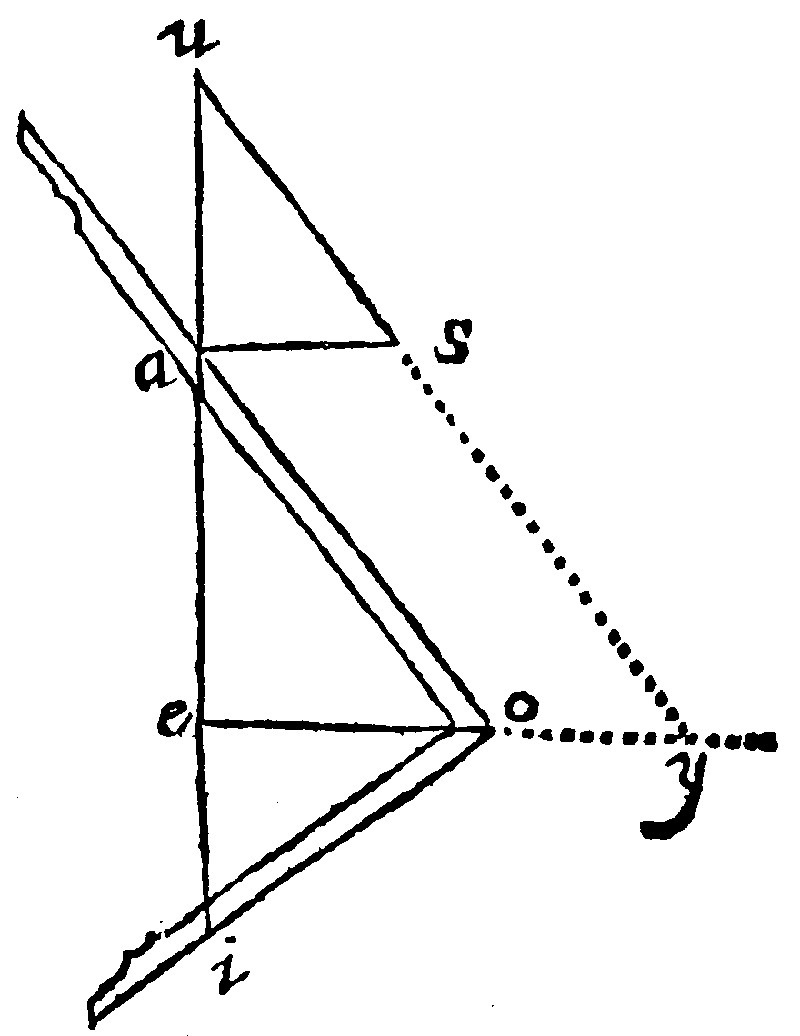
33. If two right lines given be continued into one, a perpendicular from the point of continuation unto the angle of the squire, including the continued line with the continuation, is the meane proportionall betweene the two right lines given.

A squire (Norma, Gnomon, or Canon) is an instrument consisting of two shankes, including a right angle. Of this we heard before at the 13. e. By the meanes of this a meane proportionall unto two lines given is easily found: whereupon it may also be called a Mesolabium, or Mesographus simplex, or single meane finder.

Let the two right lines given, be ae, and ei. The meane proportional between these two is desired. For the finding of which, let it be granted that as ae, is to eo, so eo, is to ei: therefore let ae, be continued or drawne out unto i, so that ei, be equall to the other given. Then from e, the point of the continuation, let eo, an infinite perpendicular be erected. Now about this perpendicular, up and downe, this way and that way, let the squire ao, be moved, so that with his angle it may comprehend at eo, and with his shanks it may include the whole right line ai. I say that eo, the segment of the perpendicular, is the meane proportionall between ae, and ei, the two lines given. For let ea, be continued or drawne out into u, so that the continuation au, be equall unto eo: and unto a, the point of the continuation, let the angle uas, be made equall, and equicrurall to the angle oei, that is, let the shanke as, be made equall to the shanke ei. Wherefore knitting u, and s, together, the right lines us, and oi, shall be equall; and the angles eoi, aus, by the 7. e iij. And by the 21. e, the lines sa, and oe, are parallell: and the angle sao, is equall to the angle aoe. But the angles sae, and aoi, are right angles by the Fabricke and by the grant; and therefore they are equall, by the 14. e iij. Wherefore the other angles oae, and eoi, that is, sua, are equall. And therefore by the 21. e. us, and ao are parallell; and us, and eo, continued shall meete, as here in y: and by the 26. e. oy, and as are equall. Now, by the 32. e. as ue, is to ua, so is ey, to as. Therefore by subduction or subtraction of proportions, as ea, is to ua, so is eo, that is, ua, to oy, that is as.

And

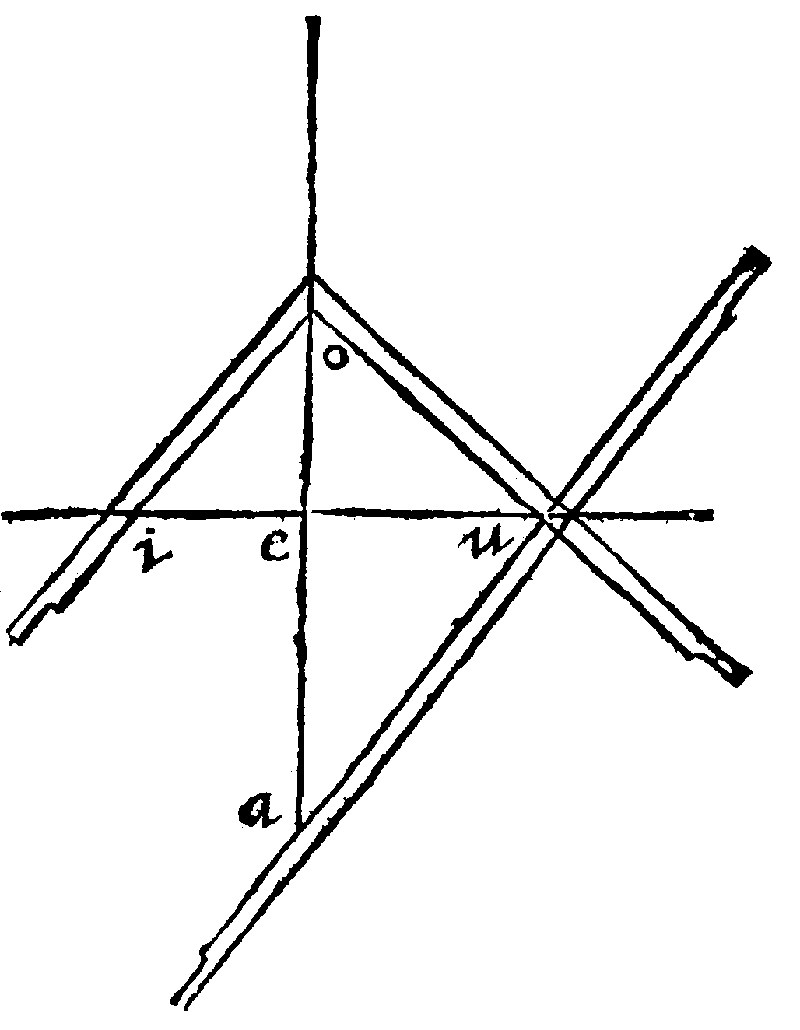
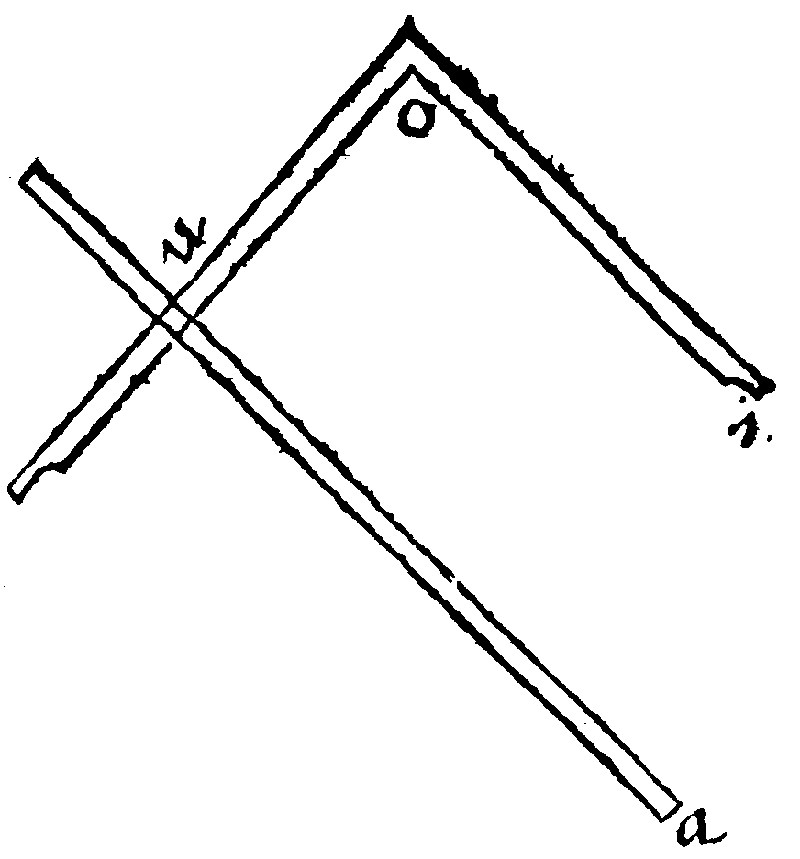
34 If two assigned right lines joyned together by their ends rightanglewise, be continued vertically; a square falling with one of his shankes, and another to it parallell and moveable upon the ends of the assigned, with the angles upon the continued lines, shall cut betweene them from the continued two meanes continually proportionall to the assigned.

The former consectary was of a single mesolabium; this is of a double, whose use in making of solids, to this or that bignesse desired is notable.

Let the two lines assigned be ae, and ei; and let there be two meane right lines, continually proportionall betweene them sought, to wit, that may be as ae, is unto one of the lines found; so the same may be unto the second line found. And as that is unto this, so this may be unto ei. Let therefore ae, and ei, be joyned rightanglewise by their ends at e; and let them be infinite continued, but vertically, that is, from that their meeting from the lines ward, from ei, towards u, but ae, towards o. Now for the rest, the construction; it was Plato's Mesographus; to wit, a squire with the opposits parallell. One of his sides au, moueable, or to be done up and downe, by an hollow riglet in the side adjoyning. Therefore thou shalt make thee a Mesographus, if unto the squire thou doe adde one moveable side, but so that how so ever it be moved, it be still parallell unto the opposite side [which is nothing else, but as it were a double squire, if this squire be applied unto it; and indeed what is done by this instrument, may also be done by two squires, as hereafter shall be shewed.] And so long and oft must the moveable side be moved up and downe, untill with the opposite side it containe or touch the ends of the assigned, but the angles must fall precisely upon the continued lines: The right lines from the point of the continuation, unto the corners of the squire, are the two meane proportionals sought.

As if of the Mesographus auoi, the moveable side be au; thus thou shalt move up and downe, untill the angles u, and o, doe hit just upon the infinite lines; and joyntly at the same instant ua, and oi, may touch the ends of the assigned a, and i. By the former consectary it shall be as ei, is to eo, so eo, shall be unto eu: and as eo, is to eu, so shall eu, be unto ea.

And thus wee have the composition and use, both of the single and double Mesolabium.

35. If of foure right lines, two doe make an angle, the other reflected or turned backe upon themselves, from the ends of these, doe cut the former; the reason of the one unto his owne segment, or of the segments betweene themselves, is made of the reason of the so joyntly bounded, that the first of the makers be joyntly bounded with the beginning of the antecedent made; the second of this consequent joyntly bounded with the end; doe end in the end of the consequent made.

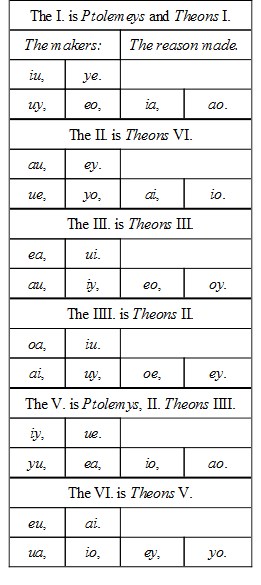
Ptolomey hath two speciall examples of this Theorem: to those Theon addeth other foure.

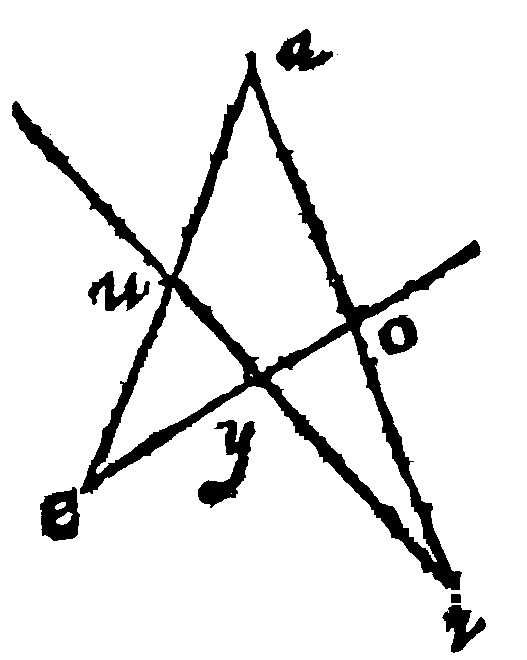
Let therefore the two right lines be ae, and ai: and from the ends of these other two reflected, be iu, and eo, cutting themselves in y; and the two former in u, and o. The reason of the particular right lines made shall be as the draught following doth manifest. In which the antecedents of the makers are in the upper place: the consequents are set under neathe their owne antecedents.

The businesse is the same in the two other, whether you doe crosse the bounds or invert them.

Here for demonstrations sake we crave no more, but that from the beginning of an antecedent made a parallell be drawne to the second consequent of the makers, unto one of the assigned infinitely continued: then the multiplied proportions shall be,

The Antecedent, the Consequent; the Antecedent, the Consequent of the second of the makers; every way the reason or rate is of Equallity.

The Antecedent; the Consequent of the first of the makers; the Parallell; the Antecedent of the second of the makers, by the 32. e. Therefore by multiplication of proportions, the reason of the Parallell, unto the Consequent of the second of the makers, that is, by the fabricke or construction, and the 32. e. the reason of the Antecedent of the Product, unto the Consequent, is made of the reason, &c. after the manner above written.

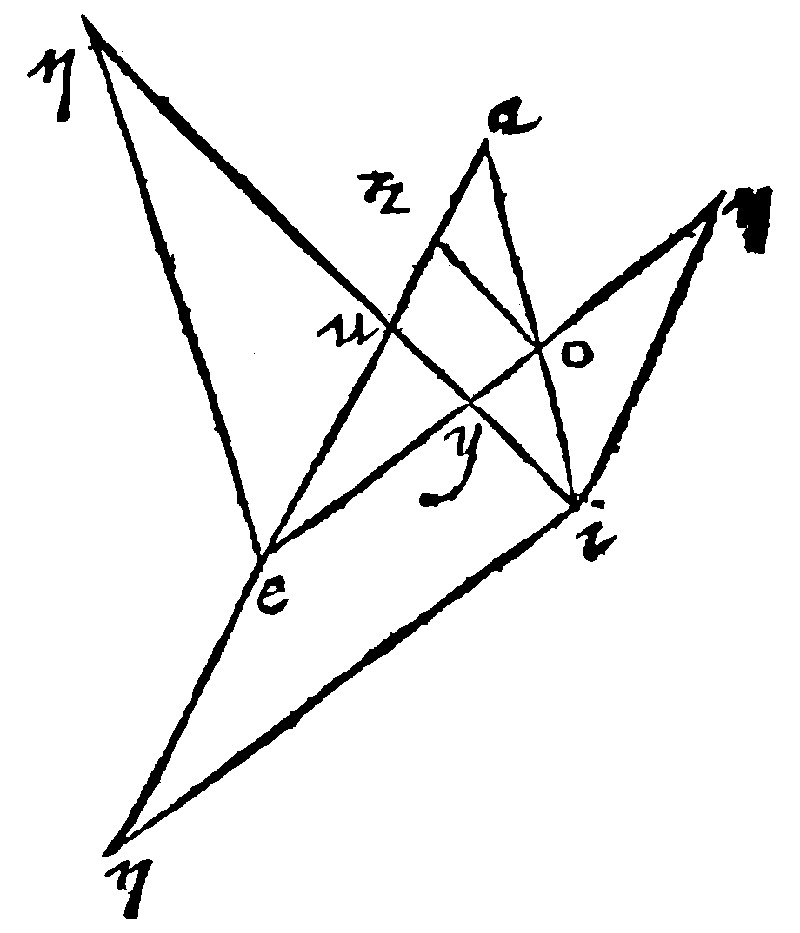
For examples sake, let the first speciall example be demonstrated. I say therefore, that the reason of ia, unto ao, is made of the reason of iu, unto uy, multiplied by the reason of ye, unto eo. For from the beginning of the Antecedent of the product, to wit, from the point i, let a line be drawne parallell to the right line ey, which shall meete with ae, continued or drawne out infinitely in n. Therefore, by the 32. e, as ia, is to ao: so is the parallell drawne to eo, the Consequent of the second of the makers. Therefore now the multiplied proportions are thus iu, uy, in, ey, by the 32. e: ye, eo, ey, eo. Therefore as the product of iu, by ye, is unto the product of uy, by eo: So in, is to eo, that is, ia, to ao.

So let the second of Ptolemy to be taught, which in our Table aforegoing is the fifth. I say therefore that the reason of io, unto oa; is made of the reason of iy, unto yu, and the reason of ue, unto ea. For now againe, from the beginning of the Antecedent of the Product i, let a line be drawne parallell unto ea, the Consequent of the second of the Makers, which shall meete with eo, drawne out at length, in n: therefore, by the 32. e. as io, is to ao; so is en, unto ea. Therefore now again the multiplied proportions are thus:

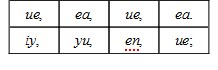
by the 32. e. Therefore, by multiplication of proportions, the reason of en, unto ea, that is, of io, unto oa, is made of the reason of iy, unto yu, by the reason of ue, unto ea.

It shall not be amisse to teach the same in the examples of Theon. Let us take therefore the reason of the Reflex, unto the Segment; And of the segments betweene themselves; to wit, the 4. and 6. examples of our foresaid draught: I say therefore, that the reason of oe, unto ey, is made of the reason oa, unto ai, by the reason of iu, unto uy. For from the end o, to wit, from the beginning of the Antecedent of the product, let the right line no, be drawne parallell to uy. It shall be by the 32. e. as oe, is to ey: so the parallell no, shall be to uy: but the reason of no, unto uy, is made of the reason of oa, unto ai, and of iu, unto uy: for the multiplied proportions are,

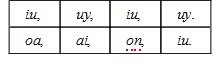
by the 32. e.

Againe, I say, that the reason of ey, unto yo, is compounded of the reason of eu, unto ua, and of ai, unto io.

Theon here draweth a parallell from o, unto ui. By the generall fabricke it may be drawne out of e, unto ui.

It shall be therefore as ey, is unto yo, so en, shall be unto oi. Now the proportions multiplied are,

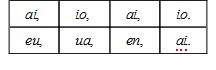
by the 32. e.

Therefore the reason of en, unto io , that is of ey, unto yo, shall be made of the foresaid reasons.

Of the segments of divers right lines, the Arabians have much under the name of The rule of sixe quantities. And the Theoremes of Althindus, concerning this matter, are in many mens hands. And Regiomontanus in his Algorithmus: and Maurolycus upon the 1 p iij. of Menelaus, doe make mention of them; but they containe nothing, which may not, by any man skillfull in Arithmeticke, be performed by the multiplication of proportions. For all those wayes of theirs are no more but speciall examples of that kinde of multiplication.

Of Geometry, the sixt Booke, of a Triangle

1. Like plaines have a double reason of their homologall sides, and one proportionall meane, out of 20 p vj. and xj. and 18. p viij.

Or thus; Like plaines have the proportion of their correspondent proportionall sides doubled, & one meane proportionall: Hitherto wee have spoken of plaine lines and their affections: Plaine figures and their kindes doe follow in the next place. And first, there is premised a common corollary drawne out of the 24. e. iiij. because in plaines there are but two dimensions.

2. A plaine surface is either rectilineall or obliquelineall, [or rightlined, or crookedlined. H.]

Straightnesse, and crookednesse, was the difference of lines at the 4. e. ij. From thence is it here repeated and attributed to a surface, which is geometrically made of lines. That made of right lines, is rectileniall: that which is made of crooked lines, is Obliquilineall.

3. A rectilineall surface, is that which is comprehended of right lines.

A plaine rightlined surface is that which is on all sides inclosed and comprehended with right lines. And yet they are not alwayes right betweene themselves, but such lines as doe lie equally betweene their owne bounds, and without comparison are all and every one of them right lines.

4. A rightilineall doth make all his angles equall to right angles; the inner ones generally to paires from two forward: the outter always to foure.

Or thus: A right lined plaine maketh his angles equall unto right angles: Namely the inward angles generally, are equall unto the even numbers from two forward, but the outward angles are equall but to 4. right angles. H.

The first kinde I meane of rectilineals, that is a triangle doth make all his inner angles equall to two right angles, that is, to a binary, the first even number of right angles: the second, that is a quadrangle, to the second even number, that is, to a quaternary or foure: The third, that is, a Pentangle, of quinqueangle to the third, that is a senary of right angles, or 6. and so farre forth as thou seest in this Arithmeticall progression of even numbers,