The Way To Geometry

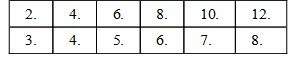
Notwithstanding the outter angles, every side continued and drawne out, are alwayes equall to a quaternary of right angles, that is to foure. The former part being granted (for that is not yet demonstrated) the latter is from thence concluded: For of the inner angles, that of the outter, is easily proved. For the three angles of a triangle are equall to two right angles. The foure of a quadrangle to foure: of a quinquangle, to sixe: of a sexe angle, to eight: Of septangle, to tenne, and so forth, form a binarie by even numbers: Whereupon, by the 14. e. V. a perpetuall quaternary of the outer angles is concluded.

5. A rectilineall is either a Triangle or a Triangulate.

As before of a line was made a lineate: so here in like manner of a triangle is made a triangulate.

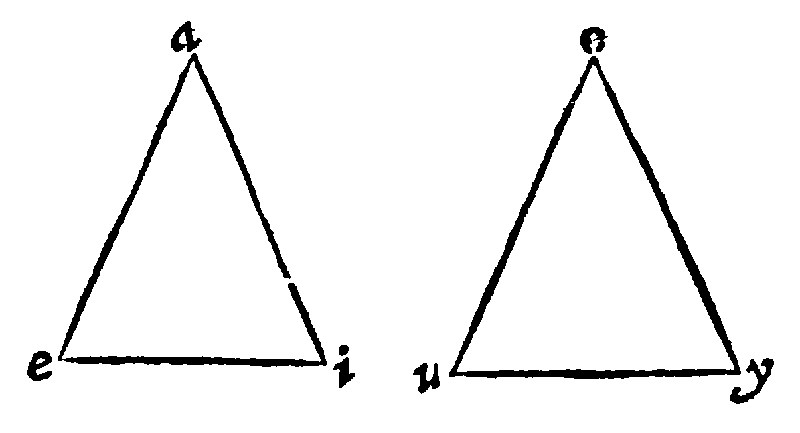
6. A triangle is a rectilineall figure comprehended of three rightlines. 21. d j.

As here aei. A triangular figure is of Euclide defined from the three sides; whereupon also it might be called Trilaterum, that is three sided, of the cause: rather than Trianglum, three cornered, of the effect; especially seeing that three angles, and three sides are not reciprocall or to be converted. For a triangle may have foure sides, as is Acidoides, or Cuspidatum, the barbed forme, which Zonodorus called Cœlogonion, or Cavangulum, an hollow cornered figure. It may also have both five, and sixe sides, as here thou seest. The name therefore of Trilaterum would more fully and fitly expresse the thing named: But use hath received and entertained the name of a triangle for a trilater: And therefore let it be still retained, but in that same sense:

7. A triangle is the prime figure of rectilineals.

A triangle or threesided figure is the prime or most simple figure of all rectilineals. For amongst rectilineall figures there is none of two sides: For two right lines cannot inclose a figure. What is meant by a prime figure, was taught at the 11. e. iiij.

And

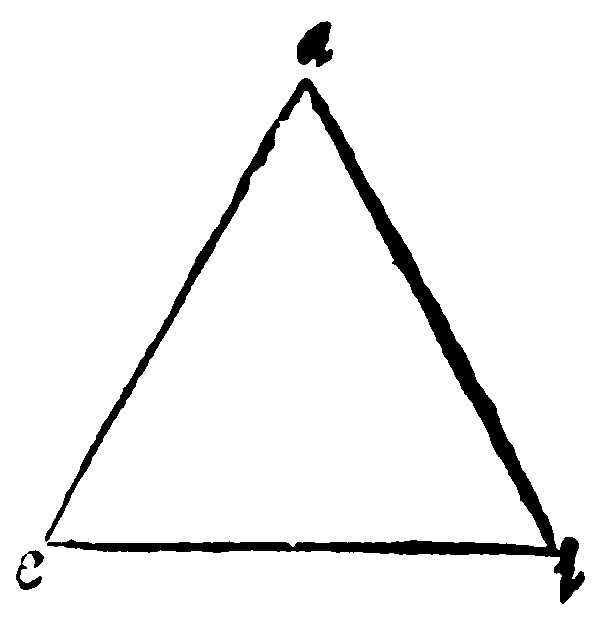
8. If an infinite right line doe cut the angle of a triangle, it doth also cut the base of the same: Vitell. 29. t j.

9. Any two sides of a triangle are greater than the other.

Thus much of the difinition of a triangle; the reason or rate in the sides and angles of a triangle doth follow. The reason of the sides is first.

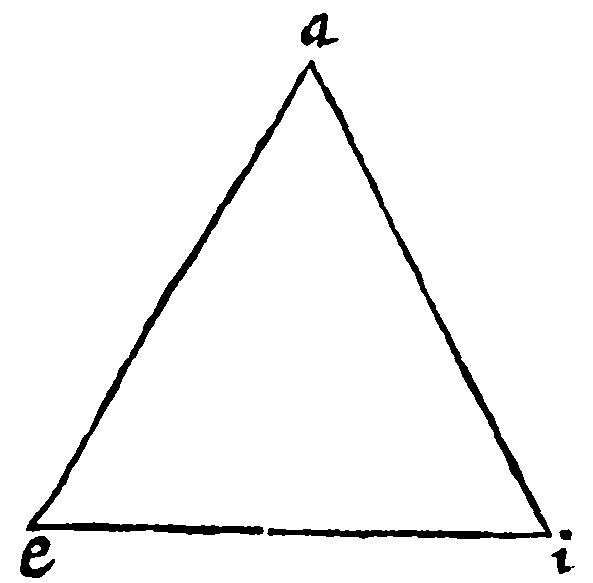
Let the triangle be aei; I say, the side ai, is shorter, than the two sides ae, and ei, because by the 6. e ij, a right line is betweene the same bounds the shortest.

Therefore

10. If of three right lines given, any two of them be greater than the other, and peripheries described upon the ends of the one, at the distances of the other two, shall meete, the rayes from that meeting unto the said ends, shall make a triangle of the lines given.

Let it be desired that a triangle be made of these three lines, aei, given, any two of them being greater than the other: First let there be drawne an infinite right; From this let there be cut off continually three portions, to wit, ou, uy, and ys, equall to ae, and i, the three lines given. Then upon the ends y, and u, at the distances ou, and ys; let two peripheries meet in the point r. The rayes from that meeting unto the said ends, u, and y, shall make the triangle ury: for those rayes shall be equall to the right lines given, by the 10. e v.

And

11. If two equall peripheries, from the ends of a right line given, and at his distance, doe meete, lines drawne from the meeting, unto the said ends, shall make an equilater triangle upon the line given. 1 p. j.

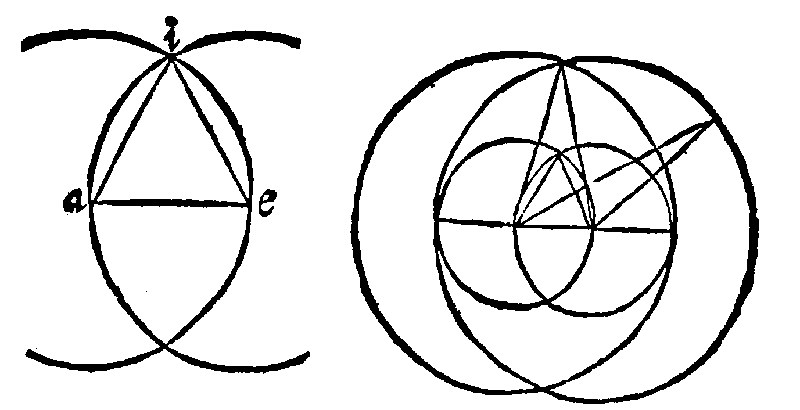
As here upon ae, there is made the equilater triangle, aei; And in like manner may be framed the construction of an equicrurall triangle, by a common ray, unequall unto the line given; and of a scalen or various triangle, by three diverse raies; all which are set out here in this one figure. But these specialls are contained in the generall probleme: neither doe they declare or manifest unto us any new point of Geometry.

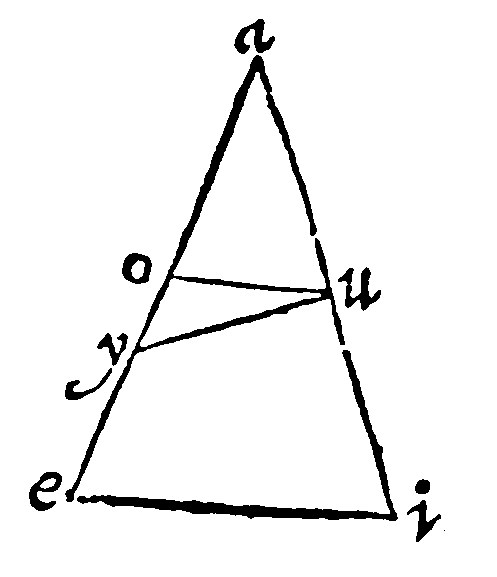
12. If a right line in a triangle be parallell to the base, it doth cut the shankes proportionally: And contrariwise. 2 p vj.

Such therefore was the reason or rate of the sides in one triangle; the proportion of the sides followeth.

As here in the triangle aei, let ou, be parallell to the base; and let a third parallel be understood to be in the toppe a; therefore, by the 28. e. v. the intersegments are proportionall.

The converse is forced out of the antecedent: because otherwise the whole should be lesse than the part. For if ou, be not parallell to the base ei, then yu, is: Here by the grant, and by the antecedent, seeing ao, oe, ay, ye, are proportionall: and the first ao, is lesser than ay, the third: oe, the second must be lesser than ye, the fourth, that is the whole then the part.

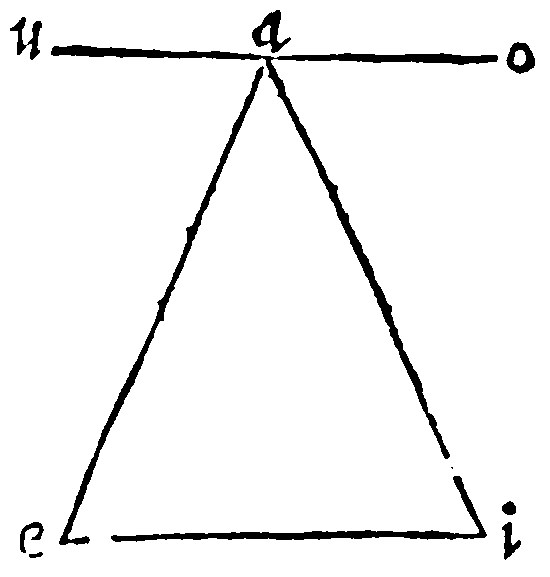
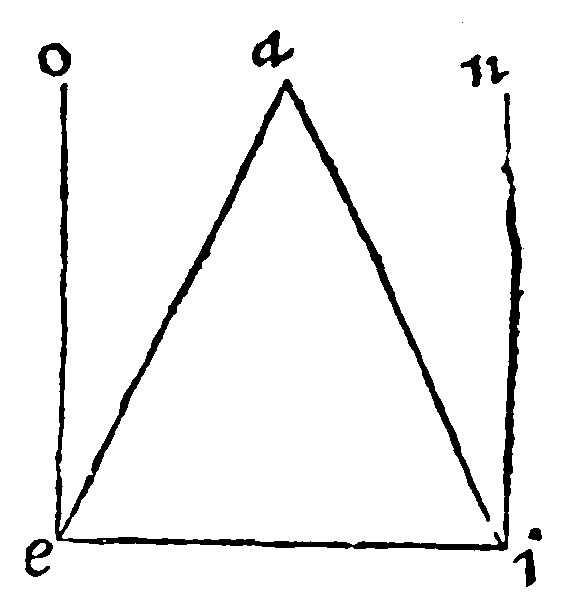
13. The three angles of a triangle, are equall to two right angles. 32. p j.

Hitherto therefore is declared the comparison in the sides of a triangle. Now is declared the reason or rate in the angles, which joyntly taken are equall to two right angles.

The truth of this proposition, saith Proclus, according to common notions, appeareth by two perpendiculars erected upon the ends of the base: for looke how much by the leaning of the inclination, is taken from two right angles at the base, so much is assumed or taken in at the toppe, and so by that requitall the equality of two right angles is made; as in the triangle aei, let, by the 24. e v, ou, be parallell against ie. Here three particular angles, iao, iae, eau, are equall to two right lines; by the 14. e v. But the inner angles are equall to the same three: For first, eai, is equall to it selfe: Then the other two are equall to their alterne angles, by the 24. e v.

Therefore

14. Any two angles of a triangle are lesse than two right angles.

For if three angles be equall to two right angles, then are two lesser than two right angles.

And

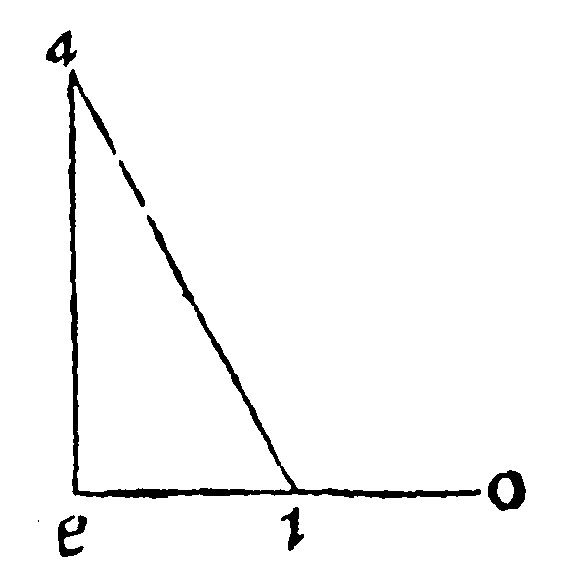
15. The one side of any triangle being continued or drawne out, the outter angle shall be equal to the two inner opposite angles.

This is the rate of the inner angles in one and the same triangle: The rate of the outter with the inner opposite angles doth followe. As in the triangle aei, let the side ei, be continued or drawne out unto o; the two angles on each side aio and aie, are by the 14 e v. equall to two right angles: and the three inner angles, are by the 13. e. equall also to two right angles; take away aie, the common angle, and the outter angle aio, shall be left equall to the other two inner and opposite angles.

Therefore

16. The said outter angle is greater than either of the inner opposite angles. 16. p j.

This is a consectary following necessarily upon the next former consectary.

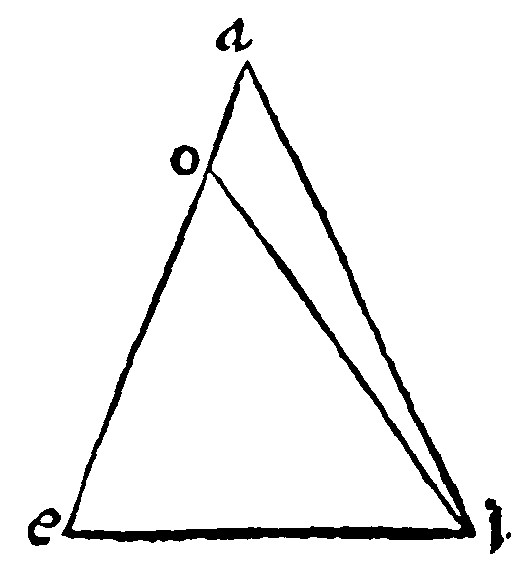
17. If a triangle be equicrurall, the angles at the base are equall: and contrariwise, 5. and 6. p. j.

The antecedent is apparent by the 7. e iij. The converse is apparent by an impossibilitie, which otherwise must needs follow. For if any one shanke be greater than the other, as ae: Then by the 7. e v. let oe, be cut off equall to it: and let oi, be drawne: then by 7. e iij. the base oi, must be equal to the base ae; but the base oi, is lesser than ae. For by the 9. e, ia; and ao, (to which ae, is equall, seeing that oe, is supposed to be equall to the same ai: and ao, is common to both) are greater than the said oi; therefore the same, oi, must be equall to the same ae, and lesser than the same, which is impossible. This was first found out by Thales Milesius.

Therefore

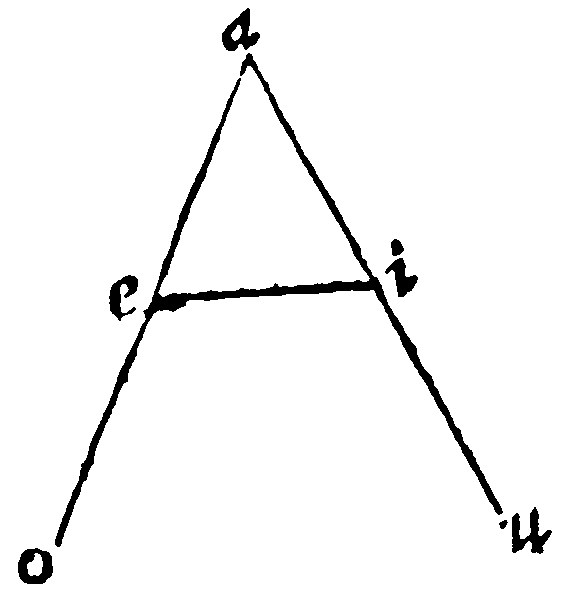
18. If the equall shankes of a triangle be continued or drawne out, the angles under the base shall be equall betweene themselves.

For the angles aei, and ieo: Item aie, and eiu, are equall to two right angles, by the 14. e v. Therefore they are equall betweene themselves: wherefore if you shall take away the inner angles, equall betweene themselves, you shall leave the outter equall one to another.

And

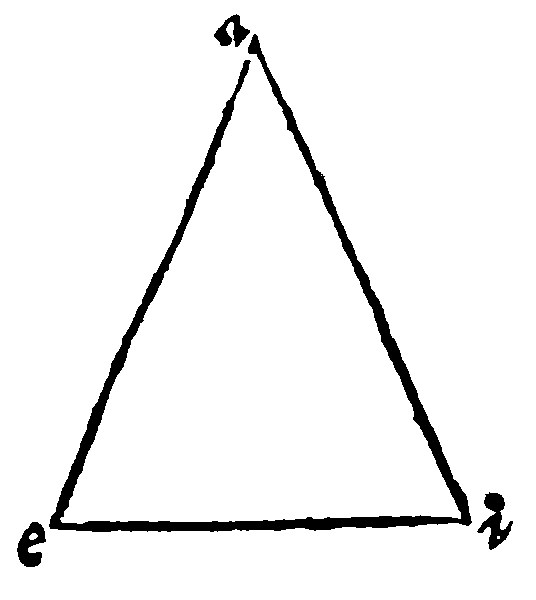
19. If a triangle be an equilater, it is also an equiangle: And contrariwise.

It is a consectary out of the condition of an equicrurall triangle of two, both shankes and angles, as in the example aei, shall be demonstrated.

And

20. The angle of an equilater triangle doth countervaile two third parts of a right angle. Regio. 23. p j.

For seeing that 3. angles are equall to 2. 1. must needs be equall to 2/3.

And

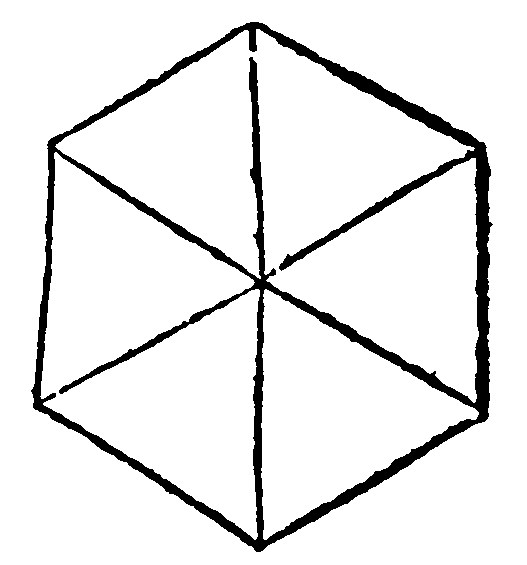
21. Sixe equilater triangles doe fill a place.

As here. For 2/3. of a right angle sixe lines added together doe make 12/3. that is foure right angles; but foure right angles doe fill a place by the 27. e. iiij.

22. The greatest side of a triangle subtendeth the greatest angle; and the greatest angle is subtended of the greatest side. 19. and 18. p j.

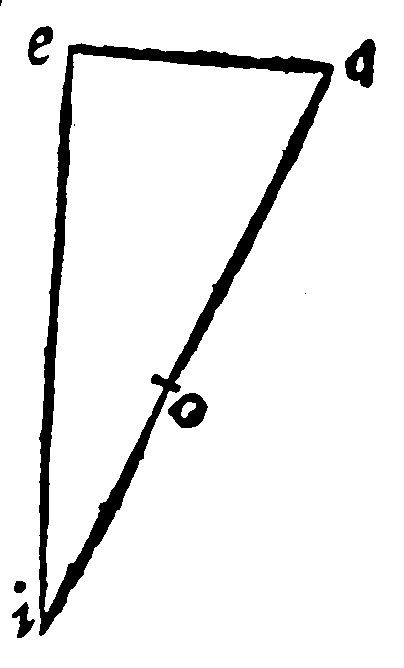
Subtendere, to draw or straine out something under another; and in this place it signifieth nothing else but to make a line or such like, the base of an angle, arch, or such like. And subtendi, is to become or made the base of an angle, arch, of a circle, or such like: As here, let ai, be a greater side than ae, I say the angle at e, shall be greater than that at i. For let there be cut off from ai, a portion equall to ae,; and let that be io: then the angle aei, equicrurall to the angle oie, shall be greater in base, by the grant. Therefore the angle shall be greater, by the 9 e iij.

The converse is manifest by the same figure: As let the angle aei, be greater than the angle aie. Therefore by the same, 9 e iij. it is greater in base. For what is there spoken of angles in generall, are here assumed specially of the angles in a triangle.

23. If a right line in a triangle, doe cut the angle in two equall parts, it shall cut the base according to the reason of the shankes; and contrariwise. 3. p vj.

The mingled proportion of the sides and angles doth now remaine to be handled in the last place.

Let the triangle be aei; and let the angle eai, be cut into two equall parts, by the right line ao: I say, as ea, is unto ai, so eo, is unto oi. For at the angle i, let the parallell iu, by the 24. e v. be erected against ao; and continue or draw out ea, infinitly; and it shall by the 20. e v. cut the same iu, in some place or other. Let it therefore cut it in u. Here, by the 28. e v. as ea, is to au, so is eo, to oi. But au, is equall to ai, by the 17. e. For the angle uia, is equall to the alterne angle oai, by the 21. e v. And by the grant it is equall to oae, his equall: And by the 21. e v. it is equall to the inner angle aui; and by that which is concluded it is equall to uia, his equall. Therefore by the 17. e, au, and ai, are equall. Therefore as ea, is unto ai, so is eo, unto oi.

The Converse likewise is demonstrated in the same figure. For as ea, is to ai; so is eo, to oi: And so is ea, to au, by the 12 e: therefore ai, and au, are equall, Item the angles eao, and oai, are equall to the angles at u, and i, by the 21. e v. which are equall betweene themselves by the 17. e.

Of Geometry, the seventh Booke, Of the comparison of Triangles

1. Equilater triangles are equiangles. 8. p. j.

Thus forre of the Geometry, or affections and reason of one triangle; the comparison of two triangles one with another doth follow. And first of their rate or reason, out of their sides and angles: Whereupon triangles betweene themselves are said to be equilaters and equiangles. First out of the equality of the sides, is drawne also the equalitie of the angles.

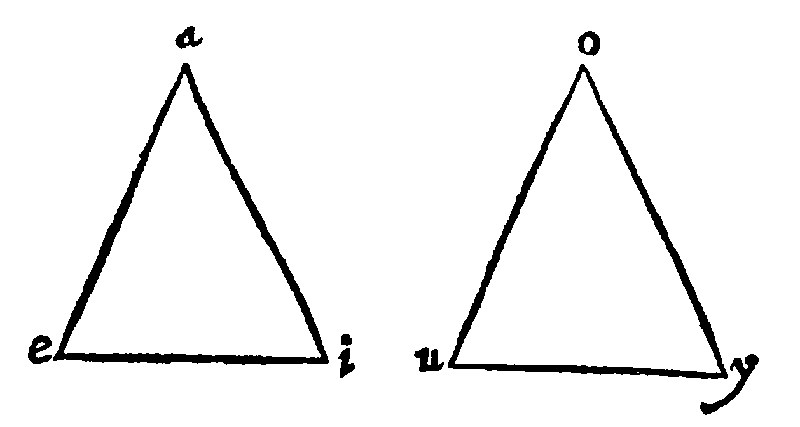
Triangles therefore are here jointly called equilaters, whose sides are severally equall, the first to the first, the second, to the second, the third to the third; although every severall triangle be inequilaterall. Therefore the equality of the sides doth argue the equality of the angles, by the 7. e iij. As here.

2. If two triangles be equall in angles, either the two equicrurals, or two of equall either shanke, or base of two angles, they are equilaters, 4. and 26. p j.

Or thus; If two triangles be equall in their angles, either in two angles contained under equall feet, or in two angles, whose side or base of both is equall, those angles are equilater. H.

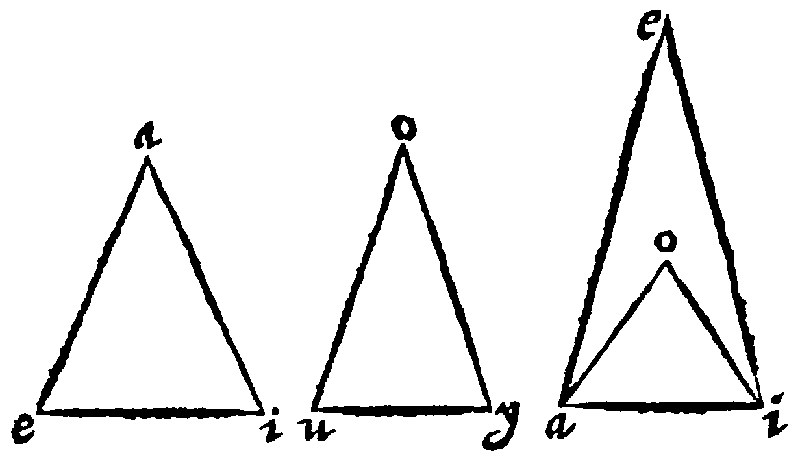
This element hath three parts, or it doth conclude two triangles to be equilaters three wayes. 1. The first part is apparent thus: Let the two triangles be aei, and ouy; because the equall angles at a, and o, are equicrurall, therefore they are equall in base, by the 7. e iij.

2 The second thus: Let the said two triangles aei, and ouy, be equall in two angles a peece, at e, and i, and at u, and y. And let them be equall in the shanke ei, to uy. I say, they are equilaters. For if the side ae, (for examples sake) be greater than the side ou, let es, be cut off equall unto it; and draw the right line is. Here by the antecedent, the triangles sei, and ouy, shall be equiangles, and the angles sie, shall be equall to the angle oyu, to which also the whole angle aie, is equall, by the grant. Therefore the whole and the part are equall, which is impossible. Wherefore the side ae, is not unequall but equall to the side ou: And by the antecedent or former part, the triangles aei, and ouy, being equicrurall, are equall, at the angle of the shanks: Therefore also they are equall in their bases ai, and oy.

3 The third part is thus forced: In the triangles aei, and ouy, let the angles at e, and i, and u, and y, be equall, as afore: And ae, the base of the angle at i, be equall to ou, the base of angle at y: I say that the two triangles given are equilaters. For if the side ei, be greater than the side uy, let es, be cut off equall to it, and draw the right line as. Therefore by the antecedent, the two triangles, aes, and ouy, equall in the angle of their equall shankes are equiangle: And the angle ase, is equall to the angle oyu, which is equall by the grant unto the angle aie. Therefore ase, is equall to aie, the outter to the inner, contrary to the 15. e. vj. Therefore the base ei, is not unequall to the base uy, but equall. And therefore as above was said, the two triangles aei, and ouy, equall in the angle of their equall shankes, are equilaters.

3. Triangles are equall in their three angles.

The reason is, because the three angles in any triangle are equall to two right angles, by the 13. e vj. As here, the greatest triangle, all his corners joyntly taken, is equall to the least.

And yet notwithstanding it is not therefore to be thought to be equiangle to it: For Triangles are then equiangles, when the severall angles of the one, are equall to the severall angles of the other: Not when all joyntly are equall to all.

Therefore

4. If two angles of two triangles given be equall, the other also are equall.

All the three angles, are equall betweene themselves, by the 3 e. Therefore if from equall you take away equall, those which shall remaine shall be equall.

5. If a right triangle equicrurall to a triangle be greater in base, it is greater in angle: And contrariwise. 25. and 24. p j.

Thus farre of the reason or rate of equality, in the sides and angles of triangles: The reason of inequality, taken out of the common and generall inequality of angles, doth follow. The first is manifest, by the 9. e iij. as here thou seest in aei and ouy.

6. If a triangle placed upon the same base, with another triangle, be lesser in the inner shankes, it is greater in the angle of the shankes.

This is a consectary drawne also out of the 10 e iij. As here in the triangle aei, and aoi, within it and upon the same base. Or thus: If a triangle placed upon the same base with another triangle, be lesse then the other triangle, in regard of his feet, (those feete being conteined within the feete of the other triangle) in regard of the angle conteined under those feete, it is greater: H.

7. Triangles of equall heighth, are one to another as their bases are one to another.

Thus farre of the Reason or rate of triangles: The proportion of triangles doth follow; And first of a right line with the bases. It is a consectary out of the 16 e iiij.

Therefore

8. Upon an equall base, they are equall.

This was a generall consectary at the 16. e iiij: From whence Archimedes concluded, If a triangle of equall heighth with many other triangles, have his base equall to the bases of them all, it is equall to them all: as here thou seest aei to be equall to the triangles aeo, uoy, syr, lrm, nmi. Here hence also thou mayst conclude, that Equilater triangles are equall: Because they are of equall heighth, and upon the same base.

And

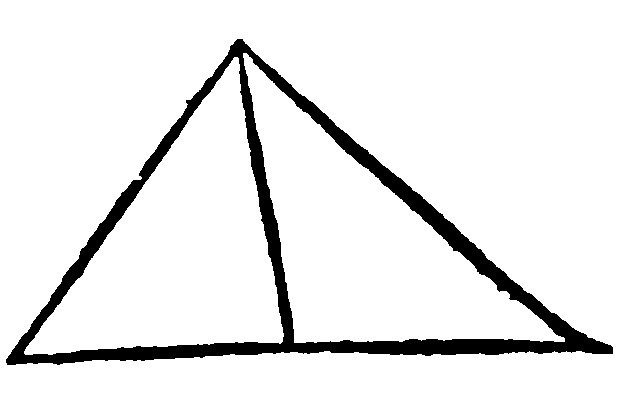
9. If a right line drawne from the toppe of a triangle, doe cut the base into two equall parts, it doth also cut the triangle into two equall parts: and it is the diameter of the triangle.

As here thou seest: For the bisegments, or two equall portions thus cut are two triangles of equall heighth that is to say, they have one toppe common to both, within the same parallels) and upon equall bases: Therefore they are equall: And that right line shall be the diameter of the triangle, by the 5 e iiij, because it passeth by the center.

10. If a right line be drawne from the toppe of a triangle, unto a point given in the base (so it be not in the middest of it) and a parallell be drawne from the middest of the base unto the side, a right line drawne from the toppe of the sayd parallell unto the sayd point, shall cut the triangle into two equall parts.

Let the triangle given be aei: And let ao, cut the base ei, in o unequally: And let uy be parallell from u, the middest of the base, unto the sayd ao. I say that yo shall divide the triangle into two equall portions. For let au be knit together with a right line: That line, by the 9 e, shall divide the triangle into two equall parts. Now the two triangles ayu, and you, are equall by the 8 e; because they are of equall height, and upon the same base.

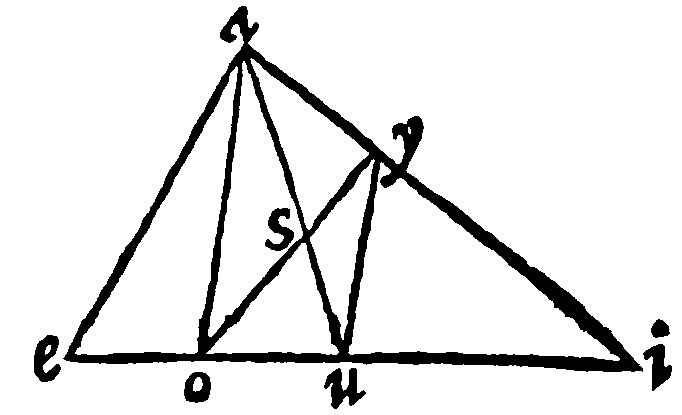
Take away ysu, the common triangle; And you shall leave asy, and osu, equall betweene themselves: The common right lined figure ysui, let it be added to both the sayd equall triangles: And then oyi, shall be equall to aui, the halfe part; And therefore aeoy, the other right lined figure, shall be the halfe of the triangle given.

11. If equiangled triangles be reciprocall in the shankes of the equall angle, they are equall: And contrariwise. 15. p. vj. Or thus, as the learned Mr. Brigges hath conceived it: If two triangles, having one angle, are reciprocall, &c.

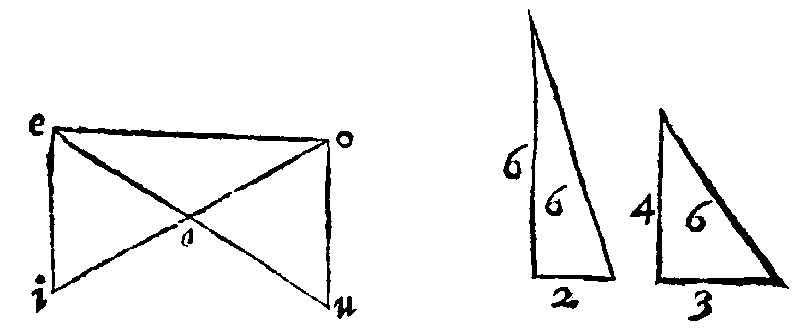
Direct proportion in triangles, is such as hath in the former beene taught: Reciprocall proportion followeth. It is a consectary drawne out of the 18 e iiij; which is manifest, as oft as the equall angle is a right angle: For then those shankes, [comprehending the equall angles,] are the heights and the bases; As here thou seest in the severed triangles. Notwithstanding in obliquangle triangles, although the shankes are not the heights, the cause of the truth hereof is the same. Yet if any man shall desire a demonstration of it, it is thus: Let therefore the diagramme or figure bee in the triangles aei, and aou: And the angles oau, and eai, let them be equall: And as ua is to ae, so let ia be unto ao: I say that the triangles aou, and eai, are equall. For eo being knit together with a right line, uao is unto oae, as ua is unto ae, by the 7 e: And ia, unto ao, by the grant, is as eai is unto eao. Therefore uao, and eai, are unto eao proportionall: And therefore they are equall one to another.