The Way To Geometry

The converse, is concluded by the same sorites, but by saying all backward. For ua unto ae is, as uao is unto oae, by the 7 e: And as eai, by the grant: Because they are equall: And as ia is unto ao, by the same, Wherefore ua is unto ae, as ia is unto ao.

12. If two triangles be equiangles, they are proportionall in shankes: And contrariwise: 4 and 5. p. vj.

The comparison both of the rate and proportion of triangles hath in the former beene taught: Their similitude remaineth for the last place. Which similitude of theirs consisteth indeed of the reason, or rate of their angles and proportion of the shankes. Therefore for just cause was the reason of the angles set first: Because from thence not onely their reason, but also their latter proportion is gathered. Let aei and iou, be two triangles equiangled: And let them be set upon the same line eiu, meeting or touching one another in the common point i. Then, seeing that the angles at e and i, are granted to bee equall, the lines oi, and ae, are parallel, by the 21 e v. Therefore by the 22 e v uo and ea, being continued, shall meete. Item, The right lines ai, and yu, by the 21 e v, are parallel, because the angle aie is equall to oui, the inner opposite to it. Therefore seeing that ai is parallell to the base yu, by the 21 e v, ea shall be to ay, that is, by the 26 e v, to io, as ei is to iu: And alternly, or crosse wayes, ea shall be to ei, as io is to iu. This is the first proportion. Item, seeing that io is parallell to the base ye; yo, that is, by the 26 e v, ai shall bee unto ou, as ei, is unto iu: And crosse wise, as ai is unto ie, so is ou unto ui. This is the second proposition. Lastly, equiordinately: ae is to ai, as oi is to ou: wherefore if triangles be equiangled, they are proportional in shankes.

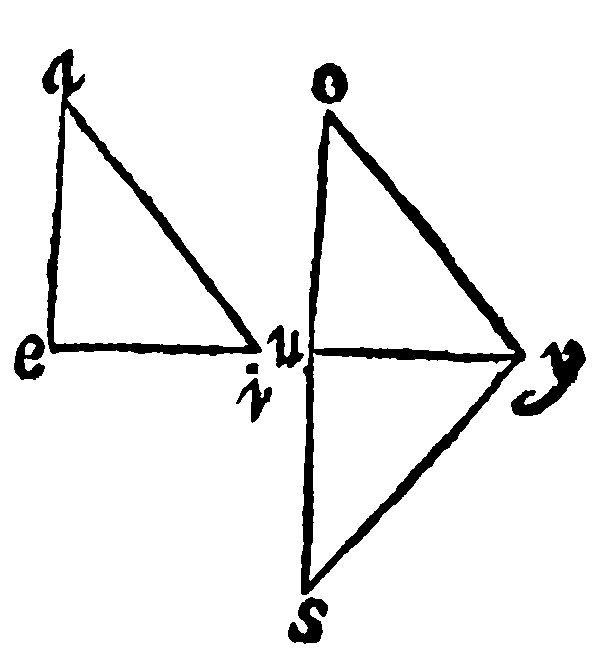
This converse is thus demonstrated. Let there be two triangles aei, and ouy, proportionall in shankes: And as ae is to ei; so let ou, be to uy: And as ai is to ie; so let oy bee to yu. Then at the points u and y, let angles be made by the 11 e iij. equall to the angles at e and i, and let the triangle uys, be made: for the other angles at a and s, shall be equall by the 4 e. And the triangle yus, shall be equiangled to the assigned aei. And by the antecedent, it shall be proportionall to it in shankes. Thus are two triangles ouy, by the grant; and uys, by the construction, proportionall in shanks to the same triangle aei: And as ae, is to ei, so is ou, to uy; so is su, to uy. Therefore seeing ou and su, are proportionall to the same yu, they are equall; Item, as ai is to ie: so is oy unto yu: so also is sy unto yu. Therefore oy and sy, seeing they are proportionall to the same yu, are equall. (yu is the common side.) The triangle therefore ouy, is equilater unto the triangle syu. And by the 1 e, it is to it equiangle: And therefore it is equiangled to the triangle aei, which was to be prooved. This was generally before taught at the 20 e iiij, of homologall sides subtending equall angles.

Therefore,

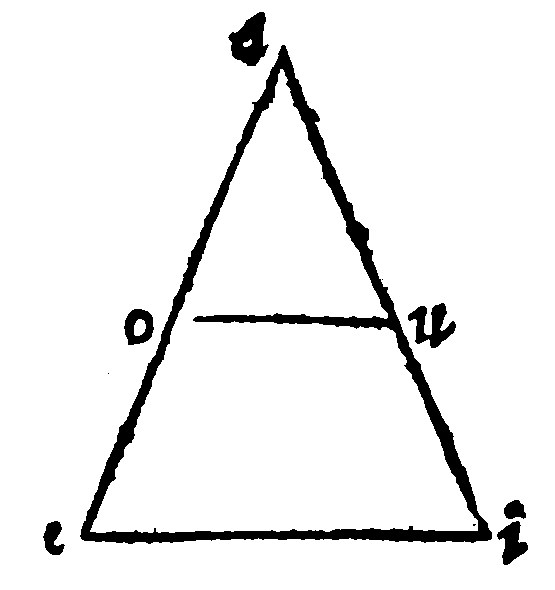
13. If a right line in a triangle be parallell to the base, it doth cut off from it a triangle equiangle to the whole, but lesse in base.

As in the triangle aei, the right line ou, doth cut off the triangle aou, equiangle, by the 21 e v, to the whole aei; But the base ou, is lesse than the base ei, as appeareth by the 21 e, and by the alternation of the sides.

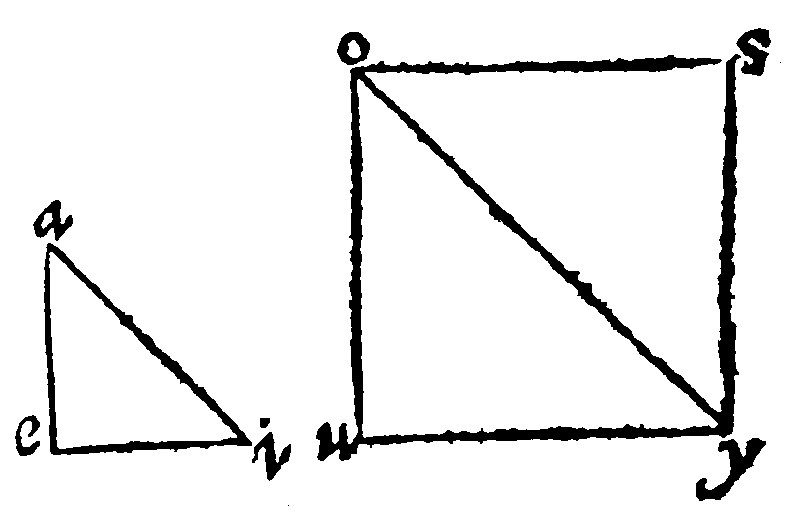
14. If two trangles be proportionall in the shankes of the equall angle, they are equiangles: 6 p vj.

Let therefore the triangles given be aei, and ouy, equall in their angles a and o: And in their shankes let ea, be unto ai, as ou is to oy: And by the 11 e iij, let the angles soy, and oys, be equall to the angles eai, and eia: The other at s and e, shall be equall, by the 4 e. Here thou seest that the triangle aei, is equiangle unto oys. Now, by the 12 e. as ea is to ai: so is so to oy: and therefore, by the grant, so is uo to oy. Therefore seeing that uo, and os, are proportionall to oy, they are both equall. Lastly, if the common shanke oy bee added to both the shankes ou, and oy, are equall to the shankes so and oy. [But by the construction the angles oys and aie are equall. And, by the 4 e, the other at s and e are equall. Therefore the first triangle aei, is made equiangled to the third. Now seeing the second triangle uoy is to the third soy, equall in the shanks of the equall angle, it is to the same equilater, and by the 1 e, equiangled: Shon.] Wherefore the second triangle ouy shall likewise be equiangled to osy, the third: And therefore if two triangles proportionall in shankes be equall in the angle of their shankes, they are equiangles.

15. If triangles proportionall in shankes, and alternly parallell, doe make an angle betweene them, their bases are but one right line continued. 32 p. vj.

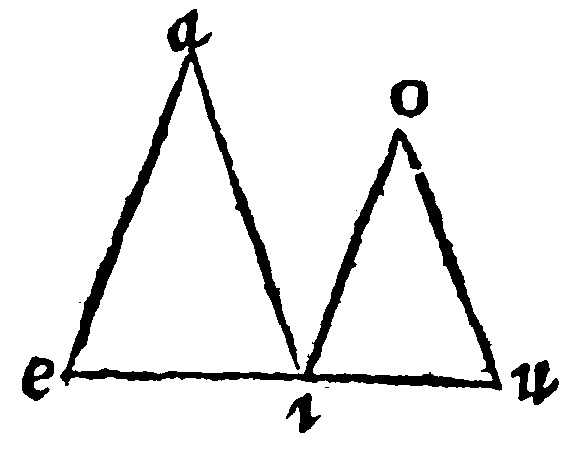
Or thus: If being proportionall in their feet, and alternately parallels, they make an angle in the midst betweene them, they have their bases continued in a right line: H.

The cause is out of the 14 e v. For they shall make on each side, with the falling line ai, two angles equall to two right angles.

Let the triangles aei and oiu, be proportionall in shanks: As ae is to ai, so let io be to ou: And let ea bee parallel to io: And ai to ou: Item, let them make the angle aio, betweene them, to wit, betweene their middle shankes ai, and oi, I say their bases ei, and iu, are but one right line continued. For seeing that by the grant ae, and oi, are parallels: Item ai and uo, the right line ai and oi, shall make, by the 21 e v, the angles at a, and o, equall to the alterne angle aio: And therefore they are equall betweene themselves: And then, by the 14 e, the triangles given are equiangles: Therefore the angle oui, is equall to the angle aie: Wherfore the three angles oiu, oia, and aie, by the 3 e, are equall to the three angles of the triangle eai, which are equall by the 13 e vj. Unto two right angles: And therefore they themselves also are equall to two right angles. Wherefore, by the 14 e v, ei, and iu, are one right line continued.

16. If two triangles have one angle equall, another proportionall in shankes, the third homogeneall, they are equiangles. 7. p. vj.

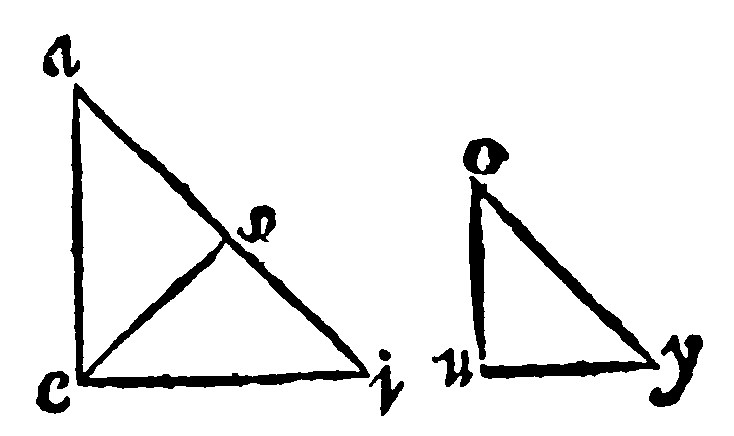
Let aei, and ouy, the triangles given be equall in their angles a, and o: and proportionall in the shankes of the angles e, and u: and their other angles, at i, and y, homogeneall, that is, let them be both, either acute, or obtuse, or right angles. But first let them be acute, I say, the other at e, & u, are equall. Otherwise let aes, by the 11 e iij. be made equall to the same ouy; Then have you them by the 4 e, equiangles; and the angles ase, shall be equall to the angle oyu; and both are acute angles: and by the 12. e, aes, and ouy, are proportionall in sides: and as ae, is to es; so shall ou, be to uy, that is, by the grant, so shall ae, be to ei. Therefore because the same ea, hath unto two, to wit, es, and ei, the same reason, the said es, and ei, are equall one to another: And therefore, by the 17. e. vj. the angles at the base in s and i, are equall. Therefore both of them are acute angles: And in like manner ase, is an acute angle, contrary to the 14. e v. The same will fall out altogether like to both the other, being either obtuse or right angles. The last part of a right angle is manifest by the 4 e of this Booke.

Of Geometry the eight Booke, of the diverse kindes of Triangles

1. A triangle is either right angled, or obliquangled.

The division of a triangle, taken from the angles, out of their common differences, I meane, doth now follow. But here first a speciall division, and that of great moment, as hereafter shall be in quadrangles and prismes.

2. A right angled triangle is that which hath one right angle: An obliquangled is that which hath none. 27. d j.

A right angled triangle in Geometry is of speciall use and force; and of the best Mathematicians it is called Magister matheseos, the master of the Mathematickes.

Therefore

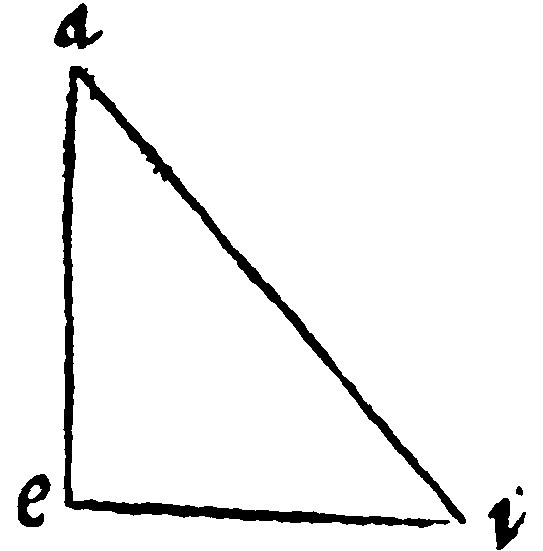
3. If two perpendicular lines be knit together, they shall make a right angled triangle.

As here in aei. This construction and manner of making of a right angled triangle, is drawne out of the definition of a right angle. For right lines perpendicular are the makers of a right angle, as is manifest by the 13. e iij.

4. If the angle of a triangle at the base, be a right angle, a perpendicular from the toppe shall be the other shanke: [and contrariwise Schon.]

As is manifest in the same example.

5. If a right angled triangle be equicrurall, each of the angles at the base is the halfe of a right angle: And contrariwise.

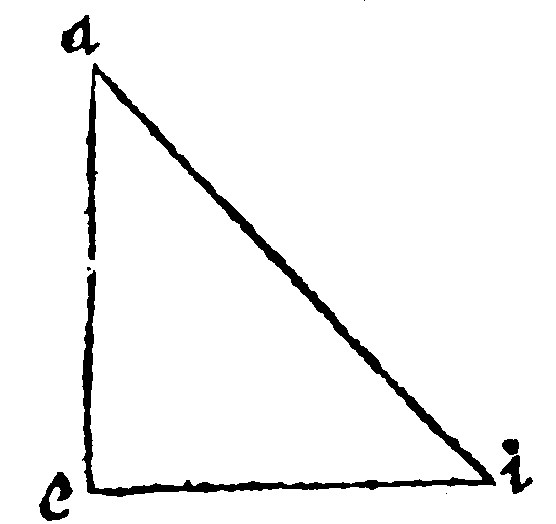
As in the triangle aei: For they are both equall to one right angle, by the 13. e. vj. And betweene themselves, by the 17. e. vj.

Therefore

6. If one angle of a triangle be equall to the other two, it is a right angle [And contrariwise Schon.]

Because it is equall to the halfe of two right angles, by the 13. e vj.

And

7. If a right line from the toppe of a triangle cutting the base into two equall parts be equall to the bisegment, or halfe of the base, the angle at the toppe is a right angle: [And contrariwise Schon.]

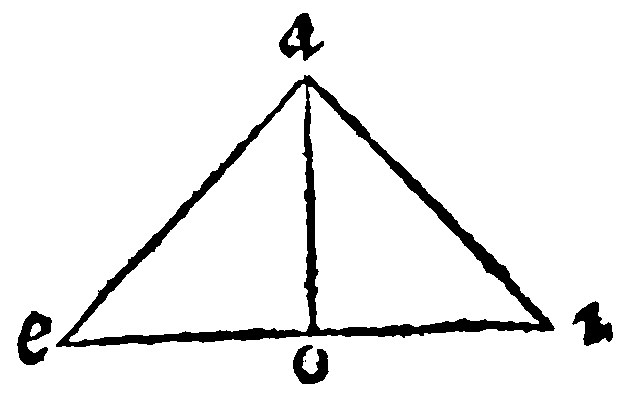
As in the triangle aei, the right line ao, cutting the base ei, in o, into two equall parts, is equall to eo, or oi, the halfe of the base maketh two equicrural triangles; and the severall angles at the top equall to the angles at the ends, viz. e, and i, by the 17. e. vj. Therefore the angle at the toppe is equall to the other two: wherefore by the 6 e, it is a right angle.

8. A perpendicular in a triangle from the right angle to the base, doth cut it into two triangles, like unto the whole and betweene themselves, 8. p vj. [And contrariwise Schon.]

As in the triangle aei, the perpendicular ao, doth cut the triangles aoe, and aoi, like unto the whole aei, because they are equiangles to it; seeing that the right angle on each side is one, and another common in i, and e: Therefore the other is equall to the remainder, by 4. e vij. Wherefore the particular triangles are equiangles to the whole: As proportionall in the shankes of the equall angles, by the 12. e vij. But that they are like betweene themselves it is manifest by the 22. e iiij.

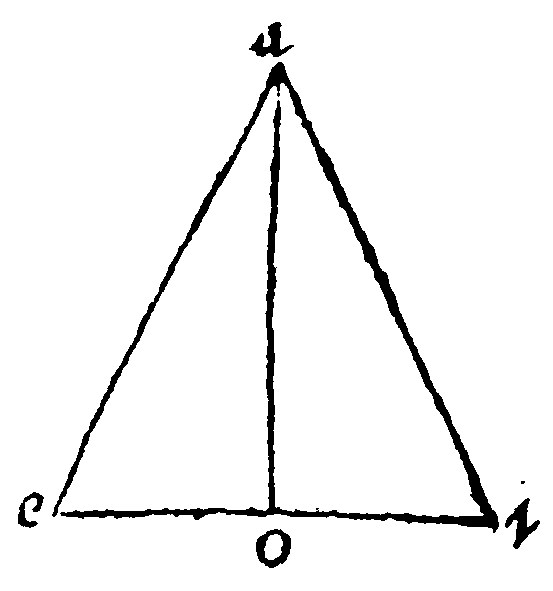
Therefore

9. The perpendicular is the meane proportionall betweene the segments or portions of the base.

As in the said example, as io, is to oa: so is oa, to oe, because the shankes of equall angles are proportionall, by the 8. e. From hence was Platoes Mesographus invented.

And

10. Either of the shankes is proportionall betweene the base, and the segment of the base next adjoyning.

For as ei, is unto ia, in the whole triangle, so is ai, to io, in the greater. For so they are homologall sides, which doe subtend equall angles, by the 23. e. iiij. Item, as ie, is to ea; in the whole triangle, so is ae, to eo, in the lesser triangle.

Either of the shankes is proportionall betweene the summe, and the difference of the base and the other shanke. And contrariwise. If one side be proportionall betweene the summe and the difference of the others, the triangle given is a rectangle. M. H. Brigges.

This is a consectary arising likewise out of the 4 e. of very great use.

In the triangle ead, the shanke ad, 12. is the meane proportionall betweene bd, 18. (the summe of the base ae, 13. and the shanke ed, 5.) and 8. the difference of the said base and shanke: For if thou shalt draw the right lines ba, and ac, the angle bac, shall be by the 6. e, a rectangle; (because it is equall to the angles at b, and c, seeing that the triangles bea, and eac, are equicrurall.) And by the 9 e, bd, da, and dc, are continually proportionall.

If a quadrate of a number, given for the first shanke, be divided of another, the halfe of the difference of the divisour, and quotient shall be the other shanke, and the halfe of the summe shall be the base. Or thus, The side of divided number doubled, and the difference of the divisour and quotient, shall be the two shankes, and the summe of them shall be the base.

Let the number given for the first shanke be 4. And let 8. divide 16. the quadrate of 4. by 2. The halfe of 8 – 2, that is 3. shall be the other shanke: And the halfe of 8 + 2, that is 5. shall be the base.

Therefore

If any one number shall divide the quadrate of another, the side of the divided, and the halfe of the difference of the divisour and the quotient, shall be the two shankes of a rectangled triangle, and the halfe of the summe of them shall be the base thereof.

Let the two numbers given be 4. and 6. The square of 6. let it be 36. and the quotient of 36. by 4. be 9: And the side is 6. for the one shanke. Now 9 – 4. that is, 5. is the difference of the divisour and quotient, whose halfe 2.½, is the other shanke. And 9 + 4. that is 13. is the summe the said devisour and quotient, whose halfe 6.½, is the base.

Againe let 4. and 8. be given. The quadrate of 8. is 64. And the quotient of 64 is 16. and the side of 64. is 8. for the one shanke. The halfe 16 – 4. that is 6. is the other shanke. And the halfe of 16 + 4. that is 10, is the base.

11. If the base of a triangle doe subtend a right-angle, the rectilineall fitted to it, shall be equall to the like rectilinealls in like manner fitted to the shankes thereof: And contrariwise, out of the 31. p. vj.

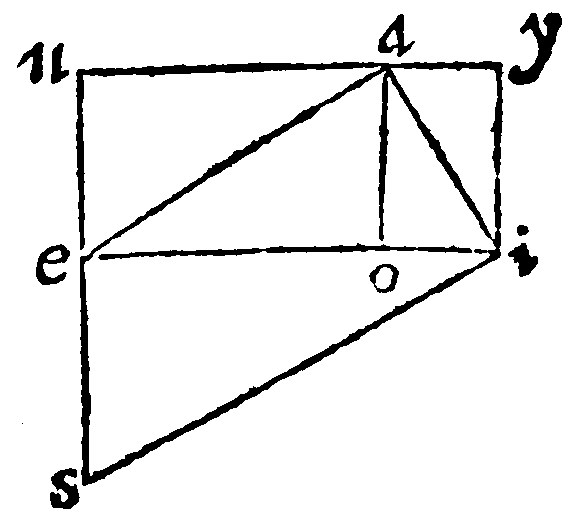
Or thus: If the base of a triangle doe subtend a right angle, the right lined figure made upon the base, is equall to the right lined figures like, and in like manner situate upon the feete: H.

Let the right angled triangle be aei: and let there be also the triangles eau, and aiy, and to them upon the base of the said right angle, by the 23 e iiij. let the triangle ies, be made like, and in like manner situate. I say, that eis, is equall joyntly to eau, and aiy. Let ao, a perpendicular fall from the right angle a, to the base ei: This by the ioe, doth yeeld us twise three proportionals, to wit, ie, ea, eo: Item, ei, ia, io: Therefore, by the 25. e. iiij, as ie, is to eo: so is the triangle ies, to the triangle eau; And as ei, is to oi, so is the triangle eis, to the triangle aiy: But ei, is equall to eo, and oi, the whole, to wit, to his parts. Wherefore by the second composition in Arithmeticke (9. c. ij.) the triangle eis, is equall to the triangles eau, and iay.

The Converse is thus proved: Let the triangle be aei: And let the perpendicular eo, be erected upon ae, equall to ei: And draw a right line from o to a: Here by the former, the rectilinealls situate at oe, and ea, that is by the construction, at ae, and ie, are equall to the rightilineall at ao, made alike and situate alike: And by the graunt they are equall, to the rectilineall at ai, made alike and situated alike. Therefore seeing the like rectilineals at ao, and ai, are equall; they have by the 20 e iiij, their homologall sides equall: And the two triangles are equiliters: And by the 1 e vij, equiangles. But aeo, is a right angle, by the construction: And aei, is proved to be equall to the same aeo: Therefore, by the 13 e v. aei, also is a right angle.

12. An obliquangled triangle is either Obtusangled or Acutangled.

The division of an obliquangled triangle is taken from the speciall differences of an oblique angle. For at the 15 e iij, we were taught that an oblique angle was either obtuse or acute: Therefore an obliquangled triangle is an obtuseangle, and an Acutangle.

13. An obtusangle is that triangle which hath one blunt corner. 28.d i.

There can be but one right angle in a triangle, by the 2 e. Therefore also in it there can be but one blunt angle.

Therefore

14. If the obtuse or blunt angle be at the base of the triangle given, a perpendicular drawne from the toppe of the triangle, shall fall without the figure: And contrarywise.

As here in aei, the perpendicular io, falleth without: This is manifest by the 4 e.

And

15. If one angle of a triangle be greater than both the other two, it is an obtuse angle: And contrariwise.

This is plaine by the 6 e.

And

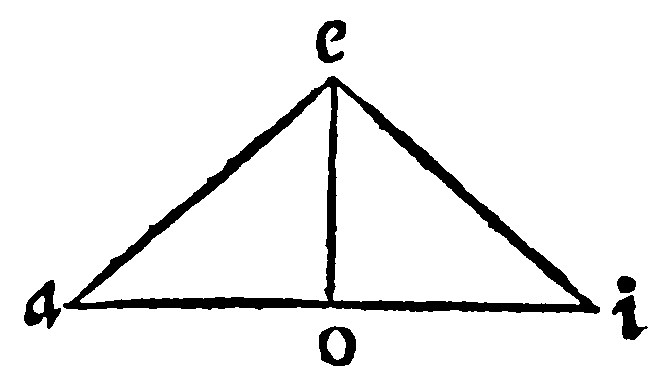
16. If a right line drawne from the toppe of the triangle cutting the base into two equall parts, be lesse than one of those halfes, the angle at the toppe is a blunt-angle. And contrariwise.

As in aei, the perpendicular eo, cutting the base ai into two equall parts ao, and oi: And the said eo is lesse than either ao, or oi: Therefore the angle aei, is a blunt angle by the 7 e.

17. An acutangled triangle is that which hath all the angles acute. 29 d j.

Therefore

18. A perpendicular drawne from the top falleth within the figure: And contrariwise.

As in aei, the perpendicular ao falleth within as is plaine by the 4 e.

And

19. If any one angle of triangle be lesse then the other two, it is acute: And contrariwise.

As is manifest by the 6 e.

And

20. If a right line drawne from the toppe of the triangle; cutting the base into two equall parts, be greater than either of those portions, the angle at the toppe is an acute angle: And contrariwise.

As in aei, let ao cutting the base ei into two equall parts, be greater than any one of those parts, the angle at the toppe is an acuteangle, as appeareth by the 7 e.

The ninth Booke, of P. Ramus Geometry, which intreateth of the measuring of right lines by like right-angled triangles

The Geometry of like right-angled triangles, amongst many other uses that it hath, it doth especially afford us the geodæsy or measuring of right lines: And that mastery, which before (at the 2 e viij) attributed the right angled triangles, shall here be found to be a true mastery indeed. For it shall containe the geodesy of right lines; and afterward the geodesy of plaines and solides, by the measuring of their sides, which are right lines.

1. For the measuring of right lines; we will use the Iacobs staffe, which is a squire of unequall shankes.

Radius, commonly called Baculus Iacob, Iacobs staffe, as if it had been long since invented and practised by that holy Patriarke, is a very auncient instrument, and of all other Geometricall instruments, commonly used, the best and fittest for this use. Archimedes in his book of the Number of the sand, seemeth to mention some such thing: And Hipparchus, with an instrument not much unlike this, boldly attempted an haynous matter in the sight of God, as Pliny thinketh, namely to deliver unto posterity the number of the starres, and to assigne or fixe them in their true places by the Norma, the squire or Iacobs staffe. And indeed true it is that the Radius is not onely used for the measuring of the earth and land: But especially for the defining or limiting of the starres in their places and order: And for the describing and setting out of all the regions and waies of the heavenly city. Yea and Virgill the famous Poet, in his 3 Ecloge, Ecquis fuit alter, Descripsit radio totum, qui gentibus orbem? and againe afterward in the 6 of his Eneiades, hath noted both these uses. Cœliquè meatus. Describent radio & surgentia sidera dicent. Long after this the Iewes and Arabians, as Rabbi Levi; But in these latter daies, the Germaines especially, as Regiomontanus; Werner, Schoner, and Appian have grac'd it: But above all other the learned Gemma Phrisius in a severall worke of that argument onely, hath illustrated and taught the use of it plainely and fully.

The Iacobs staffe therefore according to his owne, and those Geometricall parts, shall here be described (The astronomicall distribution wee reserve to his time and place.) And that done, the use of it shall be shewed in the measuring of lines.

This instrument, at the discretion of the measurer may be greater or lesser. For the quantity of the same can no otherwayes be determined.

2. The shankes of the staffe are the Index and the Transome.