The Way To Geometry

Therefore,

13. The number of a rationall figure, is called a Figurate number: And the numbers of which it is made, the Sides of the figurate.

As if a Right angled parallelogramme be comprehended of the base foure, and the height three, the Rationall made shall be 12. which wee here call the figurate: and 4. and 3. of which it was made, we name sides.

14. Isoperimetrall figures, are figures of equall perimeter.

This is nothing else but an interpretation of the Greeke word; So a triangle of 16. foote about, is a isoperimeter to a triangle 16. foote about, to a quadrate 16. foote about, and to a circle 16. foote about.

15. Of isoperimetralls homogenealls that which is most ordinate, is greatest: Of ordinate isoperimetralls heterogenealls, that is greatest, which hath most bounds.

So an equilater triangle shall bee greater then an isoperimeter inequilater triangle; and an equicrurall, greater then an unequicrurall: so in quadrangles, the quadrate is greater then that which is not a quadrate: so an oblong more ordinate, is greater then an oblong lesse ordinate. So of those figures which are heterogeneall ordinates, the quadrate is greater then the Triangle: And the Circle, then the Quadrate.

16. If prime figures be of equall height, they are in reason one unto another, as their bases are: And contrariwise.

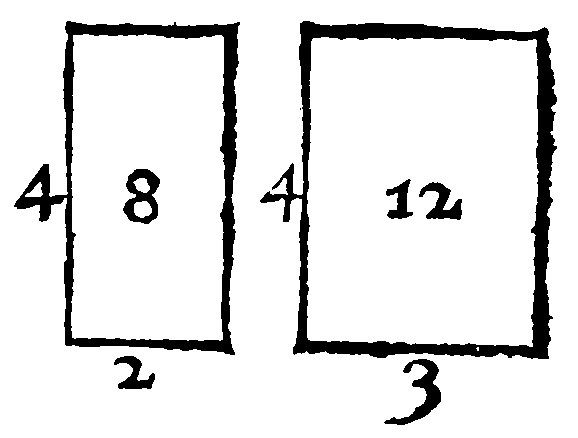
The proportion of first figures is here twofold; the first is direct in those which are of equall height. In Arithmeticke we learned; That if one number doe multiply many numbers, the products shall be proportionall unto the numbers, multiplyed. From hence in rationall figures the content of those which are of equall height is to bee expressed by a number. As in two right angled parallelogrammes, let 4. the same height, multiply 2. and 3. the bases: The products 8. and 12. the parallelogrammes made, are directly proportionall unto the bases 2. and 3. Therefore as 2. is unto 3. so is 8. unto 12. The same shall afterward appeare in right Prismes and Cylinders. In plaines, Parallelogramms are the doubles of triangles: In solids, Prismes are the triples of pyramides: Cylinders, the triples of Cones. The converse of this element is plaine out of the former also: First figures if they be in reason one to another as their bases are, then are they of equall height, to witt when their products are proportionall unto the multiplyed, the same number did multiply them.

Therefore,

17. If prime figures of equall heighth have also equall bases, they are equall.

[The reason is, because then those two figures compared, have equall sides, which doe make them equall betweene themselves; For the parts of the one applyed or laid unto the parts of the other, doe fill an equall place, as was taught at the 10. e. j. Sn.] So Triangles, so Parallelogrammes, and so other figures proposed are equalled upon an equall base.

18. If prime figures be reciprocall in base and height, they are equall: And contrariwise.

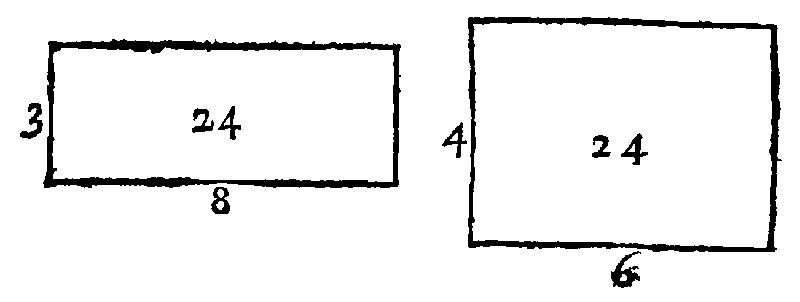
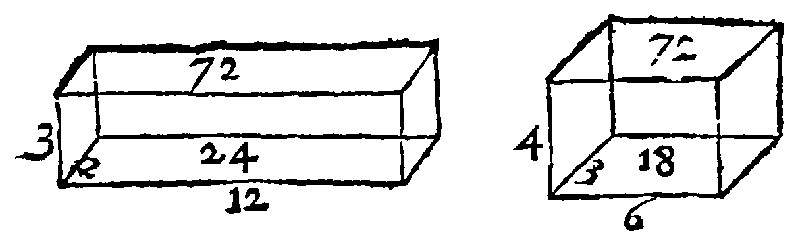
The second kind of proportion of first figures is reciprocall. This kinde of proportion rationall and expressible by a number, is not to be had in first figures themselves: but in those that are equally manifold to them, as was taught even now in direct proportion: As for example, Let these two right angled parallelogrammes, unequall in bases and heighths 3, 8, 4, 6, be as heere thou seest: The proportion reciprocall is thus, As 3 the base of the one, is unto 4, the base of the other: so is 6. the height of the one is to 8. the height of the other: And the parallelogrammes are equall, viz. 24. and 24. Againe, let two solids of unequall bases & heights (for here also the base is taken for the length and heighth) be 12, 2, 3, 6, 3, 4. The solids themselves shall be 72. and 72, as here thou seest; and the proportion of the bases and heights likewise is reciprocall: For as 24, is unto 18, so is 4, unto 3. The cause is out of the golden rule of proportion in Arithmeticke: Because twice two sides are proportionall: Therefore the plots made of them shall be equall. And againe, by the same rule, because the plots are equall: Therefore the bounds are proportionall; which is the converse of this present element.

19. Like figures are equiangled figures, and proportionall in the shankes of the equall angles.

First like figures are defined, then are they compared one with another, similitude of figures is not onely of prime figures, and of such as are compounded of prime figures, but generally of all other whatsoever. This similitude consisteth in two things, to witt in the equality of their angles, and proportion of their shankes.

Therefore,

20. Like figures have answerable bounds subtended against their equall angles: and equall if they themselves be equall.

Or thus, They have their termes subtended to the equall angles correspondently proportionall: And equall if the figures themselves be equall; H. This is a consectary out of the former definition.

And

21. Like figures are situate alike, when the proportionall bounds doe answer one another in like situation.

The second consectary is of situation and place. And this like situation is then said to be when the upper parts of the one figure doe agree with the upper parts of the other, the lower, with the lower, and so the other differences of places. Sn.

And

22. Those figures that are like unto the same, are like betweene themselves.

This third consectary is manifest out of the definition of like figures. For the similitude of two figures doth conclude both the same equality in angles and proportion of sides betweene themselves.

And

23. If unto the parts of a figure given, like parts and alike situate, be placed upon a bound given, a like figure and likely situate unto the figure given, shall bee made accordingly.

This fourth consectary teacheth out of the said definition, the fabricke and manner of making of a figure alike and likely situate unto a figure given. Sn.

24. Like figures have a reason of their homologallor correspondent sides equally manifold unto their dimensions: and a meane proportionall lesse by one.

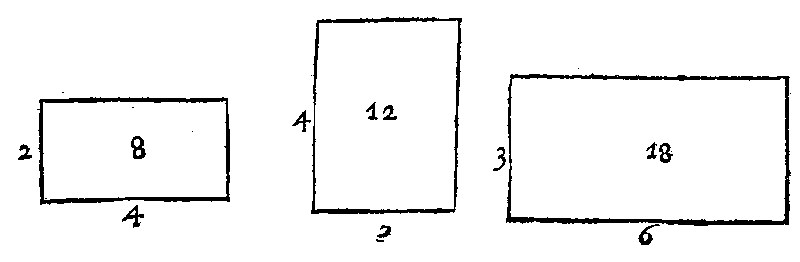
Plaine figures have but two dimensions, to witt Length, and Breadth: And therefore they have but a doubled reason of their homologall sides. Solids have three dimensions, videl. Length, Breadth, & thicknesse: therefore they shall have a treabled reason of their homologall or correspondent sides. In 8. and 18. the two plaines given, first the angles are equall: secondly, their homolegall side 2. and 4. and 3. and 6. are proportionall. Therefore the reason of 8. the first figure, unto 18. the second, is as the reason is of 2. unto 3. doubled. But the reason of 2. unto 3. doubled, by the 3. chap. ij. of Arithmeticke, is of 4. to 9. (for 2/3 2/3 is 4/9.) Therefore the reason of 8. unto 18, that is, of the first figure unto the second, is of 4. unto 9. In Triangles, which are the halfes of rightangled parallelogrammes, there is the same truth, and yet by it selfe not rationall and to be expressed by numbers.

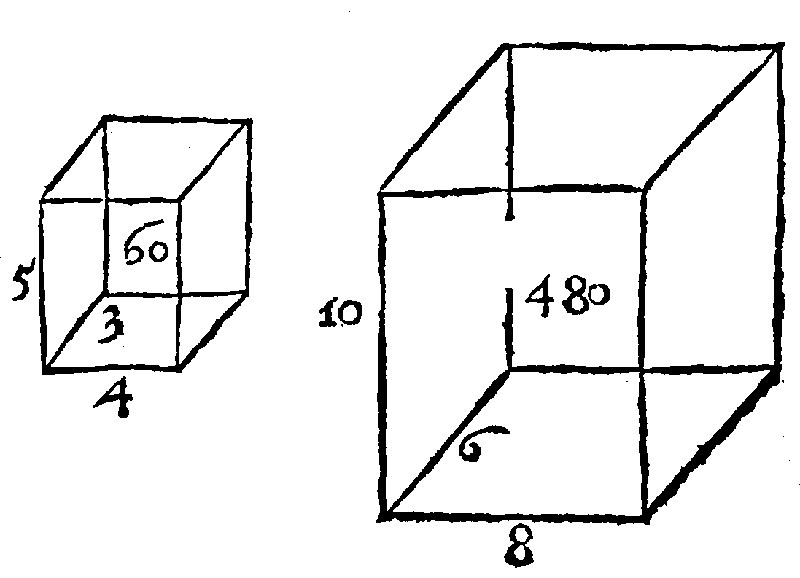
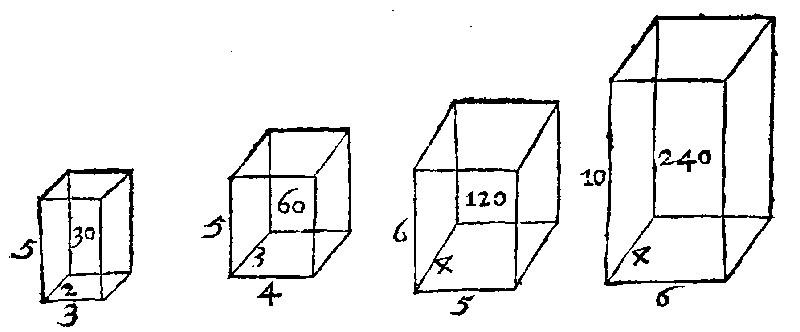
Said numbers are alike in the trebled reason of their homologall sides; As for example, 60. and 480. are like solids; and the solids also comprehended in those numbers are like-solids, as here thou seest: Because their sides, 4. 3. 5. and 8. 6. 10. are proportionall betweene themselves. But the reason of 60. to 480. is the reason of 4. to 8. trebled, thus 4/8 4/8 4/8 = 64/512; that is of 1. unto 8. or octupla, which you shall finde in the dividing of 480. by 60.

Thus farre of the first part of this element: The second, that like figurs have a meane, proportional lesse by one, then are their dimensions, shall be declared by few words. For plaines having but two dimensions, have but one meane proportionall, solids having three dimensions, have two meane proportionalls. The cause is onely Arithmeticall, as afore. For where the bounds are but 4. as they are in two plaines, there can be found no more but one meane proportionall, as in the former example of 8. and 18. where the homologall or correspondent sides are 2. 3. and 4. 6.

Therefore,

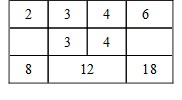
Againe by the same rule, where the bounds are 6. as they are in two solids, there may bee found no more but two meane proportionalls: as in the former solids 30. and 240. where the homologall or correspondent sides are 2. 4. 3. 6. 5. 10.

Therefore,

Therefore,

25. If right lines be continually proportionall, more by one then are the dimensions of like figures likelily situate unto the first and second, it shall be as the first right line is unto the last, so the first figure shall be unto the second: And contrariwise.

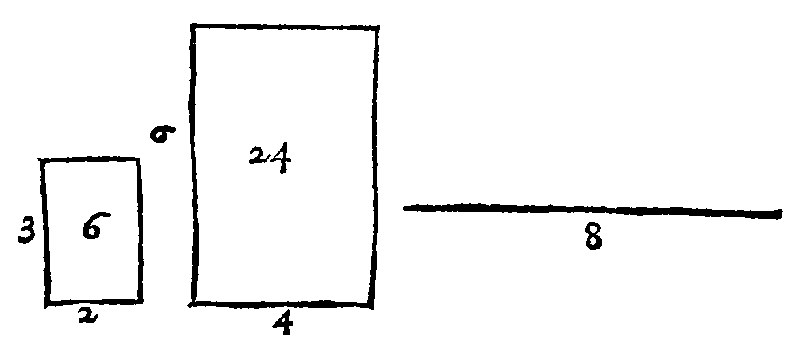
Out of the similitude of figures two consectaries doe arise, in part only, as is their axiome, rationall and expressable by numbers. If three right lines be continually proportionall, it shall be as the first is unto the third: So the rectilineall figure made upon the first, shall be unto the rectilineall figure made upon the second, alike and likelily situate. This may in some part be conceived and understood by numbers. As for example, Let the lines given, be 2. foot, 4. foote, and 8 foote. And upon the first and second, let there be made like figures, of 6. foote and 24. foote; So I meane, that 2. and 4. be the bases of them. Here as 2. the first line, is unto 8. the third line: So is 6. the first figure, unto 24. the second figure, as here thou seest.

Againe, let foure lines continually proportionall, be 1. 2. 4. 8. And let there bee two like solids made upon the first and second: upon the first, of the sides 1. 3. and 2. let it be 6. Upon the second, of the sides 2. 6. and 4. let it be 48. As the first right line 1. is unto the fourth 8. So is the figure 6. unto the second 48. as is manifest by division. The examples are thus.

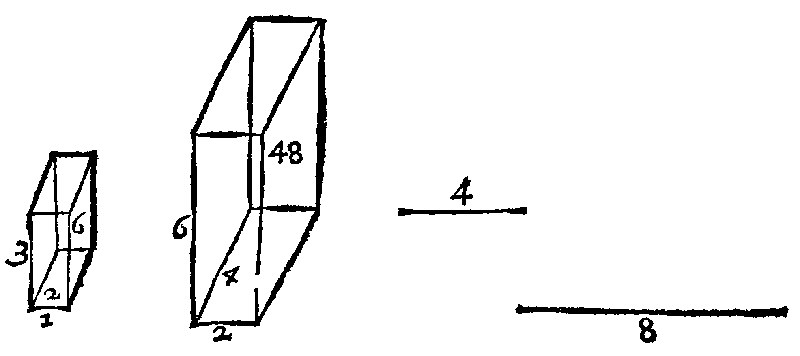
Moreover by this Consectary a way is laid open leading unto the reason of doubling, treabling, or after any manner way whatsoever assigned increasing of a figure given. For as the first right line shall be unto the last: so shall the first figure be unto the second.

And

26. If foure right lines bee proportionall betweene themselves: Like figures likelily situate upon them, shall be also proportionall betweene themselves: And contrariwise, out of the 22. p vj. and 37. p xj.

The proportion may also here in part bee expressed by numbers: And yet a continuall is not required, as it was in the former.

In Plaines let the first example be, as followeth.

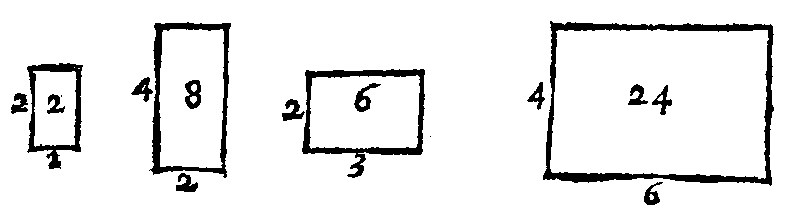
The cause of proportionall figures, for that twice two figures have the same reason doubled.

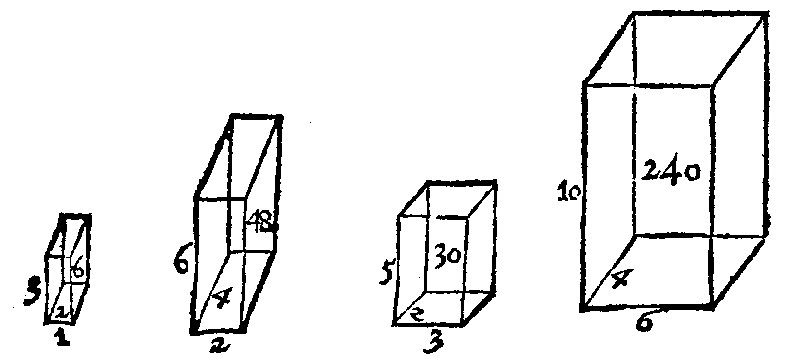
In Solids let this bee the second example. And yet here the figures are not proportionall unto the right lines, as before figures of equall heighth were unto their bases, but they themselves are proportionall one to another. And yet are they not proportionall in the same kinde of proportion.

The cause also is here the same, that was before: To witt, because twice two figures have the same reason trebled.

27. Figures filling a place, are those which being any way set about the same point, doe leave no voide roome.

This was the definition of the ancient Geometers, as appeareth out of Simplicius, in his commentaries upon the 8. chapter of Aristotle's iij. booke of Heaven: which kinde of figures Aristotle in the same place deemeth to bee onely ordinate, and yet not all of that kind. But only three among the Plaines, to witt a Triangle, a Quadrate, and a Sexangle: amongst Solids, two; the Pyramis, and the Cube. But if the filling of a place bee judged by right angles, 4. in a Plaine, and 8. in a Solid, the Oblong of plaines, and the Octahedrum of Solids shall (as shall appeare in their places) fill a place; And yet is not this Geometrie of Aristotle accurate enough. But right angles doe determine this sentence, and so doth Euclide out of the angles demonstrate, That there are onely five ordinate solids; And so doth Potamon the Geometer, as Simplicus testifieth, demonstrate the question of figures filling a place. Lastly, if figures, by laying of their corners together, doe make in a Plaine 4. right angles, or in a Solid 8. they doe fill a place.

Of this probleme the ancient geometers have written, as we heard even now: And of the latter writers, Regiomontanus is said to have written accurately; And of this argument Maucolycus hath promised a treatise, neither of which as yet it hath beene our good hap to see.

Neither of these are figures of this nature, as in their due places shall be proved and demonstrated.

28. A round figure is that, all whose raies are equall.

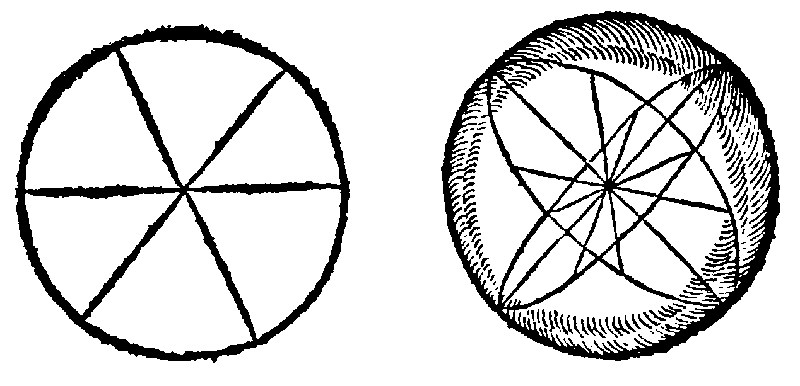
Such in plaines shall the Circle be, in Solids the Globe or Spheare. Now this figure, the Round, I meane, of all Isoperimeters is the greatest, as appeared before at the 15. e. For which cause Plato, in his Timæus or his Dialogue of the World said; That this figure is of all other the greatest. And therefore God, saith he, did make the world of a sphearicall forme, that within his compasse it might the better containe all things: And Aristotle, in his Mechanicall problems, saith; That this figure is the beginning, principle, and cause of all miracles. But those miracles shall in their time God willing, be manifested and showne.

Rotundum, a Roundle, let it be here used for Rotunda figura, a round figure. And in deede Thomas Finkius or Finche, as we would call him, a learned Dane, sequestring this argument from the rest of the body of Geometry, hath intituled that his worke De Geometria rotundi, Of the Geometry of the Round or roundle.

29. The diameters of a roundle are cut in two by equall raies.

The reason is, because the halfes of the diameters, are the raies. Or because the diameter is nothing else but a doubled ray: Therefore if thou shalt cut off from the diameter so much, as is the radius or ray, it followeth that so much shall still remaine, as thou hast cutte of, to witt one ray, which is the other halfe of the diameter. Sn.

And here observe, That Bisecare, doth here, and in other places following, signifie to cutte a thing into two equall parts or portions; And so Bisegmentum, to be one such portion; And Bisectio, such a like cutting or division.

30. Rounds of equall diameters are equall. Out of the 1. d. iij.

Circles and Spheares are equall, which have equall diameters. For the raies, which doe measure the space betweene the Center and Perimeter, are equall, of which, being doubled, the Diameter doth consist. Sn.

The fifth Booke, of Ramus his Geometry, which is of Lines and Angles in a plaine Surface

1. A lineate is either a Surface or a Body.

Lineatum, (or Lineamentum) a magnitude made of lines, as was defined at 1. e. iij. is here divided into two kindes: which is easily conceived out of the said definition there, in which a line is excluded, and a Surface & a body are comprehended. And from hence arose the division of the arte Metriall into Geometry, of a surface, and Stereometry, of a body, after which maner Plato in his vij. booke of his Common-wealth, and Aristotle in the 7. chapter of the first booke of his Posteriorums, doe distinguish betweene Geometry and Stereometry: And yet the name of Geometry is used to signifie the whole arte of measuring in generall.

2. A Surface is a lineate only broade. 5. d j.

As here aeio. and uysr. The definition of a Surface doth comprehend the distance or dimension of a line, to witt Length: But it addeth another distance, that is Breadth. Therefore a Surface is defined by some, as Proclus saith, to be a magnitude of two dimensions. But two doe not so specially and so properly define it. Therefore a Surface is better defined, to bee a magnitude onely long and broad. Such, saith Apollonius, are the shadowes upon the earth, which doe farre and wide cover the ground and champion fields, and doe not enter into the earth, nor have any manner of thicknesse at all.

Epiphania, the Greeke word, which importeth onely the outter appearance of a thing, is here more significant, because of a Magnitude there is nothing visible or to bee seene, but the surface.

3. The bound of a surface is a line. 6. d j.

The matter in Plaines is manifest. For a three cornered surface is bounded with 3. lines: A foure cornered surface, with foure lines, and so forth: A Circle is bounded with one line. But in a Sphearicall surface the matter is not so plaine: For it being whole, seemeth not to be bounded with a line. Yet if the manner of making of a Sphearicall surface, by the conversiō or turning about of a semiperiphery, the beginning of it, as also the end, shalbe a line, to wit a semiperiphery: And as a point doth not only actu, or indeede bound and end a line: But is potentia, or in power, the middest of it: So also a line boundeth a Surface actu, and an innumerable company of lines may be taken or supposed to be throughout the whole surface. A Surface therefore is made by the motion of a line, as a Line was made by the motion of a point.

4. A Surface is either Plaine or Bowed.

The difference of a Surface, doth answer to the difference of a Line, in straightnesse and obliquity or crookednesse.

Obliquum, oblique, there signified crooked; Not right or straight: Here, uneven or bowed, either upward or downeward. Sn.

5. A plaine surface is a surface, which lyeth equally betweene his bounds, out of the 7. d j.

As here thou seest in aeio. That therefore a Right line doth looke two contrary waies, a Plaine surface doth looke all about every way, that a plaine surface should, of all surfaces within the same bounds, be the shortest: And that the middest thereof should hinder the sight of the extreames. Lastly, it is equall to the dimension betweene the lines: It may also by one right line every way applyed be tryed, as Proclus at this place doth intimate.

Planum, a Plaine, is taken and used for a plaine surface: as before Rotundum, a Round, was used for a round figure.

Therefore,

6. From a point unto a point we may, in a plaine surface, draw a right line, 1 and 2. post. j.

Three things are from the former ground begg'd: The first is of a Right line. A right line and a periphery were in the ij. booke defined: But the fabricke or making of them both, is here said to bee properly in a plaine.

The fabricke or construction of a right line is the 1. petition. And justly is it required that it may bee done onely upon a plaine: For in any other surface it were in vaine to aske it. For neither may wee possibly in a sphericall betweene two points draw a right line: Neither may wee possibly in a Conicall and Cylindraceall betweene any two points assigned draw a right line. For from the toppe unto the base that in these is only possible: And then is it the bounde of the plaine which cutteth the Cone and Cylinder. Therefore, as I said, of a right plaine it may onely justly bee demanded: That from any point assigned, unto any point assigned, a right line may be drawne, as here from a unto e.

Now the Geometricall instrument for the drawing of a right plaine is called Amussis, & by Petolemey, in the 2. chapter of his first booke of his Musicke, Regula, a Rular, such as heere thou seest.

And from a point unto a point is this justly demanded to be done, not unto points; For neither doe all points fall in a right line: But many doe fall out to be in a crooked line. And in a Spheare, a Cone & Cylinder, a Ruler may be applyed, but it must be a sphearicall, Conicall, or Cylindraceall. But by the example of a right line doth Vitellio, 2 p j. demaund that betweene two lines a surface may be extended: And so may it seeme in the Elements, of many figures both plaine and solids, by Euclide to be demanded; That a figure may be described, at the 7. and 8. e ij. Item that a figure may be made vp, at the 8. 14. 16. 23. 28. p. vj. which are of Plaines. Item at the 25. 31. 33. 34. 36. 49. p. xj. which are of Solids. Yet notwithstanding a plaine surface, and a plaine body doe measure their rectitude by a right line, so that jus postulandi, this right of begging to have a thing granted may seeme primarily to bee in a right plaine line.

Now the Continuation of a right line is nothing else, but the drawing out farther of a line now drawne, and that from a point unto a point, as we may continue the right line ae. unto i. wherefore the first and second Petitions of Euclide do agree in one.

And

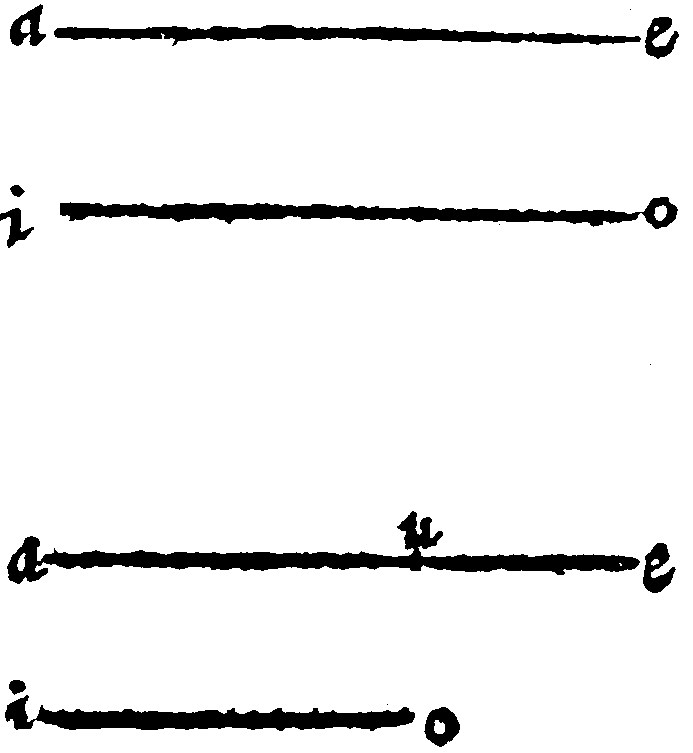
7. To set at a point assigned a Right line equall to another right line given: And from a greater, to cut off a part equall to a lesser. 2. and 3. p j.

As let the Right line given be ae. And to i. a point assigned, grant that io. equall to the same ae. may bee set. Item, in the second example, let ae. bee greater then io. And let there be cut off from the same ae. by applying of a rular made equall to io. the lesser, portion au. as here. For if any man shall thinke that this ought only to be don in the minde, hee also, as it were, beares a ruler in his minde, that he may doe it by the helpe of the ruler. Neither is the fabricke in deede, or making of one right equal to another: And the cutting off from greater Right line, a portion equall to a lesser, any whit harder, then it was, having a point and a distance given, to describe a circle: Then having a Triangle, Parallelogramme, and semicircle given, to describe or make a Cone, Cylinder, and spheare, all which notwithstanding Euclide did account as principles.

Therefore,

8. One right line, or two cutting one another, are in the same plaine, out of the 1. and 2. p xj.

One Right line may bee the common section of two plaines: yet all or the whole in the same plaine is one: And all the whole is in the same other: And so the whole is the same plaine. Two Right lines cutting one another, may bee in two plaines cutting one of another; But then a plaine may be drawne by them: Therefore both of them shall be in the same plaine. And this plaine is geometrically to be conceived: Because the same plaine is not alwaies made the ground whereupon one oblique line, or two cutting one another are drawne, when a periphery is in a sphearicall: Neither may all peripheries cutting one another be possibly in one plaine.