The Way To Geometry

The other five triangles beneath shall after the like manner be concluded to be equilaters. Therefore one shall be for all, to wit, ibe, by drawing the raies di, and de. For ib, whose power, as afore, is as much as the sides of the sexangle, and decangle, shall be the side of the quinquangle: And in like sort be, being of equall power with de, and do, the sides of the sexangle and decangle, shall be the side of the quinquangle. Wherefore the triangle ebi, is an equilater: And the foure other in like manner may be shewed to be equilaters. Therefore all the side of the twenty triangles, seeing they are equall, they shall be equilater triangles: And by the 8 e, vij. equall.

17 The diagony of an icosaedrū is irrational unto the side.

This is the fourth example of irrationality, or incommensurability. The first was of the Diagony and side of a square or quadrate. The second was of the segments of a line proportionally cut. The third of the Diameter of a circle and the side of a quinquangle.

And

18 The power of the diagony of an icosaedrum is five times as much as the ray of the circle.

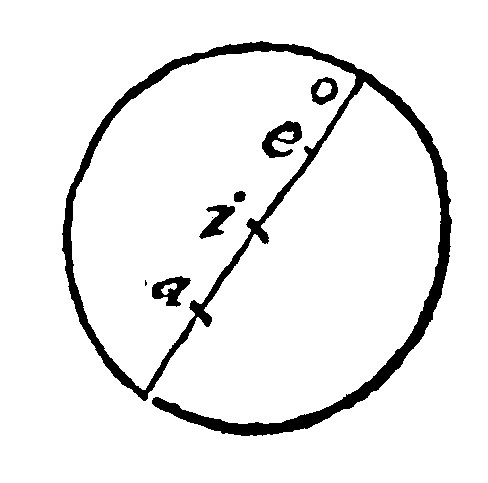
For by the 13 e, xviij. the line continually made of the side of the sexangle and decangle is cut proportionally, and the greater segment is the side of the sexangle: As here. Let the perpendicular ae, be cut into two equall parts in i. Then eo, that is the lesser segment continued with the halfe of the greater, that is, with ie. it shall by the 6 e xiiij, be of power five times so great as is the power of the same halfe. Therefore seeing that io, the halfe of the diagony is of power fivefold to the halfe: the whole diagony shall be of power fivefold to the whole cut.

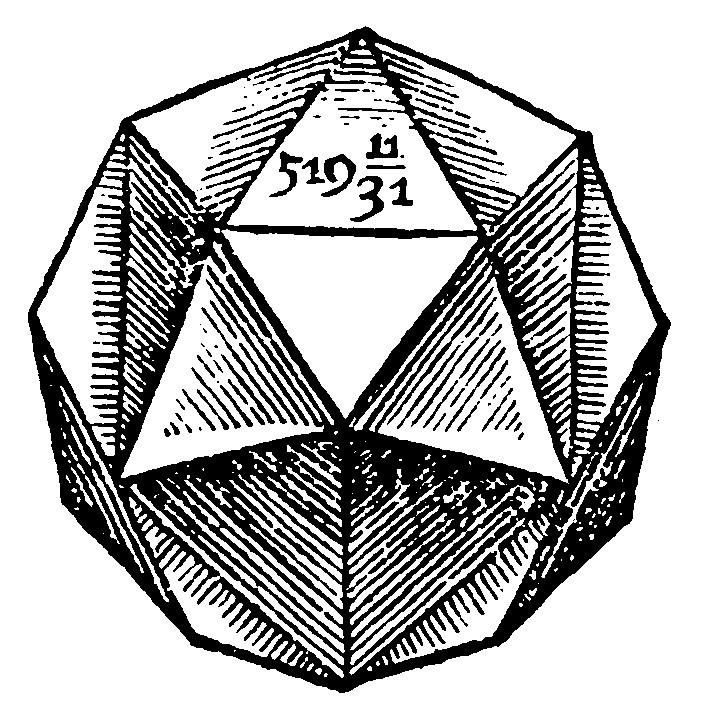
And from hence also shall be the geodesy of the Icosaedrum. For the finding out of the heighth of the pyramis, there is the semidiagony of the side of the decangle and the halfe ray of the circle: But the side of the decangle is a right line subtending the halfe periphery of the side of the quinquangle, or else the greater segment of the ray proportionally cut. For so it may be taken Geometrically, and reckoned for his measure. Therefore if the quadrate of the side of the decangle, be taken out of the quadrate of the side of the quinquangle, there shall by the 15 e xviij, remaine the quadrate of the sexangle, that is of the ray. The side of the decangle (because the side of the quinquangle here is 6) shall be 3.3/35 to wit a right line subtending the halfe periphery. Now the halfe ray shall thus be had. The quadrates of the quinquangle and decangle are 36, and 9.639/1225. And this being subducted fro that, the remaine 26.386/1225 by the 15 e xviij, shall be the quadrate or square of the sexangle: And the side of it, 5, and almost 5/7 shall be the ray: The halfe ray therefore shall be 2.6/7. To the side of the decangle 3.3/35 adde 2.6/7: the whole shal be 5.33/35 for the semi-diagony of the Icosaedrum. The ray of the circle circumscribed about the triangle, is by the 12 e xviij, the same which was before 3.3/7 to wit of the quadrate 12. Therefore if the quadrate of the circular ray, be taken out of the quadrate of the halfe diagony, there shall remaine the quadrate of the heighth and perpendicular: the quadrate of the halfe-diagony is 35.389/1225: the quadrate of the circular ray is 12. This taken out of that beneath 23.639/1225: whose side is almost 5, for the perpendicular and heighth proposed: From whence now the Pyramis is esteemed. The case of a triangular pyramis is 15.18/31. The Plaine of this base and the third part of the heighth is 25.30/31 for the solidity of one Pyramis. This multiplyed by 20 maketh 519.11/31 for the summe or whole solidity of the Icosaedum. And this is the geodesy or manner of measuring of an Icosaedrum.

19. A mingled ordinate polyedrum of a quinquangular base is that which is comprehended of 12 quinquangles, and it is called a Dodecaedrum.

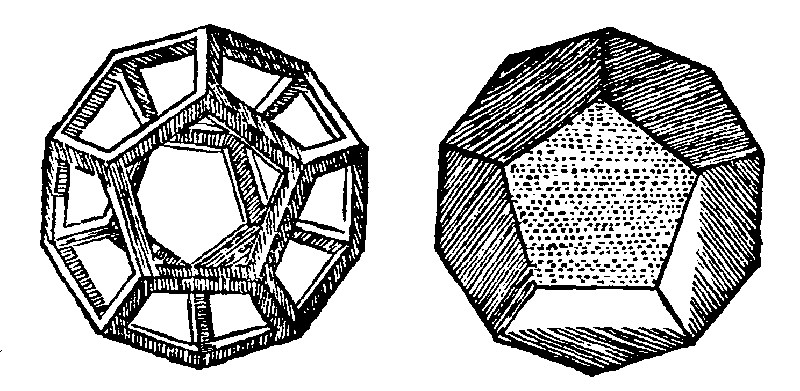
Therefore

20. The sides of a Dodecaedrum are 30, the plaine angles 60. the solid 20.

And

21. If 12 ordinate equall quinquangles be joyned with solid angles, they shall comprehend a Dodecaedrum.

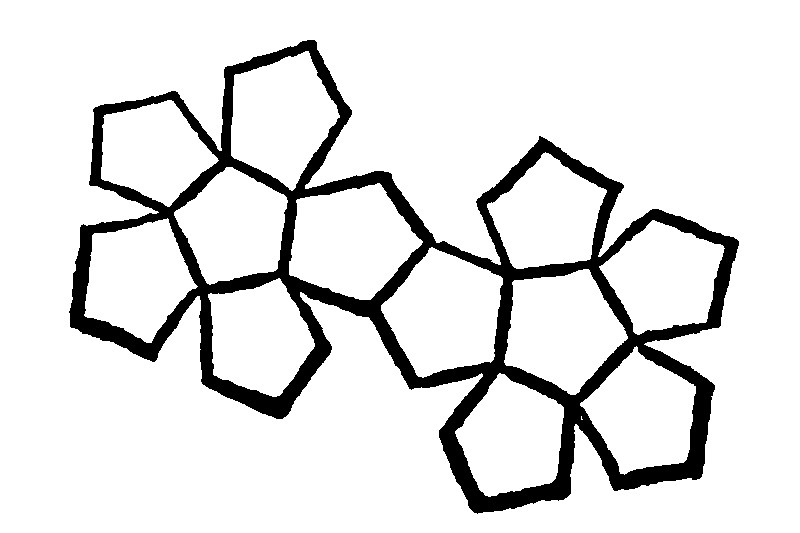
As here thou seest.

22. If the sides of a cube be with right lines cut into two equall parts, and three bisegments of the bisecants in the abbuting plaines, neither meeting one the other, nor parallell one unto another, two of one, the third of that next unto the remainder, be so proportionally cut that the lesser segments doe bound the bisecant: three lines without the cube perpendicular unto the sayd plaines from the points of the proportionall sections, equall to the greater segment knit together, two of the same bisecant, betweene themselves and with the next angles of cube; the third with the same angles, they shall comprehend a dodecaedrum. 17 p xiij.

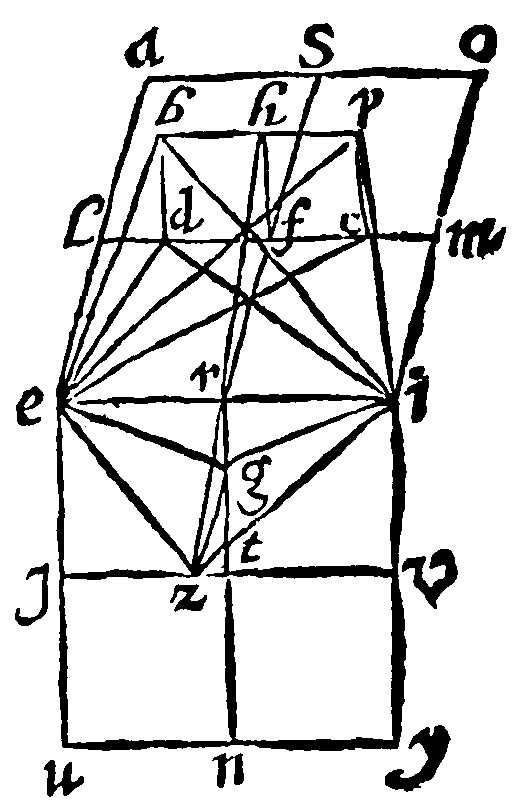
Let there be two plaines for a cube for all, that one quinquangle for twelve may be described, and they abutting one upon another, aeio, and euyi, having their sides halfed by the bisecantes, sr, lm, rn, jv: And the three bisegments or portions of the bisegments lm, and rn, neither concurring or meeting, nor parallell one to another; two of the said lm, to wit, fl, and fm: The third next unto the remainder, that is lr. And let each bisegment be cut proportionally in the points d, c, g; so that the lesser segments doe bound the bisecant, to wit, dl, cm, and gr. Lastly let there be three perpendiculars from the points db, cg, to the said d, cp, gz: And the two first knit one to another, by bp: And againe with the angles of the cube, by be, and pi: The third knit with the same angles, by ze, and zi: And let all the plaines be made up. I say first, that the five sides bp, pi, iz, ze, and eb are equall; Because, every one of them severally are the doubles of the same greater segment. For in drawing the right lines de and eg, ig, it shall be plaine of two of them; And after the same manner of the rest. First therefore cd, and bp, are equall by the 6 e xxj, and by the 27 e v. Therefore bp, is the double of the greater segment. Then the whole fl, cut proportionally, and the lesser segment dl, they are by the 7 e xiiij, of treble power to the greater fd, that is, by the fabricke db. Therefore le wich is equall to lf, the line cut, and ld, are of treble power to the same db: But by the 9 e xij, de is of as much power as le, and ld too. Therefore de is of treble power to db. Therefore both ed, and db, are of quadruple power to db. But be, by the 9 e xij, is of as much power as ed, and db. And therefore be, is of quadruple value to db: And by the 14 e xij, it is the double of the said db. Therefore the two sides eb, and bp, are equall: And by the same argument pi, iz, and ze, are equall. Therefore the quinquangle is equilater.

I say also that it is a Plaine quinquangle: For it may be said to be an oblique quinquangle; and to be seated in two plaines. Let therefore fh be parallell to db, and cp: and be equall unto them. And let hz, be drawne: This hz shall be cut one line, by the 14 e vij. For as the whole tr, that is rf, is unto the greater segment that is to fh: so fh, that is zg, is unto gr. And two paire of shankes fh, gr, fc, gz, by the 6 e xxj, are alternely or crosse-wise parallell. Therefore their bases are continuall.

Hitherto it hath beene prooved that the quinquangle made is an equilater and plaine: It remaineth that it bee prooved to be Equiangled. Let therefore the right lines ep, and ec, be drawne: I say that the angles, pbe, and ezi, are equall: Because they have by the construction, the bases of equall shankes equall, being to wit in value the quadruple of le. For the right line lf, cut proportionally, and increased with the greater segment df, that is fc, is cut also proportionally, by the 4 e xiiij, and by the 7 e xiiij, the whole line proportionally cut, and the lesser segment, that is cp, are of treble value to the greater fl, that is of the sayd le. Therefore el, and lc, that is ec, and cp, that is ep, is of quadruple power to el: And therefore by the 14 e xij, it is the double of it: And ei, it selfe in like manner, by the fabricke or construction, is the double of the same. Therefore the bases are equall. And after the same manner, by drawing the right lines id, and ib, the third angle bpi, shall be concluded to be equal to the angle ezi. Therefore by the 13 e xiiij, five angles are equall.

23. The Diagony is irrationall unto the side of the dodecahedrum.

This is the fifth example of irrationality and incommensurability. The first was of the diagony and side of a quadrate or square. The second was of a line proportionally cut and his segments: The third is of the diameter of a Circle and the side of an inscribed quinquangle. The fourth was of the diagony and side of an icosahedrum. The fifth now is of the diagony and side of a dodecahedrum.

24 If the side of a cube be cut proportionally, the greater segment shall be the side of a dodecahedrum.

For that hath beene told you even now.

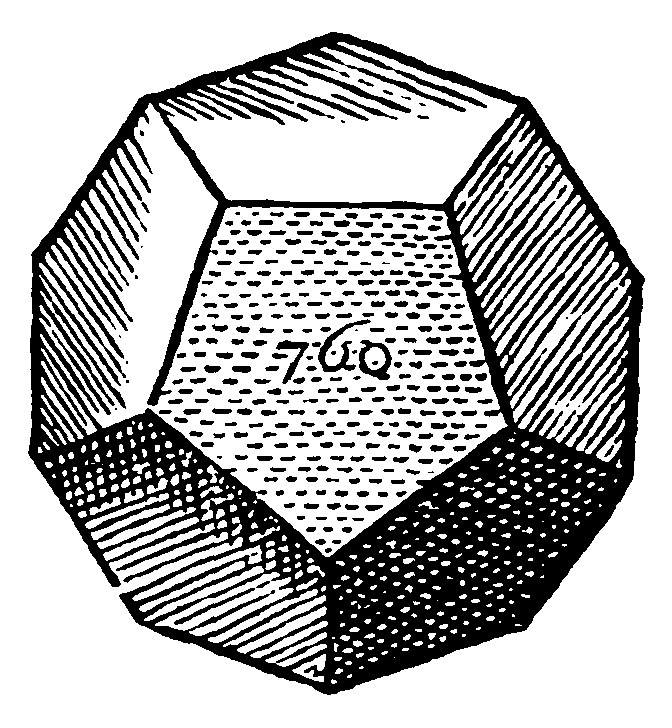
But from hence also doth arise the geodesy or māner of measuring of a dodecahedrum. For if the quadrate of the line subtending the angle of a quinquangle be trebled, the half of the treble shall be the side of the semidiagony of the dodecahedrum: Because by the 6 e xxiiij, the diagony of the cube, that is of the dodecahedrum is of treble power to the side of the cube. But if the quadrate of the side of the decangle be taken out of the quadrate of the side of the quinquangle; The side of the remainder shall be the ray of the circle circumscribed about a quinquangle. Lastly if the quadrate of the ray, be taken of the quadrate of the half-diagony; the side of the remainder shall be the heighth of perpendicular. As if the side of the decangle be 7.3/5: The quadrate of that shall be 57.19/25: the treble of which is 173.7/25 whose side is about 13.107/131 for the side of the Dodecahedrum, therefore 6.119/131 the halfe shall be the semidiagony of the dodecahedrum. The ray of the Circle shall now thus be found. If the quadrate of the side of the decangle be taken out of the quadrate of the side of the sexangle; the side of the remainder, shall be the Ray of the Circle, by the 15 and 9 e xviij. As here the side of the Quinquangle is 4.2/3. The side of the Decangle 2.2/5: And the quadrates therefore are 21.7/9, and 5.19/25. This subducted from that leaveth 16.4/225 whose side is 4.2/15 for the Ray of the Circle.

The semidiagony and ray of the circle thus found, the altitude remaineth. Take out therefore the quadrate of the ray of the circle, 16.4/225 out of the quadrate of the semidiagony 47.12458/17161, the side of the remainder 31.2714406/3861225 is for the altitude or heighth: whose 1/3 is 5/3. The quinquangled base is almost 38. Which multiplied by 5/3 doth make 63.1/3 for the solidity of one Pyramis; which multiplied by 12, doth make 760. for the soliditie of the whole dodecaedrum.

25 There are but five ordinate solid plaines.

This appeareth plainely out of the nature of a solid angle, by the kindes of plaine figures. Of two plaine angles a solid angle cannot be comprehended. Of three angles of an ordinate triangle is the angle of a Tetrahedrum comprehended: Of foure, an Octahedrum: Of five, an Icosahedrum: Of sixe none can be comprehended: For sixe such like plaine angles, are equall to 12 thirds of one right angle, that is to foure right angles. But plaine angles making a solid angle, are lesser than foure right angles, by the 8 e xxij. Of seven therefore, and of more it is, much lesse possible. Of three quadrate angles the angle of a cube is comprehended: Of 4. such angles none may be comprehended for the same cause. Of three angles of an ordinate quinquangle, is made the angle of a Dodecahedrum. Of 4. none may possibly be made; For every such angle: For every one of them severally doe countervaile one right angle and 1/5 of the same, Therefore they would be foure, and three fifths. Of more therefore much lesse may it be possible.

This demonstration doth indeed very accurately and manifestly appeare, Although there may be an innumerable sort of ordinate plaines, yet of the kindes of angles five onely ordinate bodies may be made; From whence the Tetrahedrum, Octahedrum, and Icosahedrum are made upon a triangular base: the Cube upon a quadrangular: And the Dodecahedrum, upon a quinquangular.

Of Geometry the twenty sixth Booke; Of a Spheare

1 An imbossed solid is that which is comprehended of an imbossed surface.

2. And it is either a spheare or a Mingled forme.

3. A speare is a round imbossement.

It may also be defined to be that which is comprehended of a sphearical surface. A sphearicall body in Greeke is called Sphæra, in Latine Globus, a Globe.

Therefore

4. A Spheare is made by the conversion of a semicircle, the diameter standing still. 14 d xj.

As here thou seest.

5. The greatest circle of a spheare, is that which cutteth the spheare into two equall parts.

Therefore

6. That circle which is neerest to the greatest, is greater than that which is farther off.

And

7. Those which are equally distant from the greatest are equall.

As in the example above written.

8. The plaine of the diameter and sixth part of the sphearicall is the solidity of the spheare.

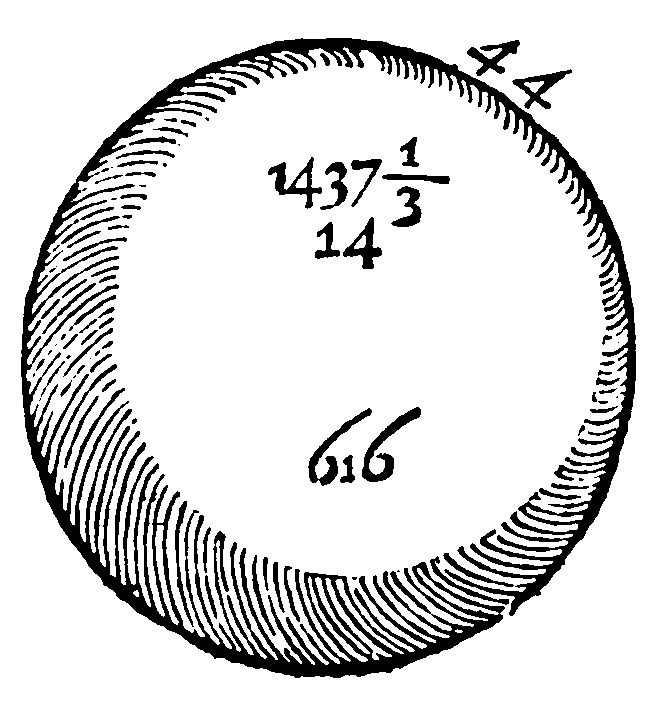
As before there was an analogy betweene a Circle and a Sphericall: so now is there betweene a Cube and a spheare. A cubicall surface is comprehended of sixe quadrate or square and equall bases: And a spheare in like manner is comprehended of sixe equall sphearicall bases compassing the cubicall bases. A cube is made by the multiplication of the sixth part of the base, by the side: And a spheare likewise is made by multiplying the sixth part of the sphearicall by the diameter, as it were by the side: so the plaine of 616/6 and 14, the diameter is 1437.1/3 for the solidity of the spheare.

Therefore

9. As 21 is unto 11, so is the cube of the diameter unto the spheare.

As here the Cube of 14 is 2744. For it was an easy matter for him that will compare the cube 2744, with the spheare, to finde that 2744 to be to 1437.1/3 in the least boundes of the same reason, as 21 is unto 11.

Thus much therefore of the Geodesy of the spheare: The geodesy of the Sectour and section of the spheare shall follow in the next place.

And

10. The plaine of the ray, and of the sixth part of the sphearicall is the hemispheare.

But it is more accurate and preciser cause to take the halfe of the spheare.

11. Spheares have a trebled reason of their diameters.

So before it was told you; That circles were one to another, as the squares of their diameters were one to another, because they were like plaines: And the diameters in circles were, as now they are in spheares, the homologall sides. Therefore seeing that spheres are figures alike, and of treble dimension, they have a trebled reason of their diameters.

12. The five ordinate bodies are inscribed into the same spheare, by the conversion of a semicicle having for the diameter, in a tetrahedrum, a right line of value sesquialter unto the side of the said tetrahedrum; in the other foure ordinate bodies, the diagony of the same orginate.

The Adscription of ordinate plaine bodies is unto a spheare, as before the Adscription plaine surfaces was into a circle; of a triangle, I meane, and ordinate triangulate, as Quadrangle, Quinquangle, Sexangle, Decangle, and Quindecangle. But indeed the Geometer hath both inscribed and circumscribed those plaine figures within a circle. But these five ordinate bodies, and over and above the Polyhedrum the Stereometer hath onely inscribed within the spheare. The Polyhedrum we have passed over, and we purpose onely to touch the other ordinate bodies.

13 Out of the reason of the axeltree of the sphearicall the sides of the tetraedrum, cube, octahedrum and dodecahedrum are found out.

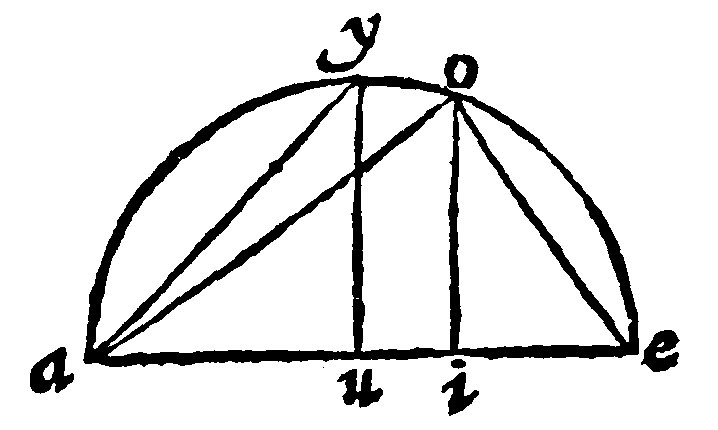
The axeltree in the three first bodies is rationall unto the side, as was manifested in the former. For it is of the sesquialter valew unto the side of the tetrahedrum; of treble, to the side of the cube: Of double, to the side of the Octahedrum. Therefore if the axis ae, be cut by a double reason in i: And the perpendicular io, be knit to a, and e, shall be the side of the tetrahedrum; and oe, of the cube, as was manifest by the 10 e viij, and 25 iiij: And the greater segment of the side of the cube proportionally cut, is by the 24 e, xxv.

If the same axis be cut into two halfes, as in u: And the perpendicular uy, be erected: And y, and a, be knit together, the same ya, thus knitting them, shall be the side of the Octahedrum, as is manifest in like manner, by the said 10 e, viij, and 25 e iiij.

The side of the Icosahedrum is had by this meanes.

14. If a right line equall to the axis of the sphearicall, and to it from the end of the perpendicular be knit unto the center, a right line drawne from the cutting of the periphery unto the said end shall be the side of the Icosahedrum.

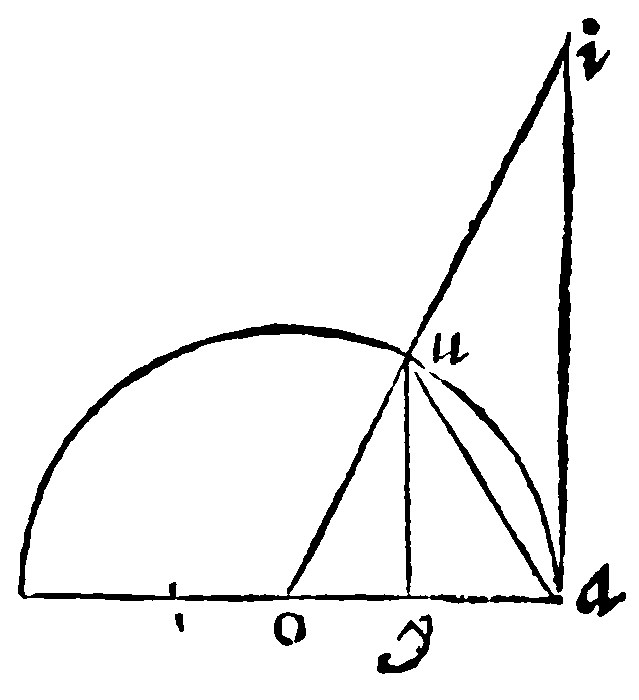
As here let the Axis ae; be the diameter of the circle aue, and ai, equall to the same axis, and perpendicular from the end, be knit unto the center, by the right line io: A right drawne from the section u, unto a, shall be the side of the Icosahedrum. From u, let the perpendicular uy, be drawne: Here the two triangles iao, & uyo, are equiangles by the 13 e, vij. Therfore by the 12 e, vij. as ia, is unto ao: so is uy, unto yo. But ia, is the double of the said ao: Therefore uy, is the double of the same yo: Therefore by the 14 e, xij, it is of quadruple power unto it: And therefore also uy, and yo, that is, by the 9 e xij, uo, that is againe by the 28 e, iiij, ao, is of quintuple power to yo. But yo, is lesser than ao, that is, than oe: Let therefore os, be cut off equall to it. Now as the halfe of ao, is of quintuple valew to the halfe of yo: so the double ae, is of quintuple power to the double ys. Therefore, by the 18 e xxv. seeing that the diagony ae, is of quintuple power to ys; the said ys, shall be the side of the sexangle inscribed into a circle, circumscribing the quinquangle of the Icosahedrum. But the perpendicular uy, is equall to ys; because each of them is the double of yo. Wherefore uy, is the side of the sexangle. But ay, is the side of the Decangle: For it is equall to se: Because if from equall rayes ao, and oe, you take equall portions oy, and os: There shall remaine equall, ya, and se. And the Diagony of an Icosahedrum by the 16 e xxv, is compounded of the side of the sexangle, continued at each end with the side of the decangle. Wherefore ay, is the side of the decangle. Lastly, ua, whose power is as much as the sides of the sexangle and decangle, by the 15. e, xviij, shall be the side of an Icosahedrum.

15 Of the five ordinate bodies inscribed into the same spheare, the tetrahedrum in respect of the greatnesse of his side is first, the Octahedrum, the second; the Cube, the third; the Icosahedrum, the fourth; and the Dodecahedrum, the fifth.

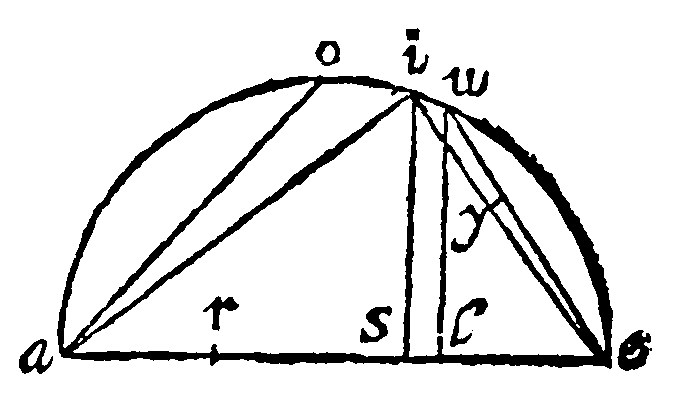
As it will plainely appeare, if all of them be gathered into one, thus. For ai, the side of the Tetrahedrum, subtendeth a greater periphery than ao, the side of the Octahedrum; And ao, a greater than ie, the side of the Cube; because it subtendeth but the halfe: And ie, greater than ue, the side of the Icosahedrum: And ue, greater than ye, the side of Dodecahedrum.

The latter, Euclide doth demonstrate with a greater circumstance. Therefore out of the former figures and demonstrations, let here be repeated, The sections of the axis first into a double reason in s: And the side of the sexangle rl: And the side of the Decangle ar, inscribed into the same circle, circumscribing the quinquangle of an icosahedrum: And the perpendiculars is, and ul.

Here the two triangles aie, and ies, are by the 8 e, viij. alike; And as se, is unto ei: So is ie, unto ea: And by 25 e, iiij, as se, is to ea: so is the quadrate of se, to the quadrate of ei: And inversly or backward, as ae, is to se: so is the quadrate of ie, to the quadrate of se. But ae, is the triple of se. Therefore the quadrate of ie, is the triple of se. But the quadrate of as, by the grant, and 14 e xij, the quadruple of the quadrate of se. Therefore also it is greater than the quadrate of ie: And the right line as, is greater than ie, and al, therefore is much greater. But al, is by the grant compounded of the sides of the sexangle and decangle rl, and ar. Therefore by the 1 c. 5 e, 18. it is cut proportionally: And the greater segment is the side of the sexangle, to wit, rl: And the greater segment of ie, proportionally also cut, is ye. Therefore the said rl, is greeter than ye: And even now it was shewed ul, was equall to rl. Therefore ul, is greater than ye: But ue, the side of the Icosahedrum, by 22. e vj. is greater than ul. Therefore the side of the Icosahedrum is much greater, then the side of the dodecahedrum.

Of Geometry the twenty seventh Book; Of the Cone and Cylinder

1 A mingled solid is that which is comprehended of a variable surface and of a base.

For here the base is to be added to the variable surface.

2 If variable solids have their axes proportionall to their bases, they are alike. 24. d xj.