The Creativity Code: How AI is learning to write, paint and think

This is the basic core of the algorithm. There are a few extra subtleties that need to be introduced to get the algorithm working in its full glory. For example, the algorithm needs to take into account anomalies like websites that don’t link to any other websites and become sinks for the balls being redistributed. But at its heart is this simple idea.

Although the basic engine is very public, there are parameters inside the algorithm that are kept secret and change over time, and which make the algorithm a little harder to hack. But the fascinating thing is the robustness of the Google algorithm and its imperviousness to being gamed. It is very difficult for a website to do anything on its own site that will increase its rank. It must rely on others to boost its position. If you look at the websites that Google’s page rank algorithm scores highly, you will see a lot of major news sources and university websites like Oxford and Harvard. This is because many outside websites will link to findings and opinions on university websites, because the research we do is valued by many people across the world.

Interestingly this means that when anyone with a website within the Oxford network links to an external site, the link will cause a boost to the external website’s page rank, as Oxford is sharing a bit of its huge prestige (or cache of balls) with that website. This is why I often get requests to link from my website in the maths department at Oxford to external websites. The link will help increase the external website’s rank and, it is hoped, make it appear on the first page of a Google search, the ultimate holy grail for any website.

But the algorithm isn’t immune to clever attacks by those who understand how the mathematics works. For a short period in the summer of 2018, if you googled ‘idiot’ the first image that appeared was that of Donald Trump. Activists had understood how to exploit the powerful position that the website Reddit has on the internet. By getting people to vote for a post on the site containing the words ‘idiot’ and an image of Trump, the connection between the two shot to the top of the Google ranking. The spike was smoothed out over time by the algorithm rather than by manual intervention. Google does not like to play God but trusts in the long run in the power of its mathematics.

The internet is of course a dynamic beast, with new websites emerging every nanosecond and new links being made as existing sites are shut down or updated. This means that page ranks need to change dynamically. In order for Google to keep pace with the constant evolution of the internet, it must regularly trawl through the network and update its count of the links between sites using what it rather endearingly calls ‘Google spiders’.

Tech junkies and sports coaches have discovered that this way of evaluating the nodes in a network can also be applied to other networks. One of the most intriguing external applications has been in the realm of football (of the European kind, which Americans think of as soccer). When sizing up the opposition, it can be important to identify a key player who will control the way the team plays or be the hub through which all play seems to pass. If you can identify this player and neutralise them early on in the game, then you can effectively close down the team’s strategy.

Two London-based mathematicians, Javier López Peña and Hugo Touchette, both football fanatics, decided to see whether Google’s algorithm might help analyse the teams gearing up for the World Cup. If you think of each player as a website and a pass from one player to another as a link from one website to another, then the passes made over the course of a game can be thought of as a network. A pass to a teammate is a mark of the trust you put in that player – players generally avoid passing to a weak teammate who might easily lose the ball, and you will only be passed to if you make yourself available. A static player will rarely be available for a pass.

They decided to use passing data made available by FIFA during the 2010 World Cup to see which players ranked most highly. The results were fascinating. If you analysed England’s style of play, two players, Steven Gerrard and Frank Lampard, emerged with a markedly higher rank than others. This reflects the fact that the ball very often went through these two midfielders: take them out and England’s game collapses. England did not get very far that year in the World Cup – they were knocked out early by their old nemesis, Germany.

Contrast this with the eventual winners: Spain. The algorithm shared the rank uniformly around the whole team, indicating that there was no clear hub through which the game was being played. This is a reflection of the very successful ‘total football’ or ‘tiki-taka’ style played by Spain, in which players constantly pass the ball around, a strategy that contributed to Spain’s ultimate success.

Unlike many sports in America that thrive on data, it has taken some time for football to take advantage of the mathematics and statistics bubbling underneath the game. But by the 2018 World Cup in Russia many teams boasted a scientist on board to crunch the numbers to understand the strengths and weaknesses of the opposition, including how the network of each team behaves.

A network analysis has even been applied to literature. Andrew Beveridge and Jie Shan took the epic saga A Song of Ice and Fire by George R. R. Martin, otherwise known as Game of Thrones. Anyone who knows the story will be aware that predicting which characters will make it through to the next volume, let alone the next chapter, is notoriously tricky, as Martin is ruthless at killing off even the best characters he has created.

Beveridge and Shan decided to create a network between characters in the books. They identified 107 key people who became the nodes of the network. The characters were then connected with weighted edges according to the strength of the relationship. But how can an algorithm assess the importance of a connection? The algorithm was simply asked to count the number of times the two names appeared in the text within fifteen words of each other. This doesn’t measure friendship – it indicates some measure of interaction or connection between them.

They decided to analyse the third volume in the series, A Storm of Swords, as the narrative had settled down by this point, and began by constructing a page rank analysis of the nodes or characters in the network. Three characters quickly stood out as important to the plot: Tyrion, Jon Snow and Sansa Stark. Anyone who has read the books or seen the series would not be surprised by this revelation. What is striking is that a computer algorithm which does not understand what it is reading achieved this same insight. It did so not simply by counting how many times a character’s name appears – that would pull out other names. It turned out that a subtler analysis of the network revealed the true protagonists.

To date, all three characters have survived Martin’s ruthless pen which has cut short some of the other key characters in the third volume. This is the mark of a good algorithm: it can be used in multiple scenarios. This one can tell you something useful from football to Game of Thrones.

Maths, the secret to a happy marriage

Sergey Brin and Larry Page may have cracked the code to steer you to websites you don’t even know you’re looking for, but can an algorithm really do something as personal as find your soulmate? Visit OKCupid and you’ll be greeted by a banner proudly declaring: ‘We use math to find you dates’.

These dating websites use a ‘matching algorithm’ to search through profiles and match people up according to their likes, dislikes and personality traits. They seem to be doing a pretty good job. In fact, the algorithms seem to be better than we are on our own: recent research published in the Proceedings of the National Academy of Sciences looked at 19,000 people who married between 2005 and 2012 and found that those who met online were happier and had more stable marriages.

The first algorithm to win its creators a Nobel Prize, originally formulated by two mathematicians, David Gale and Lloyd Shapley, in 1962, used a matching algorithm to solve something called ‘the Stable Marriage Problem’. Gale, who died in 2008, missed out on the award, but Shapley shared the prize in 2012 with the economist Alvin Roth, who saw the importance of the algorithm not just to the question of relationships but also to social problems including assigning health care and student places fairly.

Shapley was amused by the award: ‘I consider myself a mathematician and the award is for economics,’ he said at the time, clearly surprised by the committee’s decision. ‘I never, never in my life took a course in economics.’ But the mathematics he cooked up has had profound economic and social implications.

The Stable Marriage Problem that Shapley solved with Gale sounds more like a parlour game than a piece of cutting-edge economic theory. To illustrate the precise nature of the problem, imagine you’ve got four heterosexual men and four heterosexual women. They’ve been asked to list the four members of the opposite sex in order of preference. The challenge for the algorithm is to match them up in such a way as to come up with stable marriages. What this means is that there shouldn’t be a man and woman who would prefer to be with one another than with the partner they’ve been assigned. Otherwise there’s a good chance that at some point they’ll leave their partners to run off with one another. At first sight it isn’t at all clear, even with four pairs, that it is possible to arrange this.

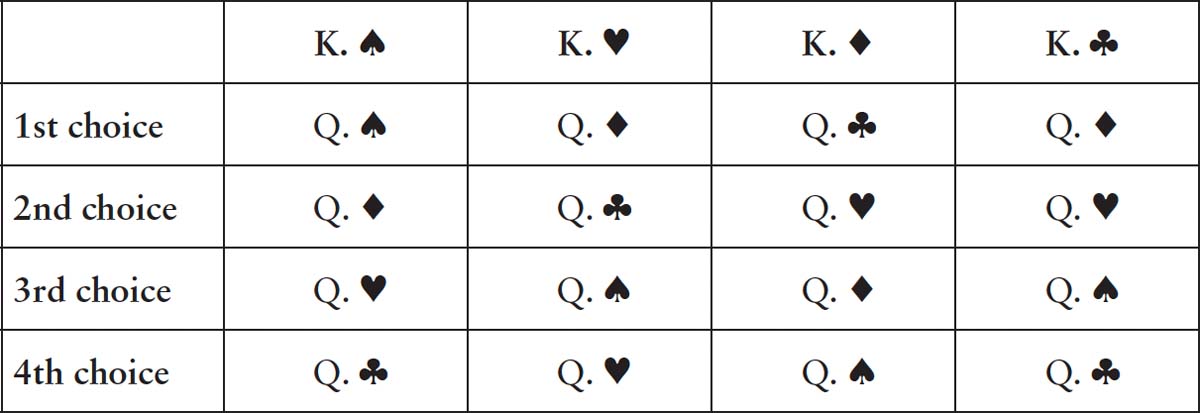
Let’s take a particular example and explore how Gale and Shapley could guarantee a stable pairing in a systematic and algorithmic manner. The four men will be played by the kings from a pack of cards: King of Spades, King of Hearts, King of Diamonds and King of Clubs. The women are the corresponding queens. Each king and queen has listed his or her preferences:

For the kings:

For the queens:

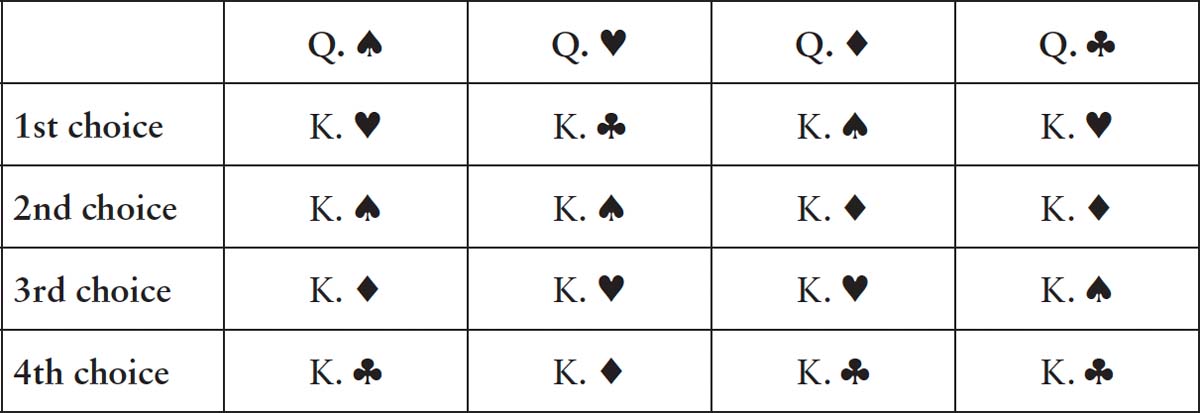
Now suppose you were to start by proposing that each king be paired with the queen of the same suit. Why would this result in an unstable pairing? The Queen of Clubs has ranked the King of Clubs as her least preferred partner so frankly she’d be happier with any of the other kings. And check out the King of Hearts’ list: the Queen of Hearts is at the bottom of his list. He’d certainly prefer the Queen of Clubs over the option he’s been given. In this scenario, we can envision the Queen of Clubs and the King of Hearts running away together. Matching kings and queens via their suits would lead to unstable marriages.

How do we match them so we won’t end up with two cards running off with each other? Here is the recipe Gale and Shapley cooked up. It consists of several rounds of proposals by the queens to the kings until a stable pairing finally emerges. In the first round of the algorithm, the queens all propose to their first choice. The Queen of Spades’ first choice is the King of Hearts. The Queen of Hearts’ first choice is the King of Clubs. The Queen of Diamonds chooses the King of Spades and the Queen of Clubs proposes to the King of Hearts. So it seems that the King of Hearts is the heart-throb of the pack, having received two proposals. He chooses which of the two queens he prefers, which is the Queen of Clubs, and rejects the Queen of Spades. So we have three provisional engagements, and one rejection.

First round

The rejected queen strikes off her first-choice king and in the next round moves on to propose to her second choice: the King of Spades. But now the King of Spades has two proposals. His first proposal from round one, the Queen of Diamonds, and a new proposal from the Queen of Spades. Looking at his ranking, he’d actually prefer the Queen of Spades. So he rather cruelly rejects the Queen of Diamonds (his provisional engagement on the first round of the algorithm).

Second round

Which brings us to round three. In each round, the rejected queens propose to the next king on their list and the kings always go for the best offer they receive. In this third round the rejected Queen of Diamonds proposes to the King of Diamonds (who has been standing like that kid who never gets picked for the team). Despite the fact that the Queen of Diamonds is low down on his list, he hasn’t got a better option, as the other three queens prefer other kings who have accepted them.

Third round

Finally everyone is paired up and all the marriages are stable. Although we have couched the algorithm in terms of a cute parlour game with kings and queens, the algorithm is now used all over the world: in Denmark to match children to day-care places; in Hungary to match students to schools; in New York to allocate rabbis to synagogues; and in China, Germany and Spain to match students to universities. In the UK it has been used by the National Health Service to match patients to organ donations, resulting in many lives being saved.

And it is building on top of the puzzle solved by Gale and Shapley that the modern algorithms which run our dating agencies are based. The problem is more complex since information is incomplete. Preferences are movable and relative, and shift even within relationships from day to day. But essentially the algorithms are trying to match people with preferences that will lead to a stable and happy pairing. And the evidence suggests that the algorithms could well be better than leaving it to human intuition.

You might have detected an interesting asymmetry in the algorithm that Gale and Shapley cooked up. We got the queens to propose to the kings. Would it have mattered if we had invited the kings to propose to the queens instead? Rather strikingly it does. You would end up with a different stable pairing if you applied the algorithm by swapping kings and queens.

The Queen of Diamonds would end up with the King of Hearts and the Queen of Clubs with the King of Diamonds. The two queens swap partners, but now they’re paired up with slightly lower choices. Although both pairings are stable, when queens propose to kings, the queens end up with the best pairings they could hope for. Flip things around and the kings are better off.

Medical students in America looking for residencies realised that hospitals were using this algorithm to assign places in such a way that the hospitals did the proposing. This meant the students were getting a worse deal. After some campaigning by students who pointed out how unfair this was, eventually the algorithm was reversed to give students the better end of the deal.

This is a powerful reminder that, as our lives are increasingly pushed around by algorithms, it’s important to understand how they work and what they’re doing, because otherwise you may be getting shafted.

The battle of the booksellers

The trouble with algorithms is that sometimes there are unexpected consequences. A human might be able to tell that something weird was happening, but an algorithm will just carry on doing what it was programmed to do, regardless of how absurd the consequences may be.

My favourite example of this centres on two second-hand booksellers who ran their shops using algorithms. A postdoc working at UC Berkeley was keen to get hold of a copy of Peter Lawrence’s book The Making of a Fly. It is a classic published in 1992 that developmental biologists often use, but by 2011 the text had been out of print for some time. The postdoc was after a second-hand copy.

Checking on Amazon, he found a number of copies priced at about $40, but then was rather shocked to see a copy on sale for $1,730,045.91. The seller, profnath, wasn’t even including shipping in the bargain. Then he noticed that there was another copy on sale for even more! This seller, bordeebook, was asking a staggering $2,198,177.95 (plus $3.99 for shipping of course).

The postdoc showed this to his supervisor, Michael Eisen, who presumed it must be a graduate student having fun. But both booksellers had very high ratings and seemed to be legitimate. Profnath had had over 8000 recommendations over the last twelve months, while bordeebook had had over 125,000 during the same period. Perhaps it was just a weird blip.

When Eisen checked the next day to see if the prices had dropped to more sensible levels, he found instead that they’d gone up. Profnath now wanted $2,194,443.04 while bordeebook was asking a phenomenal $2,788,233.00. Eisen decided to put his scientific hat on and analyse the data. Over the next few days he tracked the changes in an effort to work out if there was some pattern to the strange prices.

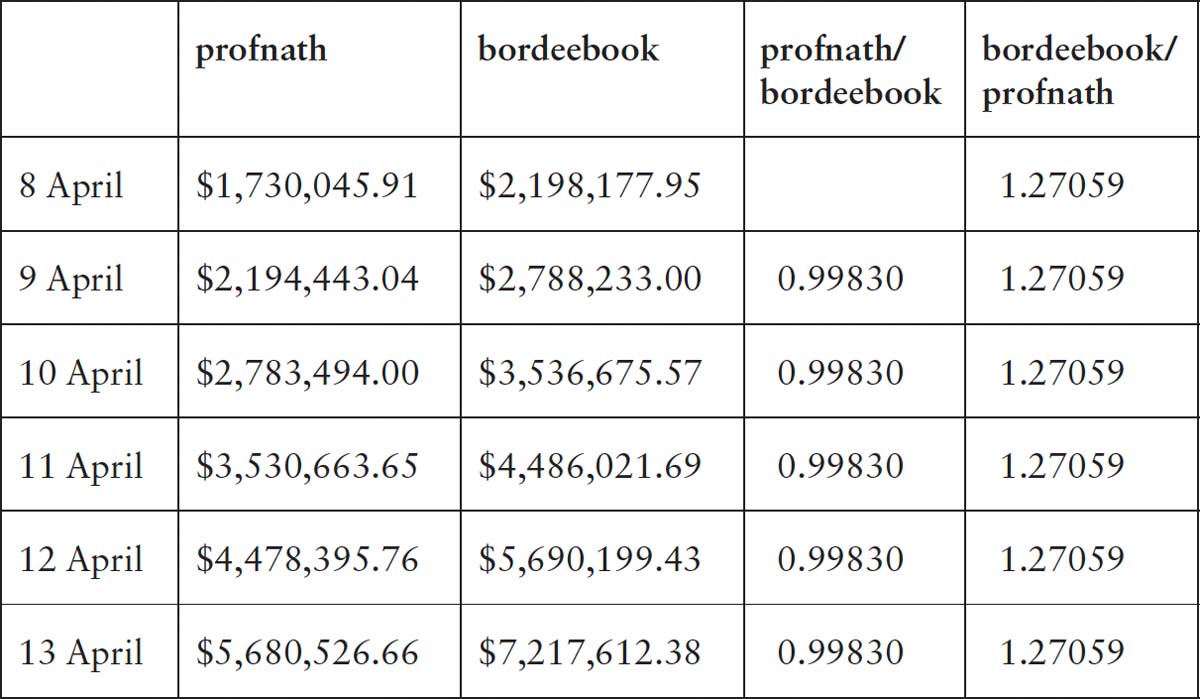
Eventually he spotted the mathematical rule behind the escalating prices. Divide the profnath price by the bordeebook price from the day before and you always got 0.99830. Divide the bordeebook price by the profnath book on the same day and you always got 1.27059. Each seller had programmed their website to use an algorithm that was setting the prices for books they were selling. Each day the profnath algorithm would check the price of the book at bordeebook and would then multiply it by 0.99830. This algorithm made perfect sense because the seller was programming the site to slightly undercut the competition at bordeebook. It is the algorithm at bordeebook that is slightly more curious. It was programmed to detect any price change in its rival and to multiply this new price by a factor of 1.27059.

The combined effect was that each day the price would be multiplied by 0.99830 × 1.27059, or 1.26843. This ensured that the price would grow exponentially. If profnath had set a sharper factor to undercut the price being offered by bordee-book, you would have seen the price collapse over time rather than escalate.

The explanation for profnath’s algorithm seems clear, but why was bordeebook’s algorithm set to offer the book at a higher price? Surely no one would buy the more expensive book? Perhaps they were relying on their bigger reputation with a greater number of positive recommendations to drive traffic their way, especially if their price was only slightly higher, which at the start it would have been. As Eisen wrote in his blog, ‘this seems like a fairly risky thing to rely on. Meanwhile you’ve got a book sitting on the shelf collecting dust. Unless, of course, you don’t actually have the book …’

Then the truth suddenly dawned on him. Of course. They didn’t actually have the book! The algorithm was programmed to see what books were out there and to offer the same book at a slight markup. If someone wanted the book from their reliable bordeebook’s website, then bordeebook would go and purchase it from the other bookseller and sell it on. But to cover costs this would necessitate a bit of a markup. The algorithm thus multiplied the price by a factor of 1.27059 to cover the purchase of the book, the shipping and a little extra profit.

Using a few logarithms it’s possible to work out that the book most likely first went on sale forty-five days before 8 April at about $40. This shows the power of exponential growth. It only took a month and a half for the price to reach into the millions! The price peaked at $23,698,655.93 (plus $3.99 shipping) on 18 April, when finally a human at profnath intervened, realising that something strange was going on. The price then dropped to $106.23. Predictably bordeebook’s algorithm offered their book at $106.23 × 1.27059 = $134.97.

The mispricing of The Making of a Fly did not have a devastating impact for anyone involved, but there are more serious cases of algorithms used to price stock options causing flash crashes on the markets. The unintended consequences of algorithms is one of the prime sources of the existential fears people have about advancing technology. What if a company builds an algorithm that is tasked with maximising the collection of carbon, but it suddenly realises the humans who work in the factory are carbon-based organisms, so it starts harvesting the humans in the factory for carbon production? Who would stop it?

Algorithms are based on mathematics. At some level they are mathematics in action. But they don’t really creatively stretch the field. No one in the mathematical community feels particularly threatened by them. We don’t really believe that algorithms will turn on their creators and put us out of a job. For years I believed that these algorithms would do no more than speed up the mundane part of my work. They were just more sophisticated versions of Babbage’s calculating machine that could be told to do the algebraic or numerical manipulations which would take me tedious hours to write out by hand. I always felt in control. But that is all about to change.

Up till a few years ago it was felt that humans understood what their algorithms were doing and how they were doing it. Like Lovelace, they believed you couldn’t really get more out than you put in. But then a new sort of algorithm began to emerge, an algorithm that could adapt and change as it interacted with its data. After a while its programmer may not understand quite why it is making the choices it is. These programs were starting to produce surprises, and for once you could get more out than you put in. They were beginning to be more creative. These were the algorithms DeepMind exploited in its crushing of humanity in the game of Go. They ushered in the new age of machine learning.

5

FROM TOP DOWN TO BOTTOM UP

Machines take me by surprise with great frequency.

Alan Turing

I first met Demis Hassabis a few years before his great Go triumph at a meeting about the future of innovation. New companies were on the lookout for investment from venture capitalists and investors. Some were going to transform the future, but most would flash and burn. The art was for VCs and angel investors to spot the winners. I must admit when I heard Hassabis speak about code that could learn, adapt and improve I dismissed him out of hand. I couldn’t see how, if you were programming a computer to play a game, the program could get any further than the person who was writing the code. How could you get more out than you were putting in? I wasn’t the only one. Hassabis admits that getting investors to give money to AI a decade ago was extremely difficult.

How I wish now that I’d backed that horse as it came trotting by! The transformative impact of the ideas Hassabis was proposing can be judged by the title of a recent session on AI: ‘Is machine learning the new 42?’ (The allusion to Douglas Adams’s answer to the question of life, the universe and everything from his book The Hitchhiker’s Guide to the Galaxy would have been familiar to the geeky attendees, many of whom were brought up on a diet of sci-fi.) So what has happened to spark this new AI revolution?

The simple answer is data. It is an extraordinary fact that 90 per cent of the world’s data has been created in the last five years. 1 exabyte (10) of data is created on the internet every day, roughly the equivalent of the amount of data that can be stored on 250 million DVDs. Humankind now produces in two days the same amount of data it took us from the dawn of civilisation until 2003 to generate.