The Creativity Code: How AI is learning to write, paint and think

It certainly seemed to. AlphaGo appeared to completely ignore the play, responding with a strange move. Within several more moves AlphaGo could see that it was losing. The DeepMind team stared at their screens behind the scenes and watched their creation imploding. It was as if move 78 short-circuited the program. It seemed to cause AlphaGo to go into meltdown as it made a whole sequence of destructive moves. This apparently is another characteristic of the way Go algorithms are programmed. Once they see that they are losing they go rather crazy.

Silver, the chief programmer, winced as he saw the next move AlphaGo was suggesting: ‘I think they’re going to laugh.’ Sure enough, the Korean commentators collapsed into fits of giggles at the moves AlphaGo was now making. Its moves were failing the Turing Test. No human with a shred of strategic sense would make them. The game dragged on for a total of 180 moves, at which point AlphaGo put up a message on the screen that it had resigned. The press room erupted with spontaneous applause.

The human race had got one back. AlphaGo 3 Humans 1. The smile on Lee Sedol’s face at the press conference that evening said it all. ‘This win is so valuable that I wouldn’t exchange it for anything in the world.’ The press cheered wildly. ‘It’s because of the cheers and the encouragement that you all have shown me.’

Gu Li, who was commentating on the game in China, declared Sedol’s move 78 as the ‘hand of god’. It was a move that broke the conventional way to play the game and that was ultimately the key to its shocking impact. Yet this is characteristic of true human creativity. It is a good example of Boden’s transformational creativity, whereby breaking out of the system you can find new insights.

At the press conference, Hassabis and Silver could not explain why AlphaGo had lost. They would need to go back and analyse why it had made such a lousy move in response to Sedol’s move 78. It turned out that AlphaGo’s experience in playing humans had led it to totally dismiss such a move as something not worth thinking about. It had assessed that this was a move that had only a one in 10,000 chance of being played. It seems as if it just had not bothered to learn a response to such a move because it had prioritised other moves as more likely and therefore more worthy of response.

Perhaps Sedol just needed to get to know his opponent. Perhaps over a longer match he would have turned the tables on AlphaGo. Could he maintain the momentum into the fifth and final game? Losing 3–2 would be very different from 4–1. The last game was still worth competing in. If he could win a second game, then it would sow seeds of doubt about whether AlphaGo could sustain its superiority.

But AlphaGo had learned something valuable from its loss. You play Sedol’s one in 10,000 move now against the algorithm and you won’t get away with it. That’s the power of this sort of algorithm. It learns from its mistakes.

That’s not to say it can’t make new mistakes. As game 5 proceeded, there was a moment quite early on when AlphaGo seemed to completely miss a standard set of moves in response to a particular configuration that was building. As Hassabis tweeted from backstage: ‘#AlphaGo made a bad mistake early in the game (it didn’t know a known tesuji) but now it is trying hard to claw it back … nail-biting.’

Sedol was in the lead at this stage. It was game on. Gradually AlphaGo did claw back. But right up to the end the DeepMind team was not exactly sure whether it was winning. Finally, on move 281 – after five hours of play – Sedol resigned. This time there were cheers backstage. Hassabis punched the air. Hugs and high fives were shared across the team. The win that Sedol had pulled off in game 4 had suddenly re-engaged their competitive spirit. It was important for them not to lose this last game.

Looking back at the match, many recognise what an extraordinary moment this was. Some immediately commented on its being an inflexion point for AI. Sure, all this machine could do was play a board game, and yet, for those looking on, its capability to learn and adapt was something quite new. Hassabis’s tweet after winning the first game summed up the achievement: ‘#AlphaGo WINS!!!! We landed it on the moon.’ It was a good comparison. Landing on the moon did not yield extraordinary new insights about the universe, but the technology that we developed to achieve such a feat has. Following the last game, AlphaGo was awarded an honorary professional 9 dan rank by the South Korean Go Association, the highest accolade for a Go player.

From hilltop to mountain peak

Move 37 of game 2 was a truly creative act. It was novel, certainly, it caused surprise, and as the game evolved it proved its value. This was exploratory creativity, pushing the limits of the game to the extreme.

One of the important points about the game of Go is that there is an objective way to test whether a novel move has value. Anyone can come up with a new move that appears creative. The art and challenge are in making a novel move that has some sort of value. How should we assess value? It can be very subjective and time-dependent. Something that is panned critically at the time of its release can be recognised generations later as a transformative creative act. Nineteenth-century audiences didn’t know what to make of Beethoven’s Symphony no. 5, and yet it is central repertoire now. During his lifetime Van Gogh could barely sell his paintings, trading them for food or painting materials, but now they go for millions. In Go there is a more tangible and immediate test of value: does it help you win the game? Move 37 won AlphaGo game 2. There was an objective measure that we could use to value the novelty of this move.

AlphaGo had taught the world a new way to play an ancient game. Analysis since the match has resulted in new tactics. The fifth line is now played early on, as we have come to understand that it can have big implications for the endgame. AlphaGo has gone on to discover still more innovative strategies. DeepMind revealed at the beginning of 2017 that its latest iteration had played online anonymously against a range of top-ranking professionals under two pseudonyms: Master and Magister. Human players were unaware that they were playing a machine. Over a few weeks it had played a total of sixty complete games. It won all sixty games.

But it was the analysis of the games that was truly insightful. Those games are now regarded as a treasure trove of new ideas. In several games AlphaGo played moves that beginners would have their wrists slapped for by their Go master. Traditionally you do not play a stone in the intersection of the third column and third row. And yet AlphaGo showed how to use such a move to your advantage.

Hassabis describes how the game of Go had got stuck on what mathematicians like to call a local maximum. If you look at the landscape I’ve drawn here then you might be at the top of peak A. From this height there is nowhere higher to go. This is called a local maximum. If there were fog all around you, you’d think you were at the highest point in the land. But across the valley is a higher peak. To know this, you need the fog to clear. You need to descend from your peak, cross the valley and climb the higher peak.

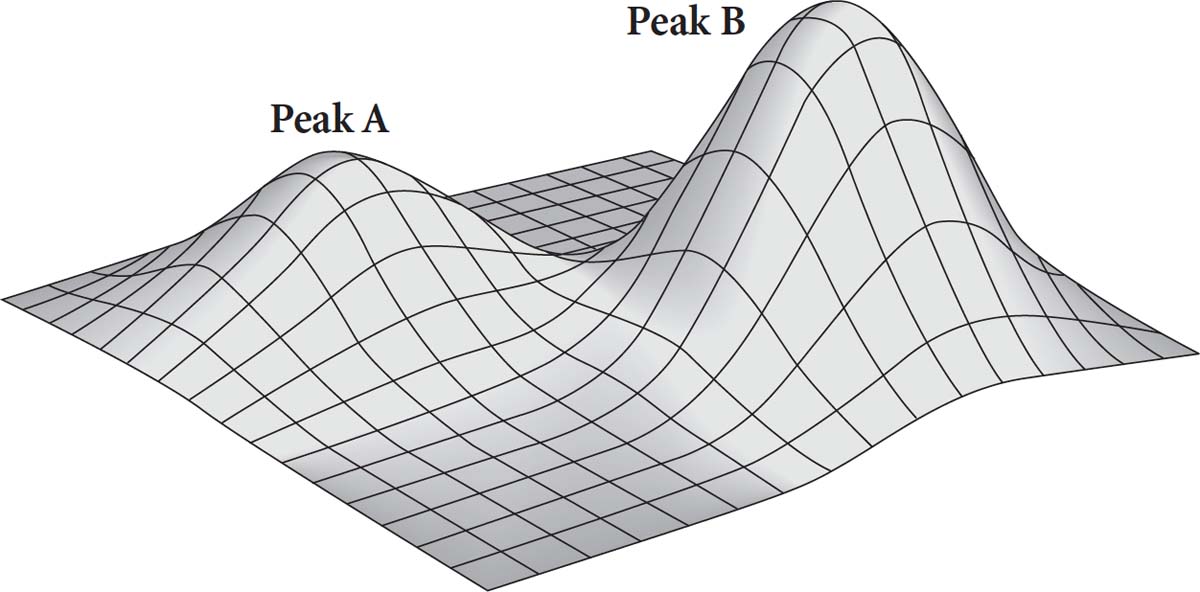
The trouble with modern Go is that conventions had built up about ways to play that had ensured players hit peak A. But by breaking those conventions AlphaGo had cleared the fog and revealed an even higher peak B. It’s even possible to measure the difference. In Go, a player using the conventions of peak A will in general lose by two stones to the player using the new strategies discovered by AlphaGo.

This rewriting of the conventions of how to play Go has happened at a number of previous points in history. The most recent was the innovative game play introduced by the legendary Go Seigen in the 1930s. His experimentation with ways of playing the opening moves revolutionised the way the game is played. But Go players now recognise that AlphaGo might well have launched an even greater revolution.

The Chinese Go champion Ke Jie recognises that we are in a new era: ‘Humanity has played Go for thousands of years, and yet, as AI has shown us, we have not yet even scratched the surface. The union of human and computer players will usher in a new era.’

Ke Jie’s compatriot Gu Li, winner of the most Go world titles, added: ‘Together, humans and AI will soon uncover the deeper mysteries of Go.’ Hassabis compares the algorithm to the Hubble telescope. This illustrates the way many view this new AI. It is a tool for exploring deeper, further, wider than ever before. It is not meant to replace human creativity but to augment it.

And yet there is something that I find quite depressing about this moment. It feels almost pointless to want to aspire to be the world champion at Go when you know there is a machine that you will never be able to beat. Professional Go players have tried to put a brave face on it, talking about the extra creativity that it has unleashed in their own play, but there is something quite soul-destroying about knowing that we are now second best to the machine. Sure, the machine was programmed by humans, but that doesn’t really seem to make it feel better.

AlphaGo has since retired from competitive play. The Go team at DeepMind has been disbanded. Hassabis proved his Cambridge lecturer wrong. DeepMind has now set its sights on other goals: health care, climate change, energy efficiency, speech recognition and generation, computer vision. It’s all getting very serious.

Given that Go was always my shield against computers doing mathematics, was my own subject next in DeepMind’s cross hairs? To truly judge the potential of this new AI we are going to need to look more closely at how it works and dig around inside. The crazy thing is that the tools DeepMind is using to create the programs that might put me out of a job are precisely the ones that mathematicians have created over the centuries. Is this mathematical Frankenstein’s monster about to turn on its creator?

4

ALGORITHMS, THE SECRET TO MODERN LIFE

The Analytical Engine weaves algebraic patterns, just as the Jacquard loom weaves flowers and leaves.

Ada Lovelace

Our lives are completely run by algorithms. Every time we search for something on the internet, plan a journey with our GPS, choose a movie recommended by Netflix or pick a date online, we are being guided by an algorithm. Algorithms are steering us through the digital age, yet few people realise that they predate the computer by thousands of years and go to the heart of what mathematics is all about.

The birth of mathematics in Ancient Greece coincides with the development of one of the very first algorithms. In Euclid’s Elements, alongside the proof that there are infinitely many prime numbers, we find a recipe that, if followed step by step, solves the following problem: given two numbers, find the largest number that divides them both.

It may help to put the problem in more visual terms. Imagine that the floor of your kitchen is 36 feet long by 15 feet wide. You want to know the largest square tile that will enable you to cover the entire floor without cutting any tiles. So what should you do? Here is the 2000-year-old algorithm that solves the problem:

Suppose you have two numbers, M and N (and suppose N is smaller than M). Start by dividing M by N and call the remainder N1. If N1 is zero, then N is the largest number that divides them both. If N1 is not zero, then divide N by N1 and call the remainder N2. If N2 is zero, then N1 is the largest number that divides M and N. If N2 is not zero, then do the same thing again. Divide N1 by N2 and call the remainder N3. These remainders are getting smaller and smaller and are whole numbers, so at some point one must hit zero. When it does, the algorithm guarantees that the previous remainder is the largest number that divides both M and N. This number is known as the highest common factor or greatest common divisor.

Now let’s return to our challenge of tiling the kitchen floor. First we find the largest square tile that will fit inside the original shape. Then we look for the largest square tile that will fit inside the remaining part – and so on, until you hit a square tile that finally covers the remaining space evenly. This is the largest square tile that will enable you to cover the entire floor without cutting any tiles.

If M = 36 and N = 15, then dividing N into M gives you a remainder of N1 = 6. Dividing N1 into N we get a remainder of N2 = 3. But now dividing N1 by N2 we get no remainder at all, so we know that 3 is the largest number that can divide both 36 and 15.

You see that there are lots of ‘if …, then …’ clauses in this process. That is typical of an algorithm and is what makes algorithms so perfect for coding and computers. Euclid’s ancient recipe gets to the heart of four key characteristics any algorithm should ideally possess:

 1. It should consist of a precisely stated and unambiguous set of instructions.

 2. The procedure should always finish, regardless of the numbers you insert. (It should not enter an infinite loop!)

 3. It should give the answer for any values input into the algorithm.

 4. Ideally it should be fast.

In the case of Euclid’s algorithm, there is no ambiguity at any stage. Because the remainder grows smaller at every step, after a finite number of steps it must hit zero, at which point the algorithm stops and spits out the answer. The bigger the numbers, the longer the algorithm will take, but it’s still proportionally fast. (The number of steps is five times the number of digits in the smaller of the two numbers, for those who are curious.)

If one of the oldest algorithms is 2000 years old then why does it owe its name to a ninth-century Persian mathematician? Muhammad Al-Khwarizmi was one of the first directors of the great House of Wisdom in Baghdad and was responsible for many of the translations of the Ancient Greek mathematical texts into Arabic. ‘Algorithm’ is the Latin interpretation of his name. Although all the instructions for Euclid’s algorithm are there in the Elements, the language that Euclid used was very clumsy. The Ancient Greeks thought very geometrically, so numbers were lengths of lines and proofs consisted of pictures – a bit like our example with tiling the kitchen floor. But pictures are not a rigorous way to do mathematics. For that you need the language of algebra, where a letter can stand for any number. This was the invention of Al-Khwarizmi.

To be able to articulate clearly how an algorithm works you need a language that allows you to talk about a number without specifying what that number is. We already saw it at work in explaining how Euclid’s algorithm worked. We gave names to the numbers that we were trying to analyse: N and M. These variables can represent any number. The power of this new linguistic take on mathematics meant that it allowed mathematicians to understand the grammar that underlies the way that numbers work. You didn’t have to talk about particular examples where the method worked. This new language of algebra provided a way to explain the patterns that lie behind the behaviour of numbers. A bit like a code for running a program, it shows why it would work whatever numbers you chose, the third criterion in our conditions for a good algorithm.

Algorithms have become the currency of our era because they are perfect fodder for computers. An algorithm exploits the pattern underlying the way we solve a problem to guide us to a solution. The computer doesn’t need to think. It just follows the instructions encoded in the algorithm again and again, and, as if by magic, out pops the answer you were looking for.

Desert island algorithm

One of the most extraordinary algorithms of the modern age is the one that helps millions of us navigate the internet every day. If I were cast away on a desert island and could only take one algorithm with me, I’d probably choose the one that drives Google. (Not that it would be much use, as I’d be unlikely to have an internet connection.)

In the early days of the internet (we’re talking the early 1990s) there was a directory that listed all of the existing websites. In 1994 there were only 3000 of them. The internet was small enough for you to pretty easily thumb through and find what you were looking for. Things have changed quite a bit since then. When I started writing this paragraph there were 1,267,084,131 websites live on the internet. A few sentences later that number has gone up to 1,267,085,440. (You can check the current status here: http://www.internetlivestats.com/.)

How does Google figure out exactly which one of the billion websites to recommend? Mary Ashwood, an 86-year-old granny from Wigan, was careful to send her requests with a courteous ‘please’ and ‘thank you’, perhaps imagining an industrious group of interns on the other end sifting through the endless requests. When her grandson Ben opened her laptop and found ‘Please translate these roman numerals mcmxcviii thank you’, he couldn’t resist tweeting the world about his nan’s misconception. He got a shock when someone at Google replied with the following tweet:

Dearest Ben’s Nan.

Hope you’re well.

In a world of billions of Searches, yours made us smile.

Oh, and it’s 1998.

Thank YOU

Ben’s Nan brought out the human in Google on this occasion, but there is no way any company could respond personally to the million searches Google receives every fifteen seconds. So if it isn’t magic Google elves scouring the internet, how does Google succeed in so spectacularly locating the answers you want?

It all comes down to the power and beauty of the algorithm Larry Page and Sergey Brin cooked up in their dorm rooms at Stanford in 1996. They originally wanted to call their new algorithm ‘Backrub’, but eventually settled instead on ‘Google’, inspired by the mathematical number for one followed by 100 zeros, which is known as a googol. Their mission was to find a way to rank pages on the internet to help navigate this growing database, so a huge number seemed like a cool name.

It isn’t that there weren’t other algorithms out there being used to do the same thing, but these were pretty simple in their conception. If you wanted to find out more about ‘the polite granny and Google’, existing algorithms would have identified all of the pages with these words and listed them in order, putting the websites with the most occurrences of the search terms up at the top.

That’s OK but easily hackable: any florist who sticks into their webpage’s meta-data the words ‘Mother’s Day Flowers’ a thousand times will shoot to the top of every son or daughter’s search. You want a search engine that can’t easily be pushed around by savvy web designers. So how can you come up with an unbiased measure of the importance of a website? And how can you find out which sites you can ignore?

Page and Brin struck on the clever idea that if a website has many links pointing to it, then those other sites are signalling that it is worth visiting. The idea is to democratise the measure of a website’s worth by letting other websites vote for who they think is important. But, again, this could be hacked. I just need to set up a thousand artificial websites linking to my florist’s website and it will bump the site up the list. To prevent this, they decided to give more weight to a vote that came from a website that itself commanded respect.

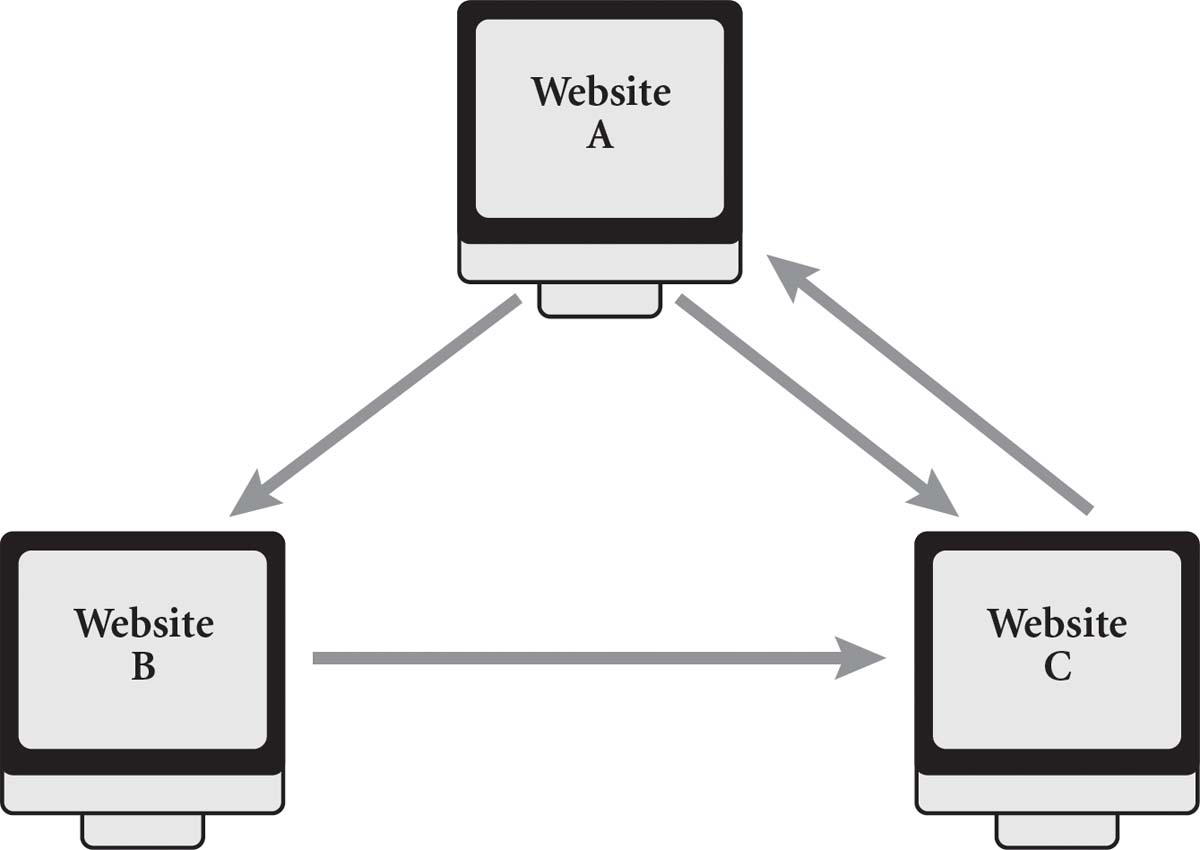
This still left them with a challenge: how do you rank the importance of one site over another? Take this mini-network as an example.

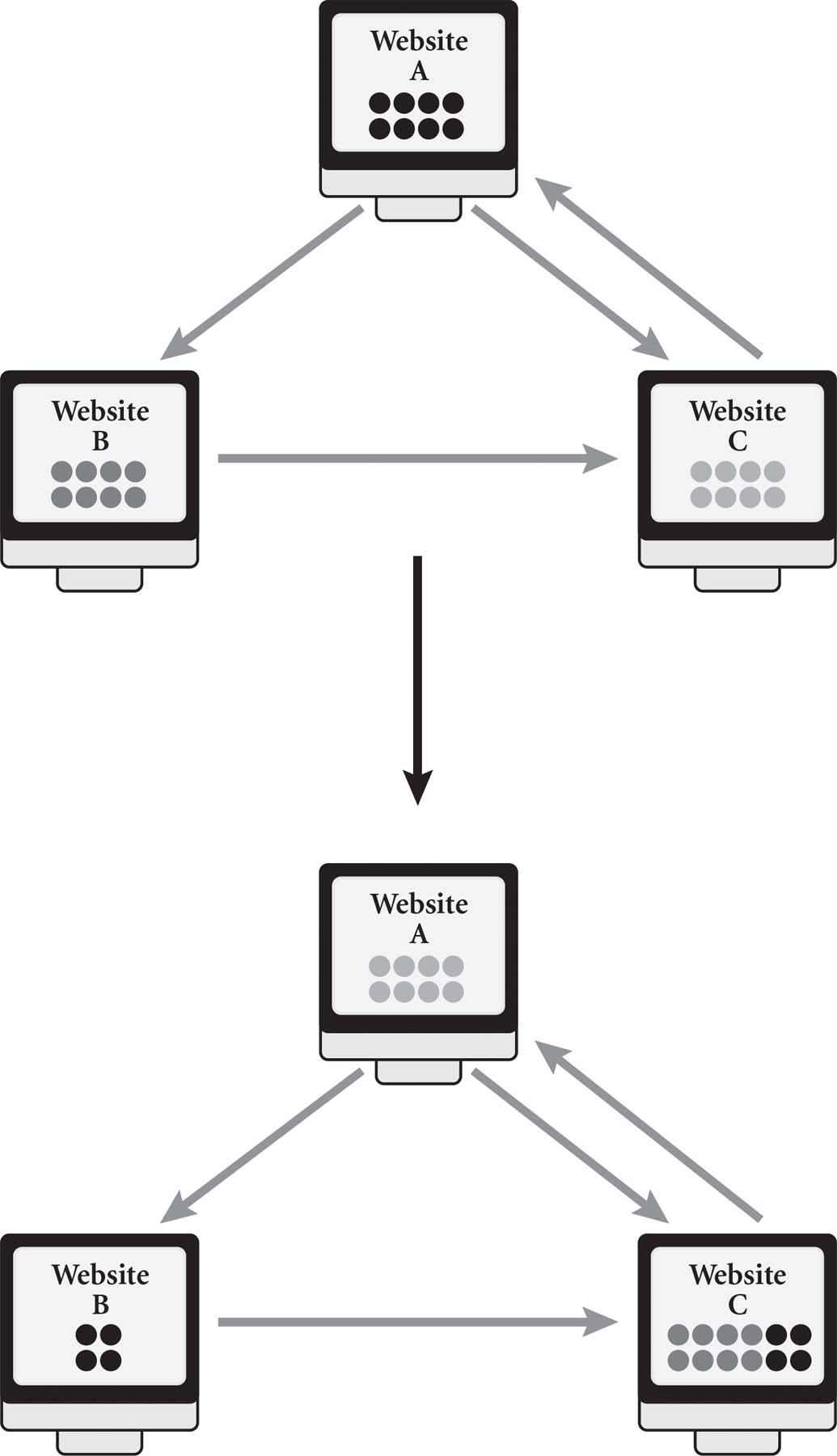
We want to start by giving each site equal weight. Let’s think of the websites as buckets; we’ll give each site eight balls to indicate that they have equal rank. Now the websites have to give their balls to the sites they link to. If they link to more than one site, then they will share their balls equally. Since website A links to both website B and website C, for example, it will give 4 balls to each site. Website B, however, has decided to link only to website C, putting all eight of its balls into website C’s bucket.

After the first distribution, website C comes out looking very strong. But we need to keep repeating the process because website A will be boosted by the fact that it is being linked to by the now high-ranking website C. The table below shows how the balls move around as we iterate the process.

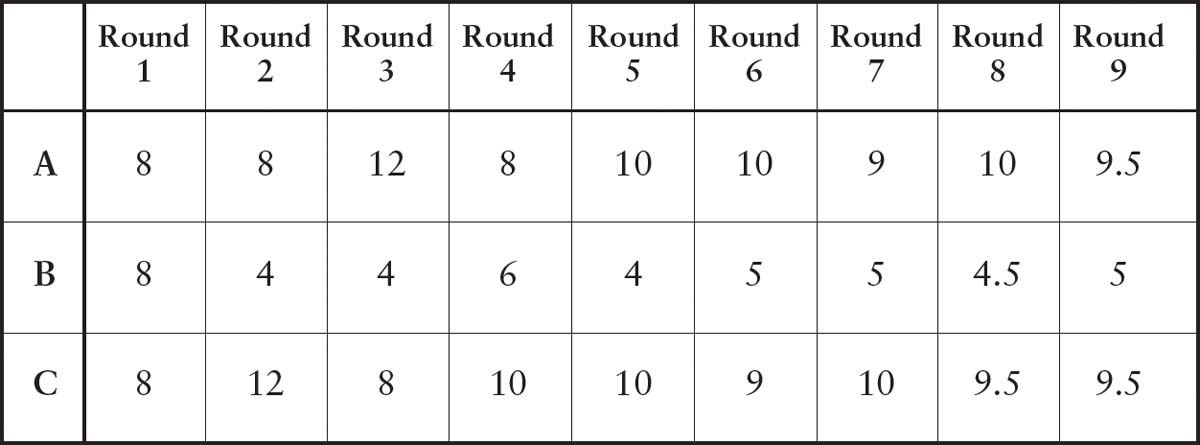
At the moment, this does not seem to be a particularly good algorithm. It appears not to stabilise and is rather inefficient, failing two of our criteria for the ideal algorithm. Page and Brin’s great insight was to realise that they needed to find a way to assign the balls by looking at the connectivity of the network. It turned out they’d been taught a clever trick in their university mathematics course that worked out the correct distribution in one step.

The trick starts by constructing a matrix which records the way that the balls are redistributed among the websites. The first column of the matrix records the proportion going from website A to the other websites. In this case 0.5 goes to website B and 0.5 to website C. The matrix of redistribution is therefore given by the following matrix:

The challenge is to find what is called the eigenvector of this matrix with eigenvalue 1. This is a column vector that does not get changed when multiplied by the matrix.1 Finding these eigenvectors or stability points is something we teach undergraduates early on in their university career. In the case of our network we find that the following column vector is stabilised by the redistribution matrix:

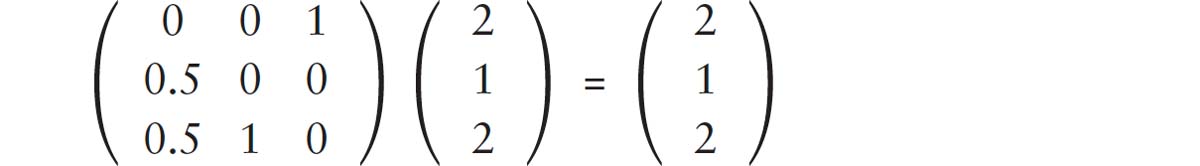
This means that if we split the balls in a 2:1:2 distribution we see that this weighting is stable. Distribute the balls using our previous game and the sites still have a 2:1:2 distribution.

Eigenvectors of matrices are an incredibly potent tool in mathematics and the sciences more generally. They are the secret to working out the energy levels of particles in quantum physics. They can tell you the stability of a rotating fluid like a spinning star or the reproduction rate of a virus. They may even be key to understanding how prime numbers are distributed throughout all numbers.

By calculating the eigenvector of the network’s connectivity we see that websites A and C should be ranked equally. Although website A is linked to by only one site (website C), the fact that website C is highly valued and links only to website A means that its link bestows high value to website A.