Искусственный интеллект в лучевой диагностике: Per Aspera Ad Astra

Известный афоризм гласит, что данные – это топливо для искусственного интеллекта. Однако объемы этого топлива отнюдь не безграничны. В реальной практике разработки, тестирования и эксплуатации СИИ необходимы обоснованные подходы для оценки размеров наборов данных.

Согласно ГОСТ Р 59921.5—2022 размер выборки для обучения или тестирования СИИ определяется целью его применения и зависит от следующих факторов99:

– требуемое качество решений СИИ;

– тип и архитектура алгоритма СИИ;

– количество параметров алгоритма СИИ;

– качество данных, включая качество аннотаций, распределение метрик и уровень шума в наборе данных.

В данном контексте необходимо упомянуть такую характеристику набора данных, как размерность. Под ней понимают количество атрибутов, которые имеют объекты в НД (например, диаметр магистрального сосуда, объем кровоизлияния, значение артериального давления и др.). Высокая размерность выдвигает повышенные требования к алгоритмам СИИ, допустимому размеру НД, а также к вычислительным ресурсам для их обработки. В ряде случаев допустимо обоснованное снижение размерности НД, в частности за счет кластеризации данных либо группировки взаимосвязанных по какому-либо признаку атрибутов в объединенные категории100.

Длительное время обоснования оценки необходимого и достаточного размера набора данных (НД) для обучения и тестирования СИИ находились на стадии разработки. Применялись автоматизированные средства расчета на основе ширины 95% доверительного интервала и допустимой ширины определения метрик. Известен эмпирический метод, согласно которому размер набора данных должен в несколько раз превышать количество параметров алгоритма СИИ либо соответствовать другим обоснованным критериям. Такая ситуация не соответствовала уровню качества научных исследований, установленному для Московского эксперимента, поэтому были проведены оригинальные изыскания для обоснования и создания объективных методов определения размера набора данных.

2.3.2. Статистические подходы для известной доли значений качественного признака (цитируется по оригинальной статье авторов101)

Первые предложенные в рамках Московского эксперимента подходы к формированию выборки применялись к НД, используемым для мониторинга (ретроспективного контроля качества результатов работы ИИ-сервисов). Они соответствовали принципам математической статистики и основывались на известной вероятности технологического дефекта в генеральной совокупности, равной 10%. Объем генеральной совокупности при этом принимался в пределах от 1000 до 100 000 исследований102.

В рамках следующих подходов проводилась серийная бесповторная выборка, которая характеризовалась тем, что выбранная единица отбиралась из всего объема генеральной совокупности и не возвращалась обратно.

1. Подход, основанный на точечной статистической оценке. Данный подход учитывает отклонение результатов выборочного исследования от генеральных значений (2.1):

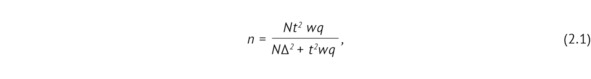
где n – объем выборки; N – объем генеральной совокупности; t – коэффициент, показывающий, с какой вероятностью (надежностью) можно гарантировать достоверность полученного результата или критическое значение критерия Стьюдента при соответствующем уровне значимости (для уровня значимости 0,05 коэффициент); Δ – предельная ошибка показателя; w – доля изучаемого признака; q = (1 – w) – доля, где изучаемый признак отсутствует.

Таким образом, при доле изучаемого признака (w) 0,9, уровне статистической значимости 0,95 и предельно допустимой ошибке (Δ) 0,05 был получен объем выборки (n), равный 138.

2. Подход, основанный на проверке статистических гипотез (вариант 1). Подход предполагает проверку статистической гипотезы H0 (исследования формируемого НД удовлетворяют предъявляемым требованиям) при наличии альтернативной гипотезы H1 (исследования формируемого НД не соответствуют предъявляемым требованиям). Если среди исследований число дефектных (m) не превышает приемочное число (m ≤ с) (максимально допустимое количество технических дефектов среди выборки), то НД принимается; в противном случае – бракуется. Для выбора плана контроля (определения выборки) используется формула (2.2):

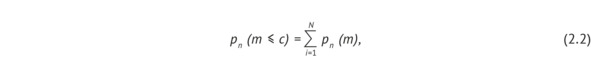
где m – число дефектных единиц продукции в выборке n; pn (m) – вероятность появления дефектных единиц продукции m в выборке n; c – приемочное число.

Так как в рамках Московского эксперимента объем генеральной совокупности превышал объем выборки более чем на 10%, то оперативные характеристики определяли по формуле (2.3):

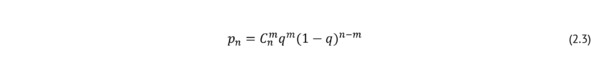
где Cnm – количество сочетаний появления дефектных единиц продукции m в выборке n (2.4):

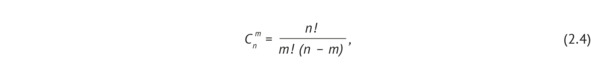
На примере Московского эксперимента было использовано приемочное число, равное двум единицам продукции, произведены расчеты и построены кривые для выборок в 30, 50, 80, 138 единиц продукции. На рисунке 2.18 обозначены следующие риски:

– вероятность отклонить генеральную совокупность исследований при ее хорошем качестве (т.е. в генеральной совокупности удельный вес дефектных единиц продукции менее 10%) – учитывая долю заявленных дефектных исследований от ИИ-сервиса, риск принимаем равным 1%;

– вероятность принять генеральную совокупность при ее низком качестве – учитывая долю дефектных изделий, определенных валидатором ПО с ТИИ (в данном случае – валидатором является ГБУЗ НПКЦ ДиТ ДЗМ), риск принимаем равным 10%.

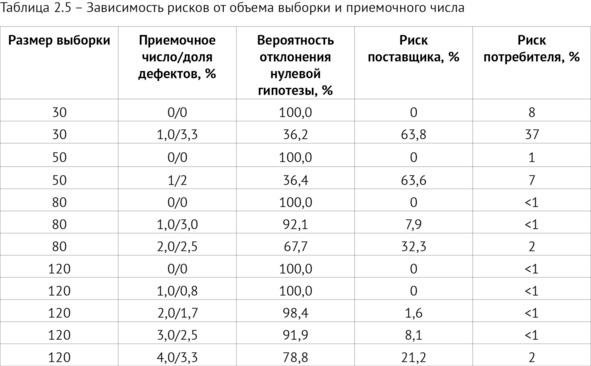
Анализируя данные таблицы 2.5 и учитывая описанные выше риски на уровне не более 10% и не более 5% соответственно, установили, что объем выборки, равный 80, удовлетворяет требованиям как со стороны ИИ-сервиса, так и валидатора.

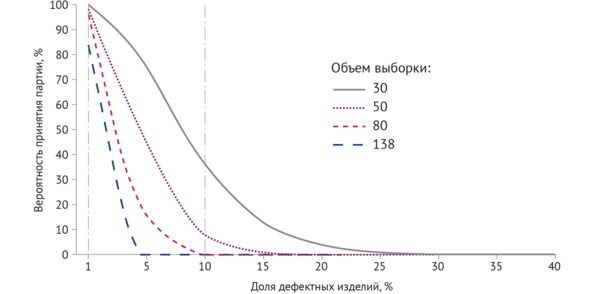
Рисунок 2.18 – Оперативная характеристика для различных объемов выборки: вертикальная штрихпунктирная линия с двумя точками – риск ИИ-сервиса; вертикальная штрихпунктирная линия с одной точкой – риск валидатора

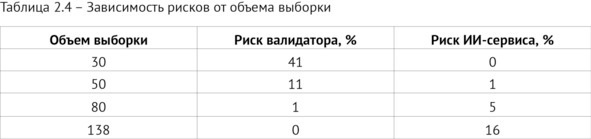
3. Подход, основанный на проверке статистических гипотез (вариант 2). Данный подход базируется на принципах вероятности отклонения нулевой гипотезы; учитывает риски обеих сторон. Нулевая гипотеза H0 предполагает, что если в генеральной совокупности содержится более 10% дефектных исследований, то генеральная совокупность за отчетный период содержит более 10% исследований с технологическими дефектами. Соответственно, при альтернативной гипотезе H1 – менее 10% исследований с технологическими дефектами. Вероятность отклонения нулевой гипотезы – не менее 80%.

Выполнены расчеты (таблица 2.5) для выборок в 30, 50, 80, 120 исследований с приемочным числом от нуля до четырех (приемочное число ограничивалось превышением рисков валидатора более 10% или ИИ-сервиса – более 5%).

Анализируя данные таблицы 2.6 и учитывая заданные риски, а также долю заявленных дефектных исследований от ИИ-сервиса (1%) и долю дефектных исследований, определенных валидатором (10%), установили, что объем выборки, равный 30, 50, 80 и 120 единиц продукции, удовлетворяет требованиям обеих сторон при приемочном числе, равном нулю. С учетом доли дефектных исследований при приемочных числах больше нуля наиболее подходящие объемы выборок равнялись 80 или 120 единицам.

4. Подход, основанный на применении ГОСТ Р ИСО 2859-1-2007. ГОСТ Р ИСО 2859-1-2007 «Статистические методы, процедуры выборочного контроля по альтернативному признаку» устанавливает процедуру выборочного контроля по альтернативному признаку для штучной продукции на основе приемлемого уровня качества. Приемлемый уровень качества выражается в проценте несоответствующих единиц продукции или числе несоответствий на сто единиц продукции. Было рассмотрено несколько вариантов формирования объемов выборок. Сначала была использована таблица «Коды объема выборки» из указанного ГОСТ Р. В рассматриваемом случае общий уровень контроля равен II, специальный уровень контроля не используется. Так как объемы генеральной совокупности (партии в контексте ГОСТ Р) находились в пределах от 1000 до 100 000, то интерес представляли следующие коды: J, K, L, M. В то же время план не имел многоступенчатости и не подразумевал переход на ослабленный или усиленный контроль. В связи с этим были использованы данные из таблицы «Одноступенчатые планы при нормальном контроле (основная таблица)»: для приемлемого уровня качества потребителя в 10% (для партий объемом от 501 до 10 000 исследований) объем выборки для контроля качества будет равен 125 единицам продукции с приемочным числом партии, равным нулю; для партий объемом от 10 001 до 150 000 объем выборки для контроля качества будет равен 500 единицам продукции с приемочным числом партии, равным единице. При обращении к таблице «Риск изготовителя при нормальном контроле (процент непринятых партий для одноступенчатых планов)» были получены риски поставщика 11,8% для выборки в 125 единиц продукции; 9,02% – для выборки в 500 единиц.

В таблице 2.6 приведена сводная информация о сильных и слабых сторонах рассматриваемых подходов.

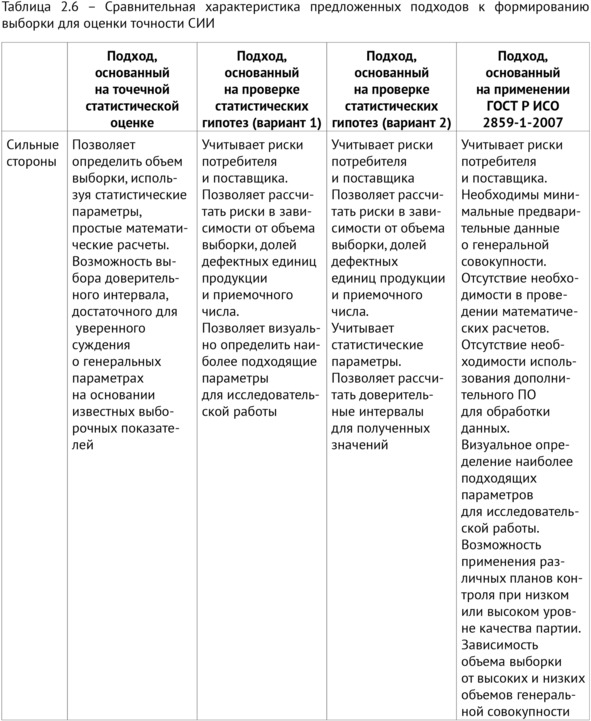
Таким образом, на данном этапе были разработаны несколько подходов для определения достаточной мощности НД для проведения мониторинга ПО с ТИИ. Использование точечной статистической оценки и подхода, основанного на проверке статистических гипотез, позволяет наиболее гибко рассчитать объемы выборки в зависимости от входных параметров проводимого исследования. Применение ГОСТ Р ИСО 2859-1-2007 для формирования выборки является приоритетным, если эксперимент затрагивает взаимодействие исследователя и сторонней организации; позволяет учитывать риски и ошибки для обеих сторон, вовлеченных в процесс.

Оптимальное количество исследований при проведении контроля качества работы изучаемых нами ТИИ для анализа медицинских изображений составляет 80 единиц. Это удовлетворяет требованиям репрезентативности, баланса рисков потребителя и поставщика услуг ТИИ, а также оптимизации трудозатрат сотрудников, вовлеченных в процесс контроля качества результатов работы ТИИ103.

2.3.3. Аналитический подход с использованием ROC-анализа (цитируется по оригинальной статье авторов104)

В ходе Московского эксперимента проведено исследование подходов к определению количества исследований, необходимых и достаточных для НД, который предназначен для проведения внешней валидации ИИ-сервисов (калибровочного тестирования) с учетом баланса классов «норма»/«патология»105.

Для этого использовались анонимизированные уникальные результаты 123 301 маммографии, полученные из ЕРИС ЕМИАС. Исследования классифицировались по наличию и отсутствию злокачественного новообразования (ЗНО) молочной железы. Анализировались выставленные значения по шкале Bi-RADS: 0 – в случае определения врачом 1-го или 2-го класса BI-RADS («норма») и 1 – в случае классов BI-RADS 3, 4, 5 («патология»). Изначально баланс классов составлял: «норма» – 89,3%/ «патология» – 10,7%.

Производилась оценка результатов работы СИИ, в качестве которого выступал один из сервисов искусственного интеллекта по направлению «маммография», участвующий в эксперименте. Валидация проходила в несколько этапов. На первом этапе данные были разделены на две группы – «норма» и «патология». Из разделенных данных случайным образом формировались выборки с балансом классов «норма»/«патология», содержащие «патологию» в количестве 50%, 40%, 30%, 20%, 10%. Минимальная выборка, сформированная случайным образом, содержала 30 исследований, далее размер выборки увеличивался с шагом 10, с учетом сохранения доли «патологии». Максимальный возможный объем изучаемой выборки составлял 26 386 (количество исследований с патологией, умноженное на 2) исследований и обусловлен ограничением вычислительных мощностей.

Для каждого баланса классов и объема случайным образом формировались подвыборки 10 000 раз с возвращением, для них рассчитывалась площадь под характеристической кривой (AUROC). По результатам работы CИИ рассчитаны средние значения AUROC для различных случайных наборов исследований с одинаковым балансом классов (рисунок 2.19).

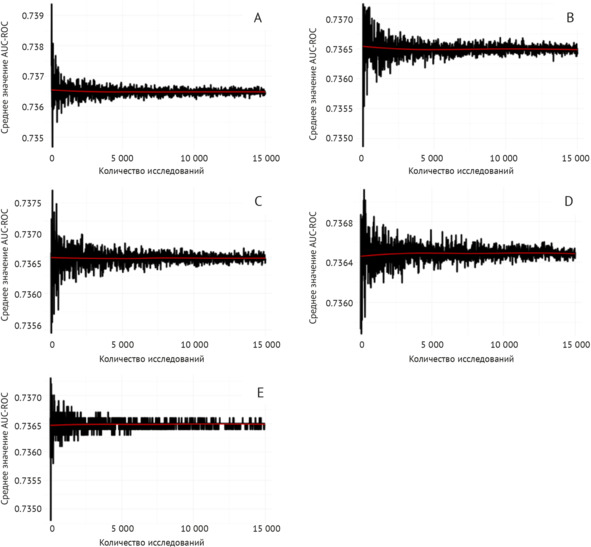
Рисунок 2.19 – Поведение средних значений AUROC для различных балансов классов «норма»/«патология». Красная линия показывает аппроксимирующую кривую. А – доля «патологии»» 10%; B – доля «патологии» 20%; C – доля «патологии» 30%; D – доля «патологии» 40%; E – доля «патологии» 50%

Следующим шагом средние значения AUCROC были подвергнуты трем типам анализа:

1. Фурье-анализ значений AUROC в зависимости от количества данных. Применение преобразования Фурье к колебаниям значений AUROC позволило выявить точку перехода, что является своеобразной границей между двумя различными распределениями. Эта граница соответствует значению 11 940 исследований. При использовании меньшего или равного количества исследований значения AUCROC для всех изученных долей «патологии» в балансе классов «норма»/«патология» распределяются по закону, близкому к распределению Коши. Причем если количество исследований превышало 11 940, то AUCROC имели нормальное распределение для 10% и 20% долей «патологии», логистическое – для 30% и 50% долей «патологии» и логарифмически нормальное – для 40% долей «патологии».

2. Анализ наиболее близкого теоретического распределения значений AUROC посредством применения информационных критериев Акаике и Байеса. Чтобы найти максимальное отклонение от линии тренда (рисунок 2.9) среднего показателя точности диагностики слева и справа от точки перехода (11 940 исследований), был определен ближайший тип простого распределения по минимуму критериев Акаике и Байеса. В таблице 2.7 представлены результаты сравнения распределения значений AUROC слева и справа от точки перехода для десяти различных распределений.

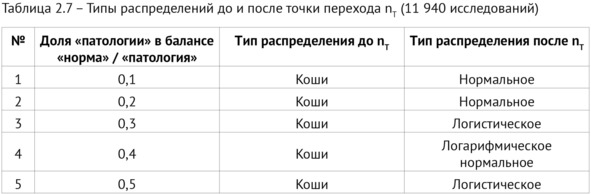
Из результатов анализа поведения аргумента спектральной функции AUROC и анализа ближайшего теоретического распределения следует, что до точки перехода для всех балансов классов сохраняется один и тот же тип распределения – распределение Коши. После точки перехода тип распределения меняется. Нормальное распределение наблюдается при 10% и 20% «патологии», логистическое – при 30% и 50% «патологии», а логнормальное распределение значений AUROC – при 40% «патологии».

3. Анализ коэффициента вариации в зависимости от количества исследований для установленного наиболее близкого типа распределения AUROC. Для оценки однородности значений AUROC был проведен анализ коэффициента вариации в зависимости от количества исследований (до 11 940 исследований). В случае распределения Коши коэффициент вариации рассчитывался по уравнению (2.5):

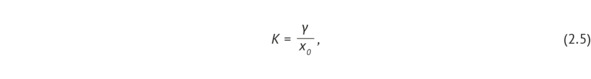
где Υ – масштабный параметр в распределении Коши; x0 – параметр сдвига в распределении Коши.

На рисунке 2.20 представлены результаты расчета зависимости коэффициента вариации распределения значений AUROC от количества исследований для пяти долей «патология» в балансе классов «норма»/«патология».

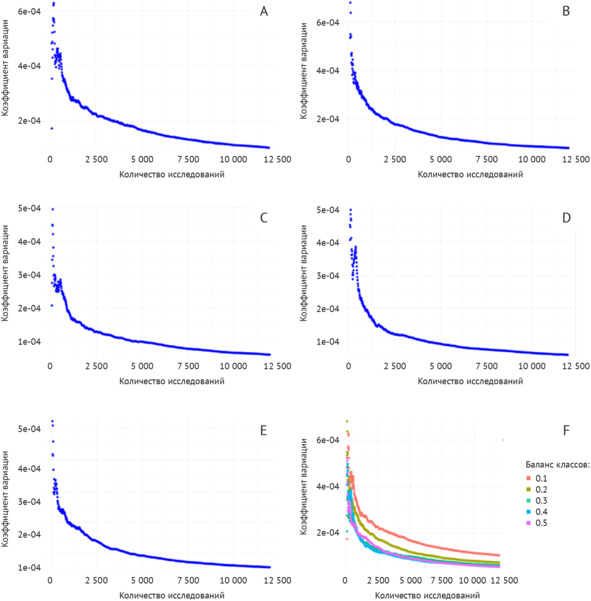
Рисунок 2.20 – Коэффициент вариации значений AUROC в зависимости от количества исследований для разных балансов классов. A – доля «патологии» 10%; B – доля «патологии» 20%; C – доля «патологии» 30%; D – доля «патологии» 40%; E – доля «патологии» 50%; F – обобщенное представление для всех долей «патологии»

Максимальное значение коэффициента вариации значений AUROC для 10% доли «патологии» достигается при количестве исследований, равном 190; для 20% доли – 80 исследований; для 30% доли – 120 исследований, для 40% доли – 110 исследований, а для 50% доли – 70 исследований.

Таким образом, была сформирована гипотеза о возможности следующего применения полученных результатов:

1. Определение AUROC на наборе данных с заданным балансом классов и соответствующим объемом выборки.

2. Определение доверительного интервала для AUROC с помощью метода бутстреппинга106.

3. Использование нижней границы доверительного интервала в качестве порогового значения для принятия решения о допуске СИИ AUROC.

Результаты, полученные с помощью данного подхода, сопоставимы с результатами одного из предыдущих подходов, описанных выше107. Частота встречаемости признака в популяции известна не всегда, может варьировать с течением времени и в разных популяциях, может быть очень низкой для редко встречающихся патологий. На основании вышеизложенного логичным решением является задавать баланс классов как постоянную величину и выбирать объем необходимых для валидации данных для заданного баланса классов.

Также следует отметить, что отклонение среднего значения AUROC от линии тренда с увеличением количества исследований уменьшается, что свидетельствует о том, что при использовании СИИ в клинической практике могут демонстрироваться показатели диагностической точности, отличные от полученных при валидационном тестировании. По этой причине на этапе валидации СИИ необходимо определить максимальные пределы изменения показателей диагностической точности и в дальнейшем проводить регулярный мониторинг его работы108.

2.3.4. Эмпирический подход с использованием ROC-анализа (цитируется по оригинальной статье авторов109)

Предложенный в 2023 г. оригинальный подход включает в себя поиск порогового значения размера выборки, минимального и достаточного для получения объективного значения AUROC, и рассматривает исследования с бинарной классификацией «норма»/«патология».

После разделения генеральной исходной выборки на подвыборки в соответствии с классами назначаются баланс классов k в диапазоне от 10 до 90% и размер выборки для тестирования ИИ-алгоритма n в диапазоне от 30 до 25 000 с шагом в 10. Вычисления первого этапа содержат две последовательные операции:

1. Для выбранной комбинации k и n из базовых подвыборок случайным образом отбирается по k × n исследований класса «патология» и (1 – k) × n исследований класса «норма». Операция повторяется 100 раз, в результате чего формируются 100 подвыборок размера n, в каждой из которых содержится k % исследований класса «патология», что соответствует 100-кратному повторению эксперимента для заданной комбинации n и k.

2. На каждой из 100 подвыборок проводятся тестирование ИИ-алгоритма и регистрация метрик – чувствительность (Se), специфичность (Sp) и AUROC. В результате выполнения расчетов получается матрица размером 100 × 3, т. е. по 100 значений каждой метрики, полученных на выборке размером n с долей патологических случаев k.

Действия по п. 1 и п. 2 повторяют для каждой из возможных комбинаций n и k.

Для практической апробации настоящего подхода были использованы результаты тестирования трех различных алгоритмов ИИ, участвующих в Московском эксперименте. Результаты расчета nкр были сопоставлены между тремя алгоритмами ИИ.

При разработке подхода были использованы следующие наборы данных (НД):

1. Результаты профилактической маммографии классифицировались по наличию («патология») и отсутствию («норма») признаков злокачественных новообразований молочной железы аналогично предыдущему описанному подходу:

1.1 НД, содержащий 143 710 исследований с результатами ИИ-алгоритма «А1», полученными за период с 01.02.2022 по 31.10.2022.

1.2 НД, содержащий 123 301 исследование с результатами работы ИИ-алгоритма «A2», полученными за период с 01.09.2021 по 27.12.2021.

2. Результаты рентгенографии органов грудной клетки классифицировались по наличию («патология») и отсутствию («норма») хотя бы одного из следующих признаков: плевральный выпот, пневмоторакс, очаг затемнения, инфильтрация, консолидация, диссеминация, полость, ателектаз, кальцинат, расширение средостения, кардиомегалия, нарушение целостности кортикального слоя. НД, содержащий 62 142 исследования с результатами работы ИИ-алгоритма «A3», полученными за период с 25.10.2023 по 21.11.2023.

Первично была проанализирована зависимость выборочных средних и медианных значений каждой из трех метрик AUROC, Se и Sp от доли патологических исследований в выборке. Для всех трех алгоритмов наблюдается совпадение этих значений (рисунок 2.21а). Общий вид зависимости упомянутых метрик, а также их дисперсии от размера выборки представлены на рисунке 2.21б на примере данных алгоритма A1. Зависимость для всех трех метрик имеет сходный вид симметричного затухающего колебания: с ростом n амплитуда разброса значений уменьшается, достигая некоторого условно стабильного диапазона. Вид зависимости дисперсии от n (рисунок 2.21б, нижний ряд) подтверждает целесообразность учета дисперсии подвыборок при сравнении средних. Согласно полученным данным, ожидаемое среднее значение AUROC для ИИ-алгоритмов А1 и А2 составляет 57%, и 70% для А3.

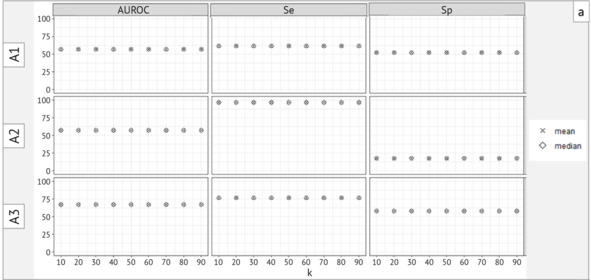
Рисунок 2.21а – Зависимость выборочных средних и медиан метрик ИИ-алгоритмов от k (а)

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

Указ Президента Российской Федерации от 10.10.2019 №490 «О развитии искусственного интеллекта в Российской Федерации».

2

Постановление Правительства Москвы от 21.11.2019 №1543-ПП «О проведении эксперимента по использованию инновационных технологий в области компьютерного зрения для анализа медицинских изображений и дальнейшего применения в системе здравоохранения города Москвы».

3

Там же.

4

Корсаков С. Н. Начертание нового способа исследования при помощи машин, сравнивающих идеи / пер. с франц.; под ред. А. С. Михайлова. М.: МИФИ, 2009. 44 c.

5

Владзимирский А. В. Институционализация научных исследований в области биотелеметрии в России/СССР: вторая половина XIX – ХХ вв.: дис. … д-ра истор. наук: 5.6.6 / Владзимирский Антон Вячеславович. М., 2023. 792 с.

6

Васильев Ю. А. Инновационные диагностические и организационные технологии в рентгенологии: дис. … д-ра мед. наук: 3.1.25; 3.3.9 / Васильев Юрий Александрович. М., 2024. 287 с.

7

Kim D. W., Jang H. Y., Kim K. W., et al. Design Characteristics of Studies Reporting the Performance of Artificial Intelligence Algorithms for Diagnostic Analysis of Medical Images: Results from Recently Published Papers // Korean J Radiol. 2019 Mar. Vol. 20, №3. Р. 405—410. https://doi.org/10.3348/kjr.2019.0025.

8

Nagendran M., Chen Y., Lovejoy C. A., al. Artificial intelligence versus clinicians: systematic review of design, reporting standards, and claims of deep learning studies // BMJ. 2020. №368. Р. m689. https://doi.org/10.1136/bmj.m689.