Философия и наука. От Анаксимандра до Коперника

Как видим, объяснение божественности светил дается Аристотелем в физике, поскольку в ней круговое движение, а также осуществляющие это движение простые тела наделяются статусом совершенства. Может сложиться впечатление, что Аристотель стремится подкрепить платоновское учение физикой. Но это предположение неверно. Метафизическое обоснование у Платона превратилось здесь только по имени в физическое обоснование, которое на деле остается сугубо философским. По своей сущности аргументы Платона и Аристотеля одни и те же. Душа, как воплощение принципа движения у Платона, у Аристотеля овеществляется в понятии простого тела. В качестве подтверждения нашей позиции приведём мнение Ю. Миттельштрасса, который пишет поэтому поводу, что «метафизическое обоснование, даваемое Аристотелем, только на нюанс отличается от обоснования Платона. Когда совершенные движения осуществляются не богами, а простыми телами, то только по имени место платоновской теологии занимает физика. Эта физика – составная часть общей онтологии, которая, как таковая, является у Аристотеля одновременно и теологией. Созвездия-боги Платона в физикалистской терминологии становятся просто телами, но эти тела движутся равномерно и кругообразно в силу тех же причин, что указываются Платоном: эта форма движения соответствует их сущности»28.

Что касается второго важнейшего компонента астрономии Аристотеля – теории гомоцентрических сфер и принципа статического геоцентризма, при том что теоретическое обоснование последнего является оригинальным вкладом Аристотеля в астрономическую концепцию сфер – то и он, так же как принцип «спасения явлений», находят обоснование в физике. Физика Аристотеля является целостным, законченным образованием, поэтому все ее положения так или иначе повлияли на астрономию. Тем не менее можно попытаться вычленить какое-то ядро, самые существенные идеи, которые оказались решающими для утверждения принцип астатического геоцентризма в астрономии.

Во-первых, Аристотель вводит в своей физике концепцию естественного движения и естественного места: любому телу, любой субстанции соответствует место, свойственное ему по природе. В этом месте тело пребывает неподвижно. Если же оно находится в месте, не свойственном ему по природе, то оно будет двигаться к месту, свойственному ему по природе. Например, если бросить ком земли вверх, то он будет падать вниз, т.е. двигаться к своему естественному месту. «Земле, как показывает наблюдение, по природе свойственно отовсюду двигаться к центру»». Естественным местом Земли является центр мира, «естественное движение частей и всей Земли, – пишет Аристотель, – направлено к центру Вселенной, именно поэтому Земля находится на самом деле в центре… центр Земли и Вселенной – один и тот же»29.

Во-вторых, Аристотель, как мы уже указывали, вводит в свою физику учение Эмпедокла о четырех первоэлементах (земле, воде, воздухе и огне) и дополняет его пятым элементом, из которого состоят все небесные тела, – эфиром. Все эти пять элементов, в соответствии с их тяжестью и инертностью, строго иерархически располагаются в пространстве – земля, вода, воздух, огонь, эфир. Земля, поскольку она самый тяжелый элемент, неподвижна и находится в самом низу, а так как мир сферичен, то низом будет центр, а верхом – периферия шара, т.е. земля опять-таки будет в центре мира.

Что же касается ее неподвижности, то Аристотель обосновывает ее с помощью следующих аргументов. Первый является чисто астрономическим. «Наблюдение показывает, что все [небесные тела], обладающие круговым движением, за исключением первой сферы, запаздывают и движутся несколькими движениями. Поэтому и Земля – движется ли она вокруг центра или находясь в центре – по необходимости должна двигаться двумя движениями. Если же это так, то должны происходить отклонения и попятные движения неподвижных звезд. Однако этого не наблюдается: одни и те же звезды всегда восходят и заходят в одних и тех же местах Земли»30.

Второй аргумент имеет физический характер и связан с аристотелевской концепцией движения. Аристотель пишет: «Что Земля по необходимости должна находиться в центре и быть неподвижной, очевидно… и потому, что тяжести, силой бросаемые вверх, падают снова на то же место отвесно, даже если сила забросит их на бесконечно большое расстояние»31. Если бы Земля двигалась, то такого не наблюдалось бы: брошенные вверх тела отставали бы, падали в точку, отстоящую в сторону, противоположную направлению движения Земли. Подобный аргумент неопровержим на базе аристотелевской физики, утверждающей тесную связь силы и движения и отрицающей движение тел по инерции. Именно поэтому вплоть до Галилея, в период господства аристотелевской физики, он оказался основным в деле утверждения статического геоцентризма. Для его опровержения была необходима иная физика – физика Галилея и Ньютона. Утверждение неподвижности и центрального положения Земли стало стержне образующим моментом аристотелевской и всей последующей астрономии. Характеризуя его, В. Ф. Асмус писал: «Земля неподвижно пребывает в центре мира. И в этом утверждении космология Аристотеля – шаг назад в сравнении с космологией Платона и пифагорейцев. И Платон, и пифагорейцы развивали учение о движении Земли… Со всей силой своего авторитета Аристотель положил на долгие времена конец зарождавшейся гелиоцентрической космологии»32.

Количество сфер в системе мира Аристотеля также было обусловлено физическими принципами: отрицанием пустоты и утверждением, что движение возможно только через взаимодействие. Евдокс и Каллипп использовали для описания движения светил систему, состоящую из нескольких сфер, но для каждого отдельного светила это был совершенно независимый механизм. Однако, если нет пустоты, то соседние системы сфер, определяющие движение каждого отдельного светила, соприкасаются, а если соприкасаются, то взаимодействуют, т.е. передают свое движение друг другу, и таким образом независимость движения каждого отдельного светила, по мнению Аристотеля, утрачивается. Независимость же светил друг от друга является чрезвычайно важным положением, поскольку установление любого приоритета приведёт к вычленению дополнительного, помимо Земли, центра. Чтобы сохранить независимость движения планет, Аристотель добавляет к каждой системе сфер дополнительные сферы, компенсирующие вращательный эффект первых, и называет их сферами, вращающимися в обратном направлении, или возвращающими.

В результате система мира Аристотеля выглядит следующим образом. Центром всех сфер является неподвижная Земля. Вокруг нее располагаются вложенные друг в друга сферы. Их порядок тот же, что и у Евдокса и Каллиппа: над Землёй идут сферы Луны, Солнца, Меркурия, Венеры, Марса, Юпитера, Сатурна и, наконец, сфера неподвижных звезд. Между системами сфер Сатурна и Юпитера, Юпитера и Марса Аристотель помещает по 3 компенсирующие сферы и по 4 сферы между каждыми другими системами сфер светил. Таким образом, в целом число различных сфер достигает 55.

Аристотелевское построение системы мира оказало решающее влияние на дальнейшее развитие астрономии. Введённый Аристотелем принцип статического геоцентризма предопределил все дальнейшее развитие астрономии и кардинально трансформировал принцип «спасения явлений». Если Евдокс понимал свой принцип чисто кинематический, а эта кинематика не нуждалась в физике, поскольку астрономия описывала движения разумных существ, то лишь потому, что Аристотель дал физическое обоснование движению созвездий, они попали в физическую сферу. Таким образом, созвездия, с одной стороны, оказались подвластными всеобщим законам движения, выразимым математически, а с другой – они были изъяты из произвольности математической гипотезы и допускали только улучшенную в аристотелевском смысле систему гомоцентрических сфер.

Эта аристотелевская система допускает только вращения вокруг осей, проходящих через центр мира. Очевидно, что здесь имеет место сужение применимости принципа «спасения явлений». Правда, и до Аристотеля полагали, что все движения осуществляются вокруг одного общего центра. Земля и воспринималась как такой общий центр, но то, что только она может быть центром, стало догматическим предписанием физики Аристотеля.

Подводя итог, хотим еще раз подчеркнуть, что астрономическая программа Аристотеля строилась на двух принципах: принципе спасения явлений и принципе статического геоцентризма. Причем первый из них являл собой программу математического объяснения и был увязан с принципом статического геоцентризма. Принцип статического геоцентризма стал метафизической частью общефилософской картины мира, а принцип спасения явлений – ее методом, эвристикой. Мир представал как система гомоцентрических сфер, в центре которых неподвижно покоится Земля, и задача астронома состояла в том, чтобы, основываясь на принципе кругового равномерного движения светил, математически описать эту систему так, чтобы в ней было сохранено видимое движение светил. В этой своей формулировке научная программа античной астрономии нашла у Аристотеля законченное выражение.

Как показало все дальнейшее развитие астрономии, соединение принципов геоцентризма и «спасения явлений» водной программе было противоречием, разрешить которое возможно было только отказавшись от статического геоцентризма. Но это означало выступать против авторитета Аристотеля в области метафизики и науки, против сложившихся канонов научного мышления. Поэтому оставалось ждать, когда это противоречие размоет само себя изнутри, вырастет до «чудовища», или когда сложатся философские условия возможности новой науки и нового мировоззрения. Возвращаясь же к Аристотелю, необходимо указать, что противоречие его астрономической программы сказалось сразу. Стало ясно, что теория гомоцентрических сфер не решает задач ни описательной, ни предсказательной астрономии, они необходимо терпели неудачу в воспроизведении видимого.

Глава 4.

Теория гомоцентрических сфер: аргументы «против»

Система гомоцентрических сфер не решала и не могла решить проблемы объяснения всей совокупности астрономических явлений. Уже во времена Евдокса и Аристотеля существовали эмпирические данные о том, что расстояния планет от Земли не остаются постоянными, а изменяются, в то время как в системе гомоцентрических сфер расстояние от некоторого светила до Земли с необходимостью предполагалось неизменным. Симпликий в «Комментарии» к аристотелевскому трактату «О Небе» указывал, что теории Евдоксовой школы не объясняли явления. Это относится не только к явлениям, открытым позднее, но и открытым ранее и известным ученикам Евдокса. «Я имею в виду тот факт, что иногда планеты появляются ближе к нам, а иногда дальше. Это очевидно для наших глаз в некоторых случаях. Так, Венера и Марс выглядят во много раз большими, когда они находятся в середине своего возвратного движения. В результате в безлунные ночи Венера позволяет телам отбрасывать тени»33.

Нельзя сказать, что неравенство в расстояниях относительно Земли каждого из этих тел не принималось во внимание учениками Евдокса. Так, Полемарх из Кизика (IV в. дон. э.), друг и ученик Евдокса, учитель Каллиппа, очевидно знал об этом. Но в конце концов он пренебрег этими явлениями, чтобы не отказываться от теории гомоцентрических сфер, которой отдавал предпочтение. Наконец, Автоликий Питанский, математик, современник Теофраста, первым попытался построить теорию, которая объясняла бы явления изменения расстояния светил от Земли, но ему, по свидетельству Сосигена, это не удалось.

П. Дюгем приводит мнение Сосигена, который, описывая явления, противоречащие гипотезе гомоцентрических сфер, упрекает сторонников этой гипотезы в том, что они не учитывают подобные факты: «Сферы сторонников Евдоксане объясняют наблюдаемые явления. Они не объясняют даже те, которые были известны еще до них и которые они сами рассматривали как истинные… По крайней мере, уже простое наблюдение обнаруживает одно явление, которое никому из них до Автоликия Питанского не удалось вывести из своих гипотез… Я имею в виду тот факт, что некоторые светила то удаляются, то находятся вблизи от нас»34.

Критические замечания, которые выдвинул Сосиген, сводятся к следующим. Теория гомоцентрических сфер неверна уже в самой своей основе. Из основного ее принципа вытекает, что каждое светило находится на постоянном расстоянии от Земли, но даже простое наблюдение показывает, что расстояния многих блуждающих светил от Земли меняются с течением времени. Они очевидны для Венеры и Марса, благодаря значительному изменению яркости этих планет. Они очевидны и для Луны, поскольку видимый диаметр этого светила может быть измерен, а измерение показывает, что он меняется в соотношении 12 к 11. Они становятся неоспоримыми благодаря тому факту, что центральные затмения Солнца оказываются то полными, то с остаточным венцом, что было бы невозможно, если бы расстояние от Луны до Солнца оставалось постоянным. Наконец, эти изменения расстояния вытекают из положений, признанных еще со времен Пифагора: если мы видим, что светило движется с переменной угловой скоростью, то это значит, что мы ведем наблюдения не из центра описываемой им окружности.

И тем не менее, все эти хорошо известные критические высказывания не привели к отказу от концепции космоса как системы гомоцентрических сфер. Казалось бы, простейший выход из создавшейся ситуации заключается в отказе от того, чтобы рассматривать Землю как необходимый центр мира и всех небесных движений, тем более что прецеденты подобного отказа уже существовали. Так, в это время ещё находила сторонников система Филолая, вводившего круговую орбиту суточного обращения Земли вокруг центрального огня. Его система предполагала, что расстояния от центрального огня до различных небесных светил остаются постоянными, но расстояния их до Земли изменяются, а потому систему Филолая можно было рассматривать как образец для возможного разрешения трудностей наблюдательной астрономии.

Мнения о движении Земли имели в общем и целом широкое хождение в Античности. Например, пифагореец Экфант считал, что Земля совершает суточное вращение вокруг своей оси, намеки на суточное движение Земли можно встретить и у Платона в «Тимее», это мнение отстаивал также и современник Аристотеля Гераклид Понтийский (388—315 гг. до н.э.), как о том свидетельствует Симпликий, и Гикетас Сиракузский, согласно Цицерону.

Однако лишь Аристарх Самосский (ок. 320—250 гг. до н.э.) предложил геокинетическую систему мира, в которой Земля вращалась не только вокруг своей оси, но и вокруг Солнца. Эта система получила широкую известность, и о ней мы знаем благодаря Архимеду (ок. 287—212 гг. до н.э.), изложившему основную идею Аристарха в своем сочинении «Исчисление песчинок», а также благодаря Плутарху. Характеризуя астрономическую систему Аристарха, Паннекук пишет: «Несомненно, что это была гелиоцентрическая система мира, однако без всякой детализации причин и следствий. Не давали этих деталей и поздние авторы, упоминавшие об Аристархе и его теории. Очевидно, она вообще не нашла приверженцев»35.

Существует, на наш взгляд, две причины, почему система Аристарха не была разработана, оставаясь лишь смелой, изобретательной, но не получившей широкого признания идеей. Первая причина заключается в общепринятое™ и общераспространенности принципов аристотелевской физики. Физическое обоснование принципа статического геоцентризма, его кажущаяся очевидность с точки зрения обыденного опыта и наличных физических представлений привели к тому, что геоцентрическая система мира стала рассматриваться как надежно обоснованная истина. Аристотелевская физика встала на пути всех иных астрономических идей и прежде всего газокинетических. Именно она стала позднее основой критики, выдвинутой против гелиоцентрических идей Птолемеем.

Второй причиной является оппозиция идее гелиоцентризма со стороны философов. Основу этой оппозиции составляли религиозно-философские соображения, согласно которым небесные движения являются сферой божественного. Свидетельства этой оппозиции мы находим у Плутархав его «Ликах на Луне» и у Сенеки в «Исследованиях о природе».

В силу этого астрономия была вынуждена искать обходные пути для решения трудностей, возникающих в связи с наблюдаемым движением светил. Однако сама проблема -противоречие системы гомоцентрических сфер и наблюдательной астрономии – была осознана. Поскольку она не могла быть решена в ситуации господства аристотелевской физики, то оставался один путь – разделить физику и астрономию, что и было сделано знаменитым стоиком и астрологом Посидонием (135—50 гг. до н.э.). Именно ему приписывается известное положение о различии между астрономической и физической науками: для астронома приемлемо любое объяснение, которое спасает явления, тогда как физик должен выводить истину исходя из первопричин. Астрономия пошла по пути создания различных хитроумных геометрических построений, позволяющих «спасать явления», не нарушая принципа геоцентризма.

Напомним, что теория гомоцентрических сфер натолкнулась на ряд трудностей при попытке сохранения видимого движения светил. К их числу относились следующие: во-первых, наблюдаемая неравномерность движения светил, которая свидетельствует о том, что наблюдение ведется не из центра их орбит; во-вторых, изменение яркости светил, которое также свидетельствует о том, что планеты изменяют своё расстояние от Земли; и, наконец, в-третьих, наблюдаемое попятное движение планет.

Решение этих проблем стало возможным только на путях математической астрономии. Еще в III в. до н. э. александрийский математик Аполлоний Пергский ввел понятие эксцентра – окружности, центр которой не совпадает с положением наблюдателя, находящегося на Земле.

Окружность АВСД (рис. 1) с центром в точке О изображает путь светила, Земля смещена относительно центра этой окружности. Светило движется по своей траектории равномерно, и только наблюдателю, находящемуся на Земле, движение светила предстает неравномерным: в точке А это движение предстает наиболее быстрым, а в точке С – наиболее медленным. По дуге АВС оно движется равнозамедленно, а по дуге СДА равноускоренно. Эксцентр 3 объясняет изменение яркости светил: в А они более яркие, чем в С. Кроме того, на рис. 1 видно, что светило пройдет дуги АВ и ДА за меньшее время, чем дуги ВС и СД. В случае, если этим светилом будет Солнце, этот факт и объяснит неравенство сезонов.

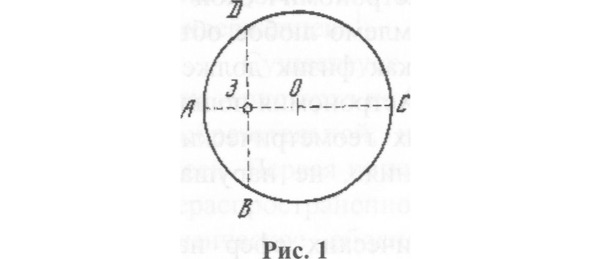
Конструкция Аполлония объясняла часть наблюдаемых неравномерностей за исключением попятного движения планет и была заимствована в астрономию Гиппархом (190—125 гг. до н.э.), крупнейшим астрономом Древней Греции и всего доптолемеевского периода, труды которого не сохранились, нор об основных идеях которого известно от Птолемея.

Глава 5.

Математическая астрономия: эксцентры и эпициклы. От Птолемея к Проклу

Клавдий Птолемей (ок. 90 – ок. 168 гг.), крупнейший греческий математик, принимает аристотелевский принцип геоцентризма и обоснование этого принципа на основании аристотелевской физики. Однако принцип «спасения явлений» понимает как чисто математическую задачу.

В том, что все движения должны быть круговыми, Птолемей согласен со всей предшествующей традицией. Он лишь молчаливо опускает аристотелевское требование одного-единого центра для всех движений. Поскольку для математика, по Птолемею, конечная цель должна заключаться в доказательстве того, что все планеты осуществляют равномерные круговые движения, а такое движение сохраняется и при принятии эксцентров, эпициклов и экванта, то простые гомоцентрические сферы уступают у Птолемея место множеству круговых движений вокруг различных центров.

Для объяснения неравномерности движения светил и изменения их яркости Птолемей использовал конструкцию, геометрически эквивалентную эксцентру, но с помощью которой можно было объяснить также и попятное движение светил. Она основывается на введении эпициклов, идея которых также принадлежит Аполлонию Пергскому.

Согласно этой конструкции, Земля находится в центре большой окружности, называемой деферентом, по которой равномерно движется точка S, являющаяся центром второй, меньшей окружности, называемой эпициклом (рис. 2).

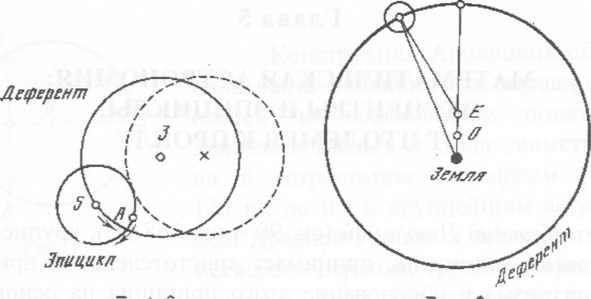
Рис. 2 Рис. 3

По эпициклу движется светило. Если периоды обращения по деференту и эпициклу равны между собой, то в результате сложения обоих движений светило движется вокруг Земли по окружности, обозначенной на рис. 2 штриховой линией, которая есть не что иное, как эксцентр. Однако в модели Птолемея ни деференты, ни эпициклы не были тождественны Аполлониевым. У Аполлония деференты представляли собой окружность, Птолемей же, указав, что невозможно объяснить наблюдаемые движения планет с помощью равномерного движения их эпициклов по деферентам, ввел понятие экванта, или уравнивающей точки. Как видно на рис. 3, Земля помещалась на некотором расстоянии от центра окружности О. С противоположной стороны на том же расстоянии от центра, что и Земля, находилась точка Е, называемая эквантом. Движение центра эпицикла по деференту определялось следующим условием – оно должно было казаться равномерным, если смотреть на него из экванта. Для наблюдателя, находящегося на Земле или в центре окружности О, движение уже не было равномерным. Теперь для согласования теоретически предсказываемого движения планеты с данными наблюдения надлежало соответствующим образом подобрать положение центра деферента, а тем самым и экванта.

С помощью столь хитроумного математического построения Птолемей сумел искусно обыграть принцип равномерного кругового движения – движение якобы равномерное было, по сути, неравномерным, и в результате центр эпицикла двигался по деференту с переменной скоростью. Таким образом, с помощью системы круговых равномерных движений воспроизводилось видимое неравномерное движение светил.

Отметим, что, однако, введение экванта было нарушением аксиомы равномерного кругового движения: согласно этой аксиоме движение светила должно быть равномерным по отношению к центру круга, а не к экванту. Это нарушение оказывало постоянное возмущающее воздействие на имманентное развитие астрономической теории.

Второй проблемой была проблема объяснения попятных и колебательных движений планет. Для объяснения этих явлений Птолемей также использовал механизм эпициклов. Но если при объяснении наблюдаемого неравномерного движения Солнца периоды обращения по эпициклу и деференту равны между собой, то периоды обращения планет по эпициклам, используемым для объяснения попятного движения планет, когда они вычерчивают на небе петлю, независимы от периодов обращения центров эпициклов по деферентам.

Попятное движение наблюдается у так называемых верхних планет – Марса, Юпитера и Сатурна. Они перемещаются на фоне звезд с запада на восток, т.е. совершают прямое движение, однако за некоторое время до противостояния они останавливаются, а затем начинают отступать, передвигаясь в обратном направлении с востока на запад, совершая таким образом попятное движение. Затем, после противостояния, они вновь останавливаются и вновь совершают прямое движение, описав таким образом на небосводе петлю.

Для объяснения этого явления Птолемей ввел следующую схему: центр эпицикла каждой верхней планеты движется с собственной скоростью, отличной от скоростей центров эпициклов других планет, а период обращения по эпициклу одинаков для всех верхних планет и составляет год. В результате наложения этих двух движений и появляется наблюдаемая петля. Механизм возникновения петли можно изобразить графически следующим образом (рис. 4).

На рис. 4 видно, что когда центр эпицикла находится в точке Ei, планета занимает положение Рь а когда центр эпицикла перемещается в точку Е2, планета занимает положение Р2. При перемещении из Pi в Р2 планета описывает петлю, проекцию которой на сфере звезд мы и видим.

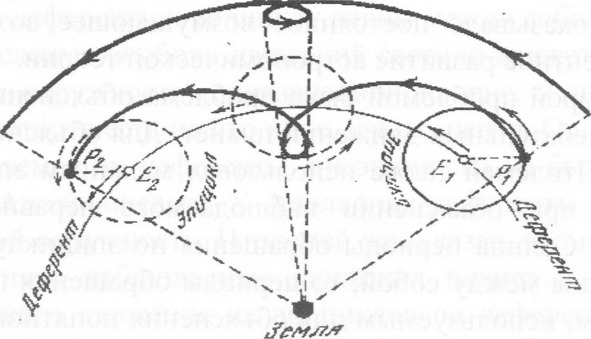
Рис. 4

Колебательное движение наблюдается у нижних планет – Венеры и Меркурия – и совершается относительно Солнца. Если начать наблюдение за Венерой, когда она появляется на горизонте в пору вечерних сумерек в западной части неба и продолжать это наблюдение, то можно увидеть, что в последующие дни Венера будет все более отклоняться к востоку и все дольше оставаться на небосклоне пока, наконец, ее заход не произойдет на три часа позже захода Солнца. Затем она начинает медленно возвращаться обратно, пока не исчезнет в лучах Солнца, а через некоторое время она появляется на востоке перед самым восходом Солнца, т.е. она его миновала и теперь расположена западнее. Дальнейшие наблюдения покажут, что она восходит все раньше и раньше, пока не достигнет крайней восточной точки, опередив восход Солнца на три часа. Затем она снова начинает отступать к Солнцу, двигаясь к западу.