
Полная версия
От микроорганизмов до мегаполисов. Поиск компромисса между прогрессом и будущим планеты
В начале Нового времени развитие научных методов исследований и изобретение и применение новых, мощных математических и аналитических инструментов (математического анализа в середине XVII века, успехов в области теоретической физики и химии и основ современной экономики и демографии в течение XIX века) позволили анализировать рост в чисто количественной форме и использовать релевантные формулы роста для прогноза долгосрочных траекторий изучаемых феноменов. Роберт Мальтус (1766–1834), один из основоположников демографических и экономических исследований, вызвал серьезную обеспокоенность своими выводами, в которых противопоставлялся линейный рост средств к существованию и экспоненциальный рост населения (Malthus, 1798).
В отличие от Мальтуса, Пьер Франсуа Ферхюльст (1804–1849), бельгийский математик, сегодня известен только историкам науки, статистикам, демографам и биологам. Но через четыре десятка лет после публикации работы Мальтуса Ферхюльст внес существенный вклад в наше понимание роста, опубликовав первые реалистичные формулы, разработанные специально для того, чтобы выразить развитие ограниченного роста (Verhulst, 1838; 1845; 1847). Подобный рост управляет не только развитием всех организмов, но и повышением производительности новых методов организации труда, распространением множества инноваций и внедрением множества потребительских продуктов. Прежде чем начать раскрывать тему феноменов роста и их траекторий (в главе 2), я предложу краткое, но вполне исчерпывающее введение в характер этих формальных моделей роста и соответствующих им кривых.
Линейный и экспоненциальный рост
Это две распространенные, но совершенно различные формы роста, траектории которых отражают простые равенства. «Относительно медленный и устойчивый» будет лучшим качественным описанием линейного роста, а «ускоряющийся и переходящий в стремительный» – экспоненциального. Все, что подчиняется линейному росту, возрастает на одну ту же величину в течение заданного периода времени, следовательно, формула линейного роста выглядит просто:
Nt = N0 + kt,
где новое значение величины Nt (в момент времени t) рассчитывается путем увеличения начального значения (N0) на постоянную величину k за период времени t.
Анализ большого числа сталагмитов показывает, что эти конусообразные колонны солей кальция, образующиеся на полу пещер благодаря капающей воде, часто растут тысячелетиями почти линейно (White and Culver, 2012). Даже сравнительно быстрый рост со скоростью 0,1 мм в год означает, что сталагмит высотой 1 м вырастет за тысячу лет всего на 10 см (1000 мм + 1000 × 0,1). Если нанести этот результат на график, мы увидим плавно восходящую линию (рис. 1.3). Это, конечно, означает, что темп роста как доля общей высоты сталагмита будет постоянно снижаться. Для сталагмита, растущего со скоростью 0,1 мм в год в течение 1000 лет, он будет составлять 0,01 % в течение первого года, но всего 0,009 % спустя тысячелетие.
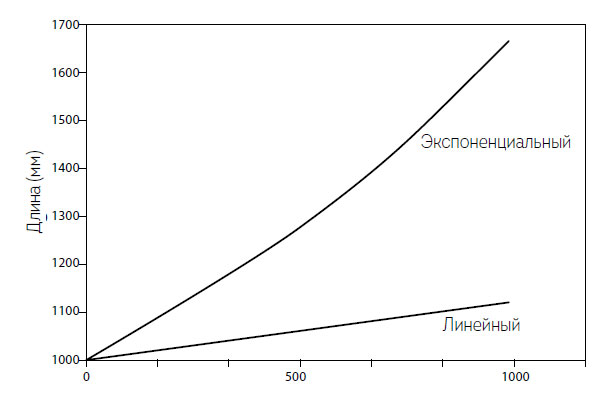
Рис. 1.3. Тысячелетие прироста сталагмитов, иллюстрирующее траектории линейного и экспоненциального роста
Для сравнения во всех случаях экспоненциального роста значение увеличивается в одинаковое число раз за каждый одинаковый период времени. Основной функциональной зависимостью является
Nt = N0 (1 + r)t,
где r – скорость роста, выраженная как доля единицы роста на единицу времени, например, при росте 7 % на единицу времени r = 0,07.
Экспоненциальный рост также можно выразить – после простой поправки на выбор единиц измерения времени – как
Nt = N0ert,
где e (e = 2,7183, основа натурального логарифма) возводится в степень rt, что легко проделать с помощью любого научного калькулятора. Мы можем представить себе пещеру, где количество капающей воды, содержащей одинаковую долю растворенных солей, постоянно возрастает, ведя к экспоненциальному росту сталагмита.
Если предположить очень малый прирост длины в размере 0,05 % в год, то сталагмит за 1000 лет увеличился бы в длину почти на 65 см (1,000 мм × 2,7180,0005 × 1000 = 1648,6 мм общей длины, или прирост в размере 64,86 см), что почти на 50 % больше, чем при линейном росте. Экспоненциальный рост отображается в виде восходящей кривой, крутизна подъема которой определяется скоростью роста (рис. 1.3). Через 10 000 лет линейно растущий сталагмит удвоил бы свою высоту, и она достигла бы 2 м, в то время как экспоненциально растущему сталагмиту понадобилась бы гигантская пещера, так как его высота составила бы 148,3 м. Экспонента – произведение скорости роста и времени, поэтому прирост может быть одинаково большим как в случае низкого прироста на более длинных интервалах времени, так и в случае более коротких интервалов более быстрого роста.
Еще одно простое сравнение показывает, что траектории линейного и экспоненциального роста находятся близко друг к другу на самых ранних стадиях роста, когда значения скорости роста и временного интервала невелики по сравнению с единицей: вскоре они начинают расходиться и в конце концов оказываются далеко друг от друга. Голд (Gold, 1992) считал, что колонии бактерий, живущих глубоко под землей, заполняют до 1 % всего пористого пространства в верхних 5 км земной коры, в то время как, по мнению Уитмана и др. (Whitman et al., 1998), объем, занимаемый микроорганизмами, составляет всего 0,016 % пористого пространства. Это все равно означает огромную совокупную массу микроорганизмов, но с крайне низким темпом размножения. Давайте предположим (ради простого примера), что физические и химические ограничения позволяют крошечной колонии, состоящей из 100 клеток (внезапно оказавшейся в результате сейсмического явления в новой полости скальной породы), расти на пять клеток в час. Очевидно, что к концу первого часа клеток будет 105, через 10 часов такого линейного роста колония достигнет 150 клеток, а через 50 и 100 часов – 350 и 600 соответственно.
По сравнению со многими обычными бактериями, Mycobacterium tuberculosis (микобактерия туберкулеза) – служившая одной из самых частых причин преждевременной смерти во времена до изобретения антибиотиков и по-прежнему остающаяся одной из основных причин смертности инфекционного генезиса, а также являющаяся причиной одной из наиболее устойчивых форм инфекционных заболеваний (Gillespie, 2002) – в большинстве обстоятельств размножается в легких человека медленно. Но в благоприятных лабораторных условиях количество ее клеток удваивается в течение 15 часов, то есть со скоростью приблизительно 5 % в час. Если мы снова начнем со 100 клеток, то к концу первого часа получим 105 – то же самое, что и при линейном росте подземных микроорганизмов. Через 10 часов экспоненциального роста в колонии будет 165 клеток (всего на 10 % больше, чем при линейном росте), но через 50 часов результат экспоненциального роста составит 1218 клеток (приблизительно в 3,5 раза больше, чем в случае линейного) и 14 841 клетку через 100 часов, то есть почти в 25 раз больше. Контраст очевиден: без априорных знаний по истечении первого часа мы не смогли бы определить разницу, но через 100 часов разница становится огромной, так как экспоненциальный рост на порядок выше.
Случаи линейного (постоянного) роста широко распространены. Расстояние (длина), которое проходит свет, излучаемый мириадами звезд, увеличивается на 300 000 000 м (299 792 458 м, если говорить точно) каждую секунду. Расстояние, преодолеваемое грузовиком, движущимся в среднем со скоростью 100 км/ч по ночному шоссе, за то же время возрастает на 27,7 м. Согласно закону Ома – напряжение (вольты, V) равно силе тока (амперы, А), умноженной на сопротивление (ом, Ω) электрической цепи, – когда сопротивление не меняется, с ростом напряжения значение силы тока в цепи растет линейно[3]. Фиксированная (и не облагаемая налогами) почасовая оплата дает линейное увеличение зарплаты при увеличении рабочего времени. Поминутная тарификация сотовой связи (а не безлимитный тариф) ведет к линейному увеличению ежемесячного счета при линейном увеличении продолжительности разговоров.
В природе линейный рост часто встречается в качестве временного на ранних этапах постнатального развития, будь то поросята или дети. В развитых странах уже более века средняя ожидаемая продолжительность жизни растет линейно. Линейная траектория – единственная долгосрочная траектория роста урожаев, от основных зерновых до фруктов. Совершенствование технических характеристик и возможностей машин также происходит линейно, включая рост средней мощности американских легковых автомобилей со времен Ford Model T в 1908 году, максимальную силу тяги и степень двухконтурности[4] реактивных двигателей с момента их появления, максимальную скорость поездов, давление в котлах паровозов (с начала регулярной эксплуатации в 1830 году) и максимальное водоизмещение кораблей.
Иногда простой линейный рост является результатом сложных взаимодействий. В период между 1945 и 1978 годами потребление бензина в США представляло собой почти идеальный линейный рост, и после короткого четырехлетнего периода спада в 1983 году он возобновился и продолжался до 2007 года (USEIA, 2017b). Две линейные траектории стали результатом взаимного влияния нелинейных изменений, таких как резкий рост, более чем в семь раз в период с 1945 по 2015 год, числа владельцев автомобилей и застой в средней эффективности потребления топлива автомобильными двигателями до 1977 года, последующего значительного повышения с 1978 по 1985 год и нового застоя на следующие 25 лет (USEPA, 2015).
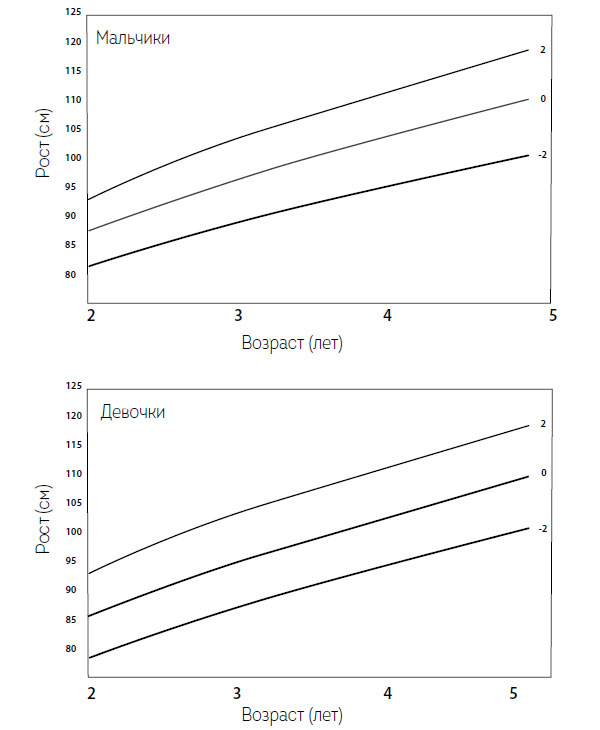
Рис. 1.4. Графики предполагаемого увеличения роста в зависимости от возраста (средние значения и величины в рамках двух стандартных отклонений) для мальчиков и девочек двух – пяти лет. Упрощено по данным ВОЗ (2006)
Некоторые организмы, включая бактерии, выращиваемые в лабораториях, и маленьких детей, испытывают периоды линейного роста, прибавляя то же число клеток или рост или массу в течение конкретных периодов времени. Бактерии развиваются этим путем, когда обеспечены ограниченным, но постоянным количеством питательных веществ. У детей наблюдаются периоды линейного увеличения как веса, так и роста. Например, американские мальчики испытывают краткие периоды линейной прибавки веса в возрасте между 21 и 36 месяцами (Kuczmarski et al., 2002), и Нормы развития детей Всемирной организации здравоохранения (ВОЗ) указывают на идеальное линейное увеличение роста у мальчиков в возрасте от трех до пяти лет и почти линейную траекторию у девочек того же возраста (WHO, 2006; рис. 1.4).
Экспоненциальный ростЭкспоненциальный рост, начинающийся постепенно и затем резко возрастающий, приковывает внимание. Свойства этого роста, прежде известные как геометрический коэффициент или геометрическая прогрессия, иллюстрируются сотни лет, пожалуй, даже тысячи, хотя первый письменный пример относится к 1256 году – это история об изобретателе шахмат, который попросил своего правителя-благодетеля вознаградить его, удваивая число зерен риса (или пшеницы?) на каждой следующей клетке поля. 128 зерен (27) в конце первого ряда – заурядное число, однако к концу среднего, четвертого, ряда оно достигло 2,1 млрд (231), а в конце последнего – около 9,2 квинтиллиона (9,2 × 1018) зерен.
Основной характеристикой экспоненциального роста является его стремительность, когда каждое новое увеличение значительно превосходит предыдущее: прибавки в последнем ряду шахматной доски в 256 раз больше, чем общее число, накопленное в конце предпоследнего, и составляет 99,61 % всех добавленных зерен. Очевидно, нежелательный экспоненциальный рост можно остановить – с тем или иным трудом – на ранних этапах, но по мере продолжения роста задача может быстро стать нерешаемой. Если предположить, что средняя масса рисового зернышка составляет 25 мг, их общее число (которое очевидно не сможет поместиться на шахматной доске) будет равняться 230 гигатоннам риса, что почти в 500 раз больше ежегодного мирового урожая, составившего в 2015 году немногим менее 500 мегатонн.
За длительные периоды даже ничтожная скорость роста даст невероятные результаты. Применять интервалы космического масштаба нет нужды – достаточно отсылки к Древнему миру. Когда Римская империя достигла своего апогея (во II веке н. э.), ей было необходимо собирать 12 Мт зерна (большая часть которого выращивалась в Египте и отправлялась в Италию), чтобы прокормить население размером около 60 млн человек (Garnsey, 1988; Erdkamp, 2005; Smil, 2010c). Если представить себе, что Римская империя существовала бы и по сегодняшний день, ее урожай зерна рос бы на 0,5 % в год и к 2015 году достиг бы 160 Гт, что более чем в 60 раз больше реально собранного в 2015 году мирового урожая зерна в размере 2,5 Гт, с помощью которого накормили 7 млрд человек.
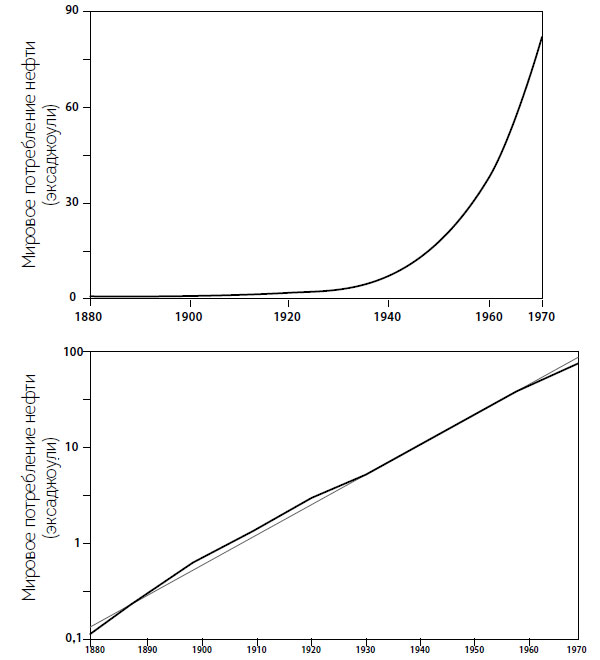
Рис. 1.5. Годовой мировой рост потребления необработанной нефти, 1880–1970-е: экспоненциальный рост, отображенный на линейной и полулогарифмической шкале. По данным (Smil, 2017b
Линейная шкала плохо подходит для отображения экспоненциального роста, полная траектория которого часто охватывает величины в несколько порядков. Если попытаться вместить все значения на линейной оси y, их будет невозможно разобрать кроме самых больших порядков, и результатом всегда будет J-образная кривая с почти линейной частью сравнительно медленного прироста, за которым следует более или менее крутой подъем. Если же нанести значения постоянного экспоненциального роста на график в полулогарифмических координатах (с линейной осью x для времени и логарифмической осью у для растущего количественного значения), то можно получить идеально прямую линию, и значения будут легко читаться на оси y, даже когда рост охватывает значения нескольких порядков. Таким образом, составление графика в полулогарифмическом масштабе – простой способ определить, является ли некий набор данных результатом экспоненциального роста. На рис. 1.5 сравниваются два графика для подобного феномена: на нем отображается рост одной из основ современной цивилизации, почти идеально экспоненциальный рост мирового потребления нефти в период между 1880 и 1970 годами.
Коммерческое производство топлива началось в ничтожном масштабе всего в трех странах: России (с 1846 года), Канаде (с 1858 года) и США (с 1859 года). К 1875 году его объем составлял всего около 2 Мт, но с ростом добычи в США и России и выходом на рынок новых производителей (Румынии, Индонезии, Бирмы, Ирана) производство стало расти экспоненциально и к 1930 году достигло около 170 Мт. В результате экономического кризиса 1930-х годов в отрасли произошло короткое замедление, но ее экспоненциальный рост возобновился в 1945 году, и благодаря обнаружению гигантских месторождений на Ближнем Востоке и в России к середине 1970-х добыча возросла на три порядка (немногим больше чем в 1000 раз) за последние 100 лет.
Периоды экспоненциального роста встречаются и в современной экономике. Подобные явления характерны, в частности, для роста валового продукта в таких быстро развивающихся странах, как Япония, Южная Корея и Китай, после 1985 года. Они были связаны с объемом годовых продаж потребительской электроники, массовый спрос на которую создал новые глобальные рынки. На привлекательности временного экспоненциального роста воображаемых доходов строятся мошеннические инвестиционные схемы (пирамиды Понци): на ранних этапах развития таких моделей экспоненциальный рост можно остановить контролируемым образом, но внезапный коллапс роста, характерный для таких схем, всегда имеет нежелательные последствия. Развитие технического прогресса также часто бывает отмечено явными периодами экспоненциального роста, но впервые экспоненциальный рост (и его опасности) стал активно обсуждаться публикой в связи с ростом населения (Malthus, 1798).
Знаменитая работа «Очерк закона о народонаселении» Томаса Роберта Мальтуса напоминает труды Леонарда Эйлера, ведущего ученого XVIII века, покинувшего Швейцарию ради работы в России и Пруссии (Bacaër, 2011). В Берлине, после возвращения из России, Эйлер опубликовал – на латыни, в то время по-прежнему считавшейся стандартом языка научных работ, – «Введение в анализ бесконечно малых [величин]» (Euler, 1748). Одна из рассматриваемых в этой книге проблем связана с проходившей в 1747 году в Берлине переписью населения, в которой приняли участие 100 000 человек. Эйлер хотел узнать, каким будет население, растущее ежегодно на одну тридцатую (3,33 % в год), через 100 лет. Его ответ, полученный с помощью логарифмов, гласил, что оно вырастет более чем в 25 раз: поскольку Pn = P0(1 + r)n, результат за 100 лет составит 100 000 × (1 + 1/30)100, или 2 654 874. Затем Эйлер продемонстрировал, как рассчитывать годовой прирост населения и периоды удвоения.
Но именно Мальтус сделал вопрос экспоненциального роста основным для таких новых дисциплин, как демография и политэкономия. Его основной вывод о том, что «потенциал населения определенно больше потенциала земли, производящей пропитание для человека», так как безудержный рост населения будет происходить экспоненциально, а рост средств к существованию – линейно (Malthus 1798, 8), получил широкое хождение:
Если взять любой размер населения Земли, например, тысячу миллионов, количество людей будет увеличиваться по модели 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 и т. д., а пропитание – по модели 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и т. д. Через два века с четвертью соотношение населения и средств пропитания будет 512 к 10, через три века – 4096 к 13, а через две тысячи лет разница будет почти неисчислимой, хотя сельскохозяйственная продукция к тому времени возрастет в огромной степени.
Чарльз Дарвин иллюстрировал процесс, ссылаясь на Мальтуса и Линнея и собственные расчеты последствий безудержного размножения слонов (Darwin, 1861, 63):
Не существует исключения из правила, что каждое органическое существо размножается с такой скоростью, что если не уничтожать его, то Земля вскоре покроется потомством одной пары. Даже число медленно размножающихся людей удвоилось за двадцать пять лет, и при такой скорости через несколько тысяч лет от их потомков будет не протолкнуться. Линней подсчитал, что если однолетнее растение дает всего два семени – а таких непродуктивных растений не существует – и выросшие из них растения снова дадут два семени и так далее, то через двадцать лет этих растений будет миллион. Слоны считаются самыми медленно размножающимися из животных, и мне было нелегко оценить вероятную минимальную скорость их естественного прироста: предположим, что они начинают размножаться в возрасте тридцати лет и продолжают до девяноста, производя на свет в этот период три пары детенышей. Если это так, то к концу пятого века будет существовать 5 млн слонов, являющихся потомками первой пары.
Как я объясню подробнее в главах, посвященных росту организмов и артефактов, эти расчеты нужно воспринимать с правильной долей внимания и скепсиса, но у них есть два общих фундаментальных свойства. Во-первых, в отличие от линейного роста, где абсолютный прирост на единицу времени не меняется, экспоненциальный рост ведет к увеличению абсолютной прибавки на единицу времени по мере расширения базы. Экономика США росла на 5,5 % в 1957-м, а также в 1970 году, но во втором случае абсолютный прирост был в 2,27 раза больше – $56 млрд по сравнению с $24,7 млрд (FRED, 2017). В большинстве распространенных случаев экспоненциального роста его скорость не является идеально постоянной: она или немного опережает график, или колеблется в пределах среднего значения за длительный период.
Немного сокращающаяся скорость роста даст менее ярко выраженный рост. Десятилетние значения роста ВВП США с 1970 года представляют хороший пример: они сократились с 9,5 % в течение 1970-х до 7,7 % в течение 1980-х годов, 5,3 % в течение 1990-х и до всего 4 % в течение первого десятилетия XXI века (FRED, 2017). Возрастающая скорость роста приведет к суперэкспоненциальному темпу роста: годовой темп составил 8,6 % в течение первых пяти лет, 9,8 % – в период между 2001 и 2005 годами и 11,3 % между 2006 и 2010 годами (NBS, 2016). Колеблющийся темп роста является нормой для развития экономики в долгосрочной перспективе: например, экономический рост США (выраженный в ВВП) во второй половине XX века составлял в среднем 7 % в год, но это сложное среднее значение изменений скрывает значительные годовые колебания, достигавшие таких крайних значений, как 0,3 % в 1954 году (единственный год сокращения ВВП) и 13 % в 1978 году (FRED, 2017).
Во-вторых, экспоненциальный рост, природный или антропогенный, всегда является лишь временным феноменом, заканчивающимся в результате разнообразных физических, экологических, экономических или социальных ограничений. Ядерная цепная реакция обязательно завершается (в связи с ограниченной массой расщепляющегося материала), как и схемы (пирамиды инвестиций) Понци (когда приток новых денежных средств опускается ниже выплат). Но финансовые пирамиды могут существовать довольно долго: вспомните аферу Бернарда Мейдоффа – настолько продуманную схему Понци, что надзорные органы, неоднократно (хотя определенно не настолько тщательно, как следовало) проверявшие его компанию, более 30 лет не могли ни к чему прицепиться. Мейдофф получил обманным путем около $65 млрд от инвесторов, прежде чем его пирамида рухнула в результате крупнейшего со времен окончания Второй мировой войны экономического кризиса осенью 2008 года (Ross, 2016).
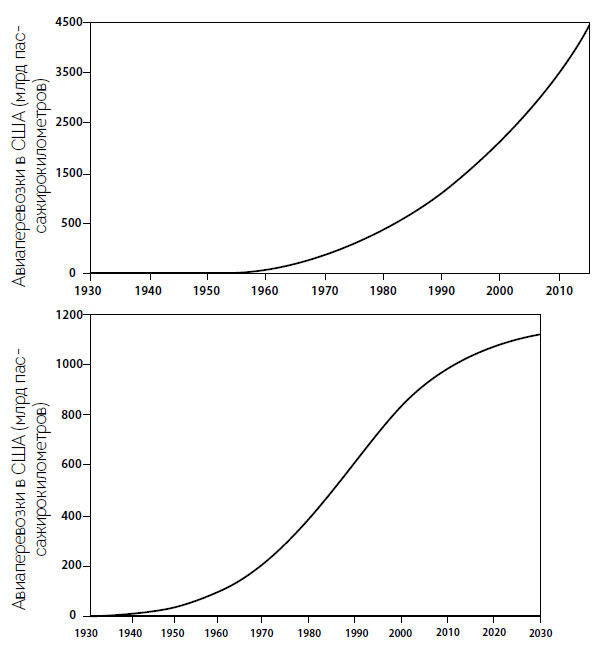
Рис. 1.6. Прогнозы роста авиаперевозок в США (в миллиардах пассажирокилометров) на основе данных за 1930–1980 годы (сверху, больше всего подходит регрессия четвертого порядка) и за 1930–2015 годы (снизу, больше всего подходит логистическая кривая с точкой перегиба в 1987 году). Данные из различных годовых отчетов Международной организации гражданской авиации
Вот почему долгосрочное прогнозирование на основе экспоненциального роста может оказаться некорректным. Эту мысль можно проиллюстрировать с помощью множества примеров, основанных на реальных историях, и я выбрал историю впечатляющего роста пассажиропотока авиакомпаний в США после 1950 года. В течение 1950-х годовой экспоненциальный рост составлял в среднем 11,1 %, а в 1960-х и 1970-х соответственно 12,4 и 9,4 %. График годовых показателей пассажирокилометров всех американских авиалиний в период между 1930 и 1980 годами представляет собой траекторию, почти идеально соответствующую регрессии четвертого порядка (полиномиальному уравнению четвертого порядка, где r2 = 0,9998), и при продолжении этой модели роста показатели 1980 года к 2015 году выросли бы почти в 10 раз (рис. 1.6).
В реальности же пассажиропоток американских авиалиний пошел по траектории сокращения роста (в первом десятилетии XXI века средний годовой рост составил всего 0,9 %), а полный цикл с 1930 по 2015 год хорошо вписывается в логистическую (симметричную) кривую с четырьмя параметрами, где значение 2015 года всего в 2,3 раза выше по сравнению с 1980 годом, и дальнейший ограниченный прирост ожидается только к 2030 году (рис. 1.6). Принимать временные высокие темпы ежегодного экспоненциального роста за индикаторы будущего долгосрочного развития – фундаментальная ошибка, а также стойкая привычка, особенно свойственная тем, кто продвигает новые устройства, разработки или практики: они берут темпы роста на ранних стадиях, которые часто бывают впечатляющими, и используют их, чтобы спрогнозировать неизбежное господство развивающегося феномена.
Эту ошибку можно проиллюстрировать с помощью множества свежих примеров, и я выбрал пример роста мощности ветряных турбин Vestas, установок, ведущих к сдвигу в сторону декарбонизации глобального производства электричества. Этот датский производитель начал продавать машины мощностью 55 кВт в 1981 году, к 1989 году у него была турбина мощностью 225 кВт, в 1995 году была представлена машина мощностью 600 кВт, а в 1999 году появилась турбина мощностью 2 МВт. Наиболее подходящая кривая для траектории этого быстрого роста за последние двадцать лет XX века (логистическая кривая с пятью параметрами, где R2 = 0,978) спрогнозировала бы к 2005 году модели турбин с мощностью почти 10 МВт и свыше 100 МВт к 2015 году. Но в 2018 году самый мощный агрегат Vestas для установки на суше производил всего 4,2 МВт, а самый большой, предназначенный для морских ветряных электростанций, – 8 МВт с возможностью увеличения до 9 МВт (Vestas, 2017a), а появление агрегата мощностью 100 МВт стало крайне маловероятным. Этот пример отрезвляющего контраста между быстрым ростом на ранних этапах развития технических инноваций и последующим неизбежным формированием сигмоидальных (S-образных) кривых стоит вспоминать каждый раз, когда вы слышите в новостях о том, что к 2025 году все машины будут электрическими или что к 2030 году появятся новые батареи с впечатляюще высокой энергоемкостью.









